基于核Fisher判别分析的高职学生考试成绩预测

杨东海+胡凌+钱莹

摘 要：高职教育中对学生考试成绩的预测，可以帮助教师提前评估教学效果，优化课程设计，从而提高学生考试成绩和教学质量。文章基于核Fisher判别分析，搭建了高职学生期末考试成绩预测模型，以学生自身特点和平时表现等构成模型输入变量的维度信息，来预测学生是否可以通过期末考试。实验中以深圳信息职业技术学院学生作为研究分析对象，考察建立模型的预测精度，并与经典算法进行了比较。实验结果证明，核Fisher判别分析具有良好的泛化能力，其预测精度与支持向量机相近，但优于C4.5决策树方法。

关键词：核Fisher判别分析；高职教育；考试成绩预测

中图分类号： TP391 文献标志码：A 文章编号：1673-8454（2016）16-0076-04

一、引言

随着国家“十三五”规划的顺利进行，加快发展职业教育已经越来越成为国家、社会和教育界的共识，高职院校不可避免的成为了培养实用技能型人才的主要基地。随着高职招生人数的不断扩大，以及社会还没有摆脱对职业教育的传统观念，高职院校的生源质量每况愈下。一部分学生的基础知识较差，学习新知识的意愿不强，无论在课堂上与老师的互动，还是课下的平时作业完成情况，都不尽如人意，使得教师很难在真正考试之前评估教学效果，从而造成教学质量下降。因此，如何提高高职学生的学习成绩，成为社会和学校都关注的问题。在教学过程中、期末考试之前，有针对性的建立模型预测考试成绩，提前评估教学效果，可以起到预警的作用。对那些有可能不及格的学生及时纠正其不良学习行为，并进行单独辅导，则有助于提高学生成绩，减少不合格现象，进而提高学生培养质量，优化课程设计，促进教师教学进步。

正是意识到学生成绩预测对提高教学质量、促进教学改革的重要性，国内一些学者在几年前就已经开始对该领域展开研究。大部分学者将成绩预测视为分类问题，于是多采用数据挖掘或机器学习领域的算法，如决策树、人工神经网络、支持向量机等来建立模型。其中，决策树方法因为理论发展成熟、易于理解等优点，被广泛用于大学生英语成绩预测[1]、大学生计算机等级考试成绩预测[2]、一般性课程的成绩预测[3， 4]等；而人工神经网络和支持向量机也因为扎实的理论基础和广泛应用，被用于大学生课程成绩预测[5，6]，并取得良好的效果。

核Fisher判别分析作为基于核函数的机器学习算法的典型代表[7]，其分类效果在其他模式识别和预测领域得到了很好的验证[8，9]。学者们前期的研究成果表明，决策树、神经网络和支持向量机方法在学生考试成绩预测方面均取得了不俗的成绩。但是到目前为止，我们尚未发现有学者应用完整的核Fisher判别分析进行大学生成绩预测的系统报道（虽然有学者利用线性Fisher判别分析对SVM模型中的数据因素进行加权[6]）。因此，本文提出利用核Fisher判别分析作为工具，尝试寻找学生学习属性与成绩之间隐含的非线性复杂关系，从而建立高职在校学生期末考试成绩预测模型。实验分析中以深圳信息职业技术学院物流管理专业2015级3个班级的学生作为研究对象，采用学生性别、生源地、考勤表现和平时作业成绩等作为模型的输入变量，来预测学生的期末考试成绩。实验结果证明，核Fisher判别分析的泛化能力强，其预测精度与支持向量机十分接近，并且优于C4.5决策树方法。

二、核Fisher判别分析

核Fisher判别分析[7]是基于核函数的机器学习算法中的一种，其结合了线性Fisher判别分析与核函数的思想，能够有效地解决现实中的分类问题[8， 9] 。

1.线性Fisher判别分析原理[10]

线性Fisher判别分析是一种有监督学习的分类方法。给定一组d维空间的样本数据x∈R（i∈1，2，.....n），n为样本数据集的大小，他们分别属于不同的两类，则样本类别标识记为yi∈{1，2}。属于类1的n1个样本记为X1={x11，x12，......x1}，属于类2的n2个样本记为X2={x21，x22，......x2}。算法“学习”或者“训练”的过程，就是要找到样本数据与其类别隐含的内在关系模式x→y。线性Fisher判别分析构造学习模型的核心目标是寻找一个d维向量w∈R，当样本数据向该方向投影时，最大化类间散度和类内散度的比值，使得样本数据在这个方向上尽可能的分开，达到清楚辨识的目的。定义某一类样本（i=1，2）数据类内均值为：

2.核Fisher判别分析原理

线性Fisher判别分析是一种线性分类器，当样本数据与类别呈现线性关系时其分类效果会很好。但是实际问题中，样本数据与其类别的关系往往呈现出复杂的非线性，则线性Fisher判别分析的分类效果就会差强人意，而且也无法解决模式识别中常见的维数灾难问题。在支持向量机中成功应用的核函数的出现解决了这个问题[11， 12]。核函数首先将数据从低维的输入向量空间R映射到高维（甚至是无限维）的特征空间，即φ：R→。通过某些核φ（·），映射可表示为xi→φ（xi）=（a1φ1（xi），……，amφm（xi），……）。在这个高维的特征空间中应用线性Fisher判别分析，在特征空间得到的线性分类器通过核映射回原始的输入数据空间R时，就得到了非线性分类器。

基于线性Fisher判别分析的原理，核Fisher判别分析在特征空间要寻找w∈，使得下式F（w）最大化：

三、实验及分析

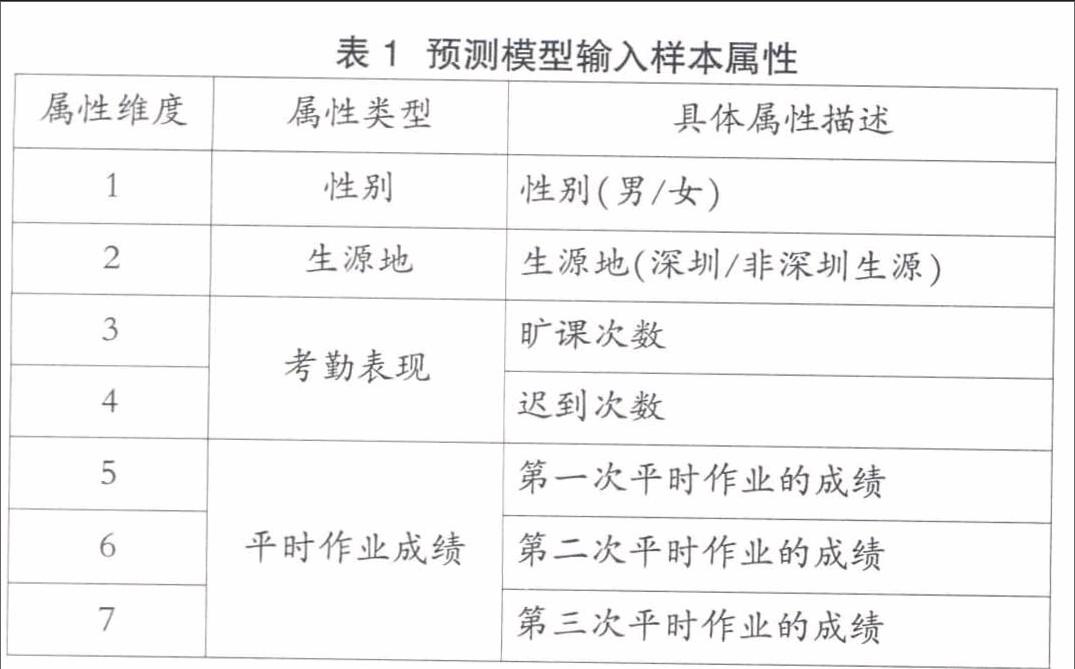
为了评估本文提出的基于核Fisher判别分析的预测模型的实际效果，我们将深圳信息职业技术学院物流管理专业2015级3个班级共151名学生作为研究对象，收集第一学年某门专业基础课的期末考试成绩及相关因素作为模型的输出和输入变量。预测模型的输入变量（样本属性）应该与考试成绩密切相关，我们选择输入向量时主要根据日常教学经验反馈的以下几点事实：①大学生个体的期末成绩往往与其旷课、迟到次数（出勤反映学习态度）负相关，与平时作业成绩（平时作业代表学习态度和对知识的理解程度）正相关；②本专业学生的自有特点是女同学平均成绩比男同学略胜一筹；③深圳市外生源较市内生源入学平均成绩高。因此，我们选择学生的性别、生源地、出勤表现和平时作业成绩作为样本的属性变量，具体总结如表1所示。

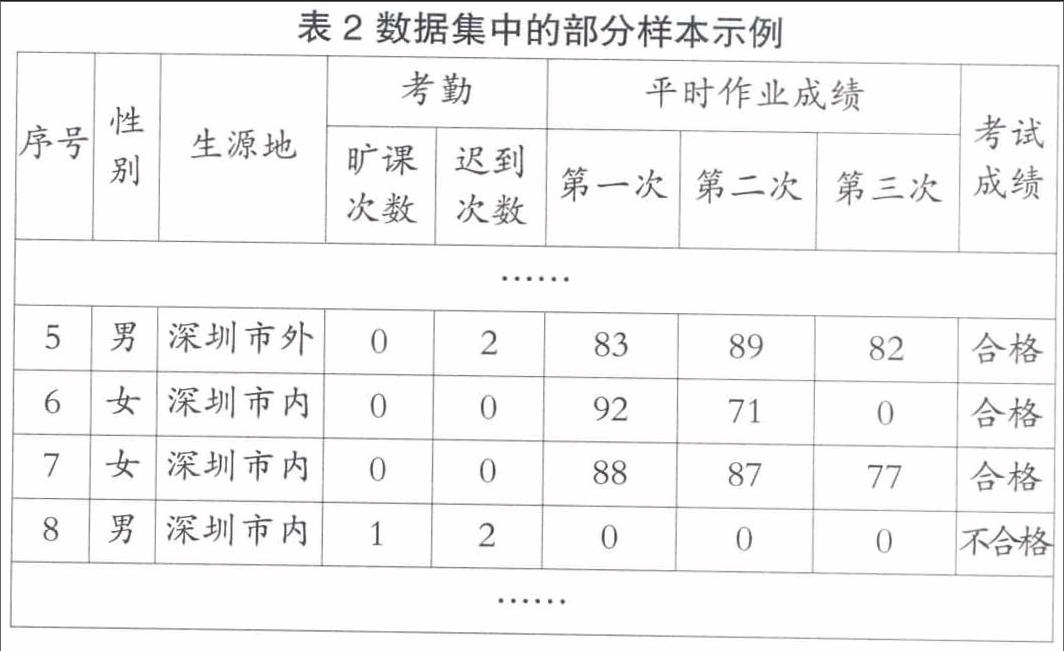
此外，将所有学生分为两类，期末考试成绩大于等于60分记为“合格”，否则记为“不合格”。数据集中的部分样本示例如表2所示。

我们在MATLAB环境中编写核Fisher判别分析的实现代码，并装载收集到的原始数据集进行实验研究。为了比较核Fisher判别分析对高职学生成绩的预测效果，我们还测试了支持向量机SVM算法和C4.5决策树方法，这两种方法同样在MATLAB环境中实现。在核Fisher判别分析和SVM建模时，为了防止样本中某个维度的数值过大而在核函数计算中淹没其他维度数据的作用，我们先对原始数据进行预处理，即将原始数据标准化在[-1，+1]的范围内。在使用C4.5决策树建模时，因为其能够同时处理连续值和离散值的属性，训练和测试过程不受数据大小的影响，所以C4.5方法实现中仍旧保持原始数据，不进行额外处理。

由于实验用的原始数据集较小，如果简单地分为训练和测试两个数据集合，评估效果容易出现偏差。为了能够全面反映各种算法预测的精度，我们对整个样本数据进行多次划分，每次从全体数据集中选择10%的数据作为测试数据，其余数据用于训练模型和确定最优参数。此外，核Fisher判别分析和SVM均采用RBF径向基核K（xi，xj）=exp（-γ||xi-xj||2）作为核函数，其中γ是核参数。由于训练得到的模型的泛化能力高度依赖于核函数参数、正则化参数或惩罚系数的选择，因此选择最优的参数很有必要。在实验中，核Fisher判别分析的正则化参数设为δ=10-3，核Fisher判别分析和SVM中用到的核参数γ和惩罚系数由10-交叉验证网格搜索法来确定[13]。在最优参数设置下对测试样本数据进行预测，每次测试的准确率定义如下：

准确率=×100%（14）

实验的结果是进行十次测试的平均值，如表3所示。

从实验结果可以看出，基于核函数方法的核Fisher判别分析和SVM预测精度相近（其中核Fisher判别分析预测准确度的平均值略微高于SVM），这一点与两者在标准数据集上的测试结果一致[7]，但是两者的预测精度都明显高于C4.5决策树算法。C4.5决策树方法训练模型时，主要采用信息增益率作为选择根结点和各内部结点中分支属性的评价标准，训练速度快，得到的模型直观性强，规则易于被使用者理解。但是决策树方法在训练集上的预测效果往往优于测试集，即容易出现过拟合的现象。核Fisher判别分析和SVM利用的核函数将数据从低维的输入空间映射到高维的特征空间，在特征空间都基于各自的分类原理构建线性分类器使得两类数据集尽可能的分开，得到的线性分类器经过核函数映射回输入空间后，即成为非线性分类器。因此，核Fisher判别分析和SVM得到的预测模型泛化性能良好，能够挖掘出输入样本属性与其类别之间隐含的非线性复杂关系。另外，本文用到的原始实验数据采集自学生的实际情况，其中包含着一部分不完全、有噪声的数据，比如有些学生学习能力强、成绩突出，但是有个别作业没有提交或是迟到的情况，却依然会通过考试。噪声数据会使得决策树方法产生的过拟合现象更加严重，减小了泛化能力，从而影响测试效果。与之对应的是，核Fisher判别分析和SVM分类的基本原理保证了尽可能将噪声数据的影响降到最低，所以会取得较好的预测效果。

四、结束语

在我国的长期规划中，高等职业教育受到越来越多的重视。基于目前高职教学和生源的自有特点，建立准确的学生考试成绩预测模型，能够帮助教师提前评估教学成果，改进教学方法，对提高教学质量具有非常重要的意义。本文在MATLAB环境中建立了基于核Fisher判别方法的学生考试成绩预测模型，可以在期末考试之前，根据学生的自身特点和平时表现来预测其成绩。在以本校高职学生为研究对象的实验中，核Fisher判别方法取得了良好的预测效果，可以成为一线教师提高教学的有力工具。同时，只要能够正确地选择输入变量的属性，该模型可以被直接推广到一般本科院校的学生考试成绩预测中，同时也为后续建立教育信息化决策系统打下基础。

在后续的研究中，可以在两个方面进行进一步的拓展。第一，在实际情况中，经常会出现通过考试的学生数量远远超过未通过考试的学生数量，使得不同类别的原始采样数据数量不平衡，这有可能影响模型的泛化能力。未来可以考虑如何针对不平衡数据集进行训练和测试。第二，本文建立的分类模型，仅仅可以根据输入向量来预测学生是否通过考试，而不能预测学生具体的考试分数。期望以后能够应用基于核函数的回归分析算法[11]，进行学生成绩的分数预测。

参考文献：

[1]孙力，程玉霞.大数据时代网络教育学习成绩预测的研究与实现——以本科公共课程统考英语为例[J]. 开放教育研究，2015（3）： 74-80.

[2]黄振功.决策树在高校计算机等级考试成绩分析的应用[J].科技资讯，2013（25）：18-19.

[3]武彤，王秀坤.决策树算法在学生成绩预测分析中的应用[J].微计算机信息，2010（3）： 209-211.

[4]于立红，张建伟.基于数据挖掘的高职生成绩分析与预测[J].郑州轻工业学院学报，2006（3）： 77-79.

[5]邱文教.基于人工神经网络的学习成绩预测[J].计算机与信息技术，2010（4）： 5-6.

[6]李建萍.基于加权支持向量机的学习成绩预测模型[J].中国科教创新导刊，2009（14）： 137-138.

[7]Mika S， R tsch G， Weston J， et al. Fisher discriminant analysis with kernels[C]. Neural Networks for Signal Processing IX， 1999. Proceedings of the 1999 IEEE Signal Processing Society Workshop.

[8]李建云，邱菀华.核Fisher判别分析方法评估消费者信用风险[J].系统工程理论方法应用，2004（6）： 548-552.

[9]李映，焦李成.基于核Fisher判别分析的目标识别[J].西安电子科技大学学报， 2003（2）：179-182.

[10]Bishop C.Pattern Recognition and Machine Learning[M]. Springer Science & Business Media， 2006.

[11]Vapnik V.The nature of statistical learning theory[M]. Springer Science & Business Media， 2013.

[12]Mercer J. Functions of positive and negative type， and their connection with the theory of integral equations[J]. Philosophical transactions of the royal society of London. Series A， containing papers of a mathematical or physical character，1909， 209： 415-446.

[13]Chang C， Lin C. LIBSVM： a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology （TIST），2011， 2（3）： 27.

（编辑：鲁利瑞）