一种改进型光纤陀螺惯导系统单轴旋转调制方案

岳栋栋，蔡春龙

（北京航天时代光电科技有限公司，北京100094）

一种改进型光纤陀螺惯导系统单轴旋转调制方案

岳栋栋，蔡春龙

（北京航天时代光电科技有限公司，北京100094）

在常规单轴两位置旋转调制方案基础上，提出了一种改进型光纤陀螺惯导系统单轴旋转调制方案，该方案深入研究了载体航向角变化时，通过优选惯性测量组合（IMU）的旋转停止位置，实现了比常规调制方案更好的导航误差自补偿效果。通过理论推导和仿真验证，证明了本方案的有效性、可行性。

惯导系统；旋转调制；光纤陀螺；单轴旋转方案

0 引言

由于惯性导航系统存在误差随时间积累、制造成本较高、对工业基础要求较高等不足之处［1］，加上现在许多领域对惯导系统的精度要求也在不断提高，单纯从提高惯性仪表精度来提高惯导系统的精度变得越来越困难，成本也越来越高。旋转调制技术是一种从系统角度提高惯导系统精度的方法，该技术将惯性导航系统放置在旋转机构上，利用其旋转运动来调制陀螺和加速度计的常值漂移等相关误差在导航解算中的传递形式，使其在导航解算中呈现周期（或近似周期）的形式并通过积分作用而抵消或抑制，从而达到系统误差的自补偿效果。由于光学陀螺与加速度有关的误差项几乎可忽略不计，因此旋转调制技术是提高光学陀螺惯导系统导航精度的一种有效技术手段。旋转调制技术在国外长航时高精度光学陀螺惯导系统中已得到实用且应用效果显著，例如Sperry公司的MK39MOD3C型捷联惯导系统（SINS），通过单轴旋转调制技术将SINS的精度由1n mile/8h提高到1n mile/24h，适用于舰艇等需要长时间自主导航的应用领域［2-3］。

现有单轴旋转调制式惯导系统的转位方案大都不隔离载体的航向运动，即控制惯性组合（IMU）相对于载体坐标系而非地理坐标系以一定的旋转方式转动，这时载体的航向角变化（拐弯）将会影响旋转调制系统对水平方向惯性仪表误差的自补偿效果。例如在极端情况下，若载体的航向角速度刚好和IMU旋转调制的角速度大小相等、方向相反，则从地理坐标系看来，IMU完全没有转动，自然在此时间段内就不会有旋转调制误差自补偿效果［4］。针对这个问题，本文分析了载体航向角变化对系统误差的影响，并提出了一种改进型单轴旋转调制方案，可以有效降低载体航向运动对旋转调制效果的影响，从而相应提高系统的导航精度。

1 旋转调制型惯导系统导航算法概述

旋转调制式惯导系统一般是在传统捷联惯导系统的外面加上旋转机构和测角装置，其导航解算仍采用捷联惯导算法［5］。惯性元件输出的是IMU相对于惯性空间的角速度和加速度，其算法原理就是根据姿态更新矩阵、初始对准信息和加速度计输出，可由导航计算机实时解算出载体的速度和位置参数，但直接算出的姿态参数是IMU的姿态，还需根据测角装置测出的IMU相对于载体的旋转角度才能解调出载体姿态信息。其基本原理如图1所示，s系指IMU坐标系，n系指导航坐标系。

图1　旋转调制型捷联惯性导航系统原理图Fig.1 Schematic of rotation modulation SINS

式中，ωsis即为陀螺仪的输出。

对旋转调制型捷联惯导系统进行误差分析，可得姿态误差方程以及速度误差方程的矢量形式，分别为:

2 改进型单轴旋转调制方案

2.1常规两位置转/停方案介绍

旋转调制方案关系到惯导系统的导航精度、整体结构和成本，选取合适的旋转方案十分重要。IMU的单向连续转动会引入旋转轴方向上的陀螺仪标度因数误差与地球自转角速度天向分量以及旋转角速度的耦合项，该耦合项会引起随时间积累的天向姿态角误差［6］，所以单轴旋转调制方案大都采取正/反转的形式，同时从缩短旋转机构工作时间以降低故障率的角度出发，旋转方案一般要采取“转/停”工作方式。

常规的单轴两位置转/停方案及次序如图2所示，各旋转次序说明如下:

次序1:从A点出发以角速度ω绕转轴正转180°到达位置B，并在B点停止Ts秒；

次序2:从B点出发以角速度ω绕转轴正转180°到达位置A，并在A点停止Ts秒；

次序3:从A点出发以角速度ω绕转轴反转180°到达位置B，并在B点停止Ts秒；

次序4:从B点出发以角速度ω绕转轴反转180°到达位置A，并在A点停止Ts秒。

以上4次转动为1个旋转调制周期T，并据此循环转动。

图2　常规单轴两位置转/停方案Fig.2 Scheme of common single axis two positions rotation

旋转调制型捷联惯导系统的姿态误差方程如式（4）所示，当载体的航向角不发生变化时，可得惯导系统在1个旋转周期（即T=4Tr+4Ts，转动时间内，由陀螺常值零偏引起的姿态误差角在导航坐标系下的表达式为:

可见，在1个完整的旋转周期内，该方案可以完全抵消水平惯性仪表常值漂移引起的导航误差，不能消除旋转轴向惯性仪表常值漂移引起的导航误差。式（6）成立的条件是载体方位不发生变化，但实际中当载体转弯使其方位发生变化时，水平方向陀螺的零偏误差就不能完全抵消。

2.2改进型单轴旋转调制方案介绍

旋转调制自补偿的目标就是要在1个旋转周期T内使被调制陀螺常值漂移的积分为零，只要满足这个条件，不需要IMU必须在每一个对称位置停留也能完成陀螺常值漂移的自动补偿。针对常规单轴两位置转/停方案的不足，在载体转弯情况下，考虑能否不改变旋转方式和停止时间，只改变IMU停留的位置来尽可能消除因水平陀螺常值漂移未完全自补偿而引起的姿态误差。针对此问题，本文提出了改进型单轴旋转调制方案，如图3所示，每一个调制周期包括如下8个旋转次序:

次序1:从A点出发以角速度ω绕转轴正转180°到达位置B；

次序2:在B点停止Ts秒；

次序3:从B点出发以角速度ω绕转轴正转θ1到位置C；

次序4:在C点停止Ts秒；

次序5:从C点出发以角速度ω绕转轴反转180°到达位置D；

次序6:在D点停止Ts秒；

次序7:从D点出发以角速度ω绕转轴反转θ2到位置E；

次序8:在E点停止Ts秒。

E点也就是下个转动周期的起始位置A点。以上8次转动为1个旋转调制周期，并据此循环转动。

图3　改进型单轴旋转调制方案Fig.3 Scheme of new single axis rotation modulation

为了便于分析问题，按以上8个次序将1个完整的旋转调制过程划分为8个过程，画出IMU在1个旋转调制周期内的旋转角速度示意图，如图4所示。

图4　改进方案一个调制周期内旋转角速度示意图Fig.4 IMU's rotation rate in a period of new scheme

2.3改进型单轴旋转调制方案实现

惯性导航系统解算得t时刻IMU坐标系相对于导航坐标系的航向角为ψ（t）:

过程1由陀螺常值漂移引起的水平方向姿态误差角为:

式中，ψk1表示过程1中每个导航周期解算得到的IMU相对于导航坐标系的航向角。

同理可得其余过程中，由陀螺常值漂移引起的水平方向姿态误差角为:

式中，ψki表示过程i中每个导航周期解算得到的IMU相对于导航坐标系的航向角。

在本调制周期过程2结束时，优选出本调制周期过程4的停止位置，计算出来θ1，给单轴转位机构发送相应的位置指令。假设本调制周期过程3、过程4时，载体的方位没有发生变化，则过程4中IMU相对于导航坐标系的航向角ψ4等于过程2结束时刻导航系统解算出的IMU相对于导航坐标系的航向角ψ2加上IMU在过程3中的转动角度θ1。

上周期过程7结束后，根据式（9）可以得到φE7、φN7，由于在上周期选取过程8的停止位置时假设ψ6=ψ8，但是实际过程中不一定满足这个式子，这样会存在实际过程与计算过程的自补偿残差δE1、δN1。

本调制周期过程4抵消的是本调制周期内过程2中陀螺常值漂移在导航坐标系内的积分以及上调制周期内过程5与过程7的自补偿残差，上调制周期内实际过程8与计算过程8的自补偿残差δE1、δN1。使陀螺常值漂移的积分引起的水平姿态误差角满足式（12）、式（13）即可:

当εx=εy=ε时，由式（12）求得:

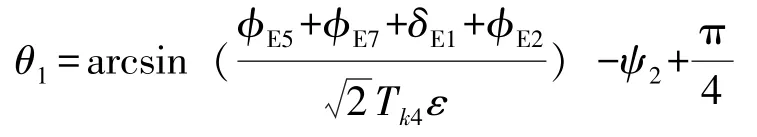
由式（13）求得:

式（12）和式（13）解不一定相同，当两式解不相同时，求使水平姿态角绝对值之和φ最小的θ1来选取过程4的停止位置。

在本调制周期过程6结束时，优选出本调制周期过程8的停止位置，计算出来θ2，给单轴转位机构发送相应的位置指令。假设在本调制周期过程7、过程8时，载体的方位没有发生变化，则过程8中IMU相对于导航坐标系的航向角ψ8等于过程6结束时刻导航系统解算出的IMU相对于导航坐标系的航向角ψ6加上IMU在过程7中的转动角度θ2。

本调制周期过程4结束时，根据式（9）可以得到φE4、φN4，由于在本周期选取过程4的停止位置时假设ψ2=ψ4，但是实际过程中不一定满足这个式子，这样会存在实际过程4与计算过程4的自补偿残差δE2、δN2。

过程8抵消的是本调制周期内过程6中陀螺常值漂移在导航坐标系的积分、本调制周期内过程1与过程3的自补偿残差以及本调制周期内实际过程4与计算过程4的自补偿残差δE2，δN2。使陀螺常值漂移的积分引起的水平姿态误差角满足式（16）、式（17）即可:

由式（16）求得:

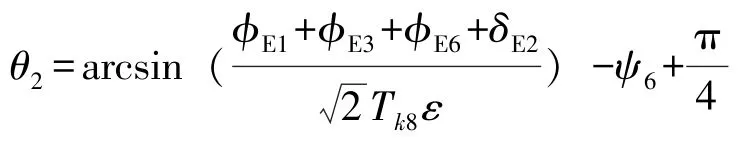
由式（17）求得:

式（16）和式（17）解不一定相同，当两式解不相同时，求使水平姿态角绝对值之和φ最小的θ2来选取过程8的停止位置。

本改进方案不需要事先知道载体的转弯速度、转弯角度等参数，利用惯导系统解算出来的信息来优选IMU停止位置，方案具有可行性；并且对载体的转弯过程没有要求，不要求载体方位变化遵循固定的规律，方案具有实用价值。

3 仿真验证

3.1仿真条件设置

这里对常规单轴两位置转/停方案和改进型的单轴旋转方案进行仿真研究和对比分析。导航坐标系选为东北天地理坐标系，载体坐标系为右前上坐标系，仿真步长为0.005s，初始时刻载体3个姿态角均为0°，初始时刻载体所处的位置为北纬40.06899°，东经116.24558°，载体行驶速度为:vby=100m/s，vbx=vbz=0。只考虑两水平陀螺的常值零偏为0.1（°）/h，不考虑其他误差。仿真过程中，IMU在每个位置停止时间为2min，IMU的旋转角速度为6（°）/s［7］。

3.2仿真结果分析

在3.1节的条件下，进行了不同转弯角度和不同转弯速度下的多组仿真，载体转弯后，保持直线运行，每次仿真进行1h，仿真结果如表1所示。

表1　不同条件时两种方案导航位置误差仿真结果比较Table 1 Position errors of two scheme on different conditions

从表1可以看出，载体以不同的转弯速度完成不同程度的转弯后直行，采用改进型单轴旋转方案的惯性导航系统位置精度明显优于采用常规两位置方案的惯性导航系统。

4 结论

本文针对单轴旋转调制式惯导系统，研究了水平方向惯性仪表常值误差旋转自补偿的机理，在此基础上针对载体转弯时存在水平方向惯性仪表误差自补偿不完全的问题，提出了一种改进型单轴旋转调制方案，理论推导表明在载体方位发生变化时，该方案可以克服常规调制方案存在的因载体航向耦合效应造成的上述误差自补偿不完全的问题，从而提高单轴旋转惯导系统在各类行驶状态下的导航精度。采用此改进方案，只需在导航过程中，对实时解算出来的载体航向角做相应的运算再确定转台合适的停止位置，实现起来比较简单。最后通过多种运动状况下的仿真计算和研究，验证了本文改进型旋转调制方案的有效性和可行性。

［1］王巍.光纤陀螺惯性系统［M］.北京:中国宇航出版社，2010. WANG Wei.Inertial navigation system with fiber optic gyro［M］.Beijing:China Aerospace Press，2010.

［2］Levinson E，Giovanni C S.Laser gyro potential for long endurance marine navigation［C］.IEEE Position Location and Navigation Symposium，Atlantic City，NJ，1980: 115-129.

［3］Levinson E，TerHorstJ，WillcocksM.Thenext generation marine inertial navigator is here now［C］.Proceedings of the IEEE Position Location and Navigation Symposium，1994:121-127.

［4］袁保伦.四频激光陀螺旋转式惯导系统研究［D］.国防科学技术大学，2007. YUAN Bao-lun.Research on rotating inertial navigation system with four frequency differential laser gyroscope［D］.National University of Defense Technology，2007.

［5］秦永元.惯性导航［M］.北京:科学出版社，2006. QIN Yong-yuan.Inertial navigation［M］.Beijing:Science Press，2006.

［6］孙伟.旋转调制型捷联惯性导航系统［M］.北京:测绘出版社，2014. SUN Wei.Rotary strapdown inertial navigation system［M］.Beijing:Surveying and Mapping Press，2014.

［7］Shang S T，Deng Z H，Fu M Y，et al.Analysis of singleaxial rotation modulation influence on FOG INS precision［C］.Proceeding of the 29thChinese Control Conference，Beijing，China，2010:5469-5472.

A Improved Single Axis Rotation Modulation Scheme of FOG Inertial Navigation System

YUE Dong-dong，CAI Chun-long
（Beijing Aerospace Times Optical-electronic Technology Co.，Ltd.，Beijing 100094）

In this paper，on the basis of traditional rotating modulation scheme，a improved fiber optic gyro inertial navigation system's single axis rotation modulation scheme is raised.The scheme studied the changes of the head angle. Through the optimization of IMU stop position，the scheme realized a better error compensation effect than the traditional modulation scheme.This paper has carried on the theoretical derivation and simulation verification to prove the validity and feasibility of this scheme.

INS；rotation modulation；FOG；single axis rotation scheme

U666.12

A

1674-5558（2016）01-01215

10.3969/j.issn.1674-5558.2016.05.007

岳栋栋，女，硕士，研究方向为光纤陀螺捷联惯性导航系统。

2015-12-15