低轨微纳卫星全磁自主导航算法研究

周琼峰，康国华，寇　鹏，范　凯，潘俊帆

（1.南京航空航天大学航天学院微小卫星研究中心，南京210016；2.西安卫星测控中心，西安710043）

低轨微纳卫星全磁自主导航算法研究

周琼峰1，康国华1，寇鹏2，范凯1，潘俊帆1

（1.南京航空航天大学航天学院微小卫星研究中心，南京210016；2.西安卫星测控中心，西安710043）

针对低轨微纳卫星体积小、功耗低的设计约束，提出了基于低轨地磁的定轨/定姿全磁自主导航算法。该算法仅利用三轴磁强计测量值和卫星动力学方程建立Kalman滤波器，实现了低轨微纳卫星的全自主轨道确定和姿态测量，理论仿真结果表明，该全磁导航算法精度能够满足低轨微纳卫星的一般要求。利用高精度地磁模拟器搭建了微纳卫星全磁自主导航地面仿真验证系统，对算法进行了全物理仿真测试和实验误差分析，进一步验证了全磁自主导航算法的可行性，为低轨微纳卫星提供了一种低成本、高自主、高可靠性的导航方法。

微纳卫星；地磁定姿；Kalman滤波；仿真验证系统

0 引言

由于体积、质量、功耗等因素的限制，传统卫星采用星敏、地平仪、GNSS等导航系统无法满足低轨微纳卫星的要求。随着地磁场模型的日趋完善，很多研究提出了利用地磁场进行自主导航的方法［2］，但往往偏重定轨或者定姿，考虑全磁导航的较少。本文仅以三轴地磁信息为测量值，构建满足低轨微纳卫星基本要求的导航系统。通过国际地磁参考场（International Geomagnetic Reference Field，IGRF）模型与三轴磁强计测量矢量作为更新信息，设计Kalman滤波器［1，3-4］，实现实时的自主定轨和无陀螺姿态确定。考虑到磁强计测量地磁场没有视场的约束，且具有成本低、质量小、可靠性高等优点，因此该方案功耗小、寿命长且可靠性高，在低轨微纳卫星非高精度自主定轨、姿态稳定任务中具有良好的应用前景。

1 数学模型与导航原理

1.1动力学模型

（1）轨道动力学模型

对于近地轨道的微纳卫星，选取地心赤道惯性坐标系，导航系统状态模型为:

式中，x、y、z、vx、vy、vz分别表示卫星在惯性坐标系下三个方向的位置和速度；μ为地球引力常数；r为卫星至地心的距离；J2为地球引力摄动系数；Re地球参考半径；Px、Py、Pz为地球非球形高阶摄动项和大气摄动加速度等。

（2）姿态动力学模型

本文全磁导航定姿算法基于卫星动力学去耦俯仰轴的二重积分模型:

式中，Ny为总的外加转矩，Iyy为卫星Y轴的转动惯量。

1.2地磁场模型

地理坐标系下，地磁场分量表示为:

1.3全磁导航原理

设轨道坐标系OXYZ是系统参考坐标系，地磁场强度记为矢量B，在轨道坐标系下的分量为Bx、By、Bz，三轴磁强计沿载体坐标系ObXbYbZb三轴方向安装，磁强计测量量记为Bb，在载体坐标系下的分量为Bbx、Bby、Bbz。

（1）定轨

三轴磁强计通过敏感地磁场可测量得到地磁参考矢量在本体坐标系下的强度和方向。地磁场矢量是位置的函数，因此通过对卫星所在位置的三轴地磁强度量测值与轨迹地磁场模型的标准值进行滤波，即可得到相对位置信息。

（2）定姿

地磁场强度在轨道坐标系和载体坐标系各轴上的投影可由两坐标系之间的转换矩阵来表示:

式中，ψ为偏航角，θ为俯仰角，γ为横滚角。

设轨道坐标系Y轴与载体坐标系Yb轴基本重合，即偏航角和滚动角都在小角度范围内，则俯仰角θ可由2个坐标系下的磁场分量计算得到:

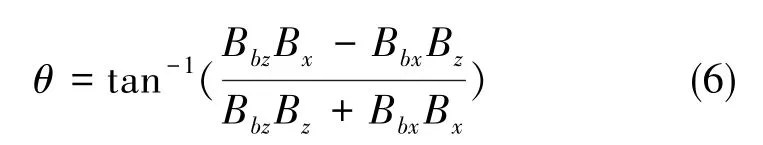
本文利用上述原理，提出了基于磁强计的卫星轨道与姿态串联确定算法。

2 滤波器设计

2.1状态方程

以轨道动力学和姿态动力学模型为基础分别建立系统状态方程。

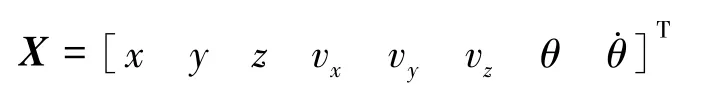
根据动力学方程，近似有:

为采样时间。

2.2观测方程

以地磁场强度矢量作为观测量时，h可表示为:

式中，Bx、By、Bz为地心固连坐标系下的分量。地固系下的量测矩阵可表示为;

根据地固系与惯性系的转换关系:

3 算法仿真

3.1仿真条件

全磁导航算法仿真流程图如图1所示。

图1　全磁导航算法仿真流程图Fig.1 Flow chart of the simulation of the magnetic navigation algorithm

根据设定的轨道参数和IGRF模型推算出地磁场矢量在轨道坐标系中随时间变化的分量，并根据卫星姿态信息仿真出相应地磁场矢量在卫星本体坐标系中的分量；然后利用姿态确定算法推导出卫星本体相对轨道系的俯仰角和角速度。

仿真初始条件:某近地点轨道半长轴6799.4km，轨道倾角65°，偏心率0.00134，升交点赤经30°，近地点角距30°，卫星惯量I=（2.224，2.326，2.316），惯量积为零。滤波器状态初始值均方误差阵P=10-6I8×8，系统噪声和测量噪声的方差矩阵分别为Q=1×10-8、R=1/3600。仿真时长4000s。

3.2仿真结果

根据轨道要素求出微纳卫星的初始位置为［4370.57 4183.41 3083.06］Tkm，初始速度为［-4.728 0.508 6.014］Tkm/s。根据卫星初始状态计算轨道磁场分量。

将上述得到的轨道磁场数据作为仿真源数据进行算法仿真，如图2～图6所示，分别为三维轨迹图（图2）、位置误差（图3）、速度误差（图4）、俯仰角真值（图5）以及俯仰角实际值（图6）。其中，俯仰角真值即为仿真初始设定的俯仰角，根据俯仰角真值仿真得到磁强计量测值。

图2　三维轨迹图Fig.2 The three-dimensional trajectory figure

图3　位置误差Fig.3 The position error

图4　速度误差Fig.4 The velocity error

图5　俯仰角真值Fig.5 The real angel of pitch

图6　俯仰角实际值Fig.6 The actual angel of pitch

利用地磁矢量进行滤波定轨时，经过对误差数据的统计得到:位置平均误差分别为5.16km、3.60km、0.69km；速度平均误差分别为3.29m/s、1.91m/s、0.38m/s；在此基础上，姿态确定俯仰角测量值平均误差为0.14°；俯仰角滤波值平均误差为0.01°。上述仿真结果可以满足微纳卫星对中等导航精度的要求。

4 系统测试

上述理论仿真验证了全磁导航算法的可行性，本文还利用地磁模拟器和自研的微纳卫星，搭建了全实物仿真环境。由于全磁导航算法实现较为复杂，定轨的误差相对较大，且实际测试环境存在不稳定的干扰磁场，为准确测试姿态确定的误差范围，本文在卫星姿态保持不变的条件下，给定轨道真值，单独对地磁定姿算法进行了测试实验，并对测试结果进行了分析，验证了基于地磁的定姿算法。

4.1测试内容

地面测试系统如图7所示，首先设定当前轨道参数，根据IGRF磁模型计算出相应的轨道磁场强度，通过控制上位机发送磁场模拟控制指令，驱动磁模拟器生成相应的磁场环境；将自研的微纳卫星置于磁模拟器产生的均匀磁环境中，使本体坐标系与轨道坐标系基本重合，即俯仰角在小角度范围内；由星上惯性测量组件ADI磁强计测量当前的环境磁场；轨道磁场强度矢量和磁强计测量矢量反馈给星上计算机，进行磁定姿算法解算；最后输出实时姿态确定信息。

图7　地面磁定姿测试系统示意图Fig.7 Schematic diagram of the ground test system

测试条件:微纳卫星的本体坐标系Yb轴与磁模拟器模拟的轨道磁场坐标系Y轴重合，微纳卫星保持姿态不变，且两坐标轴基本重合的条件下完成1h的地磁定姿测试，并记录俯仰角测量值和滤波值。

4.2测试结果与分析

地面测试系统1h姿态测量结果如图8所示，即俯仰角测量值与滤波值的变化曲线。表1为姿态测量数据分析结果。

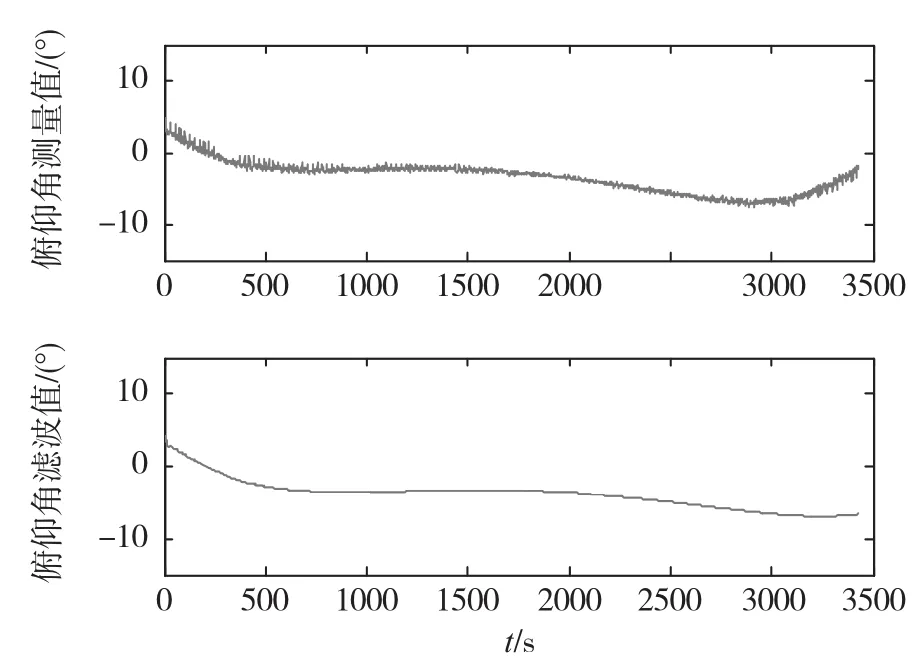
图8　俯仰角测量值和滤波值的变化曲线Fig.8 Variation curve of the real angel before and after filtering

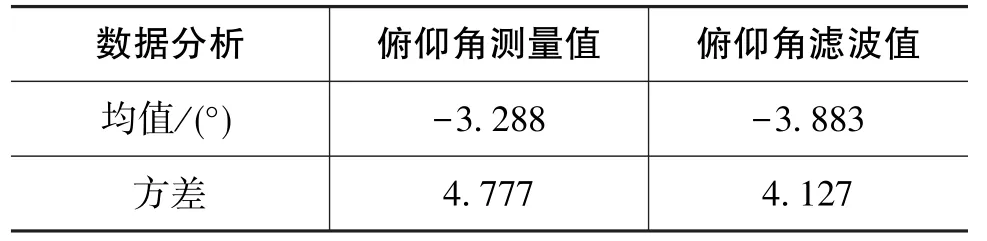
表1　姿态测量数据分析Table 1 Data analysis of attitude measurement

由图8可知，俯仰角输出平稳，表明卫星当前的姿态基本保持不变；由表1可知，当前卫星俯仰角绝对值小于5°，表明本体坐标系与轨道坐标系基本重合，符合实验条件；但由变化曲线和统计方差可知俯仰角测量值变化较明显，分析原因如下:

1）磁模拟器模拟的磁场环境与真实的轨道磁场存在实时误差；

2）星上ADI磁强计测量误差和整星剩磁；

3）周围环境磁场干扰，包括星上计算机、实验仪器以及测试人员等。

5 结论

本文提出了适用于微纳卫星的全磁导航算法，通过仿真分析以及地面测试系统的实验验证，得到以下结论:

1）通过仿真验证，该全磁导航算法精度能够满足微纳卫星对中低精度导航的要求；

2）通过搭建地面测试系统，实现了基于地磁的定姿算法，并验证了算法的可行性。

低轨全磁导航的有利条件在于:地磁强度较大，且地磁模型日益完善；磁强计属于低成本、低功耗、高可靠性器件。本文提出的全磁导航算法充分利用了上述优势，仅依赖磁强计和地磁模型完成了定轨和定姿。对导航精度要求不高的微纳卫星，该算法不仅减小了星载设备的质量，缩短了系统研制周期，降低了研制费用，而且可以减少系统对地面的依赖程度，提高导航自主性，这对推动微纳卫星技术的应用和发展具有重要意义。

［1］Söken H E，Hajiyev C.REKF and RUKF for pico satellite attitude estimation in the presence of measurement faults［J］.Journal of Systems Engineering&Electronics，2014，25（2）:288-297.

［2］刘新彦.磁技术在卫星上的应用［J］.控制工程，1998（3）:24-29. LIU Xin-yan.The application of magnetic technology in the satellite［J］.Control Engineering of China，1998（3）: 24-29.

［3］杨斌，徐广涵，靳瑾，等.磁定姿近地轨道卫星EKF与UKF算法比较［J］.中国空间科学技术，2012，32（6）:23-30+38. YANG Bin，XU Guang-han，JIN Jin，et al.Comparison between EKF and UKF algorithm of attitude determination by magnetic on low earth orbit satellites［J］.Chinese Space Science and Technology，2012，32（6）:23-30+38.

［4］朱建丰，徐世杰.基于地磁场测量估计卫星姿态的UKF算法［J］.宇航学报，2006，27（6）:1401-1405. ZHU Jian-feng，XU Shi-jie.The UKF algorithm of satellite attitude estimation based on the geomagnetic measurement［J］.Journal of Astronautics，2006，27（6）: 1401-1405.

［5］Psiaki M L，Martel F，Pal P K.Three-axis attitude determination via Kalman filtering of magnetometer data［J］. Journal of Guidance，Control，and Dynamics，1990，13（3）:506-514.

［6］Psiaki M L，OshmanY.Spacecraftattituderate estimationfromgeomagneticfieldmeasurements［J］. Journal of Guidance，Control，and Dynamics，2003，26（2）:244-252.

［7］王淑一，杨旭，杨涤，等.近地卫星磁测自主导航算法研究［J］.宇航学报，2003，24（6）:634-637. WANG Shu-yi，YANG Xu，YANG Di，et al.Algorithm for autonomous navigation of low earth orbit satellite using magnetic measurements［J］.JournalofAstronautics，2003，24（6）:634-637.

［8］王鹏，张迎春.一种小卫星高精度自主定轨/定姿一体化新方法［J］.中国惯性技术学报，2014，22（6）:741-747+754. WANG Peng，ZHANG Ying-chun.An integration methods of small satellite autonomous high precision orbit and attitude determination［J］.Journal of Chinese Inertial Technology，2014，22（6）:741-747+754.

［9］黄朝艳，田海冬，赵华.地磁滤波导航技术的研究现状［J］.科学技术与工程，2013，13（30）:8976-8982. HUANG Zhao-yan，TIAN Hai-dong，ZHAO Hua.The current research status of magnetic filter navigation technology［J］.Science Technology and Engineering，2013，13（30）:8976-8982.

［10］姜竹青.自主导航中滤波算法的研究及应用［D］.北京邮电大学，2014. JIANG Zhu-qing.The research and application of filtering algorithmin the autonomous navigation［D］.Beijing University of Posts and Telecommunications，2014.

［11］李龙鸣.地磁导航算法研究［D］.哈尔滨工业大学，2013. LI Long-ming.Research on geomagnetic navigation algorithms［D］.Harbin Institute of Technology，2013.

［12］赵钟伟.基于磁场信息的定位原理及应用［D］.浙江大学，2014. ZHAO Zhong-wei.The principle and application of position based on magnetic information［D］.Zhejiang University，2014.

［13］李会.基于地磁/低成本MEMS惯性器件复合姿态测量方法研究［D］.沈阳理工大学，2014. LI Hui.The research on composition attitude measuring method based on geomagnetic/low cost MEMS inertial components［D］.Shenyang Ligong University，2014.

［14］刘晓娜.地磁传感器及其在姿态角测试中的应用研究［D］.中北大学，2008.LIU Xiao-na.Research on magnetic sensor and its application in the attitude angle test［D］.North University of China，2008.

［15］Michalareas G，Gabriel S B，Rogers E.Spacecraftattitude estimation based on magnetometer measurements and the covariance intersection algorithm［C］.Aerospace Conference Proceedings，IEEE，2002:2205-2219.

［16］吕云霄.地磁匹配导航算法研究［D］.国防科学技术大学，2010. LV Yun-xiao.Research on geomagnetic matching navigation algorithms［D］.National University of Defense Technology，2010.

Research on Single Magnetic Autonomous Navigation Algorithm of Microsat

ZHOU Qiong-feng1，KANG Guo-hua1，KOU Peng2，FAN Kai1，PAN Jun-fan1
（1.Nanjing University of Aeronautics and Astronautics，Institute of Astronautics，Nanjing 210016；2.China Xi'an Satellite Control Center，Xi'an 710043）

An algorithm based on the low orbit geomagnetic field for satellite single magnetic autonomous navigation is proposed in this paper due to the design constraint of small volume and low power consumption of microsat.The algorithm is only based on magnetometer vector and dynamical equation，which establishes Kalman filter and then implements autonomous orbit determination and attitude measurement.The accuracy of single magnetic navigation can meet the normal requirements of microsat verified by simulation analysis.Simulation verification system on magnetic navigation is also founded.The feasibility of geomagnetic navigation algorithms is verified by test and analysis.In conclusion，a low cost navigation method with high autonomy and reliability is provided for microsat.

microsat；attitude determination based on geomagnetic field；Kalman filter；simulation verification system

TN965.7

A

1674-5558（2016）01-01218

10.3969/j.issn.1674-5558.2016.05.006

周琼峰，女，硕士，研究方向为微小卫星的总体设计和姿态控制。

2015-12-24

上海航天科技创新基金（编号:SAST2015035）；江苏省自然基金青年基金项目（编号:SBK201343261）。