发射初态误差对弹道特征参数的影响①

郑　旭，高长生，荆武兴，常晓华

(1.哈尔滨工业大学 航天工程系，哈尔滨　150001；2.北京宇航系统工程研究所，北京　100076)



发射初态误差对弹道特征参数的影响①

郑旭1，高长生1，荆武兴1，常晓华2

(1.哈尔滨工业大学 航天工程系，哈尔滨150001；2.北京宇航系统工程研究所，北京100076)

弹道导弹发射初态误差会影响动力学方程中引力加速度和视加速度项，进而影响空间弹道并带来导航误差。针对这一问题，分析了发射初态误差的传播过程和影响机理，提出了以小扰动法建立考虑视加速度耦合的导航摄动方程，推导了导航摄动方程的解析解。仿真得出了发射初态误差产生的关机点和落点的传播矩阵，计算了在不同发射方位角和不同发射点情况下产生的关机点和落点偏差，分析了其传播过程，定量地给出了影响量级。结果表明，所建立的解析解法能够很好地与数值解相吻合，其中高程偏差较小时视加速度耦合带来的关机点误差很小；初始定位误差是产生引力加速度偏差的主要影响因素，初始定向偏差是产生视加速度偏差的主要影响因素。

弹道导弹；发射初态误差；视加速度耦合；导航摄动方程

0　引言

引起弹道导弹落点偏差的因素包括制导工具误差和制导方法误差，这两种误差一直是国内外研究的对象。随着制导设备性能的不断改进，制导工具误差引起的落点偏差有所下降，而制导方法误差的影响日渐突出，而本文所研究的发射初态误差属于制导方法误差。弹道导弹发射前要进行平台的调平和对准，但由于地球是一个极其复杂不规则的椭球体，实际的平台坐标系与理论发射惯性系会产生初始定位误差和初始定向误差，导致了发射初态误差的产生。在通常的弹道计算中，都是直接将平台坐标系中输出的视加速度在发射惯性系中进行计算，这样就会造成视加速度投影偏差。另外，由于弹道导弹初始位置误差和初始速度误差的存在，实际飞行中会造成导弹空间位置的不同，进而带来空间引力加速度偏差。因此，发射初态误差通过影响引力加速度和视加速度的大小和方向，产生空间状态偏差，随之也会带来导航和制导误差，最终影响关机点状态偏差和落点偏差。资料表明，对于10 000 km射程的远程弹道导弹，机动发射时初态误差引起的落点偏差达到千米量级。因此，开展发射初态误差的研究对于分析远程弹道导弹命中精度具有十分重要的意义。

目前，国内外学者针对发射初态误差的影响机理作了较多的研究。Gore R C[1]忽略地球自转和扁率的影响，导出了初始定位误差和坐标基准偏差产生状态偏差计算方法，但由于简化太多，使得计算结果误差较大。Volgyesi L[2]、Featherstone[3]研究了发射点垂线偏差的形成规律及影响机理，并分析了垂线偏差传播规律。Wang J Q 等[4]建立了远程弹道导弹目标点位置偏差与垂线偏差的函数关系式，并分析得出垂线偏差可造成1 km量级的落点偏差，每提高1″的精度，落点偏差可减少85 m。贾沛然[5]详细分析了弹道导弹在定时关机和射程关机两种情形下垂线偏差对命中精度的影响。王明海[6]、杨辉耀[7]将发射初态误差统一为标准发射坐标系与实际发射坐标系的平移和旋转，并求出了落点偏差与各初态误差项的关系表达式。郑伟[8-9]建立了弹道导弹定位定向误差传播模型，计算了定位定向误差产生的几何项偏差、初值项偏差和受力项偏差的影响量级，并推导了高程偏差与视加速度耦合的传播方程。段晓君等[10]分析了发射点定位误差产生的发射方位角误差大小，并通过仿真得出了其对弹道特性的影响规律。

国内外学者对于研究发射初态误差的传播规律取得了一定的研究成果，但缺乏系统深入的研究。本文通过分析发射初态误差的传播规律，得出发射点大地经纬度偏差是产生关机点x和z方向位置偏差的主要因素，主要通过引力加速度项进行传播；初始定向误差是产生关机点速度偏差的主要因素，主要通过视加速度项进行传播。

1　导航摄动方程

设理论发射点和实际发射点分别为On、Op，发射惯性系On-xayaza的y轴方向指向当地重垂线的反方向，为制导计算坐标系，如图1所示。发射惯性系Op-xpypzp是利用惯性测量平台的输出进行实际定位定向，为平台坐标系。

由此看出，On-xayaza和Op-xpypzp的差别包括天文经度误差ΔλT、天文纬度偏差ΔBT、天文方位角误差ΔAT、大地经度误差Δλ0、大地纬度偏差ΔB0和高程偏差ΔH0，即发射初态误差向量ΔPa=[ΔλTΔBTΔATΔλ0ΔB0ΔH0]T。ΔPa会带来初始定位误差、初始定向误差、初始速度误差，传播过程如图2所示。

图1　发射初态误差作用下的2种发射惯性系

图2　发射初态误差的传播过程

由弹载计算机进行计算的导航方程:

(1)

制导计算坐标系中的导航方程:

(2)

(3)

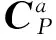
(4)

其中，初始位置误差Δra(0)=[03×3-Gr0]ΔPa，Gr0为初始定位误差传播矩阵，其表达式为[8]

(5)

式中Re为发射点地心距。

初始速度误差为Δva(0)=Gv0ΔPa，初始速度误差中的Gv0为误差传播矩阵，表达式为[9]

(6)

2　发射初态误差与视加速度耦合情况下导航摄动方程的解析解

发射初态误差产生的视加速度偏差可以表示成状态偏差的函数[8]，即

(7)

式中Mv为气动力偏差中的速度偏差产生的传播矩阵；Mr为推力和气动力偏差中的位置偏差产生的传播矩阵；Rj为指向y轴的单位向量。

传播矩阵Mv、Mr为

(8)

其中

式中Cx、Cy分别为阻力系数和升力系数；Se为发动机喷口面积；Sm为迎风面积；m为导弹当前时刻的质量；φ为俯仰角；ψ为偏航角；θ为弹道倾角；σ为弹道偏角；ρ为大气密度；β为计算大气密度和压强的常数，大小为1/7 110。

(10)

(11)

式(10)的解为

状态转移矩阵Φ(tk)的解见文献[11]，令

(13)

(14)

由此看出，发射初态误差会产生引力加速度偏差和视加速度偏差，相应的传播矩阵为引力偏差传播矩阵Cg、视加速度偏差传播矩阵CW。Cg包括两部分：一是空间位置偏差而产生的引力加速度偏差传播矩阵Cra；二是由发射初态误差产生的引力加速度偏差传播矩阵CPa。CW包括视加速度投影偏差传播矩阵CWP和高程偏差引起的视加速度耦合传播矩阵CWR。式(12)可改写为

(15)

假设导弹耗尽关机，主动段关机点为K，关机点在发射惯性系的状态量为Xk，则状态偏差量为ΔXk=[ΔvkΔrk]T。落点纵向和横向偏差为ΔL、ΔZ，与ΔXk的关系为

(16)

因此，导弹落点偏差与发射初态误差参数的关系为

(17)

式(17)就建立了发射初态误差参数到导弹落点偏差的传播关系，CP矩阵即为传播矩阵，反映了发射初态误差影响落点偏差的程度。

3　仿真校验

3.1算例1

仿真采用三级固体弹道导弹，射程为10 000 km左右，发射点大地经度为117.3°，大地纬度为39.9°，高程为10 m，发射方位角为30°。选择大地经度偏差Δλ0、纬度偏差ΔB0=10″，高程偏差ΔH0=5 m，天文经度偏差ΔλT、天文纬度偏差ΔBT、天文方位角偏差ΔAT均为10″。

3.1.1对关机点状态的影响

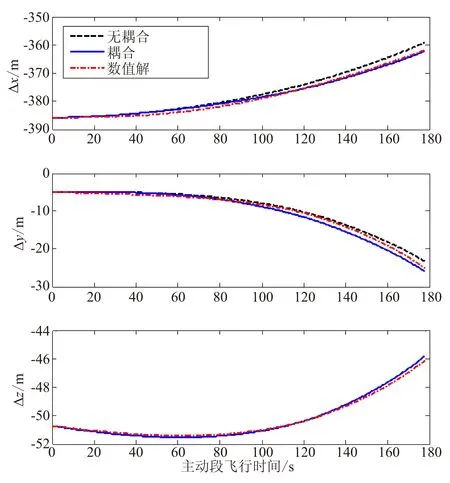
在主动段飞行过程中，发射初态误差产生的位置和速度偏差如图3所示，红色点划线是采用数值解得出的主动段状态偏差，黑色虚线是不考虑视加速度耦合情况下利用传播矩阵计算出的主动段状态偏差，蓝色实线是考虑视加速度耦合情况下计算出的主动段状态偏差。

(a) 位置偏差

(b) 速度偏差

从图3可看出，当高程偏差较小时，考虑视加速度耦合和不考虑视加速度耦合所得到的主动段状态偏差均能够与数值解吻合得很好，这表明通常情况下忽略视加速度耦合的影响是合理的。在不考虑视加速度耦合情况下，利用导航摄动方程计算得到的关机点速度偏差与数值解相差为0.03 m/s，位置相差为2.8 m，说明采用解析解的估计方法不仅能够分析出发射初态误差的传播规律，而且精度高、计算时间少。

在所给定的发射初态误差参数中，仿真计算得到了式(15)中传播矩阵Cg、Cra和CPa，如表1所示。从Cg各列中看出，ΔλT主要影响关机点z方向的速度和位置；ΔBT主要影响y和z方向的速度和位置；ΔAT、Δλ0和ΔB0主要影响x和z方向的速度和位置；ΔH0对各方向的速度和位置的传播虽然很小，但ΔH0数值较大，若忽略则可能导致较大的关机点偏差。Cra中存在较大的数值，为Cg的主要部分，如Cra和Cg第4、6行中大地经纬度偏差Δλ0、ΔB0产生的传播系数，这反映了关机点x和z方向位置偏差主要是由于发射点Δλ0和ΔB0偏差产生的。传播矩阵Cg产生的关机点速度偏差为Δvga=[0.040 0.013 -0.021]Tm/s，位置偏差为Δrga=[-381.8 -3.8 -54.8]Tm；Cra产生的速度偏差为Δvra=[0.032 -0.063 -0.020]Tm/s，位置偏差为Δrra=[-380.0 -10.7 -54.4]Tm；而由CPa产生的主动段关机点速度偏差为ΔvPa=[0.008 0.076 -0.002]Tm/s，位置偏差为ΔrPa=[-0.3 6.9 -0.2]Tm。从关机点偏差结果看，CPa所产生的关机点状态偏差量相对Cra较小，因此在初步的关机点状态估算中可忽略CPa的影响，用Cra来代替Cg。

表1　传播矩阵Cg、Cra、CPa大小

传播矩阵CW为CWP、CWR之和，WWR很小，这里给出CWP、CWR，如表2所示。

表2　传播矩阵CWP、CWR大小

从传播矩阵CWP各列中看出，ΔλT主要影响关机点x和y方向的速度和位置，比Cg中产生的传播要大；ΔBT产生的CW中传播均比Cg中的传播大，因而对关机点3个方向速度和位置影响较大；ΔAT产生关机点z方向的位置偏差的传播最大，为3.636 2×105；初始定位误差Δλ0、ΔB0和ΔH0产生的CWP矩阵中的传播为零。另外，ΔPa通过CWP产生的关机点速度偏差为ΔvWP=[0.237-0.3890.148]Tm/s，位置偏差为ΔrWP=[19.6-21.89.0]Tm。

从CWR中可看出，发射初态误差项中只有ΔH0通过CWR进行传播；传播矩阵CWR中的数值与CWP相比相差甚小；通过CWR产生的关机点速度偏差为ΔvWR=[0.0260.0130.000]Tm/s，位置偏差为ΔrWR=[2.21.10.0]Tm。因此，CWP产生的关机点状态偏差是CW产生的状态偏差的主要部分，CWR对关机点的影响可忽略不计。

基于以上分析，将Cg和CW产生的关机点状态偏差量列于表3中，将不考虑视加速度耦合和考虑视加速度耦合产生的关机点状态偏差与数值解进行对比。从中可看出，发射初态误差ΔPa通过Cg产生的关机点速度偏差相对CW较小，但是Cg产生的关机点x和z方向的位置偏差却较大，这表明ΔPa产生的关机点状态偏差包括两部分：一是发射点大地经纬度偏差Δλ0、ΔB0产生关机点x和z方向的位置偏差，主要通过Cg矩阵进行传播；二是初始定向误差ΔλT、ΔBT和ΔAT主要通过影响视加速度项偏差产生关机点速度偏差，由CW矩阵进行传播，这部分速度偏差是造成关机点总速度偏差的主要部分，通过CW矩阵进行传播所产生关机点位置偏差是主动段飞行过程中新产生的。

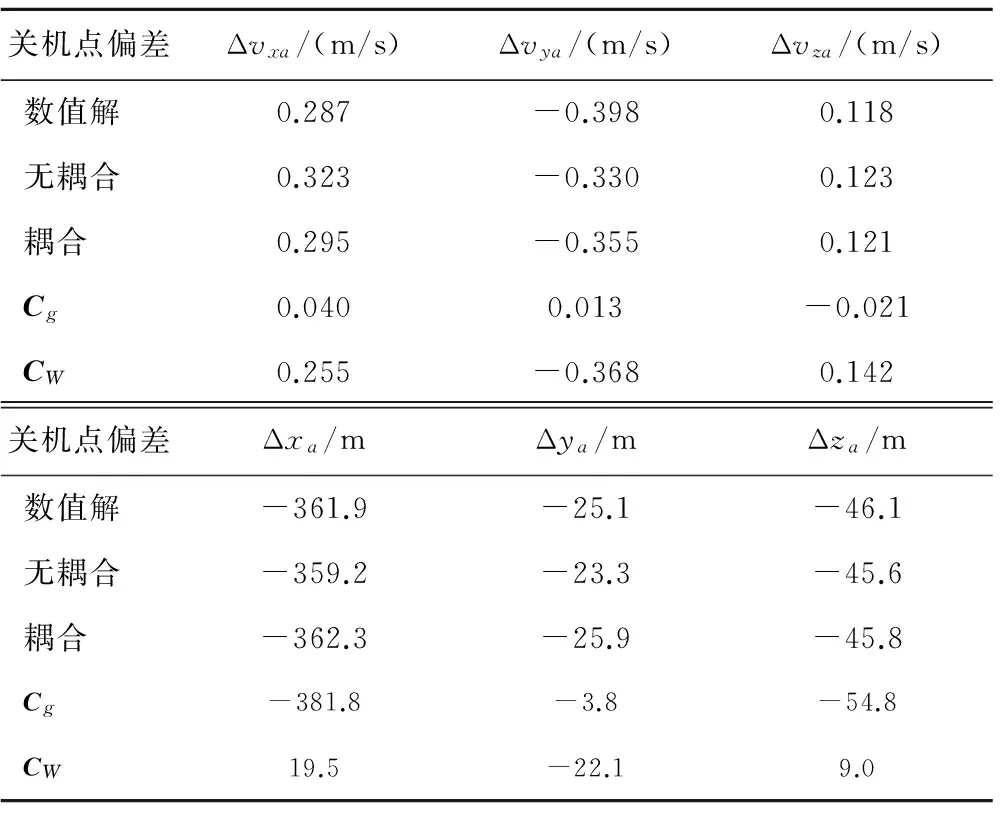
表3　关机点状态偏差量

3.1.2对落点偏差的影响

利用传播矩阵Cg和CW以及落点偏差对关机点状态的偏导数CX即可得出由发射初态误差参数引起落点误差的传播矩阵CP，通过式(16)或式(17)便可求出落点的纵向和横向偏差。表4为算例1中给定的发射初态误差下得出的传播矩阵CX和CP大小。表5为得出的导弹落点相关参数。

从CX中可看出，关机点速度偏差引起落点偏差的传播因子较大，如x方向速度偏差引起的纵向和横向偏差传播因子分别为5.574 5×103、1.066 2×103，而关机点位置偏差传播因子较小，但是关机点位置偏差比速度偏差大，因此均会产生较大偏差。另外，纵向误差传播矩阵∂L/∂Xk中的值明显大于横向误差传播矩阵∂L/∂Xk。

表4　传播矩阵CX和CP大小

表5　导弹落点相关参数

从CP矩阵中可看出，高程偏差ΔH0对落点偏差影响因子最小，对应的纵向和横向传播因子分别为-4和-1，因此高程偏差产生的落点纵向和横向偏差分别为-20 m和-5 m。在发射初态误差产生的纵向误差传播因子中，ΔBT对纵向偏差影响最大，传播因子为1.754 8×107，造成的纵向偏差为850.8 m，在纵向偏差中占有大部分的比重；其次ΔλT产生的传播因子也较大，为0.3761×107；然后依次是ΔAT、ΔB0和Δλ0。在横向偏差传播因子中，ΔAT对横向偏差的影响最大，大小为0.647 5×107，造成的横向偏差为313.9 m，为横向偏差中的主要部分；其次Δλ0和ΔB0对横向偏差的传播因子也较大，分别为0.187 8×107和-0.353 1×107，也是对横向偏差影响的主要部分；最后ΔλT和ΔBT产生的传播因子相对较小，分别为0.016 3×107和-0.056 4×107。

表5得出了弹道导弹落点偏差、射程、射程角以及球面方位角。表5中给出了通过传播CP求解和数值解得出的射程偏差和横向偏差，利用CP得出的落点偏差为780.4 m，数值解为804.8 m，相差24.4 m，误差3%，由此看出，利用传播CP求解与数值解计算的落点偏差相符的很好。

3.2算例2

算例1分析了在固定发射地点、固定发射方位角情况下发射初态误差ΔPa的传播规律，下面将分别分析在固定发射地点、不同发射方位角以及固定发射方位角、不同发射地点两种情况下ΔPa产生的关机点状态偏差和落点偏差，并给出估计精度。

这里发射初态误差参数仍采用算例1中的偏差项ΔPa，表6为在不同发射方位角情况下关机点状态偏差和落点偏差。为叙述方便，这里以A0=0°为例，第1行为导弹在ΔPa条件下通过数值计算得到的关机点状态偏差和落点偏差，第2行为通过导航摄动方程解析解方法得出的关机点状态偏差和落点偏差。

从表6可看出，通过解析解法得出的关机点速度大小偏差为0.493 m/s，数值解为0.461 m/s，相差0.032 m/s；解析解法得出的关机点位置大小偏差为359.5 m，数值解为364.7 m，相差为5.2 m；解析解法产生的落点偏差为751.4 m，数值解为695.9 m，相差为55.5 m，圆概率偏差(CEP)误差百分比为7.97%。从不同发射方位角产生的落点偏差看出，通过解析解法得出的偏差数据精度较高，与实际吻合得很好，落点偏差的误差均在10%左右，具有较好的适用性。

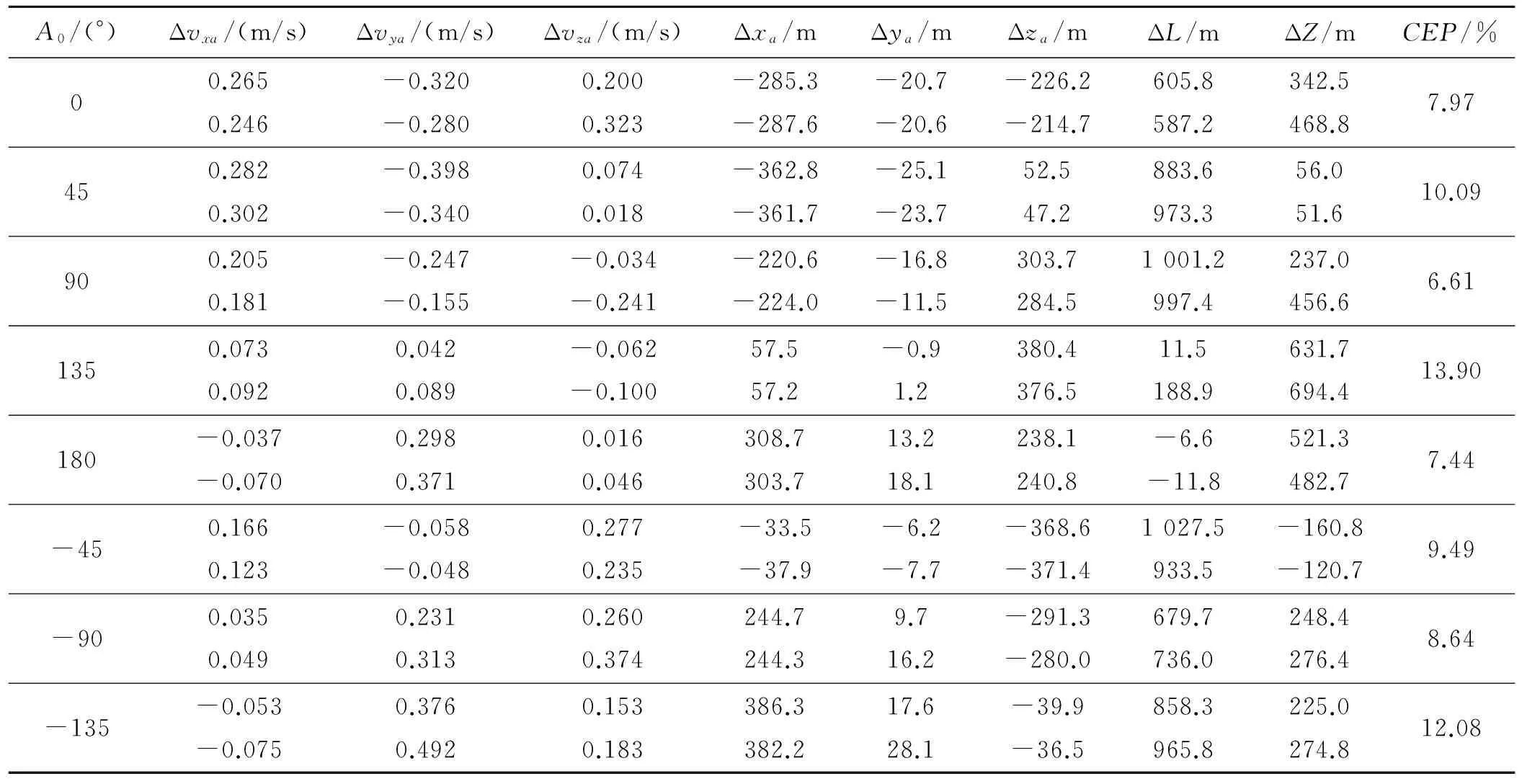
表6　不同发射方位角产生的解析解与数值解关机点状态偏差和落点偏差

由表7可看出，在发射初态误差ΔPa和发射方位角A0一定的情况下，不同发射点产生的关机点状态偏差和落点偏差。这里发射点以兰州为例，解析解法得出的关机点速度偏差大小与数值解相差为0.065 m/s，位置偏差相差为8.5 m；解析解法产生的落点偏差为775.2 m，数值解为836.5 m，相差61.3 m，CEP误差百分比为7.32%。从7表中数据看出，解析解法计算出的关机点状态偏差和落点偏差与数值解相差较小，落点偏差的误差均在10%以内，说明了该解析解法具有较高的估计精度。

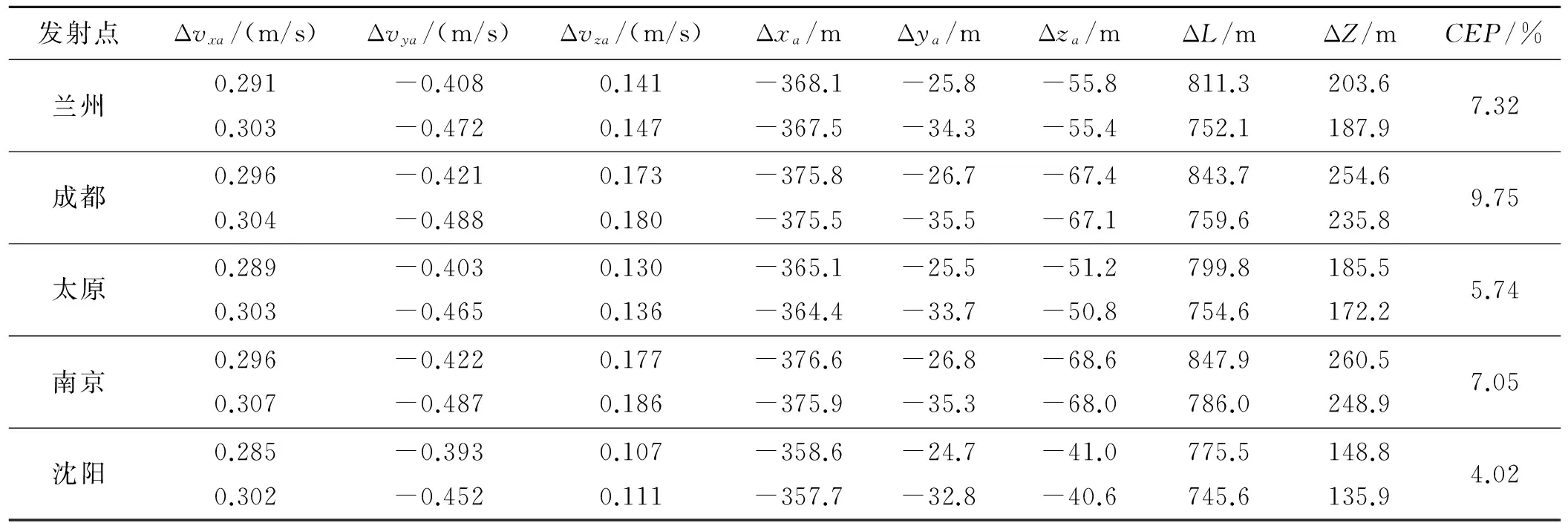
表7　不同发射点产生的解析解与数值解关机点状态偏差和落点偏差

4　结论

(1) 分析了发射初态误差的传播过程及影响机理，提出了以小扰动假设建立考虑视加速度耦合的导航摄动方程，根据微分方程理论导出了导航摄动方程的解析解。

(2) 在算例1中计算出了Cg、CW和CP传播矩阵，并验证了解析解与数值解的一致性；在算例2中列出了不同发射方位角和不同发射点产生的关机点、落点偏差的解析解和数值解，进一步验证了该解析解法具有较好的适用性。

(3) 初始定位误差主要通过Cg矩阵进行传播，其中大地经纬度偏差是影响关机点x和z方向位置偏差的主要因素。Cg包括Cra和CPa两项，在初步的误差估计中CPa影响较小，可忽略不计。

(4) 初始定向误差主要通过CW矩阵进行传播，是产生关机点速度偏差的主要因素。CW包括CWP和CWR两项，其中CWR造成的影响很小，可忽略不计。

[1]Gore R C. The effect of geophysical and geodetic uncertainties at launch area on ballistic missile impact accuracy[R].AD602214, 1964.

[2]Volgyesi L. Interpolation of deflection of the vertical based on gravity gradients[J]. Periodica Polytechnica. Civ. Eng., 1993, 37(2): 137-166.

[3]Featherstone W E, Rueger J M. The importance of using deviations of the vertical for the reduction of survey data to a geocentric datum[J]. Aust. Surv., 2000, 45(2): 46-61.

[4]Wang Jian-Qiang, Wu Hua-Ling. The impact of vertical deflection on the ballistic missiles for direction and positioning[J]. Applied Mechanics and Materials, 2014, 568-570:938-943.

[5]贾沛然. 垂线偏差对弹道导弹命中精度的影响[J]. 国防科技大学学报, 1983, 5(1): 39-53.

[6]王明海, 杨辉耀, 何浩东. 垂线偏差对导弹命中精度影响研究[J]. 飞行力学, 1995, 13(2): 90-95.

[7]杨辉耀. 大地测量误差对导弹精度的影响与修正[J].飞行力学, 1998, 16(1): 43-49.

[8]郑伟. 地球物理摄动因素对远程弹道导弹命中精度的影响分析及补偿方法研究[D].长沙: 航天与材料工程学院, 2006.

[9]郑伟, 杨华波, 汤国建. 定位定向误差对弹道导弹主动段运动的影响分析[J]. 弹道学报, 2008, 20(4): 5-7.

[10]段晓君, 姚静, 周海银. 发射点定位误差对发射方位角的影响[J]. 中国空间科学技术, 2003, 10(4): 52-56.

[11]陈国强. 远程弹道导弹误差传播特性[J]. 宇航学报, 1984, 12(3): 50-65.

(编辑：吕耀辉)

Effect of launch initial state errors on ballistic characteristic parameters

ZHENG Xu1, GAO Chang-sheng1, JING Wu-xing1, CHANG Xiao-hua2

(1.Department of Astronautics Engineering, Harbin Institute of Technology, Harbin150001, China;2.Beijing Institute of Astronautical System Engineering, Beijing100076, China)

This paper is concerned with propagation law of launch initial state errors by affecting the gravitational and apparent acceleration of the dynamics equation, which leads to state deviation of three-dimensional trajectory and navigation errors for ballistic missile. The propagation process and influence mechanism of the initial state errors were analyzed. On this basis, the navigation perturbation equation with visual acceleration coupling was established by small disturbance method. Finally, the analytical solution of navigation perturbation equation was derived. The propagation matrices and deviations of the shutdown point and the placement at different launch azimuths and different launch points were obtained, and the propagation process from launch to shutdown point and placement was analyzed, and then the quantitative magnitude from the derived propagation matrices was obtained. The results show that the analytical solution can well match the numerical solution, and the influence of apparent acceleration coupling at shutdown point is negligible. Moreover, the initial positioning errors are the main factors to produce gravitational acceleration deviation, and the initial orientation errors are the main factors to produce visual acceleration deviation.

ballistic missile；launch initial state error；visual acceleration coupling；navigation perturbation equation

2015-03-25；

2015-04-20。

国防973项目(613222)。

郑旭(1988—)，男，博士生，研究方向为飞行器动力学、制导与控制。E-mail:zhengxu_hit@hotmail.com

高长生(1978—)，男，副教授。E-mail:gaocs@hit.edu.cn

V412.1

A

1006-2793(2016)03-0436-08

10.7673/j.issn.1006-2793.2016.03.027