基于分数阶微积分理论的新型三维末制导律①
2016-11-03叶继坤韦道知雷虎民
叶继坤,韦道知,李 炯,邵 雷,雷虎民
(空军工程大学 防空反导学院,西安 710051)
基于分数阶微积分理论的新型三维末制导律①
叶继坤,韦道知,李炯,邵雷,雷虎民
(空军工程大学 防空反导学院,西安710051)
针对机动目标拦截问题,设计了一种基于分数阶微积分理论的新型三维末制导律。首先,介绍了分数阶微积分理论的定义及其相关性质,通过分析弹目拦截的空间几何关系,基于传统比例导引律(Proportional Navigation简称PN),设计了分数阶微积分比例制导律(Fractional order calculus proportional navigation简称FOCPN);其次,对设计FOCPN制导律的过载特性及其能量控制特点进行研究,通过分析前置角的变化,研究了FOCPN制导律的弹道平稳度;同时,运用小偏量运动学模型,分析了FOCPN对自动驾驶仪参数变化的鲁棒特性。最后,通过仿真表明,新设计的FOCPN制导律制导精度高,拦截时间短,过载变化较为平稳,解决了传统PN末端视线角速率发散导致的过载激增问题,可有效拦截机动目标。
分数阶微积分;制导;比例导引;过载;弹道
0 引言
比例导引因其使用简单,而被广泛应用[1-3]。然而,传统的比例导引在拦截机动目标时,由于末端视线角速率快速旋转,容易导致过载饱和[4-6],许多学者对其进行了改进,设计了多种改进型比例导引律。文献[7]利用李亚普诺夫方法,设计了针对机动目标和非机动目标改进型比例导引律,并对制导参数进行了优化,解决了视线角速率延迟导致的制导精度低的问题。文献[8]针对高速非机动目标,设计了一种可控制末端攻击角的改进型比例导引律,并对制导律的捕获区域进行了研究。文献[9]通过最小化控制能量,设计了一种最优化比例导引律,并研究了比例导引系数对最优化的影响。以上制导律的设计主要是通过增加PN对目标机动加速度、视线角速率延迟误差等控制项来改善传统PN的制导性能,主要利用视线角速率的整数阶微分项对视线角速度的非整数阶微分,一直没有深入研究和应用。
近年来,随着分数阶微积分理论的发展,分数阶微积分理论在工程中得到越来越广泛的应用。分数阶系统特有的记忆功能、线性系统稳定等特点,使其在制导控制领域也得到越来越多的应用。文献[12]将分数阶微积分理论在高超声速飞行器控制中的应用进行总结,与传统PID相比,分数阶微积分控制具有更好的鲁棒性和控制精度。文献[13]将分数阶理论用于扩散系统,解决输入磁滞问题,通过最小化积分误差思想,设计了比例型分数阶微积分控制器,相对于整数型微积分控制器,分数阶微积分控制器表现出更好的控制特性。文献[14]基于Lyapunov稳定性理论设计了分数阶混沌控制器,该控制器具有较好的响应速度和控制精度,并通过仿真,对控制算法的有效性进行验证。针对制导炮弹控制系统中系统参数出现较大的非线性和时变性等问题,文献[15]将分数阶控制器用于其飞行控制系统的设计中,提出了制导炮弹分数阶控制器参数整定的一种方法,该方法整定出的控制器参数,使系统具有较强的鲁棒性和抗干扰能力,为分数阶控制器在制导炮弹控制系统中的应用提供了参考。文献[16]提出了一种基于分数阶傅里叶变换的弹载SAR成像算法,通过最优化分数阶微积分的阶次,能对目标区域精确成像,为末制导提供更加准确的目标信息,提高了制导精度。文献[17]将分数阶微积分理论引入制导领域,设计了基于分数阶微积分PDλ比例导引规律。研究表明,设计的PDλ制导律可有效提高导弹的拦截性能。文献[18]通过对传统比例导引进行改进,针对机动目标设计了分数阶修正比例导引,并通过Lyapunov函数,证明了设计的制导律能在有效时间内收敛。由于文献[17-18]制导律研究主要是在二维平面且限制条件较多,在实际工程应用中,缺乏使用价值。
为克服上述制导律设计的缺点,本文针对三维空间中机动目标,研究分数阶微积分理论在制导律设计中的应用。首先,介绍了分数阶微积分的基础知识和性质;其次,将分数阶微积分理论应用到飞行器制导律研究中,在三维空间设计新型FOCPN;最后,从过载特性、弹道平稳度及制导系统鲁棒性等方面,分析FOCPN的制导特性,并进行仿真验证。
1 预备知识
定义:对于分数阶微积分算子,通常有如下定义[10-11]:
(1)
式中α为上限;t为下限;p为分数阶微积分算子的阶数。
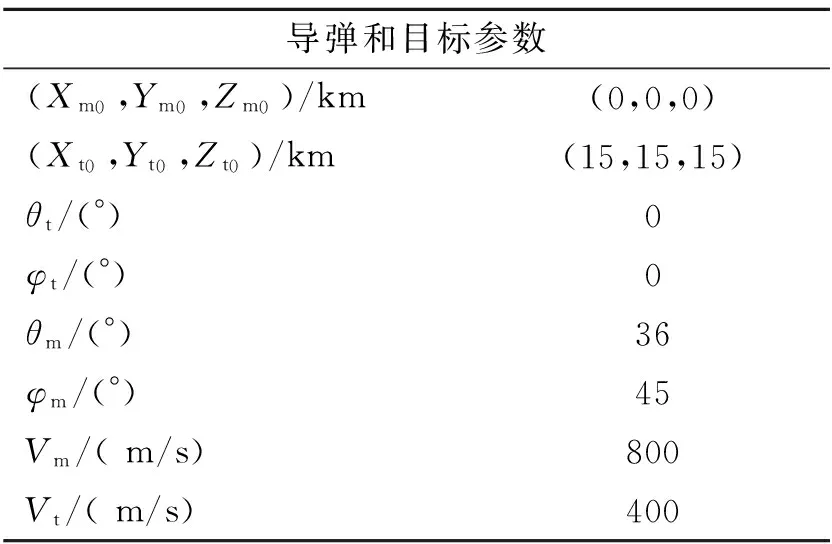
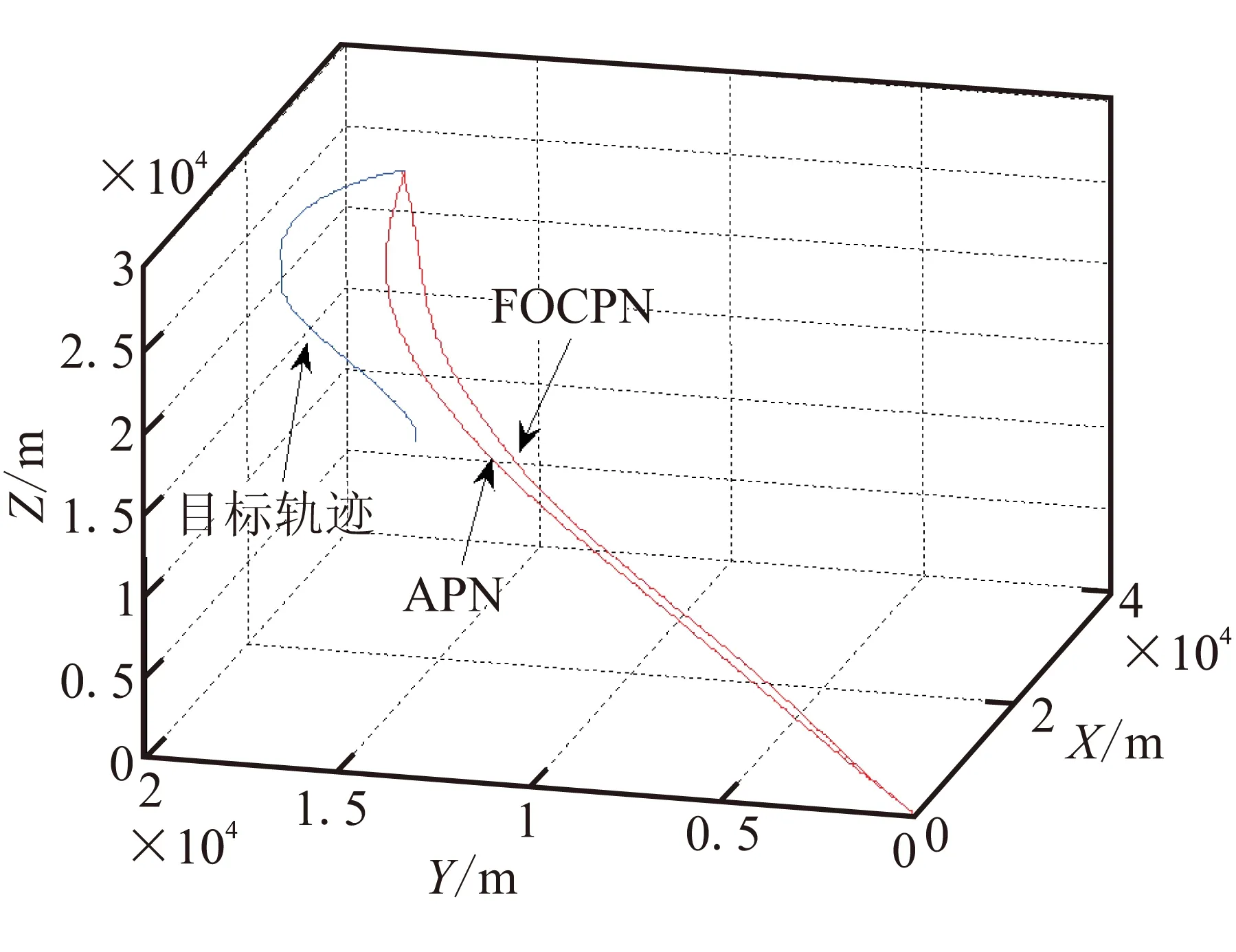
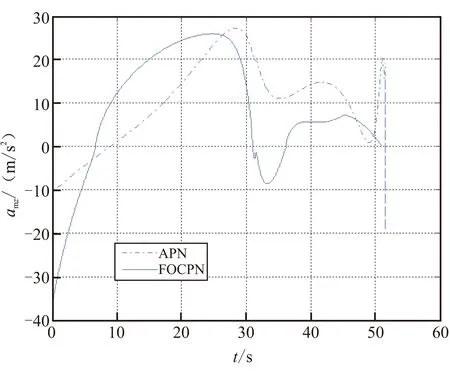
函数f(t)在定义域上n阶可导,m-1 Caputo微分定义: (2) Caputo积分定义: (3) 其中,Γ(x)表示伽马函数,它是阶乘函数n!的进一步推广,即它允许n取非整数或者复数,伽马函数的定义如下: (4) Caputo分数阶导数的Laplace变换可表示为 (5) 设函数f(t)在区间[a,t]内连续,且n阶连续可导,其n阶导数可表示为 (6) 当用非整数p代替整数n,并由Γ函数取代二项式系数,就可得Grunwald-Letnikov导数定义: (7) 从上面推导可看出,整数阶微积分是分数阶微积分的特殊形式。可以说,分数阶导数与过去所有点的信息有关,包含着完整的历史信息,而整数阶导数与最近的几个点的信息有关,只包含局部信息。从式(7)可看出,分数阶导数不仅具有记忆功能,而且越近的点影响越大,越远的点影响越小[10,19]。 因此,本文利用分数阶线性系统的良好记忆功能及其稳定性,将分数阶微积分相关理论用于制导律设计中。 导弹和目标交战时相对关系如图1所示。 图1中,M导弹,T为目标,OXMYMZM表示惯性坐标系,OXLYLZL表示视线坐标系,r为弹目相对距离,θL和φL表示视线倾角和视线偏角,θm和φm表示导弹的弹道倾角和弹道偏角,θt和φt表示目标航迹倾角和航迹偏角。 图1 弹目相对运动关系 传统TPN可表示为 (8) (9) (10) (11) 由式(10)和式(11)可知,分数阶比例型制导律主要由两项组成:一项是与视线角速率整数阶成正比的比例项;第二项是视线角速率分数阶微分的修正项,P为分数阶微分项,作为比例导引的修正补偿系数。这样设计的制导律克服了传统PN制导时只含有整数阶视线角速率值的情形,包含有视线角速率的历史信息,能更加全面地描述弹道特性,同时也更有利于对导弹的控制。下面将对设计制导律的弹道特性、过载特性以及鲁棒特性进行分析讨论。 3.1FOCPN平均过载分析 在式(10)和式(11)中,令 此时,FOCPN可表示为 (12) (13) 根据FOCPN表达式可知,制导律的平均过载可表示为 (14) 在式(14)中,令 其中 同理可得 因此,垂直平面内平均过载可表示为 (15) 同理,可得 (16) 因此,FOCPN的平均过载可以表示为 (17) 传统的TPN过载可表示为 (18) 其中,KTPN1和KTPN2为TPN平均过载的系数。 根据式(17)和式(18)可知,平均过载的大小与弹目视线角变化密切相关,当弹目视线角变化较大时,平均过载变化较大。数值仿真运算表明,当FOCPN与PN比例系数大小接近时,分数阶TPN与传统TPN平均过载大小接近。 3.2FOCPN弹道平直性分析 弹道的起伏大小与视线角增量密切相关,如果弹目视线角在一个较小区域变化,那么导弹的弹道较为平直,这对导弹执行机构要求降低,有利于导弹的设计。 导弹和目标构成的弹道前置角可分别表示为 (19) (20) 由于垂直平面和水平面内弹道特性分析相似,在此只对垂直平面内的弹道特性进行理论分析,利用同样方法,可求取水平面内的前置角变化,分析弹道平直性,将式(19)两边微分,可得 (21) 导弹的弹道倾角变化率可表示为 对式(21)两边积分,可得 (22) (23) 如果初始ηm0=0,则式(23)变形后,可得 (24) 对于传统的TPN制导,在垂直平面内,其前置角变化可表示为 (25) 根据式(24)和式(25)可知,在拦截的过程中,分数阶项的引入,使得FOCPN前置角变化较小,即在整个拦截过程中,弹道变化幅度较小,这也进一步加大了弹道的平稳度,降低了对于执行机构的过载要求。如果使设计的制导律保持弹道平直,同时降低导弹的过载要求,则必须满足下列条件: (26a) (26b) 根据式(26a)、式(26b)可知,FOCPN过载满足下列关系式: (27) (28) 由于渐近满足式(26a)、式(26b),可得 (29) (30) 导弹垂直方向和水平方向的需用过载极值,可分别表示为Nmy=max{|Ua|}/g和Nmz=max{|Ub|}/g。根据式(24)和式(26)可知,导弹的弹道较为平直时,视线倾角和偏角都变化较小,满足Nmy→0,Nmz→0。这说明设计的分数阶比例导引律可保持导弹的指令及过载渐近趋于极小。因此,采用FOCPN制导具有最小能量控制的特点,并可使弹道变化更平稳。 为简化分析过程,将三维制导律分解到垂直和水平平面分别研究。下面在垂直二维平面内,对FOCPN的鲁棒特性进行研究,水平面内分析方法类似。 垂直平面内小偏量运动学模型如图2所示。 相关运动学方程为 (31) (32) 导弹自动驾驶仪/弹体的传递函数G(s)表示如式(33)所示: (33) 以末制导采用寻的制导为例,小偏量运动学模型下制导回路如图3所示。 图2 小偏量运动学关系 图3 FOCPN寻的制导回路 令Uy(s)/Y(s)=Gy(s),根据第2节中分数阶微积分性质可知: (34) 因此,图3中函数Gy(s)可表示为 (35) (36) 在传统的PN制导和比例微分(proportional differential简称PD)制导中,制导回路传递系数分别为 对比式(36),可知: (37) 水平面和垂直面分析类似,同样可得: (38) 根据式(37)和式(38)可知,FOCPN制导通过分数阶项的引入,增大了传递函数的增益系数,相对于传统的PN制导,这将加强对机动目标的导引能力,同时能减小对机动目标的系统误差,进一步提高制导精度。 定义:系统T对参数K的灵敏度表示为 (39) 为分析方便,推导垂直平面内的稳态系统灵敏度,计算可得 (40) 根据寻的制导系统回路图3可知,系统传递函数的误差微分可表示为 (41) (42) (43) 其中,p(s)为中间计算项。因此,根据式(41)~式(43),可知: (44) (45) (46) (47) (48) (49) 通过式(46)~式(49)可知,FOCPN对自动驾驶仪参数灵敏度由于分母项变大而导致绝对值变小。因此,相对于传统PN制导,FOCPN对自动驾驶仪参数变化具有更强的鲁棒性。 为检验设计FOCPN制导律的制导性能,在此选用比扩展比例导引(Appended Proportional Navigation简称APN)作为对比[20],仿真中步长取为0.01 s,导弹和目标的初始仿真参数设置如表1所示,APN制导的制导系数取为3.5,分数阶微积分的阶次在[0,1]范围内取值,参考文献[18],按照遍历寻优的方法,微分阶次p最优值取为0.6。在仿真过程中,选取视线转率作为基准3σ的不确定性,同时选取到导引头的测量误差为0.01 (°)/s。参考文献[21],导弹的自动驾驶仪模型表示如下: (50) 式中τ为时间常数,τ=0.5 s;ζ为阻尼常数,ζ=0.6;ωn为频率,ωn=18 rad/s。 为有效验证FOCPN制导性能,设置3种仿真情形,仿真1中目标不机动,直线飞行;仿真2中目标在倾斜平面做圆弧形机动,机动加速度设为40 m/s2;仿真3中目标机动加速度在水平和垂直方向机动加速度分别为atz=20 m/s2和aty=20 m/s2。拦截性能比较表如表2所示,其中脱靶量和拦截时间来自200次蒙特卡洛仿真。 根据仿真结果表2可知,APN和本文设计的FOCPN两种制导律都能对机动目标实施有效拦截,保证击落目标,在制导精度方面,当目标不机动时,两者制导精度相差不大。然而,目标机动飞行时,FOCPN的制导精度优于APN制导。根据2种制导律的仿真时间可知,新设计的FOCPN制导律拦截时间较短,这将使得导弹更早的将目标击落。为方便分析弹道和导弹加速度变化,下面给出仿真条件3时仿真图4~图8,以描述FOCPN弹道特性和过载变化特点。 表1 仿真初始数据 表2 APN和FOCPN性能比较 图4 弹目相对运动轨迹 由仿真图4可看出,相对于APN制导,FOCPN的弹道曲率变化较小,拦截弹飞行轨迹相对也较小,弹道的平直有利于导弹在飞行中的弹道控制。根据图5和图6可知,在拦截的初始阶段,采用FOCPN时,导弹的弹道倾角和弹道偏角快速变化,保证了导弹姿态的调整,这也使得后续末端拦截时,弹道倾角和偏角变化幅度较小。因此,能保证弹道在作战后期保持较为平稳,而APN在拦截的后期,弹道倾角和偏角变化相对较大。 图5 导弹弹道倾角变化曲线 图6 导弹弹道偏角变化曲线 图7 导弹法向加速度曲线 由图7和图8可知,采用APN制导时,在拦截的开始阶段,导弹对目标机动没有进行及时补偿,这样造成了制导后期的强制补偿。因此,弹道较为弯曲,尤其在拦截的末端,随着弹目距离的接近,横向加速度的末端出现激增现象(图8),这也是导致脱靶量较大的重要原因。而FOCPN制导时,导弹加速度变化没有出现过激现象,整体变化相对较小,在末制导的初始阶段,导弹能利用增大自身加速度调整自身的飞行姿态,补偿由目标机动引起的视线角速率变化,在拦截的末端,采用FOCPN制导能有效抑制视线的旋转,解决了传统比例导引末端视线角速率发散,导致加速度激增问题,这也降低了对导弹执行机构的设计要求。在图7和图8的33 s左右出现曲线变化,主要是因为目标机动的方向变化引起导弹过载出现变化。 图8 导弹横向加速度变化曲线 综上可知,针对非机动目标,APN和FOCPN制导性能相当。然而,对于机动类目标, FOCPN能更好地控制飞行弹道,导弹加速度变化也较平稳,表现出更加良好的制导性能。 (1)文中以传统PN制导为基础,利用分数阶微积分理论改进传统PN,设计了FOCPN制导律。通过理论分析了FOCPN制导律的过载特性、弹道特性,以及对自动驾驶仪参数的鲁棒性。 (2)针对机动目标,相对于APN制导,新设计FOCPN能够针对机动目标进行有效拦截,且制导精度髙,拦截时间短,弹道变化较平稳,能克服传统比例导引因视线角速率发散导致的过载饱和问题。 (3)所设计的制导律主要针对大气层内机动目标,如何将分数阶微积分理论引入到对临近空间高超声速目标或者导弹类目标实现直接碰撞拦截,是下一步研究的重点。 [1]Ghose D.True proportional navigation with maneuvering target[J].IEEE Transaction on aerospace and electronic systems,1994,30(1):229-237. [2]Guelman M.A qualitative study of proportional navigation[J].IEEE Transaction on aerospace and electronic systems,1971,7(4):637-643. [3]Guelman M,Shinr J.Optimal guidance law in the plane[J].IEEE Journal Guidance and Control Dynamic,1996,7(4):471-476. [4]张旭,雷虎民,曾华,等.带落角约束的自适应比例制导律[J].固体火箭技术,2011,34(6):687-692. [6]Talole S E,Banavar R N.Proportional navigation through predictive control[J].IEEE Journal Guidance and Control Dynamic,1998,21(6):1004-1006. [7]Li C Y,Jing W X.Geometric approach to capture analysis of PN guidance law[J].Aerospace Science and Technology,2008,12:177-183. [8]Dhananjay N,Lum Kai-yew,Xu Jian-xin.Proportional navigation with delayed line-of-sight rate[J].IEEE Trans.on control system technology,2013,21(1):247-253. [9]Satadal Ghosh,Debasish Ghose and Soumyendu Raha.Three dimensional PN based impact angle control for higher speed nonmaneuvering targets[C]//2013 American Control Conference (ACC),Washington,DC,USA,June 17-19,2013:31-36. [10]In Soo Jeon,Jin Ik Lee.Optimality of proportional navigation based on nonlinear formulation[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(4):2051-2055. [11]Podlubny I.Fractional differential equations[M].San Diego: Acdamic Press,1999. [12]Y Q Chen,K L Moore.Discretization schemes for fractional-order differentiators and integrators[J].IEEE Trans On Circuits and Systems-I:Fundamental Theory and Applications,2002,49(3):363-367. [13]齐乃明,秦昌茂,宋志国.分数阶PI~λD~μ在高超声速飞行器姿态控制中的应用展望[J].航天控制,2010,28(5):93-98. [14]Necati Özdemir, Beyza BillurI skender.Fractional order control of fractional diffusion systems subject to input Hysteresis[J].Journal of Computational and Nonlinear Dynamics,2010,5:021002-1021002-5. [15]Yang Jie,Qi Dong-lian.The feedback control of fractional order unified chaotic system[J].Chinese Physics B,2010,19(2):020508-1-020508-4. [16]陈勇,赵惠昌,陈思,等.基于分数阶傅里叶变换的弹载SAR成像算法[J].物理学报,2014,11(63):118403-1-118403-9. [17]史金光, 王中原, 孙洪辉,等.制导炮弹分数阶控制器参数整定方法研究[J].战术导弹技术,2013(5):76-80. [18]王飞,雷虎民.基于分数阶微积分PD~λ比例导引制导规律[J].控制理论与应用,2010,27(1):127-130. [19]朱竹婷,廖增,彭程,等.一种分数阶修正比例导引律[J].控制理论与应用,2012,29(7):945-949. [20]张旭秀,邱天爽,盛虎.分数阶微积分的一种物理解释和定域长分数阶微积分[J].电子学报,2013,41(3):508-512. [21]侯明善,张金鹏.非线性比例导引系统研究[J].上海航天,2002(6):14-17. [22]Rituraj S,Prabhakar N,Sarkar A K,et al.Three dimensional nonlinear inverse dynamics guidance law for parallel navigation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Rhode Island.2004-4904:1-8. (编辑:吕耀辉) Novel 3D terminal guidance law based on the theory of fractional order calculus YE Ji-kun,WEI Dao-zhi,LI Jiong,SHAO Lei,LEI Hu-min (Air and Missile Defense College of Air Force Engineer University,Xi’an710051,China) A novel terminal guidance law based on the fractional calculus was derived aiming at intercepting the maneuvering target.Firstly,the definitions and properties of the fractional order calculus were introduced,the fractional order calculus proportional navigation(FOCPN)was proposed based on the traditional proportional navigation(PN) after analyzing the relative motion relation. Secondly, the characteristic of the load and the control effort of FOCPN were studied,and the trajectory stability of the FOCPN was researched through analyzing the change of leading angle,also the robust of FOCPN against autopilot parameters was analyzed by small deviator kinematics model.At last,simulation result shows that,compared with the traditional PN law,the new designed FOCPN has the higher guidance precision and the shorter intercept time,and it solves the problem of overload increasing sharply caused by divergence of line of sight rate.The new designed guidance law can intercept maneuvering target effectively. fractional calculus;guidance;proportional navigation;load;trajectory 2015-05-03; 2015-07-17。 国家高科技计划,航空科学基金项目(20130196004,20140196004)。 叶继坤(1984—),男,博士,研究方向为飞行器制导控制。E-mail:jikunbo@sina.com V448 A 1006-2793(2016)03-0428-08 10.7673/j.issn.1006-2793.2016.03.0262 FOCPN制导算法设计




3 FOCPN制导的弹道特性分析
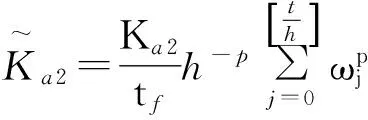

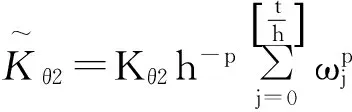

4 FOCPN制导鲁棒性能分析

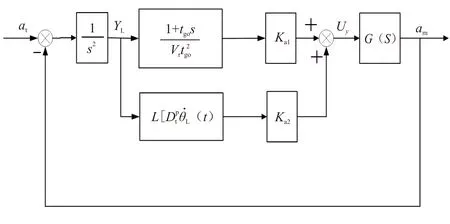
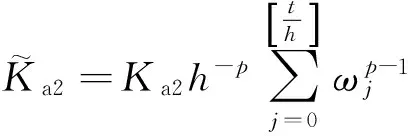

5 仿真分析




6 结论
