含夹杂的固体火箭发动机药柱应变场分析

孙　博，刘　忠，朵英贤，蒙上阳

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京　100081；2.中国航天科工集团061基地，遵义　365000；3.北京特种机电研究所，北京　100012)



含夹杂的固体火箭发动机药柱应变场分析

孙博1,3，刘忠2，朵英贤1，蒙上阳3

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京100081；2.中国航天科工集团061基地，遵义365000；3.北京特种机电研究所，北京100012)

为评估固体火箭发动机药柱含夹杂时的结构完整性，在无缺陷发动机结构完整性分析的基础上，在药柱应变梯度较大的部位设置了不同直径的夹杂，采用粘弹性三维有限元分析方法，获取了在常温、高温和低温点火发射时发动机药柱的应变场。结果表明，发动机药柱全局Von Mises应变最大值位于夹杂与推进剂界面上。通过计算含不同直径夹杂的药柱Von Mises应变场，得到夹杂区域最大Von Mises应变随夹杂直径的变化规律，并根据最大Von Mises应变准则，判断夹杂位于药柱不同位置时允许的最大直径。

固体火箭发动机；有限元方法；粘弹性；夹杂

0　引言

从严格意义上讲，固体火箭发动机都是含有缺陷的。目前，研究较多的有裂纹[1-2]、脱粘[3]和内聚空洞[4]等缺陷。在固体火箭发动机的生产和应用中，夹杂缺陷也是不可忽视的。发动机浇注时，生产工艺和生产经验表明，夹杂容易沉积于发动机的前中部。当发动机点火发射时，在发射载荷如环境温度、内压和轴向过载等载荷的作用下，由于夹杂和推进剂界面材料不连续，夹杂区域将出现应变极值。过高的应变可能会引发夹杂与推进剂界面区域萌生裂纹，裂纹失稳扩展容易导致发动机发生穿火、爆炸等灾难性后果。因此，含夹杂缺陷的固体火箭发动机在各种环境温度下点火发射时，确定不同位置夹杂允许的尺寸是发动机工程部门关注的问题。

以某型短圆柱-星孔药型结构的发动机为例，根据无缺陷发动机常温点火发射工况作用下的三维粘弹性有限元分析结果，确定发动机药柱前部应变极值部位，再将夹杂处理成球形颗粒，在发动机前部应变极值处，设置直径大小不同的球形夹杂，分别计算含夹杂缺陷的发动机药柱在常温(20 ℃)、高温(50 ℃)和低温(-40 ℃)点火发射时的Von Mises应变场，通过Von Mises应变准则，确定夹杂允许的最大直径。

1　粘弹性增量有限元方法

为更好地描述发动机推进剂、包覆层和绝热层材料的粘弹性特性，表征其蠕变和延迟弹性，需要采用积分型本构方程来描述，如由Boltzmann叠加原理所得的积分型本构关系[4-5]：

其中

(2)

(3)

(4)

(5)

式中E(0)为初始模量(t=0)；αT为热膨胀系数；T为相对温度变化；ν为泊松比。

为解决积分函数需要全历程积分求解的不便，有限元法中采用增量型本构关系克服这一困难，粘弹性材料的松弛模量E(t)可表述成Prony级数形式：

(6)

式中E∞为t→∞时的长期模量；En为第n个Maxwell单元的弹性模量；τn为松弛时间。

将式(1)积分型本构关系在时域中离散，即将[0,t]时间区间离散成N个步长为h=tm-tm-1时间段，可得增量型的本构关系：

(7)

其中

(8)

(9)

(10)

(11)

(12)

(13)

由虚功原理，得到虚功方程增量形式：

(14)

式中{δu}为虚位移；{δε}为虚应变；{ΔP}为增量面力或增量集中力；{Δp}为增量体力。

将式(7)代入式(14)，有

(15)

得总体平衡方程：

(16)

其中

(17)

(18)

(19)

发动机推进剂、包覆层和绝热层材料属于热流变简单材料，可由时间-温度等效，将时间t用等效时间ξ代替即可，关系为

(20)

其中，aT为时间-温度等效因子，由WLF方程确定：

(21)

式中C1、C2为材料常数；T0为参考温度；T为环境温度。

2　发动机药柱有限元模型

图1为某型短圆柱-星孔药型发动机的三维有限元模型及构成材料图，发动机承受的环境温度、内压和轴向过载为轴对称性载荷，发动机药柱为循环对称性结构，取其中循环对称的一份1/12建立模型，共划分了125 831个六面体单元，节点总数为146 872个。

(b)发动机1/2模型

根据模型的循环对称性，约束对称剖面的环向位移，壳体两端为位移简支。发动机的绝热层、包覆层和推进剂材料在各温度下的松弛模量可通过试验测取，并拟合成Prony级数，有

(22)

式(21)的时间-温度等效参数C1取17.3、C2取367.5。不同发射工况时发动机材料的泊松比、内压峰值和轴向过载的值如表1所示，发动机增压至峰值时间为40 ms。

表1　不同工况下发动机材料参数及载荷

常温点火发射时，无缺陷发动机的Von Mises应变场等值线分布如图2所示。在翼槽一侧的对称面应变相对较大，选择在该侧面设置夹杂，设置原则是考虑夹杂相对靠近发动机前端、应变及应变梯度相对较大的区域。取药柱前段应变及其梯度较大处作为第Ⅰ个预设位置，药柱中段应变及其梯度较大为第Ⅱ个预设位置，过渡段应变梯度较大部位为第Ⅲ个预设夹杂区域。

图2　发动机常温点火发射时药柱Von Mises应变场等值线图及夹杂设置区域

如图3所示，以预设夹杂直径为6.0 mm为例。图3(a)为预设部位无夹杂的有限元模型，图3(b)为设置夹杂后的有限元计算模型图，图3(c)为夹杂的三维有限元模型示意图。根据对称性可知，相当于在整个发动机中含有6个夹杂，由于发动机全局尺寸远大于夹杂的尺寸，由圣维南原理可知，夹杂之间的应力应变不会耦合。别外，夹杂引起的应力应变突变主要是由于夹杂处材料不连续引起的，以夹杂材料模量为推进剂一半(其他力学性能参数相同)为例进行分析。

(a) 未设置夹杂　(b) 设置夹杂后　(c) 设置夹杂三维模型

3　含夹杂发动机药柱的Von Mises应变场分析

3.1药柱前段夹杂区域的Von Mises应变场

如图2所示，将夹杂的圆心设在发动机前部的应变等值线8和9之间，分别预设不同直径的夹杂，通过计算可得到对应的Von Mises应变场分布情况。图4所示为夹杂直径为6.0 mm时，夹杂附近区域的Von Mises应变场等值线图。结果可见，夹杂与推进剂界面区域的Von Mises应变为全局最大，相比无缺陷发动机药柱的Von Mises应变场，全局的最大Von Mises应变值转移至夹杂区域，且夹杂区域的Von Mises应变分布在夹杂直径约1倍的圆域内。

为探讨高温、常温和低温发射时，发动机药柱前段夹杂最大Von Mises应变值与夹杂尺寸之间的关系，用曲线表征夹杂尺寸(直径)与其最大Von Mises应变值的变化规律，即得夹杂区域Von Mises应变-夹杂直径曲线。如图5所示，为夹杂存在于发动机药柱前段应变极值区域时，夹杂区域Von Mises应变极值随夹杂直径的变化规律。

(a)夹杂局部模型(b)Von Mises应变场等值线图

图4常温发射药柱中段夹杂直径6.0 mm时的Von Mises应变等值线图

Fig.4Von Mises strain contour of the first regional impurity with 6.0 mm diameter

结果表明，只要存在直径为4.0 mm的夹杂，发动机全局最大Von Mises应变即位于夹杂与推进剂界面处。从图5可知，随着夹杂直径增加，夹杂处的Von Mises应变增加，而高温点火发射时较常温和低温点火发射的增速略快些。发动机推进剂常温、高温和低温的许用Von Mises应变同样分别为35%、40%和32%。由图5可知，常温点火发射时，药柱前段的夹杂直径不能超过18.5 mm；高温点火发射时，药柱前段的夹杂直径不能超过19.0 mm；而低温点火发射时，药柱前段的夹杂直径不能超过11.0 mm。即该型发动机在使用环境下，药柱前段的夹杂不能超过11.0 mm，在发动机出厂和贮存检测时，若发现存在夹杂现象，注意定位夹杂的形状、位置及材料性质，可通过数值方法对夹杂的安全性进行评估，确定该部位允许的最大夹杂尺寸。

图5　点火发射时药柱前段夹杂直径与最大Von Mises应变的关系

3.2药柱中段夹杂区域的Von Mises应变场

如图2所示，在发动机药柱中段的应变等值线0和A之间设置夹杂。图6所示为常温发射时，夹杂直径为10.0 mm时的应变场等值线图。可知，夹杂区域的Von Mises应变值为发动机全局最大，由于在内压作用下，整个药柱是三向受压状态，不仅压应力很大，而且径向压应力较环向和轴向压应力大。所以，最大应变产生于夹杂与推进剂的材料不连续区域。图7所示为高温、常温和低温点火发射时中段夹杂最大Von Mises应变值与其对应夹杂的直径变化规律。

由图7可知，常温点火发射时，药柱中段的夹杂直径不能超过14.5 mm；高温点火发射时，不能超过19.0 mm；而低温点火发射时，药柱中段的夹杂直径不能超过12.5 mm。因此，该型发动机在药柱中段的夹杂直径不能超过12.5 mm。

图6　常温发射药柱中段夹杂直径10.0 mm时Von Misses应变场等值线图

图7　药柱中段夹杂直径与最大Von Mises应变的关系

3.3药柱过渡段夹杂区域的Von Mises应变场

为探讨发动机过渡段区域存在夹杂的应变场分布情况，如图2所示，在发动机药柱过渡段区域的应变等值线9和10之间设置夹杂，图8所示为夹杂直径为6.0 mm时的应变场等值线图。

图9所示为发动机分别在常温、高温和低温环境温度下点火发射时，药柱过渡段含夹杂的最大Von Mises应变值与对应夹杂直径的变化规律。

计算表明，夹杂导致发动机全局最大Von Mises应变由圆柱段中部转移至夹杂处。从图9可知，随着夹杂直径由6.0 mm增至20.0 mm，夹杂里的Von Mises应变随直径增加而增加，与发动机前段及中段含夹杂时的Von Mises应变分布相似。

图8 常温发射药柱过渡段夹杂直径6．0 mm 时Von Mises应变等值线图

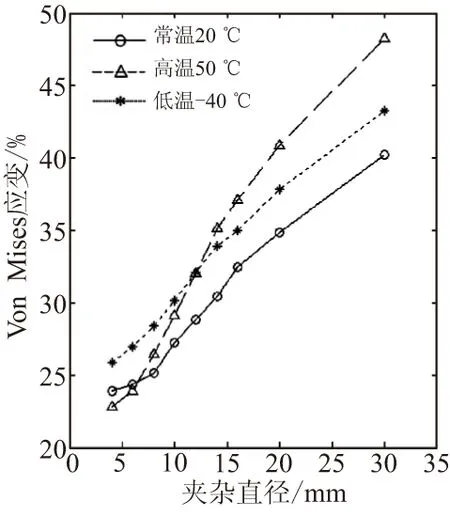
图9　药柱过渡段夹杂直径与最大Von Mises应变的关系

由图9可知，常温点火发射时，药柱过渡段的夹杂直径不能超过20.0 mm；高温点火发射时，不能超过19.0 mm；而低温点火发射时，药柱过渡段的夹杂直径不能超过13.0 mm。因此，该型发动机在药柱过渡段的夹杂直径不能超过13.0 mm。

4　结论

(1)发动机分别在常温、高温和低温环境温度下

点火发射时，在夹杂与推进剂界面区域产生很大的Von Mises应变极值，过大尺寸的夹杂可能导致发动机结构完整性的破坏。数值计算结果表明，3种环境温度下点火发射时，夹杂区域Von Mises应变极值与夹杂直径呈正比增加。药柱前段允许的夹杂最大直径为11.0 mm，中段为12.5 mm，药柱过渡段为13.0 mm。可见，前段的夹杂最大Von Mises应变值比药柱中部和过渡段大，主要原因是该部位的三向应力值和应变梯度均较大。另外，发动机药柱夹杂最大允许尺寸均由低温点火发射决定，表明低温发射是发动机使用最为危险的情况。

(2)在固体火箭发动机的生产中，应加强推进剂原材料质量控制，尽可能减少发动机浇注时混入杂质；同时，加强成品发动机检测，对出现夹杂缺陷的发动机需要确定夹杂形状、位置及材料性质，采用数值方法评估含夹杂发动机的结构完整性，为含夹杂缺陷发动机的判废提供量化参考。

[1]徐学文,孙建国,牟俊林.某固体火箭发动机药柱上三维裂纹扩展的判定[J].固体火箭技术,2008,31(4):331-335.

[2]Han Bo,Ju Yu-tao,Zhou Chang-sheng.Simulation of crack propagation in HTPB propellant using cohesive zone model[J].Engineering Failure Analysis,2012(26):304-317.

[3]许萌萌,胡春波,何国强.固体火箭发动机界面脱粘裂纹分析[J].固体火箭技术,2008,31(2):121-124.

[4]蒙上阳,唐国金,袁端才,等.含内聚空洞的固体火箭发动机药柱结构完整性分析[J].暨南大学学报,2005,26(1):64-68.

[5]蒙上阳,李荣,沈先锋,等.固体火箭发动机药柱主动段飞行时应力、应变分析[J].固体火箭技术,2008,31(5):466-470.

[6]杨挺青,罗文波,徐平,等.粘弹性理论与应用[M].科学出版社,2004.

(编辑：薛永利)

Strain field analysis of solid rocket motor grain with impurity

SUN Bo1,3, LIU Zhong2, DUO Ying-xian1, MENG Shang-yang3

(1: State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing100081, China; 2: The 061 Base of China Aerospace Science and Industry Company, Zunyi356000, China; 3: Beijing Institute of Special Electromechanical Technology, Beijing100012, China)

In order to evaluate the structure integrity of solid rocket motor(SRM) grain with impurity,based on the structure integrity analysis of perfect SRM grain,some positions were determined to preset impurities in different strain grads of the SRM grain.The three-dimension viscoelastic finite element models of the SRM grain with impurity were established.The strain fields of the grain with impurity were studied respectively when it was launched under normal temperature, high temperature and low temperature.The results show that these impurities would cause serious strain concentrations at the interface between the grain and impurity.The maximum Von Mises strain of different regions and different diameter impurities were obtained.Then the allowable maximum diameter of the impurity could be determined by the maximum Von Mises strain criterion.

solid rocket motor;finite element method;viscoelasticity;impurity

2014-12-01；

2015-01-06。

国防预研支撑项目(No.40403)。

孙博(1975—),女,博士,研究方向为固体火箭发动机结构完整性和断裂损伤。E-mail:sunbo5536@163.com

V435

A

1006-2793(2016)02-0174-05

10.7673/j.issn.1006-2793.2016.02.004