几种常用基坑变形预测模型的比较与分析

王 兴

（山西省勘察设计研究院，山西太原030013）

几种常用基坑变形预测模型的比较与分析

王 兴

（山西省勘察设计研究院，山西太原030013）

文章分析了目前常用基坑变形预测模型的特点和不足，通过应用卡尔曼滤波模型对状态向量进行滤波，构建了一种新的基于卡尔曼滤波的动态回归模型，并结合各种模型在工程实例中的表现，经过比较和分析得到了一些有益的结论。

变形监测；基坑；卡尔曼滤波；预测模型

基坑的变形预测是基坑变形监测中的意义最为重要的工作，将预测值与最近一期测量结果相比较，以判别上一步施工工艺和施工参数是否对基坑安全造成影响以及优化下一步施工参数，进而指导现场施工。

1 目前常用的基坑变形预测方法

1.1 传统模型数值分析

传统的回归分析预测模型虽然简单实用,但由于不便于描述系统变化过程及其内在规律，只局限于用差分方程来建立离散的随机模型。数值法在数学方法上相对精确,但由于基坑边坡影响因素的多样性、复杂性、模糊性以及不确定性,使得在使用该方法时过分概化,降低了实用价值,预测结果的实用性和可靠性相对较低[1]。

1.2 灰色系统

灰色系统理论，原理就是从乱的数据中发现内在的规律，研究对象是规律性比较强的生成数列。数列生成使用的方法是概率统计法和数据生成法，通过这两种方法，将系统内的随机数据整理成规律性较强的数据。基坑变形预测的理论基础就是这一灰色系统理论，通过建立一个基坑位移灰色预测模型预测基坑的变形趋势。灰色预测模型的缺点是：想要找到合适的微分方程进行拟合就要求累加生成的数列满足灰色指数规律。然而，有些时间序列的累加序列有时也满足近似指数规律，这就需要利用残差序列模型对拟合数据进加以修正，这种做法会将误差向反方向扩大。

1.3 神经网络预测

对人脑神经元网络进行分析研究，抽象出的某种网络模型，即为人工神经网络，也可称为神经网络或类神经网络。神经网络由大量的节点，即神经元相互连接构成。节点被称为激励函数，即输出函数。节点间的连接被称为权重，即通过该连接信号的加权值。激励函数与加权值的共同作用即为人工神经网络的记忆。同时，人工神经网络的输出又主要依托于加权值和激励函数，加权值和激励函数的不同会影响人工神经网络的输出。人工神经网络的记忆和人工神经网络的输出共同构成神经网络，这是一种对自然界某种算法的逼近，是一种运算模型。

神经网络具有非线性、非局限性、非常定性和非凸性的基本特征，这就要求必须通过大量的学习样本来对网络进行训练。当学习样本较少，训练次数不足时，预测精度就比较差。在基坑变形监测初期，监测数据较少的情况下，不应选用这种模型进行变形预测。

1.4 时间序列分析

时间序列分析的方法认为逐次的观测值通常不是独立的，数据内部一定存在着某种特定的关系，且考虑到观测资料的时间顺序。当逐次观测值相关时，可以通过过去观测资料来预测未来数值，同时可以利用观测数据之间的这种特定关系建立相应的数学模型来描述数据所反映的变形体的变形特性[2]。

时间序列的建模预报思路,分为三步：

第一步，变形位移数据的预处理和检验。通过差分对数据进行预处理，预处理之前剔除掉个别与大量数据偏差较大的点的位移数据，使数据能够进行平稳性检验。

第二步，模型参数估计。首先采用最小二乘法计算得到初值,然后利用第一步获得的预处理数据,再次采用最小二乘递推法，计算出新的估计模型参数。

第三步，预报。按照第二步得出的估计模型参数对基坑变形的位移量进行预测计算，然后利用新获得的变形数据信息估计出新的模型参数,继续进行下一步的预测,如此反复递推，就能预测基坑的变形,并对其状态和发展趋势有比较精确的预判。

时间序列分析在剔除影响观测值的各种力学因素的前提下只分析观测数据的统计规律性，缺乏对变形体物理意义上的把握，并且其外推时间不宜过长，在应用时必须参考其他方法进行相互之间的校正,以确保基坑预测数据的准确性，以及基坑围护的可靠性和安全性。

2 基于卡尔曼滤波的回归模型的构建

基于卡尔曼滤波的回归模型的基本思想是在监测数据与监测期数之间建立一个回归模型，将卡尔曼滤波回归模型的模型参数作为状态向量，应用卡尔曼滤波模型对状态向量进行滤波，利用最新的模型参数滤波值对回归模型进行修正，构建一种基于卡尔曼滤波的动态回归模型[3-5]。

首先利用MATLAB软件对监测数据进行处理，根据剩余标准差最小原则，得到的回归模型为：

式中，S为建筑物累计沉降量，mm；t为观测期数，d；ai为模型系数，i=1，2，3，4。

根据基于卡尔曼滤波的回归模型的构建思想，将式（1）中的模型参数看作状态向量，建立监测点回归模型参数的卡尔曼滤波模型，以便增强模型的适应性[6-7]。其模型为：

式中，t为观测期数，d；St为t时刻监测点的累计变形量；Δt为t时刻的观测噪声。

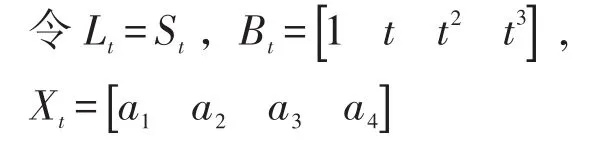
则式（2）变为：

式（3）为卡尔曼滤波模型的观测方程。为了便于卡尔曼滤波，将其看作包含有动态噪声的状态向量，则有：

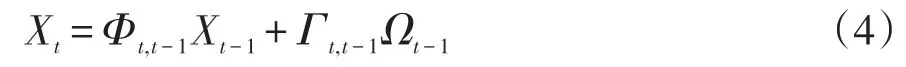
式中，Φk,k-1为k-1到k时刻的系统一步状态转移矩阵；Γk,k-1为系统噪声矩阵。

根据式（3）和式（4），则有卡尔曼滤波法的状态方程和观测方程：

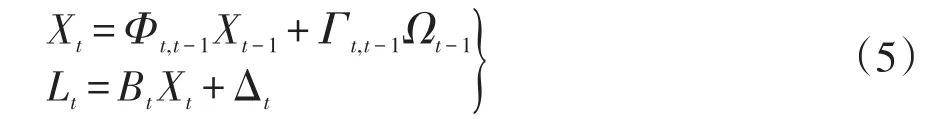
式（1）和式（5）即为基于卡尔曼滤波的回归模型。

3 实例分析

某项目基坑总长237.6 m，宽33.8 m，底板埋深20.8 m，围护采用直径800 mm地下连续墙，嵌入深度约19.5 m。基坑西侧有一座正在使用的6层住宅楼，为了确保基坑开挖过程中周边建筑物的安全，2012年10月20日在该建筑物上增加沉降监测点8个，监测频率为2次∕天，现选用2012年10月20日至2012年12月20日监测点沉降数据进行分析。沉降观测数据，见表1。

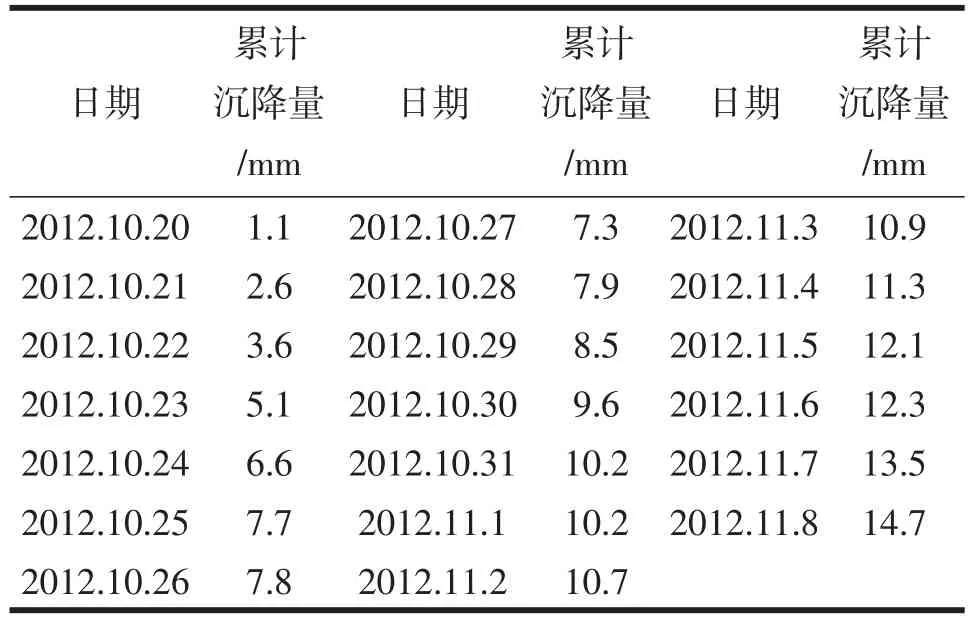
表1 沉降观测数据

根据本文思想，分别建立回归模型（模型Ⅰ），基于卡尔曼滤波的回归模型（模型Ⅱ），灰色预测GM(1,1)模型（模型Ⅲ），时间序列模型（模型Ⅳ），神经网络模型（模型Ⅴ）。

1）模型Ⅰ

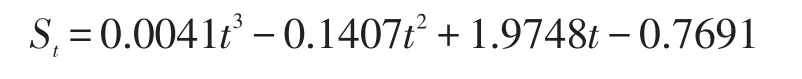
2）模型Ⅱ

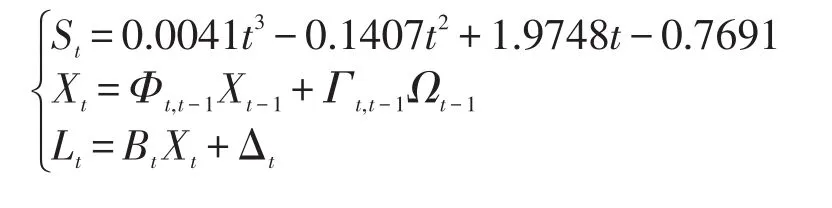
建立模型Ⅱ时，卡尔曼滤波初值为：

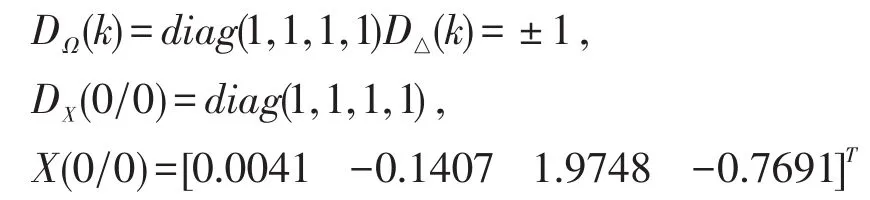
3）模型Ⅲ

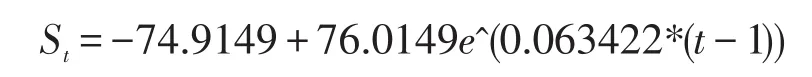
4）模型Ⅳ

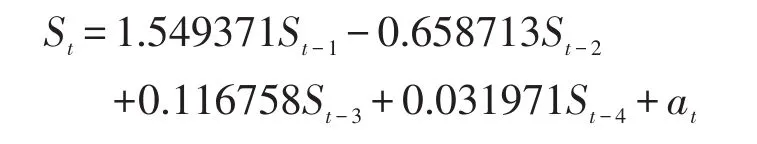
式中，t为观测期数，d；at为白噪声。

5）模型Ⅴ

应用Elman神经网络建立残差修正模型，其网络结构为3×10×1，训练步长设为100 000，训练误差设为0.01，学习系数设为0.1。

用上述五种模型对10月20号到11月5号的监测数据进行拟合，并对11月6号到11月8号的监测数据进行预测，分析结果，见表2。五种模型拟合值对比图，见图1。五种模型预测残差值对比图，见图2。

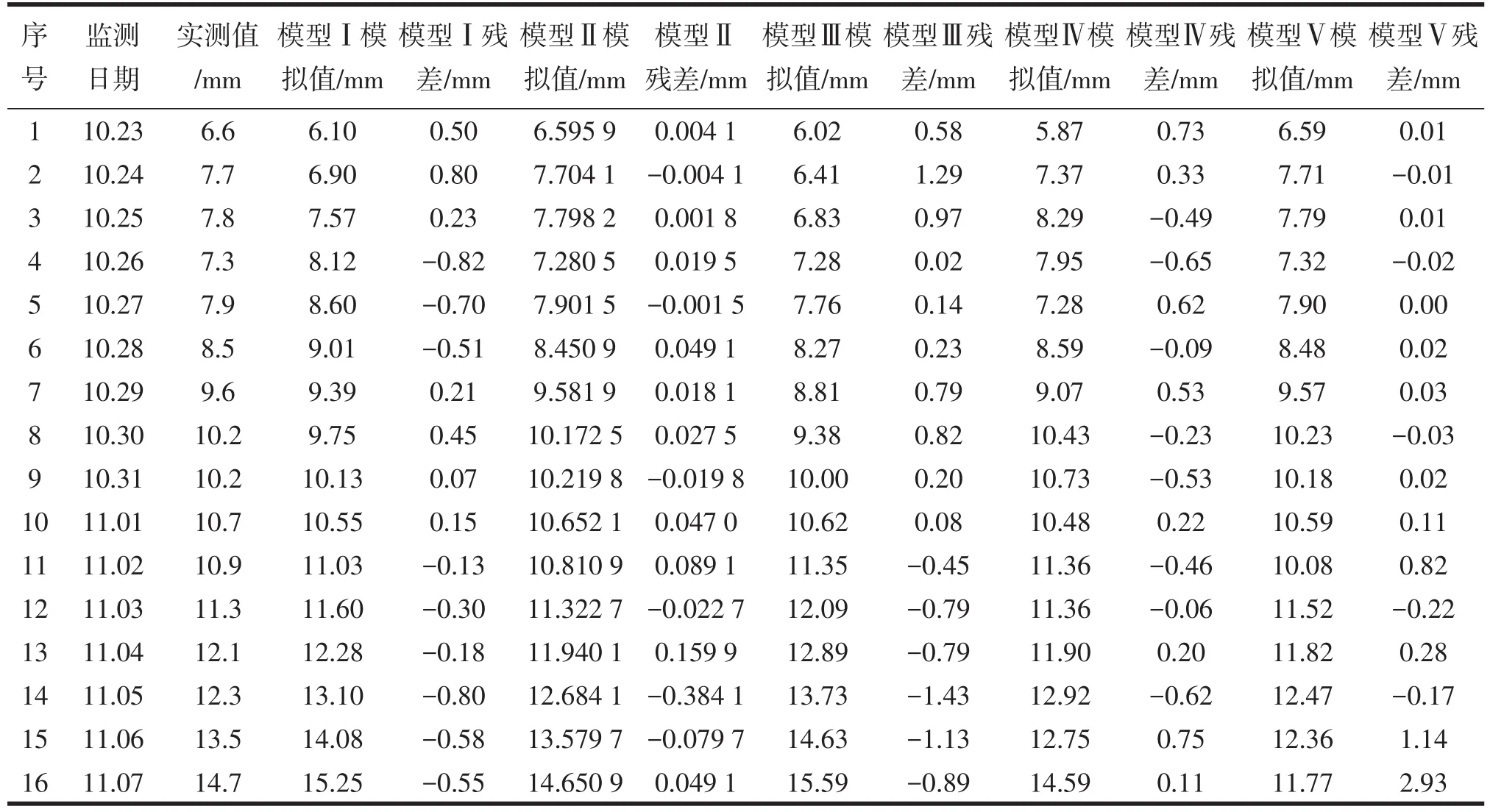
表2 沉降数据分析结果

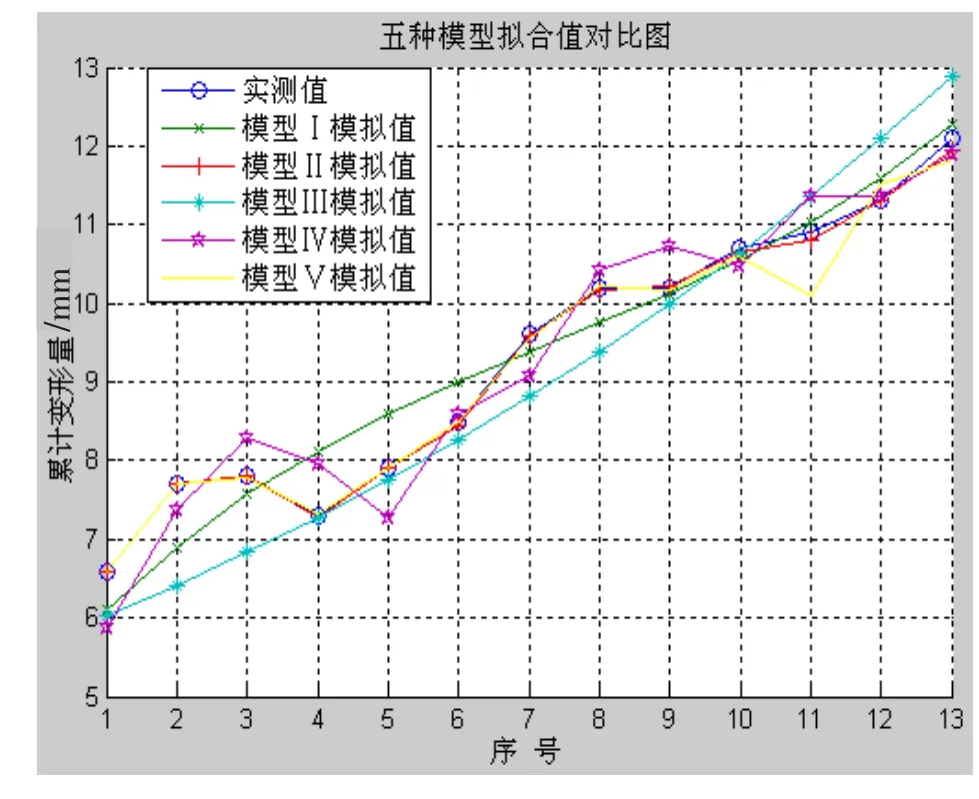
图1 五种模型拟合值对比

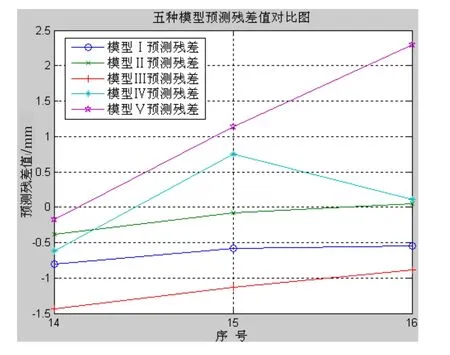
图2 五种模型预测残差值对比

从分析结果可以看出，本文建立的基于卡尔曼滤波的回归模型模拟残差和预测残差都最小，说明模型Ⅱ的建模精度非常高，而且预测误差均小于0.5 mm，预测效果较为理想；模型Ⅴ的预测精度最差，这主要是由于神经网络建模需要大量的训练样本，而本文的训练样本不足造成的。

4 结论

（1）本文建立的基于卡尔曼滤波回归模型是将回归模型的模型参数看作状态向量建立的卡尔曼滤波模型，为增强模型对变形观测数据预测的能力，在滤波过程中，将模型的参数不断变化，旨在提高基坑监测数据的模拟精度，从而为基坑监测数据的预判提供更好的理论基础。当有新增观测数据时，要及时更新数据对模型参数进行滤波。

（2）在基坑监测初期，由于缺少足够的训练样本，不宜选用神经网络模型对监测数据进行处理。

（3）当监测数据具有灰色指数特性时，宜选用灰色模型。当监测数据之间具有较强的相关性时，宜选用时间序列模型。当具有大量的监测数据时，宜选用神经网络模型。当不能确定选用何种模型时，可以同时应用多种模型处理数据，根据模拟精度和预测精度从中选择最优的模型。

[1]范建,师旭超.深基坑变形预测方法综述[J].西部探矿工程，2006,18(4)：29-31.

[2]钟正雄,杨林德,杨金松.基坑变形的实时建模预报时序分析方法[J].工业建筑,2000,30(3)：1-3,42.

[3]王平卫,彭振斌,何忠明.基于灰色理论的基坑变形预测[J].地质与勘探,2006,42(6)：94-97.

[4]李德仁,袁修孝.误差处理与可靠性理论[M].武汉：武汉大学出版社，2002.

[5]刘大杰,陶本藻.实用测量数据处理方法[M].北京：测绘出版社，2000.

[6]陆付民.顾及多个因子的卡尔曼滤波法在大坝变形分析中的应用[J].水电自动化与大坝监测,2003,27(3)：71-73.

[7]陆付民.顾及时间和水位因子的卡尔曼滤波法在大坝变形分析中的应用[J].三峡大学学报：自然科学版，2004,26(5)：392-394,436.

The Comparison and Analysis of Several Deformation Forecast Models of Pit

WANG Xing
（Shanxi Investigation Research and Design Institute，Taiyuan Shanxi,030013）

On the basis of analyzing the advantages and disadvantages of the current prediction model of pit deformation and establishing the regression model between monitoring data and monitoring number in this paper,the model parameter is regarded as a state vector.And with the application of kalman filter model to the state vector for filtering and the latest state vector to regression model for amending,a dynamic regression model based on kalman filter model is established.Some useful conclusions are got through the comparison and analysis of several models in an engineering example.

deformation analysis;pit;Kalman filter;prediction model

TU191+.1

A

1674-0874(2016)01-0062-04

2015-10-09

王兴(1983-)，男，山西吕梁人，注册测绘师，研究方向：变形测量。

〔责任编辑 王东〕