基于ISIGHT平台的大型空间望远镜主镜主动光学系统研究

张立浩，张远清，董吉洪，孙阳

（中国科学院长春光学精密机械与物理研究所，长春　130033）

基于ISIGHT平台的大型空间望远镜主镜主动光学系统研究

张立浩，张远清，董吉洪，孙阳

（中国科学院长春光学精密机械与物理研究所，长春130033）

为了实现大型空间望远镜的高成像质量，建立了主镜主动光学系统模型。对主镜面形校正的算法、主镜面形校正的精度以及主镜面形校正能力等进行研究。首先，对主镜面形校正的算法进行研究。对主镜的镜体结构和支撑方案进行设计，建立了主镜有限元模型。构造了单位主动力矩阵和主镜面形响应矩阵。采用广义逆矩阵法求得了主镜面形校正矩阵。接着，采用多学科分析平台Isight建立主镜面形校正精度模型，以慧差为例，分析了主镜面形校正的准确性。最后，采用Isight平台建立了主镜面形校正能力分析模型，以低阶像散为例，分析了在促动器最大调整力为100N时，主镜面形的校正能力。分析结果表明：主镜慧差的校正精度为4%；力促动器能校正0.467个波长的像散。主镜面形校正算法及模型基本准确，可用来进行主镜面形校正。

主镜；主动光学；Isight平台；面形校正

传统望远镜往往采用刚度很大的主镜、膨胀系数近于零的镜面材料、复杂的镜面支撑系统等，以使望远镜维持较好的光学面形和准直。这些措施往往造价很高或技术难度高，而效果却很有限，望远镜的像质仍然不够理想。对大口径望远镜而言造价高且像质差的问题就尤其严重。

图1　主镜面形校正算法

20世纪70年代到80年代，在望远镜研制中发展并逐渐成熟了一种新技术，它的基本思想是实时检测望远镜的像质或镜面形状，实时作校正，使望远镜始终保持优秀的像质，这种技术称为主动光学（Active optics）。按主镜的结构可将主动光学分为镜面主动光学和拼接镜面主动光学两大类。镜面主动光学的代表是ESO的VLT，VLT主镜材料为Zerodur，口径8.2m，厚17.5cm，背面有150个力促动器。波前传感器将采集的数据送入计算机，计算机解算波面误差，控制系统根据波面误差解算的力促动器应施加的主动力，并据此来校正这些误差［1-6］。拼接镜面主动光学的代表是美国Keck 10m望远镜。Keck主镜由36块六角形子镜拼成，每块对角线长1.8m，厚75mm，每个子镜采用主动支撑来共同校正误差［7-10］。

本文主要是对某大型天文望远镜的主镜镜面主动光学进行研究，主要分为以下几部分：主镜面形校正算法研究、主镜面形校正精度分析和主镜面形校正能力研究。

1　主镜面形校正算法研究

主镜面形校正算法主要包含主镜面形校正模型，面形计算，面形结果的拟合与像差分解和面形校正主动力求解共四个部分。为了能实现较好主镜面形校正结果，首先要建立主镜面形校正模型。主镜面形校正模型包括轻量化的镜体设计，实现定位的支撑设计，以及合理的主动光学促动器数量和分布的设计。根据设计完成的主镜模型，建立有限元模型，并计算主镜面形值。从仿真分析结果中提取出主镜的面形数据，进行原始面形拟合，确定面形误差。对面形结果进行像差求解，并对面形进行Zernike展开，分解出前18阶像差。采用波面拟合的Zernike多项式相互正交，相互独立，根据正交定律，可分别对每个像差加以校正而不产生相互之间的影响。通过主镜面形与主动力之间的响应矩阵求解，得到不同像差的面形校正所需的主动力。将主动力施加到主镜的有限元模型当中，即可实现主镜的面形校正。对主动力校正后得到面形数据再次进行像差求解，Zernike展开，校正所需主动力求解与加载，反复迭代，直到仿真分析所得的主镜面形结果满足设计需求，停止迭代，完成主镜面形校正，基本算法如图1所示。本文主要对主镜面形校正模型和主镜面形校正矩阵进行研究。

1.1主镜及支撑模型

本文研究的主镜通光孔径为2.4m，镜体材料是碳化硅。主镜采用轴向被动支撑及轴向主动支撑混合支撑方案。轴向支撑采用三点固定支撑方式，三支撑点为镜面空间位置进行定位。三硬点的位置呈120度均匀分布，具体径向位置选择为主镜半径的0.6倍。主动支撑采用基于力控制的促动器。促动器的数量与排布方式对主镜的镜面响应函数产生直接的影响，是决定主镜面形校正性能的重要参数。从理论上分析，变形镜的控制促动自由度数量不能少于待校正的目标像差的数量。而要在空间相机中应用，促动器数量应在满足校正精度的同时，尽量的少。根据主镜重力变形值最小和促动器力平衡与力矩平衡的设计原则来设计促动器的点数以及分布，初步设计结果为36个促动器，呈六边形排布，六边形排布具有更加对称的镜面响应函数。36个主动支撑点分为六组，这六组呈60度均匀分布。每组的六个点组成一个等边三角形，这六个点分别位于等边三角形的顶点和边的中点上，等边三角形的高选择为主镜半径的0.6倍。主镜支撑点的设计结果如图2所示。

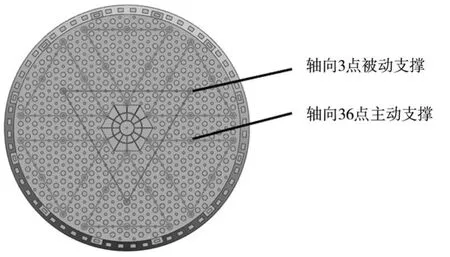
图2　主镜镜体结构及支撑方案

采用大型有限元分析软件Abaqus建立主镜的有限元模型，如图3所示。采用Tet10单元对主镜进行有限元网格划分；对3硬点位置施加约束边界条件；在主镜36点主动支撑处建立36个主动力，用来进行面形校正。

图3　主镜组件有限元模型

1.2主镜面形校正矩阵研究

为了获得面形主镜校正所需要的主动力，先要求解得到主镜面形与促动器主动力的响应矩阵。主镜的材料符合Hooke线性定律，主镜的镜面变形符合力的线性叠加。在主镜模型上每个促动器上分别施加单位力，计算每个促动器单独工作时的主镜面形响应。36个单位主动力构成了单位主动力矩阵，其面形响应结果构成了面形响应矩阵，通过响应函数求解，可以得到主镜面形校正矩阵。面形校正矩阵的求解流程如图4所示。

依据面形与主动力响应矩阵求解流程，在多学科分析软件Isight平台上分别建立主动力输入表，主镜有限元分析模块，面形数据输出模块，面形校正矩阵求解程序，如图5所示。

图4　面形校正矩阵求解流程

图5　面形校正矩阵解算模型

首先利用Isight平台下的EXCEL模块建立主动力输入表。主镜的主动支撑为36个促动器，在面形校正矩阵求解时每个促动器的输入力都是1N。建立了一个36*1的表格，每个表格的数据都是1，每个表格数据与主镜有限元模型中的主动力进行数据连接。这种建模方式的优点就是有限元仿真模型中的主动力实现可交互性，方便修改主动力的输入参数，可以实现自动化的有限元模型数据修改与载荷施加。

利用Isight平台下的Abaqus模块导入主镜有限元模型，对主镜在促动器安装点分别建立加载工况，每个促动器加载工况下的载荷与前一个主动输入表的载荷关联，进行仿真分析，得到每个单位力作用下的主镜面形结果，部分结果如图6所示。

图6　单位主动力面形响应结果

由于主镜镜面上的节点数目较多，如果选择所有镜面节点进行面形校正矩阵求解，运算量大，同时求解结果可能奇异，故在镜面上均匀了选择了三圈节点（共123个），输出这些节点的位移值，用来进行面形校正矩阵求解。为了实现节点位移输出的自动化，编写节点位移输出的宏命令，利用利用Isight平台下的Simcode模块自动运行，自动输出每个载荷工况的主镜面形变化值。

根据上面得到的促动器主动力值与主镜面形值，求解面形校正矩阵。假设每个促动器对面形的影响是正交的，构造主动力矩阵为36*36的单位矩阵。每个主动力工况下的面形矩阵是一个123*1的矩阵，根据主动力的构造顺序，把36个工况下的面形矩阵合成一个123*36的矩阵。主动力和面形的关系可以如下式表示，其中K矩阵即为面形校正矩阵，是一个36*123的矩阵。

通过对上式进行广义逆矩阵求解，可以得到面形校正矩阵K

利用利用Isight平台下的Matlab模块建立面形校正矩阵求解模块。编写Matlab程序进行数据读取，构造面形矩阵和主动力矩阵，利用广义逆矩阵法得到了面形校正矩阵K，并输出K的结果，提供给主镜校正精度分析和校正能力分析时使用。矩阵K的部分结果见表1。

2　主镜面形校正精度分析

主镜面形校正精度分析的基本方法是首先设定主镜的像差，根据Zernike系数中的像差系数计算主镜校正目标的面形值；然后根据面形校正矩阵求得预定面形下的促动器主动力；通过有限元仿真分析得到主动力施加后的主镜面形；最后对预定面形和校正面形进行分析，得到面形校正的准确性。依据面形校正精度分析流程，在多学科分析软件Isight平台上分别建立预定面形计算程序和主动力求解程序，主镜有限元分析模块，面形数据输出模块，精度分析程序，如图7所示。

图7　面形校正精度分析模型

本节主要以慧差面形为例，分析主镜的面形校正精度。Zernike系数中y向的慧差项为（3ρ3-2ρ）*sinθ。根据面形坐标数据，把其转换成极坐标系，初选像差幅值为0.5λ，λ=632.8nm，利用Matlab编写预定面形计算程序，可以计算得到慧差的面形值见表2。

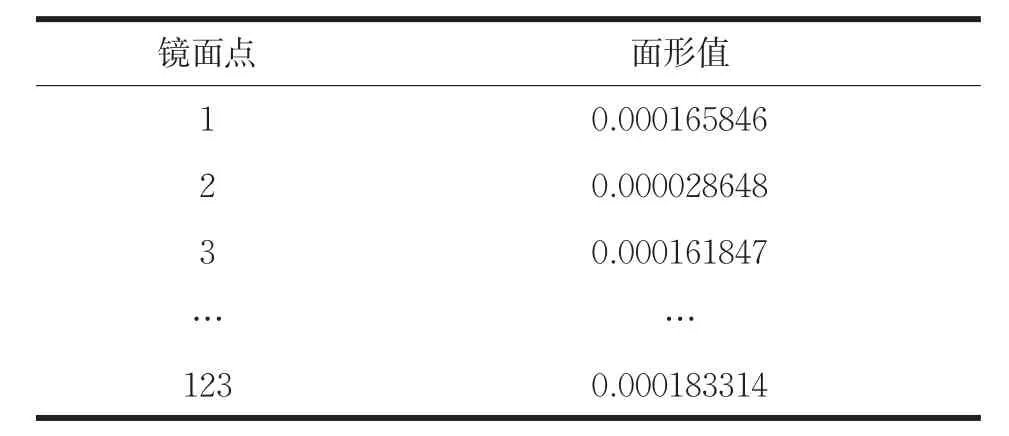
表2　慧差面形值

利用Isight平台下的Matlab模块建立面形校正矩阵求解模块，得到面形校正矩阵K。面形校正矩阵K与慧差面形矩阵X相乘，可以计算得到面形校正所需主动力的值，见表3所示。

表3　慧差校正主动力值

利用Isight平台下的Matlab模块建立精度分析程序，对比分析校正面形值与与预定面形值的结果，分析结果见表4。从表中可以看出慧差面形校正时，有一些主镜镜面上的点校正效果较好，误差率为1%以内；有一些位置校正误差达到了8.58%。面形校正误差大可能与主镜镜面节点的选取原则，刚度矩阵求解精度，以及主镜慧差校正能力有关。

表4　慧差面形校正精度

3　主镜面形校正能力分析

根据促动器的数量和分布以及促动器的调整能力，可以分析出整个主动光学系统的不同像差的主镜面形校正能力。本节以促动器行程为±100N前提下，分析了主镜的面形校正能力。在主镜面形校正精度分析模型的基础上，增加主动力优化模块，如图8所示。初步选定低阶像散作为预定像差，初选0.5个波长的像差，根据Zernike系数中的像差系数计算主镜校正目标的面形值；通过面形校正矩阵求得主动力，以促动器的最大校正力100N为优化目标进行优化，得到主镜面形校正系统的像散的最大校正能力。

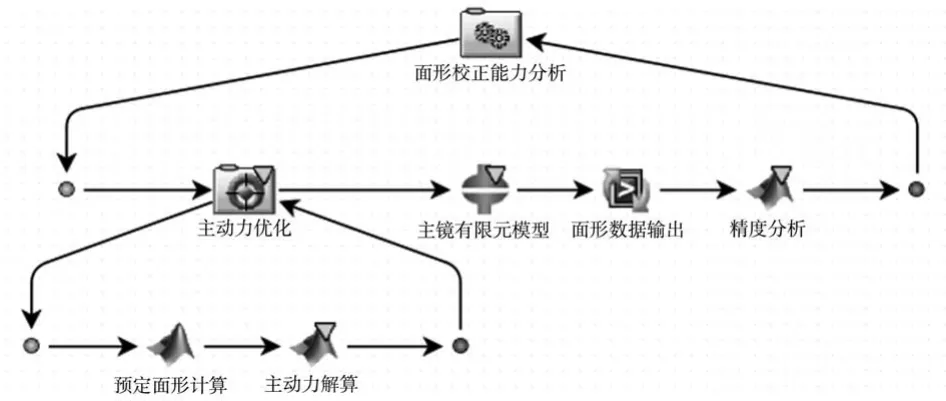
图8　面形校正能力分析

Zernike系数中的像散项为ρ2*sin2θ。根据面形坐标数据，把其转换成极坐标系，初选像差幅值为0.5λ，λ=632.8nm，利用Matlab编写预定面形计算程序可以得到主镜的面形值。结合主动力解算模块可以求出促动器组的最大载荷为107N，超出促动器量程100N。主动力优化模块以促动器的最大载荷100N为优化目标，优化变量为像差的幅值，优化后得到像差幅值为0.467λ。优化后的主镜像散的面形值见表5，根据面形校正矩阵K和像散面形X可以计算得到面形校正所需主动力的值，见表6所示。

表5　像散面形值

表6　像散校正主动力值

从表6可以看出，促动器组的最大载荷为99.64N，小于促动器的最大调整力100N，主镜像散的最大校正能力为0.467个波长。

4　结论

本文主要是对某大型天文望远镜的主镜镜面主动光学进行研究。首先研究了主镜面形校正算法，设计了主镜及主动支撑模型，并利用Isight平台建立了主镜面形校正矩阵求解模型。然后研究了主镜慧差的校正精度。最后研究了主镜的低阶像散的校正能力。分析结果表明：主镜慧差的校正精度在4%以内；促动器调整力为100N时，能校正0.467个波长的低阶像散。主镜面形校正算法及模型准确，可以用来进行主镜面形校正。

［1］Douglas Neill，George Angeli，Chuck Claver.Overview of the LSST active optics system：Modeling，SystemsEngineering，andProjectManagementfor Astronomy VI［C］.Washington，USA：SPIE，2014.

［2］Lee Dettmann，Dave Ashby，John M.Hill.A laser tracker active optics system for the Large Binocular Telescope：Ground-based and Airborne Telescopes V［C］.Washington，USA：SPIE，2014.

［3］David S.Ashby，Christopher Biddick，John M.Hill. Active optics controldevelopmentattheLBT：Ground-basedandAirborneTelescopesV［C］. Washington，USA：SPIE，2014.

［4］AlessandroZuccaroMarchi，PascalHallibert，Joao Pereira do Carmo.Active optics for space applications：an ESA perspective：Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation［C］.Washington，USA：SPIE，2014.

［5］Daniele Gardiol，Gerardo Capobianco，Daniela Fantinel.Active optics system of the ASTRI SST-2M prototype for the Cherenkov Telescope Array：Advances in Optical and Mechanical Technologies for TelescopesandInstrumentation［C］.Washington，USA：SPIE，2014.

［6］Brian McLeod，Antonin H.Bouchez，Brady Espeland.TheGiantMagellanTelescopeactive optics system：Ground-based and Airborne Telescopes V［C］.Washington，USA：SPIE，2014.

［7］Douglas Miller，John M.Hill，Taras Golota.Active optics operations at the Large Binocular TelescopeGround-basedandAirborneTelescopesV［C］.Washington，USA：SPIE，2014.

［8］PietroSchipani，DemetrioMagrin，LotharNoethe. The active optics system of the VST：concepts and results：Ground-based and Airborne Telescopes IV［C］.Washington，USA：SPIE，2012.

［9］Ming Liang，Victor Krabbendam，Charles F.Claver. Active optics in Large Synoptic Survey Telescope：Ground-basedandAirborneTelescopesIV［C］. Washington，USA：SPIE，2012.

［10］Renaud Bastaits，Bilal Mokrani，Goncalo Rodrigues. Dynamics，active optics，and scale effects in future extremely large telescopes：Ground-based and Airborne Telescopes IV［C］.Washington，USA：SPIE，2012.

Research on the Large Space Telescope Primary Mirror Active Optical System Based on ISIGHT Platform

ZHANG Lihao，ZHANG Yuanqing，DONG Jihong，SUN Yang
（Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033）

In order to realize the high image quality of large telescopes，the primary mirror active optical system model is established.The primary mirror deformation correction algorithm，the precision of the deformation correction and the ability of deformation correction are studied.First，The primary mirror deformation correction algorithm is studied.The structure of the primary mirror and the support are designed，and the primary mirror finite element model is established.Primary power matrix constructed units force matrix and the primary mirror deformation matrix are constructed，

generalized inverse matrix method is used to obtain the primary mirror deformation correction matrix.Then the correction precision analysis model of primary mirror deformation is established by using Isight platform.The primary mirror deformation correction precision is analyzed by taking coma as an example.Finally，the correction ability analysis model of primary mirror deformation is established by using the Isight platform.The correction ability of the primary mirror deformation is analyzed by taking astigmatism as an example when the actuators max adjustment force are 100N.The analysis results show that coma correction precision is about 4%；Active actuator can correct 0.467 wavelength astigmatism.The primary mirror deformation correction algorithm and model are accuracy，and can be used for the primary mirror image correction.

primary mirror；active optics；Isight platform；deformation correction

TN205；TH161.1

A

1672-9870（2016）04-0020-05

2016-03-01

张立浩（1985-），男，博士，助理研究员，E-mail：4027356@qq.com