量子进化算法在极紫外多层膜表征和设计中的应用

梅雪峰，匡尚奇，谢耀

（1.长春理工大学理学院，长春　130022；2.中国科学院长春光学精密机械与物理研究所，长春　130033）

量子进化算法在极紫外多层膜表征和设计中的应用

梅雪峰1，匡尚奇1，谢耀2

（1.长春理工大学理学院，长春130022；2.中国科学院长春光学精密机械与物理研究所，长春130033）

针对EUV多层膜的表征和设计过程中普遍采用的遗传算法（GA）存在的大种群和求解效率低的问题，本文将实数编码量子进化算法（QEA）应用于EUV多层膜的表征和宽光谱EUV多层膜的设计过程中。分别采用实数编码GA和QEA对理论仿真的EUV多层膜的X射线掠入射反射谱进行反演拟合和宽光谱EUV多层膜的反射谱进行设计，进而将QEA在EUV多层膜表征和设计方面的性能进行对比分析。分析结果表明，QEA在多层膜的表征方面具有小种群和反演求解效率高的优点，多层膜的膜厚拟合精度可达±0.1nm；在多层膜设计方面，量子进化算法同样具有小种群的优势，同时求解效率较GA算法接近，设计的多层膜反射率带宽为13～15nm，反射率可达25%。相关工作展现出QEA算法在多层膜研发方面的应用价值，为进一步工作打下基础。

EUV多层膜；量子进化算法；膜系设计

在极紫外（EUV）波段，几乎所有物质的折射率均接近于1，且具有较强的吸收，所以不能采用传统的透过式光学系统，而采用基于EUV多层膜的反射式光学系统。为获得尽可能高的反射率，传统的EUV多层膜多采用等周期的膜系结构，如周期Mo/ Si多层膜在13.5nm附近可实现近70%的反射率。但是，在EUV光刻、EUV光学检测、EUV天文学等诸多领域中，最高的峰值反射率不是必需的，此时周期多层膜过窄的反射光谱带宽（一般为0.5nm）带来了一系列的弊端，比如造成宽带EUV光源的巨大能力损失。为解决此问题，非周期EUV多层膜的研发得到了国内外关注，成为研究热点。对此，德国IOF研究所研制出正入射反射率近20%、带宽为2.33nm的EUV多层膜［1-3］；美国Lawrence国家实验室研制出45˚角入射反射率近20%、带宽为3nm的EUV多层膜［4］；国内同济大学的科研小组研制出正入射反射率近10%、带宽近16nm的EUV多层膜［5，6］。上述宽光谱EUV反射镜的多层膜均采用了非周期膜系设计，以低反射率为代价实现较宽的光谱带宽，虽然在相应的研制方面取得了一定的进展，但由于非周期多层膜的设计所要优化的膜层参数较多，一般难度较大。

在EUV波段，多层膜各膜层较薄（＜10nm），膜层间的扩散对光谱性能有很大影响，精确表征难度较大［7］，所以其理论模拟与膜系设计难度较高，进而限制了EUV多层膜的发展。在EUV多层膜的实验表征方面，普遍采用的方法有掠入射X射线反射（GIXR）和透射电子显微镜（TEM）。TEM虽然可直接对EUV多层膜的微观结构进行观测，但却是一种破坏性检测方法，并且检测精度不高，一般作为多层膜表征的参考［7，8］。与之相比，GIXR是一种无损检测方法，检测精度较高，但却是一种间接表征方法，需建立相应的理论模型，并且对拟合求解的算法要求较高［9-11］。在EUV多层膜表征的理论模型方面，科研人员对周期多层膜的二层模型进行了修正，唯象地提出了四层模型［8-10］。四层模型是在Mo和Si膜层构成的二层模型的基础上，考虑膜层间的扩散层，并认为扩散层由Mo和Si发生化学反应生成的化合物（如MoSi2）构成。虽然四层模型更接近EUV多层膜的实际微观结构，并且理论模拟结果与实验结果更一致，但该模型却使需求解的多层膜参数数量成倍增长，对GIXR的拟合算法提出了更高的要求。

在上述EUV多层膜的表征和设计领域，传统采用的优化算法为遗传算法（GA）［9，10］，但传统的遗传算法存在着种群规模大、寻优过程复杂和求解效率低的问题。量子进化算法（QEA）是一种将量子计算与进传算法相结合的优化算法，其以量子计算的一些基本概念和理论为基础，用量子位编码表示染色体，通过量子门的旋转完成优化搜索，具有种群规模小、收敛速度快、全局寻优能力强的特点［12］，在处理某些优化问题，如0-1背包问题［13］、旅行商问题［14］和数值优化问题［15］已取得了较好的结果。目前，QEA在国内外的工程技术领域均得到了广泛的应用，取得了令人满意的结果［16-18］。针对传统遗传算法在EUV多层膜表征和设计领域的问题，本文采用实数编码QEA［15］应用于其相关研究中，并将其优化效率与基于实数GA的求解效率进行比较分析。

1　Mo/Si多层膜的反射理论

EUV多层膜的膜层之间存在扩散，而扩散层厚度与粗糙度直接影响了多层膜的光学性能，而EUV多层膜多采用Mo和Si交替的膜层结构。因此，为了表征多层膜的扩散信息，本文采用基于图1所示的4层模型对具有m个周期的Mo/Si多层膜的反射谱进行理论模拟（扩散层为MoSi2）。

图1　四层模型的Mo/Si多层膜的结构示意图

Mo/Si多层膜反射率的计算采用菲涅尔公式的循环递推法。以S偏振光为例，第j层的反射率振幅Rj为

其中

而

在（1）-（3）式中，nj、θj、σj和tj分别为第j层膜的折射率、入射角、粗糙度和厚度，而λ为入射光波长。一般假设基底为半无限大介质，所以R0=0。通过对反射率振幅进行迭代计算，就可以计算出最上层的反射率，即多层膜的反射率为Rcalc.=|Rn|2。需要说明的是复折射率n=（1-δ）-iβ，其中

式（4）中的re、N、M、ρ分别为电子经典半径、阿佛加德罗常数、材料相对原子质量和材料密度，而Xi为相应原子的原子比例，和是原子散射因子（数据来源于Lawrence Berkeley National Laboratory数据库）。上述计算方法不仅适用于计算Mo/Si多层膜的GIXR（λ=0.154nm），同样适用于计算多层膜的EUV反射谱（λ=12～14nm）。

2　基于QEA的EUV多层膜的表征

2.1理论模拟的EUV多层膜GIXR

多层膜表征算法的首要问题是验证算法的自洽性，即反演求解的多层膜结构应该与设计的结构参数相符。所以，首先应提高GIXR理论模拟的仿真程度，尽可能使理论模拟结果接近真实实验结果，然后以理论仿真结果作为反演求解的目标，进而验证反演结果与设计参数之间的误差和算法的可行性。Mo/Si多层膜的GIXR的基本理论与1节中的内容相同，其光源为波长为0.154nm左右的硬X射线，以往的相关研究中对X射线衍射仪的角分辨率进行了分析，图2中给出了相应的等周期Mo/Si多层膜的GIXR的理论模拟，相应的Mo/Si多层膜结构参数见表1。但是，上述理论模拟的GIXR与实验检测结果还是存在一定的差别，一方面表现为模拟反射峰均是对称的，而实验中的反射峰，特别是大角度的反射峰存在一定的不对称性；另一方面实验结果具有较大的随机背景噪声。针对上述问题，本文对GIXR实验中的X射线光源的双光谱线和反射的背景噪声进行了进一步的理论模拟，以提高多层膜GIXR的仿真程度。首先，针对X射线光源的CuKα-1（0.15405nm）和CuKα-2（0.15443nm）的双光谱线，分别计算其相应的GIXR，并按照双光谱线的光强比（2∶1）进行加权平均，进而得到考虑光源双光谱线的GIXR模拟结果，如图2中的划线所示。图2中的结果表明，在仅考虑光源的CuKα-1的单一光谱线的情况下，Mo/Si多层膜的GIXR的反射峰是对称的，而在考虑光源的双光谱线的情况下，多层膜的GIXR反射峰出现了不对称现象，进一步提高了理论模拟的仿真度。其次，针对GIXR实验结果中的背景噪声，本文采用正态分布的随机数进行模拟，其表达式为其中I为反射强度，IR为未考虑背景强度下的反射强度，Ib为固定的GIXR的背景强度。G（0， Δ2）为均值为0的高斯分布随机数，其方差为Δ，考虑背景噪声的GIXR的模拟结果如图2中的点线所示。

图2　未考虑X射线光源双线光谱线和背景噪声的Mo/Si多层膜的GIXR（实线）；仅考虑X射线光源双线光谱线的Mo/Si多层膜的GIXR（划线）；X射线光源的双光谱线和背景噪声都予以考虑的Mo/Si多层膜的GIXR（点线）。

图2中的结果表明，与实验强度相当的随机背景噪声（固定背景强度为Ib=3×10-8，随机噪声为高斯分布，方差为Δ=0.6）对大角度的X射线反射峰造成很大的影响，甚至可将其完全淹没，进而无法识别。对Mo/Si多层膜的GIXR进行检测和分析，可以获得较高精度的多层膜的微观结构信息，但其缺点是测量信号随机噪声较高。在考虑X射线衍射仪光源的双光谱特性和背景噪声的随机波动后，理论模拟的多层膜的GIXR的仿真程度进一步提高，为接下来的基于实数编码QEA的反演求解提供了拟合目标。

2.2基于QEA对理论模拟的多层膜GIXR的反演求解及其与基于GA的结果的比较

本节以实数编码QEA［15］为基础，建立适用于Mo/Si多层膜GIXR的反演求解程序。首先，对多层膜的结构参数进行量子编码，建立种群规模N= 10的量子种群Q，量子种群Q表示为

其中第i个个体的染色体为

式中tSi和tMo分别为Si层和Mo层的膜层厚度，tMS和tSM分别为MoSi2（Mo on Si）层和MoSi2（Si on Mo）层的膜层厚度；dSi、dMo和dMS分别为Si、Mo和MoSi2的膜密度，σ为膜层的粗糙度。染色体量子基因的实数分量对应Mo/Si多层膜的微观结构参数，而染色体的量子位由概率幅［cosθj，isinθj，i］T构成。基于QEA建立等周期Mo/Si多层膜的GIXR的反演拟合程序流程如图3所示。

图3　基于QEA建立的周期Mo/Si多层膜的GIXR的反演流程图

在图3所示的流程中，参数初始化设置QEA的种群规模为N=10，初始旋转角θ0=0.01π。在互补变异阶段，连续“求精”搜索次数为m1=5，连续“求泛”搜索次数为m2=5。在离散交叉过程中，选择优秀个体数s=2，每个优秀个体连续交叉次数为m3=8。在个体评价过程中，针对周期Mo/Si多层膜GIXR的拟合评价函数为：

其中χ2为评价系数，n为拟合选取的点数，Rc（）i为第i个点的理论计算值，而Rm（）i为第i个点的实验测量值或理论仿真模拟值。

图4　基于QEA和GA针对理论模拟的Mo/Si多层膜的GIXR的反演求解的评价系数与进化代数的关系

为检验基于QEA的等周期Mo/Si多层膜的GIXR的反演方法的求解效率，以2.1节中理论模拟的GIXR（图2中的点线）为反演目标，采用最大进化代数100代为终止条件进行反演求解，进化过程中最优个体的的评价系数χ2如图4所示。同时，为了更好地对QEA的求解效率和精度进行分析，以相同的理论模拟的GIXR为反演目标，采用GA进行求解，并对两种算法的结果进行对比分析。对于基于GA的反演程序，相关参数为种群规模N=100，交叉概率pc=0.9，交叉算子ηc=1，变异概率pm=0.15，变异算子ηm=1和进化终止条件为进化100代。基于GA的反演求解中最佳个体的评价系数χ2同样列于图4中（点划线）。对图4进行分析表明，虽然QEA所采用的种群规模（N=10）远小于GA的种群规模（N=100），但在整个进化过程中，QEA的反演求解质量大都优于GA，且其收敛速度和求解效率均优于GA。这一结果证明，QEA具有较强的并行运算功能和全局搜索能力，不仅适用于简单函数的求解［15］，而且在实际技术领域同样具有潜在的应用价值。同时，基于QEA的反演拟合程序在进化的初始阶段就可以得到较高质量的解，这证明基于QEA的Mo/Si多层膜结构参数的反演求解的方法是完全自洽的。

表1　基于QEA和GA，以理论仿真的Mo/Si多层膜的GIXR为反演目标，经过100代进化后获得的多层膜的最优结构参数，以及各参数的搜索区间和Mo/Si多层膜的理论设计值

表1给出了基于QEA和GA建立的多层膜GIXR的反演求解进化100代后得到的最佳参数解，将优化参数对比分析表明，在各参数搜索范围相同的情况下，QEA相比GA可在小种群的条件下，获得更高精度的膜层厚度（拟合精度优于±0.1nm）以及扩散层MoSi2的物理特性参数。需要指出的是，对于基于四层模型的Mo/Si多层膜，扩散层MoSi2的参数对多层膜的表征和设计起到了非常重要的作用，因此，基于QEA的反演算法较基于GA的算法可获得较高精度的多层膜微观结构表征。此外，由于作为拟合求解目标的多层膜GIXR考虑了随机噪声，所以基于QEA建立的反演算法具有一定的抗干扰能力。

为进一步表征基于QEA和GA反演求解的Mo/ Si多层膜结构参数的准确性，图5给出了基于表1中的结构参数理论模拟的多层膜的GIXR，并将相应结果与2.1节中理论模拟的仿真结果进行对比。对比结果表明，基于QEA反演求解的多层膜结构参数精度较高，计算的曲线与理论仿真的曲线符合的很好。

图5　基于QEA和GA反演优化的最优多层膜参数计算的GIXR，以及反演求解的拟合目标

3　基于QEA的宽光谱EUV多层膜的设计

3.1宽光谱EUV多层膜的设计方法

在宽光谱EUV多层膜的设计方面，设计模型同样有二层模型和四层模型两种理论模型，四层模型的膜系设计结果与基于二层模型的膜系设计结果相比与实验结果符合的更好，所以本文采用四层模型对宽光谱EUV多层膜进行设计，由于四层模型中，膜层的厚度，特别是MoSi2扩散层较薄，所以可以近似认为其物理性质不变，而采用表1中的相关参数，仅对四层模型中的Mo和Si的膜层的厚度进行搜索优化。基于QEA，首先对非周期Mo/Si多层膜的Mo和Si膜层厚度进行量子编码，建立种群规模N=10的量子种群P。量子种群P表示为

其中任意第i个个体的染色体为

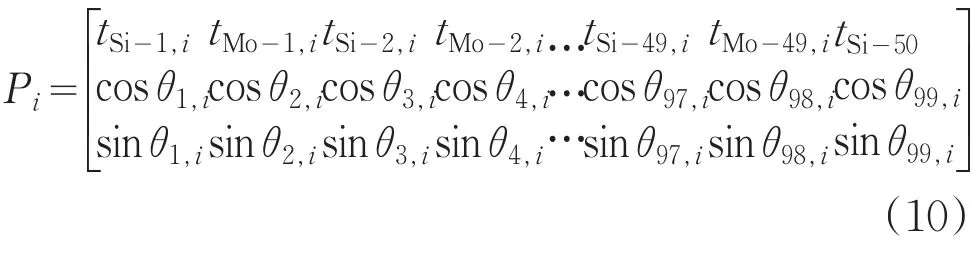
其中tSi和tMo分别为Si层和Mo层的膜层厚度。染色体量子基因的实数分量对应搜索优化的Mo层和Si层的厚度，而染色体的量子位相应的概率幅为［cosθj，isinθj，i］T。其次，采用与图3相同的流程进行优化搜索，其中参数初始化过程中，初始旋转角θ0=0.01π。在互补变异阶段，连续“求精”搜索次数m1=5，连续“求泛”搜索次数m2=5。在离散交叉过程中，选择优秀个体数s=2，每个优秀个体连续交叉次数m3=8。在种群个体的评价过程中，对非周期Mo/Si多层膜的评价函数为

其中MF为个体的评价系数，λ1和λ2为设计的宽反射谱的波长的上下线，Rm为设计的反射光谱曲线（对于宽光谱的设计反射率为Rm（λ）=0.25（13.0nm≤λ≤15.0nm）），而Rc为依据某一个体计算的非周期Mo/Si多层膜的反射光谱曲线。最后，QEA的终止条件为进化2000代。

3.2基于QEA的宽光谱EUV多层膜的设计和基于GA的设计结果的比较

在基于QEA的宽光谱多层膜的设计中，每代最优个体的评价系数MF随着代数的演进如图6所示，从图中可以看到，虽然QEA算法的种群较小（N= 10），但是膜系的优化效果较好，在进化1000代后，已经进化出可接受的膜系结构。为了更好地评估QEA在多层膜设计方面的效率，采用同样的进化目标和进化终止条件，采用实数编码GA进行搜索寻优，并对基于两种算法的进化过程和寻优结果进行对比分析。在基于GA的进化中，种群规模N= 100，交叉概率和交叉算子分比为pc=0.9和ηc=1，变异概率和变异算子分别为pm=0.15和ηm=1，而基于GA的宽光谱多层膜设计中，每代最优个体的评价MF也列于图6中。对图6中基于两种算法的结果对比表明，在进化的初始阶段，基于GA的寻优的膜系优于基于QEA的寻优的膜系质量，但随着进化的进一步进行，在进化约1000代后，基于QEA的寻优结果逐渐接近基于GA的寻优结果。需要指出的是，QEA所采用的种群规模N=10，其规模不仅远小于GA算法的种群规模N=100，而且远小于膜系设计所要寻优的参数个数（Mo和Si膜层厚度总计99的参数），而这是GA算法采用同样种群规模所不可能做到的，所以QEA可以以较小的计算复杂度实现与GA相接近的寻优效果，进而体现出QEA较强的并行运算功能和全局搜索能力。

图6　基于QEA和GA的宽光谱EUV多层膜的评价系数MF与进化代数之间的关系

图7　基于QEA和GA的优化的最优膜系计算的多层膜反射谱和标准周期多层膜的反射谱

为验证基于QEA和GA的宽光谱非周期Mo/Si多层膜膜系设计的正确性，分别计算两种算法进化2000代后的最优解的膜系的反射光谱，相应的结果见于图7之中。从图7中可以发现，基于GA和QEA的膜系优化方法均给出了比较理想的宽带EUV反射光谱，在波长13.0～15.0nm的光谱范围内，反射率可达（25±2）%，且反射带的半峰宽度（FWHM）达2.33nm。基于QEA和GA设计出的非周期多层膜较传统的周期多层膜带宽（图7中黑色点线）均有较大的提高，进而验证了QEA在EUV多层膜设计领域的可行性。

图8　基于QEA和GA算法优化出的Mo/Si多层膜的膜系

图8给出了QEA和GA进化2000代后，优化得到的最优膜系的膜层结构，其中（a1）和（b1）分别为基于QEA优化得到的Si层和Mo层的膜层厚度；（a2）和（b2）分别为基于GA优化得到的Si和Mo的膜层厚度。比较表明，两种寻优算法得到的膜系结构有很大的区别，其原因在于QEA较传统的GA的寻优路径有较大的不同，这也为镀膜工艺提供了另一种可供选择的膜系结构。

4　结论

针对传统遗传算法在EUV多层膜表征和设计中存在的种群大和求解效率低的问题，本文将实数编码的QEA应用于EUV多层膜的表征和宽光谱EUV多层膜的设计过程中，并将结果与基于实数编码的GA的结果进行对比分析。在EUV多层膜的表征方面，QEA具有小种群和求解效率高的优点，多层膜的膜厚拟合精度可达±0.1nm；在多层膜设计方面，QEA同样具有小种群的优势，同时求解效率较GA算法接近，而设计的多层膜反射率带宽为13～15nm，反射率可达25%。上述工作展现出QEA算法在EUV多层膜研发方面的潜在应用价值，一方面，除了本文涉及的宽光谱多层膜，还有窄带光谱多层膜、宽角度多层膜、偏振多层膜等更加复杂膜系的相关设计研究工作可采用QEA进行相关的尝试；另一方面，QEA是一个新兴的研究领域，其发展正处于一个快速和完善的过程中，其本身就有很多的工作需进一步深入研究，相关工作可提供适用于EUV多层膜研发的更加高效算法。

［1］Feigl T，Yulin S，Benoit N，et al.EUV multilayer optics［J］.Microelectronic Engineering，2006，83：703.

［2］Kuhlmann T，Yulin S，Feigl T，et al.Design and fabrication of broadband EUV multilayer mirror［J］. Proceedings of SPIE，2002，4688：509.

［3］Yulin S，Kuhlmann T，Feigl T，et al.Spectral reflectance tuning of EUV mirrors for metrology application［J］.Proceedings of SPIE，2003，5037：286.

［4］Aquila A，Salmassi F，Dollar F.Development in realistic design for aperiodic Mo/Si multilayer mirrors［J］.Optics Express，2006，14：10073.

［5］Wang Z，Michette A.Optimization of depth-graded multilayer coating for broadband reflectivity in the soft X-ray and EUV region［J］.Optics Communication，2000，177：47.

［6］Tan M，Li H，Huang Q，et al.Mo/Si aperiodic multilayer broadband reflective mirror for 12.5～28.5nm wavelength range［J］.Chin.Opt.Lett.，2011，9：23-102.

［7］Aschentrup A，Hachmann W，Westerwalbesloh T，et al.Determination of layer-thickness fluctuations in Mo/Simultilayersbycross-sectionalHR-TEM and X-ray diffraction［J］.Applied Physics A，2003，77：607.

［8］Yulin S，Feigl T，Kuhlmann T，et al.Interlayer transitionzonesinMo/Sisuperlattices［J］.J.Appl. Phys，2002，92：1216.

［9］A.D.Dane，A.Veldhuis，L.M.C.Buydens，et al Application of genetic algorithms for characterization ofthinlayeredmaterialsbyglancingincidence X-ray reflectometery［J］.Physica B，1998，253：254.

［10］M.Sánchez del Río，G.Parechi，Global optimization and reflectivity data fitting for X-ray multilayer mirrors by means of genetic algorithms［J］.Proceeding of SPIE，2001，4145：88.

［11］A.E.Yakshin，E.Louis，P.C.Görts，et al，Determination of the layered structure in Mo/Si multilayers by grazing incidence X-ray reflectometry［J］. Physica B，2000，283：143.

［12］G.X.Zhang.Quantum-inspired evolutionary algorithms：a survey and empirical study［J］.J.Heuristics，2011，17：303.

［13］K.H.Han，J.H.Kim.Quantum-inspired evolutionary algorithm for a class of combinatorial optimization［J］.IEEETransactionsonevolutionary computation，2002，6：580.

［14］A.Narayanan，M.Moore.Quantum-inspired genetic algorithms［C］.Proceedings of IEEE International Conference on Evolutionary Computation，Nagoya，Japan：1996.

［15］高辉，张锐.改进实数编码量子进化算法及其在参数评估中的应用［J］.控制与决策，2011，26：418。

［16］J.G.Vlachogiannis，K.Y.Lee.Quantum-inspired evolutionary algorithm for real and reactive power dispatch［J］.IEEE transactions on power systems，2008，23：1627.

［17］罗洪明，王家映，朱培民，等.量子遗传算法在大地电磁反演中的应用［J］.地球物理学报，2009，52：260.

［18］邹益民，汪渤.基于量子遗传算法的滤波器参数优化［J］.系统工程与电子技术，2009，31：1346.

Application of the Quantum Evolutionary Algorithm in Researches of EUV Multilayer

MEI Xuefeng1，KUANG Shangqi1，XIE Yao2

（1.School of Science，Changchun University of Science and Technology，Changchun 130022；
2.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun，130033）

According to the shortcomings in the characterization and design of EUV multilayer with the genetic algorithm（GA），which are large population，slow convergence and poor accuracy，the application of real-code quantum evolutionary algorithm（QEA）in the characterization and design of EUV is demonstrated.The fitting of grazing incidence X-ray reflection（GIXR）of EUV multilayer and design of broadband EUV multilayer have been carried out based on the real-code QEA，and the results are compared with that obtained based on real-code GA.The results demonstrate that the real-code QEA which has a smaller population can supply the parameters of multilayer with better convergence and accuracy in the fitting of GIXR，and the deviation of thickness of multilayer can be lower than 0.1nm. Comparing with GA，the real-code QEA which use a smaller population can also supply a good coating design with a similar convergence and accuracy，and the reflection band of designed multilayer is 13～15nm，which has a reflectivity of 25%.As a result，the related researches demonstrated the potential value of practical application of real-code QEA in the characterization and design of EUV multilayer，and the foundation has been laid for the researches in the next-step.

EUV multilayer；quantum evolutionary algorithm；coating design

O484

A

1672-9870（2016）04-0001-07

2016-04-25

国家自然科学基金青年基金项目（61405189）；吉林省自然基金项目（20150101019JC）

梅雪峰（1991-），男，硕士研究生，E-mail：275986817@qq.com

匡尚奇（1981-），男，副研究员，E-mail：physicskuang@163.com