基于相似度及直觉模糊熵的多属性群决策方法

韩二东 郭 鹏 赵 静

(西北工业大学 管理学院, 陕西 西安 710072)

基于相似度及直觉模糊熵的多属性群决策方法

韩二东 郭 鹏 赵 静

(西北工业大学 管理学院, 陕西 西安 710072)

针对决策者权重与属性权重完全未知的直觉模糊多属性群决策问题，提出一种基于相似性测度及直觉模糊熵的群决策方法。基于相似性测度计算两两决策者之间关于各方案在单个属性下的相似度，得到决策个体与决策群体之间关于单个属性的平均相似度，求得各决策者在各方案下关于单个属性的决策者权重。按属性对直觉模糊评估信息求直觉模糊熵得到各属性权重，由IFWA算子计算各方案的综合直觉模糊评价值，通过得分函数得到各方案的优劣次序。投资公司的项目选择算例说明了该方法的有效性和可行性。

多属性群决策；直接模糊数；相似度 ；直觉模糊熵

Atanassov[1]于1986年提出了直觉模糊集的概念。Chen[2]采用记分函数解决Vague集模糊多属性决策问题，Bustince[3]等指出Vague集实质上是直觉模糊集，更加突显出直觉模糊集在处理模糊评价信息方面的优势。

为对直觉模糊评价信息进行有效集结，在定义直觉模糊数基本运算的基础上，徐泽水等[4]提出了一系列的直觉模糊信息集成算子，陈华友[5]、He Y D[6]考虑到不同直觉模糊数的隶属度与非隶属度之间可能存在的交叉影响，改进了直觉模糊基本运算并提出了新的信息集成算子，新算子稳健性较好，能够避免得出与实际相悖的决策结果，对隶属度或非隶属度为零的特例有着较好的可解释性。

如何确定直觉模糊多属性决策问题的各决策者权重及属性权重是此类决策问题的关键。最近，采用距离测度及相似性测度解决直觉模糊多属性决策问题的方法逐渐增多，但已有的距离测度或相似度测度方法所得结果多为实数形式，会造成评估信息的丢失。基于此，Wang[7]等定义了新的直觉模糊相似度，将直觉模糊决策矩阵转化为相似矩阵，计算结果为直觉模糊数，很好的保留了各属性评价信息，但新的定义不完全满足相似度的性质，且对各属性同等对待，对属性权重的认定较为粗糙。

一、多属性群决策方法及步骤

此相似度定义满足直觉模糊相似度定义的4个性质条件。由直觉模糊数之间的相似度公式可计算任意两决策者在方案下关于属性评价值的相似度，即

针对各方案的单个属性相似度转换值，关于不同的决策者进行归一化处理，得到各方案下每个属性所体现出的决策者权重，即

各属性所确定的权重为:

由各属性权重及IFWA算子得到各方案的综合评价值，即

根据各方案综合评价值的得分函数对其排序，最终得到各方案的优劣次序。

基于以上分析，决策者权重及属性权重完全未知的直觉模糊多属性群决策方法步骤如下：

步骤1: 由式(2)计算两两决策者之间关于各方案在单个属性评价值下的相似度，将相似度矩阵转化为精确数矩阵，并由式(3)计算每个决策者与决策群体关于单个属性的平均相似度，得到各决策者的平均相似度矩阵；

步骤2:根据式(4)对方案 下关于属性 的平均相似度进行归一化处理，接着采用式(5)得到对各直觉模糊决策矩阵加权，得到群体直觉模糊决策矩阵；

步骤3:根据式(6)求各属性的直觉模糊熵，并基于式(7)得到各方案关于单个属性的平均直觉模糊熵，通过式(8)得到各属性权重；

步骤4 :采用式(2)，式(9)计算各方案的综合评价值，通过得分函数实现对综合评价值的排序，得到各方案的排序结果。

二、算例分析

某投资公司有3个可投资的项目，分别是汽车营销公司、食品加工公司、计算机研制公司，拟通过面临的风险情况预期盈利情况社会政策影响情况环境影响情况、公司发展前景这5个属性对3个投资项目进行评估，共聘请了3位不同领域的专家，各专家针对3个投资方案的5个不同的属性，给出如下直觉模糊数的评估矩阵：

可计算两两决策者之间关于各方案在单个属性评价值下的相似度构成的相似度矩阵，并取风险因子为0，即以最保守的方式将相似度矩阵转化为精确数矩阵其中

接着得到各决策者的平均相似度矩阵分别为：

基于归一化处理后的各方案关于每个属性的决策者权重，加权得到群体直觉模糊决策矩阵为：

由群体直觉模糊矩阵及直觉模糊熵公式，得到如下直觉模糊熵矩阵：

从而得到各属性权重为：

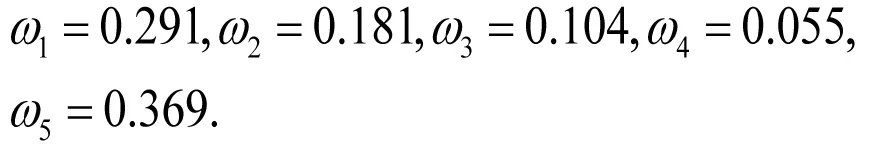
基于IFWA算子及各属性权重，得到各方案的综合评价值分别为：

由直觉模糊数排序的得分函数，可得3个方案的优劣次序为，即应当选择汽车公司作为拟投资的对象。

三、结 语

针对现有基于相似度确定属性权重的不足，本文提出一种新的直觉模糊相似度度量方法，并基于两两决策者之间关于每个方案在各属性下的平均相似度得到决策者权重，对集结所得群体直觉模糊决策矩阵，由直觉模糊熵确定各属性权重，并由IFWA算子得到各方案的综合评价值，通过综合评价值的得分函数得到各方案的优先序。给出的相似度度量方法所得结果仍为直觉模糊数，尽量避免评价信息的损失。单个属性下各个方案评价值的直觉模糊熵越大，则该属性下评价信息的有效性越差，对方案排序所起的作用越小，基于此确定各属性权重。投资项目选择算例体现出该群决策方法的有效性和合理性，今后可继续探讨直觉模糊决策问题中的决策者权重及属性权重确定方法，为直觉模糊决策提供更多途径。

[1]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[2]Chen S M, Tan J M.Handling Multi-criteria Fuzzy Decision Making Problems Based on Vague SetTheory[J].Fuzzy Sets and Systems, 1994, 67(2): 163-172.

[3]Bustince H, Burillo P.Vague Sets Are Intuitionistic Fuzzy sets[J].Fuzzy Sets and Systems, 1996, 79(3): 403-405.

[4]Xu Z S.Intuitionistic Fuzzy Aggregation Operators[J].IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1179-1187.

[5]陈华友, 何迎东, 周礼刚等.广义直觉模糊加权交叉影响平均算子及其在多属性决策中的应用[J].控制与决策, 2014 (7).

[6]He, Y D, Chen H Y, Zhou L G, et al.Intuitionistic Fuzzy Geometric inTeraction Averaging Operators andTheir Application to Multi-criteria Decision Making[J].Information Sciences, 2014, 259(2): 142-159.

[7]Wang Z, Xu Z S, Liu S S, et al.A Netting Clustering Analysis Method under Intuitionistic Fuzzy Environment[J].Applied SoTh Computing, 2011, 11(8):5558-5564.

[8]Xu Z S.Some Similarity Measures of Intuitionistic Fuzzy sets and Their Applications to Multiple Attribute Decision Making[J].Fuzzy Optimization Decision Making, 2007, 6(2): 109-121.

C934

A

1003-1154(2016)01-0105-03

10.3969/j.issn.1003-1154.2016.01.034

国家自然科学基金项目(71272049)；高等学校博士学科点专项科研基金项目(20126102110052).