基于TVP-VAR模型的利率变动与股市波动的时变关系研究

胡一博

（西北工业大学 自动化学院，陕西 西安710072）

基于TVP-VAR模型的利率变动与股市波动的时变关系研究

胡一博

（西北工业大学 自动化学院，陕西 西安710072）

采用时变参数向量自回归模型，实证研究了利率、股价与股市波动率三者之间的动态时变联动关系。研究结果表明：利率变动对股票市场在不同时期的影响不同；利率变动对股票市场的短期结构冲击显著；同时研究还发现我国股市具有较强的投机性。

利率；股市；TVP-VAR模型

在实际经济运行过程中，利率变动对股票市场具有直接、迅速的影响。分析利率变动与股市波动之间的时变关系，有利于把握货币市场与股票市场间的动态联动关系，为货币当局更好的利用利率政策调控股市提出更具价值的政策建议。传统的现值模型把利率与股价的关系描述为P=D/R, 其中P为股票价格、D为股息收入、R为利率。传统经济理论认为股票价格与利率成反比。然而近些年，越来越多的经济学家和学者运用向量自回归（VAR）等计量模型对这一问题进行研究。Bernanke[1]等运用VAR模型通过对美国股市的研究发现，当联邦基金利率每下调0.25%，就会引起股票价格1%的增加。而Alatiqi[2]等运用VAR模型对美国利率变动与股市波动的相关关系进行分析，得出利率变动对股市波动影响不显著的结论。Basisth[3]和Mayes[4]等学者的研究则发现，利率政策对股票价格的影响并不确定，利率与股价的相关关系与经济周期的变动有关。

纵观在这一研究领域已有的文献，大多数都采用传统计量模型进行实证研究，且结论并不一致。而较多的研究方法，如向量自回归，都是假设模型参数不随时间变化。但由于研究时间跨度较大，随着时间的推移，经济周期、政策偏好和其他经济变量等因素不断发生变化，模型参数不可能保持不变。所以本文使用带有时变参数的向量自回归模型（TVP-VAR）对这一问题进行分析，是本文的创新点所在。

一、数据说明与理论模型

（一）数据的选取及处理

由于我国在2005年4月进行了股权分置改革，股市监管更加严格，也更加市场化。为避免以往数据的干扰，本文选取了从2005年4月到2015年8月的利率、股价和股市波动率的月度数据作为样本进行研究，共125组数据。

本文选用银行间7天同业拆借利率作为利率政策的代理指标，并取月对数增长率。在反映股市波动方面本文选取两个指标：在反映股票价格变化方面，本文选取沪深300价格指数，并取月对数收益率,即It=lnIt-lnIt-1；在反映股市波动率方面选取的指标是日收益率的标准差，并用移动平均法计算月度数据，所有数据均来自WIND数据库。本文采用ADF单位根检验，对所有数据的平稳性进行分析。结果表明，三个变量都是平稳的时间序列，均不存在单位根，满足构建TVP-VAR模型的要求。

（二）理论模型

Nakajima为了允许截距项、方差以及VAR系数都可以随时间变化，对向量自回归模型提出了一套新的算法，形成了TVP-VAR模型。该算法把一个标准的VAR模型进行了如下变化，首先定义一个标准的VAR模型为：

其中B为p×p维联立系数矩阵，yt为p×1维观测向量，E1…Es是p×p维滞后系数矩阵，模型中扰动项μt为p×1维结构性冲击。假定结构冲击间的关系服从递归识别，即矩阵B为下三角阵，模型（1）可整理为：

其中Xt是通过单位矩阵和变量向量滞后期向量的克罗内克乘积所构建的矩阵，βt、Bt、∑t表示三个具有时变性的状态方程，分别为自回归系数矩阵、同期关系系数矩阵和方差-协方差矩阵。设bt=(b21，b31，b41，…，bp，p-1) ′为 Bt下三角矩阵的堆栈，设ht为矩阵∑t的下三角部分向量。参数服从随机游走过程，该模型的动态变化是由以下公式决定：βt+1=βt+μβt，bt+1=bt+μbt，ht+1=h1+μht，并且存在如下关系：

本文采用20000次MCMC抽样实现对参数βt、Bt、∑t的估计1，并基于125组样本抽样做出下文中的统计推断。

二、实证分析结果

（一）TVP-VAR模型的参数估计结果

表1中参数检验的Geweke值均未超过5%的临界值1.96，这表明Geweke统计量在95%的置信度水平下，不能拒绝参数收敛于后验分布的原假设。无效因子值表示为得到不相关样本所需要抽样的次数，也就是说，无效因子的数值越小表示样本越有效。表1中参数的无效因子值均小于90，表明本文所使用的125组数据的预测模拟可以使MCMC模拟收敛。

表1 TVP-VAR模型的参数估计结果及诊断

（二）时变参数的特征分析

在参数不变模型向量自回归模型中，模型估计后参数都只有一个估计值。但在TVP-VAR模型中，每个参数的估计值都是随时间变化的。图1展现了模型中 Sβ1，Sβ2，Sb1，Sb2，Sh1，Sh2这 6 个参数的样本抽样模拟路径。参数的模拟路径体现出明显的波动聚类现象，并且在模拟尾部各参数均收敛于样本均值的估计结果。

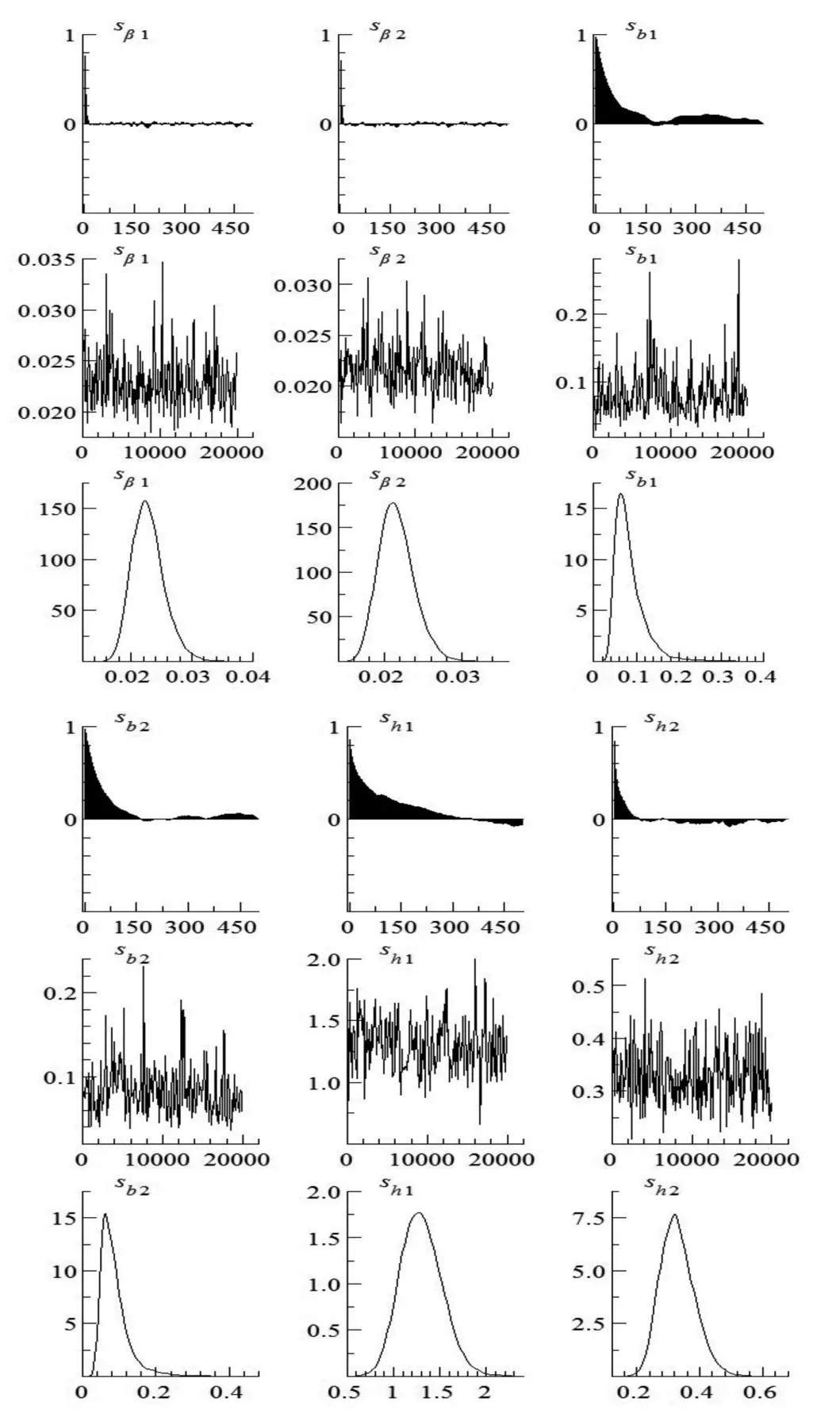
图1 时变参数的特征

图2 变量同期关系的时变特征

图3 不同时滞期的脉冲响应图

（三）利率、股价、股市波动率相互影响关系的时变特征分析

图2描述了利率，股价，股市波动率之间的动态联动时变关系。由图2中的第1个子图可见，利率在不同时期对股价的影响是截然不同的。在2009年之前，利率对股价的影响系数ã（r→i）为正，2009年至2013年之间利率对股价的影响系数接近0值，而2013年以后利率与股价呈负相关关系，且在2015年前后影响系数接近-0.5。由此看来利率对股价的影响在近10年内经历了一个正相关→不相关→负相关的周期。结合2013至2015年利率下调后股市的表现，本文发现利率与股票价格有显著的负相关关系，这表明利率政策对股票市场的传导渠道正逐步畅通。第2个子图反映了利率对股市波动率的时变影响ã（r→f），这一图形与子图1相似，这一表现也与客观经济规律相符。第3个子图反映了股价对股市波动率的影响，影响系数ã（i→f）在近10年来均大于2，由此可见股价变动对股市波动率有较大的影响，并且这种影响关系在2009年后保持持续上升的态势。

（四）利率、股价、股市波动率在不同时滞期的脉冲响应分析

对于TVP-VAR 模型，可以设置不同的滞后期数，这样在针对各变量间的脉冲响应进行分析时，可以清晰的反映单位冲击变量对被冲击变量在不同滞后期形成的影响。为了描述不同时期利率对股市的影响情况，本分分别选取1个月（短期冲击）、3个月（中期冲击）和6个月（长期冲击）的标准正向冲击形成三种时期的脉冲响应时间序列图。图3的三个子图中，实线分别代表了利率对股价（εr→i）、利率对股市波动率（εr→f）、股价对成股市波动率（εi→f）在不同时期的短期结构冲击关系。而虚线部分别代表的是三者中期和长期的结构冲击关系。通过比较可以发现，利率对股价和股市波动率的短期结构冲击显著，而中长期结构冲击相对不显著；而股价对股市波动率的结构冲击同样为短期显著。

三、结 论

本文构建了一个含有利率、股价和股市波动率的TVP-VAR模型，分析了三者之间的动态时变联动关系，可以看出时变模型可以更好的解释利率变动与股市波动的相关关系，也与实际情况相符。通过上文分析可以发现，近10年我国利率变动与股市波动经历了正相关、不相关和负相关的一个周期，这也体现出了货币政策的利率政策传导渠道在逐步畅通。利率调控手段相对传统的靠货币供应调控，具有迅速、直接等特点，但同时也应注意在运用利率政策调控时需充分考虑其对股市造成的影响。

通过上文对不同时期的脉冲响应冲击分析可以看出，利率对股市的冲击主要表现为短期效应，利率对股市的中长期影响不显著。同时，研究还发现股价对股市波动率的影响系数较大，而且保持持续上升趋势。股市波动率过高是股市不成熟、不稳定的表现，也是造成股灾的主要原因。在中国股票市场上，投资者们盈利的主要方式就是价低时买入、价高时卖出，从中赚取利益，投资者很少关注于时间价值投资，股价上涨靠题材，而利率作为股市的“风向标”恰恰在这时发挥了关键作用。然而利率下调后股价迅速的上涨和股市过高的波动率，容易产生集群效应，从而引发股灾，并对实体经济产生不利影响。综上所述，我国政府在运用利率政策调控时需充分考虑其对股市造成的影响，引导股市健康的发展。

[1]Ben S Bernanke,Kenneth N Kuttner.What Explains the Stock Market’s Reaction to Federal Reserve Policy[J].The Journal of Finance, 2005 ,60(3): 1221-1257.

[2]Alatiqi.The Impact of Monetary Policy Shocks on Stock Prices[J].Journal of International Money and Finance,2008,29(5):879-896.

[3]Basistha A ,Kurov.Macroecnonmic Cycles and the Stock Markets Reaction to Moneraty Policy[J].Journal of Banking and Finace,2008,32 (12):2606-2616.

[4]Mayes.Dynamic Linkages between Monetary Policy and the Stock Market[J].Economic Inquiry,2012, 73(3):171-193.

F224.12

A

1003-1154(2016)01-0007-03

10.3969/j.issn.1003-1154.2016.01.003

国家社科基金青年项目（15CJY034）.

1 具体算法参见Nakajima(2011) TVP-VAR手册