基于基线漂移校正的旅行时间预测模型*

朱广宇　杜崇　张彭

(1. 北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044; 2.北京城市交通协同创新中心,北京 100022; 3.上海交通大学,系统控制与信息处理教育部重点实验室, 上海 200240; 4.北京市交通发展研究中心城市交通运行仿真与决策支持北京市重点实验室, 北京 100073)



基于基线漂移校正的旅行时间预测模型*

朱广宇1,2,3杜崇1,2张彭4

(1. 北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044; 2.北京城市交通协同创新中心,北京 100022; 3.上海交通大学,系统控制与信息处理教育部重点实验室, 上海 200240; 4.北京市交通发展研究中心城市交通运行仿真与决策支持北京市重点实验室, 北京 100073)

路段旅行时间及其预测值是管理部门实施交通流组织,提供交通信息服务的重要依据,也是出行者合理选择出行路径的重要参考.文中基于浮动车检测数据研究了路段旅行时间的计算算法及数据预处理方法;分析了旅行时间序列中的基线漂移现象,并运用小波分析法给出了基线漂移的校正方法以达到对时间序列降噪处理的目的;最后,基于自回归移动平均法建立了路段旅行时间的预测模型，并选取实际数据验证了文中模型的有效性和精确性.

浮动车;旅行时间预测;基线漂移;小波分析;自回归移动平均法

路段旅行时间及其预测是管理部门实施交通流组织、提供交通信息服务管理的重要前提依据和基本保障,也是出行者合理选择出行路径的重要参考[1- 2],因此国内外学者对旅行时间的预测高度重视,并且研究出了多种预测方法,如基于时间序列的方法、轨迹法、指数平滑预测、Kalman滤波等[3- 6].Silvia等[7]以意大利某城市为例,基于阶段预测模型建立了旅行时间的预测模型;Haworth等[8]基于本地在线的岭回归分析法对旅行时间进行预测;Hofleitner等[9]使用交通流模型和机器学习理论建立了基于数据挖掘思想的预测模型.

近年来,随着浮动车检测技术的逐步成熟,学者们开始基于浮动车检测数据研究旅行时间的获取和预测模型,如Jones等[10]利用相邻线路的浮动车检测数据,使用地理空间推理方法建立了路段旅行时间的预测模型;Li等[11]基于浮动车数据,利用速度定位法对路段旅行时间进行预测;Tulic等[12]利用日常和季节性案例建模计算期望旅行时间,通过估计旅行时间的期望偏差来提高预测的精确性;Li等[13]利用K-均值聚类,决策树及神经网络方法,建立了基于数据挖掘的旅行时间预测模型.

部分学者发现,一类路段旅行时间序列中带有基线漂移现象,即在旅行时间的数据获取过程中,由于数据采集设备及数据传输装置中存在干扰,使得时间序列数据的基线呈现上下漂移的现象,这种现象会改变旅行时间序列图形的形状,从而影响最终数据的分析评价效果.时间序列中的基线漂移现象会影响预测精度,因此,可以采用滤波的方式对基线漂移噪声进行处理,以降低其对信号质量的影响.如孙明丽[14]通过自适应滤波处理心电信号中的基线漂移噪声;Mecozzi[15]基于多项式曲线拟合法对环境学样本中氢氧化物色谱中的基线漂移进行处理；Zhang[16]基于ARMA和卡尔曼模型,校正气体传感器时间序列数据中的基线漂移;Ara等[17]则基于小波变换法对ECG信号中的基线漂移噪声进行处理.

通过上述分析可知,发现并对旅行时间序列中的基线漂移现象进行分析和处理是提高旅行时间序列预测结果精度的重要途径.由此,文中首先基于浮动车检测数据对路段旅行时间进行计算和预处理,然后对旅行时间序列中的基线漂移现象进行分析,并采用小波分析给出了时间序列中基线漂移的校正方法，最后基于自回归移动平均法建立了路段旅行时间的预测模型.

1　路段旅行时间计算方法及数据的预处理

1.1基于浮动车检测数据的路段旅行时间计算

路段旅行时间通常由速度计算获得,而浮动车检测直接提供的速度值是车辆的瞬时速度,瞬时速度随机性大,不能精确反映浮动车在路段中的行驶速度,故文中引入计算速度[18]的概念计算路段旅行时间：

(1)

(2)

1.2旅行时间数据预处理

图1为连续4日基于浮动车检测数据计算获取的旅行时间数据.由于环境干扰及采集系统精度问题会导致旅行时间数据的波动,影响预测精度,因此需要对旅行时间序列数据进行预处理.

图1　连续4日24 h数据分布中的异常数据

Fig.1Abnormal data in the data distribution of 24 hours in a duration of 4 days

首先,定义缺失时间为5 min以上的数据为丢失数据,不进入历史标准库计算;其次,需要判断数据的有效性.表1所示为某大城市中不同等级道路的有效性样本量标准,当实时数据样本量不能保证有效性标准时,则利用历史上同一路段同一时刻的数据代替这一时刻的数据.

表1　不同等级道路的有效样本量标准

最后,根据交通参数的合理范围定义错误数据.以速度数据为例:

0≤speed≤fv·speed限速

(3)

式中:speed为浮动车原始速度,fv为修正系数,一般取1.3;speed限速为道路的限制速度,不同等级道路的限制速度不同.

2　小波去噪及自回归移动平均模型

2.1小波去噪原理

小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求.

旅行时间序列中的噪声可以分为两类,一类是由于随机干扰导致的白噪声,另一类则是时间序列中发生基线漂移而产生的基线噪声.为了提高预测精度,需要对基线漂移进行校正.由于小波分析方法既可以校正基线漂移,又能去除时间序列中的白噪声,故文中选取小波分析方法作为旅行时间数据的降噪处理方法.

2.1.1小波去噪

小波变换[19]具有时-频局部化特征,在低频段采用高的频率分辨率和低的时间分辨率,在高频段采用低的频率分辨率和高的时间分辨率,非常适合于分析有突变的信号.

设Ψ(t)是平方可积函数,即Ψ(t)∈L2(R),若Ψ(t)的傅里叶变换Ψ(ω)满足条件:

(4)

则称Ψ(t)为一个基本小波或小波母函数,称式(4)为小波函数的可容许性条件.

将小波母函数Ψ(t)进行伸缩和平移得小波基函数:

(5)

式中，a为伸缩因子(又称尺度因子),b为平移因子.

WTf(a,b)=〈f(t),Ψa,b(t)〉=

(6)

Donoho提出的硬阈值函数为

(7)

软阈值函数为

(8)

2.1.2基线漂移校正

利用小波变换提升算法进行基线漂移校正的步骤如下:

步骤2交替地进行预测和更新步骤.将滤波器P对偶信号作用以后作为奇信号的预测值.这里进行4步提升及对偶提升得到

步骤4第二代小波的重构过程基本是分解的逆过程.先进行尺度变换,然后进行更新和预测步骤,最后进行奇偶分解的逆变换,可以重构恢复信号.

2.2自回归移动平均模型(ARMA)

自回归移动平均方法由自回归模型(AR模型)与滑动平均模型(MA模型)混合构成[22].

(1)自回归过程(AR)

令Yt表示t时期的旅行时间.Yt的模型可以描述为

(Yt-δ)=α1(Yt-1-δ)+ut

(9)

式中,δ为Y的均值,ut为具有零均值和恒定方差σ2的不相关随机误差项(即ut是白噪音),称Yt遵循一阶自回归或AR(1)随机过程.

p阶自回归函数形式为

(Yt-δ)=α1(Yt-1-δ)+α2(Yt-2-δ)+

α3(Yt-3-δ)+…+αp(Yt-p-δ)+ut

(10)

(2)移动平均过程(MA)

利用MA模型同样可以产生Y.Y的模型也可以描述为

Yt=μ+β0ut+β1ut-1

(11)

式中,μ为常数,u为白噪音(零均值,恒定方差,非自相关)的随机误差项.t时期的Y等于一个常数加上现在和过去误差项的一个移动平均值,则称Y遵循一阶移动平均或MA(1)过程.

q阶移动平均可以写成

Yt=μ+β0ut+β1μt-1+β2μt-2+…+βqμt-q

(12)

(3)若Y兼有AR和MA的特性,则为ARMA过程.Y可以写成

Yt=θ+α1Yt-1+β0ut+β1ut-1

(13)

式中,若有p个自回归项和q个移动平均项,则记为ARMA(p,q),θ为常数项.

3　旅行时间预测实例分析

文中选用某大城市北三环马甸桥至安华桥路段的旅行时间序列作为原始数据(如图2所示),数据的采集周期为1.5min.

3.1旅行时间序列的小波降噪处理

利用式(1)、(2)对浮动车检测数据进行转换计算,获取旅行时间数据,并采用2.2节中的方法对数据进行预处理,得到旅行时间序列,如图3所示.利用小波变换对旅行时间序列进行降噪处理,时序中的基线漂移如图4所示.图5为利用小波变换去除时间序列中的高频噪声和基线漂移误差后得到的时间序列图.图6为小波分析降噪前后时间序列对比图.

图2　数据采集路段位置示意图

图3　预处理后的旅行时间序列

图4　基线漂移图

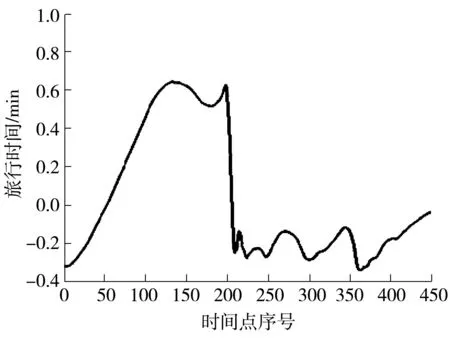
图5　去除基线漂移噪声的时序图

图6　降噪前后旅行时间序列对比图

Fig.6Comparison before and after noise reduction of the travel time series

3.2面向拟合度的ARMA模型参数调节及预测模型选择

选取小波分析降噪后的旅行时间序列作为预测的输入数据,使用负二项分布概率变点模型对旅行时间序列状态变点的存在位置进行搜索[23],搜索结果表明时间序列图形位于统计时间点序号[1,265]区间的部分包含时间序列曲线中75%的状态变点,故将旅行时间序列数据以第265个数据点为界划分为拟合区和验证区,如图7所示.

图7　模型拟合区及模型验证区划分图

Fig.7Division of model fitting area and model validation area

利用拟合区数据对ARMA模型的参数进行计算.首先从AR模型开始,为保证结果的完整性和精确性,应遍历所有p,q值,故从(p,q)的初始值(1,1)开始选取.当p取1时,拟合度为50.99%,得到如下结果：其拟合数据曲线趋势与验证数据曲线趋势大体相同,但两条曲线间存在较大的相位差,这说明此参数组合拟合度较低.

连续提高AR模型阶数,计算可知二阶AR模型的拟合度达到了72.26%,如图9所示,相对于一阶AR模型图8有大幅度提高.

而三阶AR模型所得的拟合度为73.16%,如图10所示,相对于二阶AR模型拟合度并没有大幅度提高,故不再使用AR模型,转而使用ARMA模型拟合,几组参数的拟合结果如图11所示.

图8　一阶AR模型拟合结果

图9　二阶AR模型拟合结果

图10　三阶AR模型拟合结果

图11　ARMA模型拟合结果

图11中am×pq∶α表示：当ARMA的参数p、q取特定值时拟合度为α.从图11可知,当ARMA的参数p取2、q取3时,拟合度最高,达到74.06%,加入AR模型的拟合结果,如图12所示.

当ARMA模型的参数取p=2、q=3,p=3、q=4以及p=3、q=3时,拟合度较高,为最适合的拟合模型.

利用能谱置信区间、自相关残差图、99%置信水平区间分布3种指标对以上3种参数条件下的ARMA进行检验,结果分别如图13-15所示.

图12　全部拟合结果

图13　能谱置信区间

图14　自相关残差图

图15　99%置信水平区间分布

由能谱分析可知,3种拟合模型在低频处的置信度均较低,高频处置信度均较高,故无法作为模型选取依据.根据自相关残差图,ARMA(3,3)以及ARMA(3,4)模型的自相关残差大多落在在99%置信范围之内,说明在对拟合结果的自相关控制检验过程中未出现异常,数据偏移量均处于统计控制状态之内,结果可信.由图15可知ARMA(3,4)模型的99%置信水平区间分布较广,因此选取ARMA(3,4)模型作为最终选定的拟合模型.

3.3预测结果及误差分析

使用最终选取的ARMA(3,4)模型对路段旅行时间进行预测,得到最终预测结果如图16所示.

图16　预测值与拟合值对比图

文中采用平均绝对误差、均方误差、均方根误差、标准误差、平均绝对百分比误差5个误差指标对预测结果进行分析.5个误差指标的计算公式分别如下.

平均绝对误差:

(14)

(i=1,2,…,n)

均方误差:

(15)

(i=1,2,…,n)

均方根误差:

(16)

(i=1,2,…,n)

标准误差:

(17)

(i=1,2,…,n)

(18)

(i=1,2,…,n)

经过计算得到误差指标值:MAE=0.105,MSE=0.033,RMSE=0.041,S=0.019,MAPE=0.33%.由误差结果可知,预测值误差较小,ARMA(3,4)模型对旅行时间的预测效果非常理想.经过小波分析校正基线漂移后,通过自回归移动平均方法建立的旅行时间预测模型确实提高了旅行时间预测的精度.

4　结论

首先提出了旅行时间序列中的基线漂移现象.然后利用小波分析的方法予以校正,以此对时序进行降噪.最后利用自回归移动平均方法构建了旅行时间预测模型.最终得到的预测数据误差较小,表明对基线漂移进行校正后,能提高模型的预测精度.

[1]YANX,ZHANGH,WUC.Researchanddevelopmentofintelligenttransportationsystems[C]∥DistributedComputingandApplicationstoBusiness,Engineering&Science(DCABES).[S.l.]:IEEE,2012:321- 327.

[2]CHOWDHURY Nk,LEUNG Cks.Improved travel time prediction algorithms for intelligent transportation systems[M].Berlin:Spring Berlin Heidelberg,2011:355- 365.

[3]LI Zhi-peng,HONG Y,LIU Yun-cai,et al.An improved adaptive exponential smoothing model for short-term tra-vel time forecasting of urban arterial street [J].Acta Automatica Sinica,2008,34(11):1404- 1409.

[4]沈旅欧,庄岩浩,刘伟铭等.基于修正算法的高速公路路段旅行时间估计 [J].华南理工大学学报(自然科学版),2015,43(4):20- 27.

SHEN Lü-ou,ZHUANG Yan-hao,LIU Wei-ming,et al.Estimation of expressway section travel time based on correction a lgorithm [J].Journal of South China University of Technology(Natural Science Edition),2015,43(4):20- 27.

[5]WU C H,HO J M,LEE D T.Travel-time prediction with support vector regression [J].IEEE Transactions on Intelligent Transportation Systems,2004,5(4):276- 281.

[6]赵建东,王浩,刘文辉，等.高速公路旅行时间的自适应插值卡尔曼滤波预测 [J].华南理工大学学报(自然科学版),2014,42(2):109- 115.

ZHAO Jian-dong,WANG Hao,LIU Wen-hui,et al.Prediction of expressway travel time based on adaptive interpolation kalman filtering [J].Journal of South China University of Technology(Natural Science Edition),2014,42(2):109- 115.

[7]SILVIA Barbetta,TOMMASO Moramarco,LUCA Brocca,et al.Confidence interval of real-time forecast stages provided by the STAFOM-RCM model:the case study of the Tiber River(Italy) [J].Hydrol Process,2014,28(3):729- 743.

[8]HAWORTH James,SHAWE-TAYLOR John,CHENG Tao,et al.Local online kernel ridge regression for forecasting of urban travel times [J].Transportation Research(Part C),2014,46:151- 178.

[9]HOFLEITNER Aude,RYAN Herring,BAYEN Alexandre,et al.Arterial travel time forecast with streaming data:a hybrid approach of flow modeling and machine learning [J].Transportation Research,Part B,Methodological,2012,46B(9):1097- 1122.

[10]JONES M,GENG Y,NIKOVSKI D,et al.Predicting link travel times from floating car data [C]∥Intelligent transportation systems-(ITSC),16th International.[S.l]:IEEE,2013:1756- 1763.

[11]LI Yu-guang,SHI Chao-yang,LI Qing-quan.Link travel time estimation based on large-scale low-frequency floating car data [C]∥2013 the International Conference on Remote Sensing,Environment and Transportation Engineering(RSETE 2013).[S.l.]:Atlantis Press,2013.

[12]TULIC M,BAUER D,SCHERRER W.Link and route travel time prediction including the corresponding reliability in an urban network based on taxi floating car data [J].Transportation Research Record:Journal of the Transportation Research Board,2014(2442):140- 149.

[13]LI C-S,CHEN M-C.A data mining based approach for travel time prediction in freeway with non-recurrent congestion [J].Neuro Computing,2014,133:74- 83.

[14]胡迎接.基于曲线拟合和滤波的FTIR-ATR基线漂移处理算法研究 [D].合肥:安徽大学电气工程与自动化学院,2014.

[15]MECOZZI M.A polynomial curve fitting method for baseline drift correction in the chromatographic analysis of hydrocarbons in environmental samples [J].APCBEE Procedia,2014,10:2- 6.

[16]ZHANG L.Time series estimation of gas sensor baseline drift using ARMA and Kalman based models [J].Sensor Review,2015,36(1):34- 39.

[17]ARA I,HOSSAIN M,MAHBUB S.Baseline drift removal and de-noising of the ECG signal using wavelet transform [J].International Journal of Computer Applications,2014,95:15- 17.

[18]朱爱华.基于浮动车数据的路段旅行时间预测研究 [D].北京:北京交通大学交通运输学院,2007.

[19]王芳.小波分析在信号去噪中的应用研究 [D].成都:西华大学电气与电子信息学院,2009.

[20]韦力强.基于小波变换的信号去噪研究 [D].长沙:湖南大学电气与信息工程学院,2007.

[21]DONOHO D L.De-noising by soft-thresholding [J].IEEE Transactions on Information Theory,1995,41(3):613- 627.

[22]ROJAS I,VALENZUELA O,ROJAS F,et al.Soft-computing techniques and ARMA model for time series prediction [J].Neuro Computing,2008,71(4):519- 537.

[23]夏媛媛,马立云,王晓原等.交通流在间歇流状态下的概率变点模型 [J].山东理工大学学报(自然科学版),2011,25(4):12- 16.

XIA Yuan-yuan,MA Li-yun,WANG Xiao-yuan,et al.A probability change-point model for traffic flow in the intermittent condition [J].Journal of Shandong University of Technology(Science and Technology),2011,25(4):12- 16.

s: Supported by the General Program of National Natural Science Foundation of China(61572069,61503022) and the National Key Technology Research and Development Program of the Ministry of Science and Technology of China(2014BAG01B02)

A Travel Time Forecasting Model Based on Baseline Drift Correction

ZHUGuang-Yu1,2,3DUChong1,2ZHANGPeng4

(1.Key Laboratory of Urban Transportation Complex Systems Theory and Technology of the Ministry of Education, Beijing Jiaotong University, Beijing 100044, China;2.Center of Cooperative Innovation for Beijing Metropolitan Transportation, Beijing 100022, China; 3. Key Laboratory of System Control and Information Processing of the Ministry of Education, Shanghai Jiaotong University, Shanghai 200240, China;4.Beijing Municipality Key Laboratory of Urban Traffic Operation Simulation and Decision Support, Beijing Transportation Research Center, Beijing 100073, China)

Road travel time and its forecasting value are the important bases of urban traffic management and traffic information service, and they are also an important reference for travelers to choose their reasonable traveling routes. In this paper, first, a calculation algorithm and a preprocessing method of urban travel time data are presented. Then, the status of the baseline drift in road travel time series is analyzed, and a method to correct the baseline drift is put forward by utilizing the wavelet analysis method, so as to reduce the noise of travel time series. Finally, a road travel time forecasting model is constructed based on the auto-regressive and moving average (ARMA) model, and it is proved to be valid and accurate by using actual data.

floating car; travel time forecasting; baseline drift; wavelet analysis; auto-regressive and moving average model

2015- 11- 30

国家自然科学基金面上项目(61572069,61503022);国家科技支撑计划项目(2014BAG01B02);北京交通大学中央高校基本科研业务费专项资金资助项目(2014JBM211)；河北省交通运输厅科技项目(A0201-150505)；交通部青年科技英才培养项目(201540)；城市交通运行仿真与决策支持北京市重点实验室资助项目(BZ0012)

朱广宇(1972-),男,副教授,主要从事智能交通系统、交通系统工程研究.E-mail:gyzhu@bjtu.edu.cn

1000- 565X(2016)08- 0131- 08

U 491

10.3969/j.issn.1000-565X.2016.08.019