心电信号中基线漂移的去除方法比较及算法实现

【作 者】陈苹，叶继伦, ，张旭, ，陈刚

1 深圳大学医学院生物医学工程系，深圳市，518060 2 广东省生物医学信号检测与超声成像重点实验室，深圳市，518060 3 深圳市生物医学重点实验室，深圳市，518060

0 引言

心电信号是生物医学信号中一种低幅低频的微弱信号。基线漂移一般是由于人体呼吸、电极运动等引起，其一般小于1 Hz[1]。常用的去除方法有中值滤波法[2]、小波变换法[3]、形态学滤波法[4]等。本文简单介绍了几种常用方法并用Matlab实现。以下用于处理的原始心电信号是截取自MIT-BIH数据库的序号为103和114两种数据中的一段数据，我们通过对比基线漂移严重和微弱两种情况，比较各种方法的优劣之处，其中103为较严重漂移的心电数据，114为漂移较为微弱的心电数据。

1 方法

1.1 中值滤波法

中值滤波的定义[5]就是取信号中的某一点前的N（N为奇数）个数据，将这N个数据进行排序，取数据的中值，将数据的中值作为该点的数据。将整段信号都做以上处理，提取出漂移信号，将原始信号减去漂移信号，便得到滤波后的效果。测试效果如图1、图2所示。

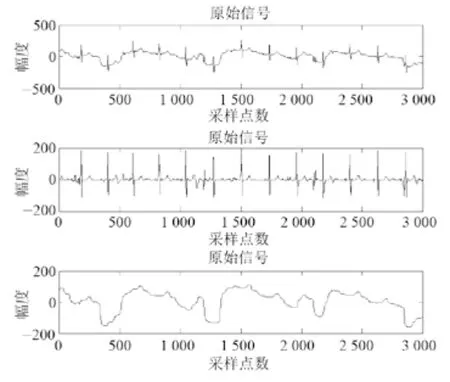
图1 中值滤波去除严重基线漂移Fig.1 Median filtering removes severe baseline drift

1.2 高通滤波法

基线漂移的频率成分较低，所以用高通的方法对基线漂移的去除也有一定的效果。IIR滤波器能用较低的阶数获得较高的频率选择性，但不具有线性相位[6]。由于心电信号的处理对线性相位的要求不是很高，所以可以选择IIR滤波器。这里我们选用butterworth滤波器，截止频率为1 Hz。测试效果如图3、图4所示。

图2 中值滤波去除微弱基线漂移Fig.2 Median filtering removes weak baseline drift

图3 高通滤波去除严重基线漂移Fig.3 High-pass filtering removes severe baseline drift

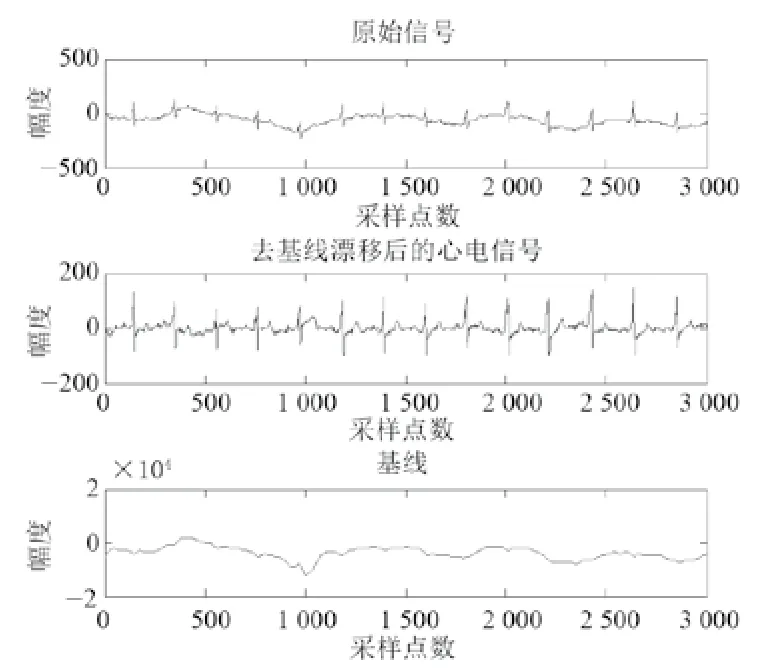
图4 高通滤波去除微弱基线漂移Fig.4 High-pass filtering removes weak baseline drift

1.3 小波变换法

根据小波变换多分辨分析理论，对含噪信号进行多尺度小波分解后，可以利用信号和噪声在频谱和能量分布上的不同，直接将噪声所对应的小波分解尺度上的细节分量去除，然后利用小波逆变换进行信号重构，就可以有效去除信号中的噪声成份。经过试验得到，采用小波函数db8对原始信号进行8个尺度的分解，第8层分解的信号频率与基线漂移的频率接近，因此将前7层信号重构，去除第8层信号，即可得到去除基线漂移的信号。测试效果如图5、图6所示。

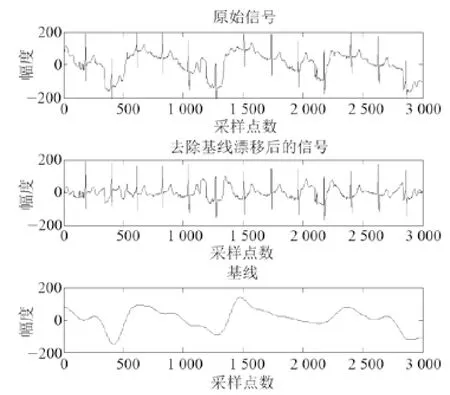
图5 小波变换去除严重基线漂移Fig.5 Wavelet transform to remove severe baseline drift

图6 小波变换去除微弱基线漂移Fig.6 Wavelet transform to remove weak baseline drift

1.4 曲线拟合法

曲线拟合法去基线漂移是利用多项式拟合估计基线漂移，再从原始信号中减去此基线漂移。曲线拟合就是通过需要处理的数据，利用数据来求取近似函数。曲线拟合并不要求函数的曲线通过所有离散点，只要求近似函数能够反映这些离散点的一般趋势，不出现局部波动。曲线拟合的常用方法一般是基于最小二乘法，在以下处理中，我们选用最小二乘法进行拟合。测试效果如图7、图8所示。

图7 曲线拟合去除严重基线漂移Fig.7 Curve fitting removes severe baseline drift

图8 曲线拟合去除微弱基线漂移Fig.8 Curve fitting removes weak baseline drift

1.5 基于心电信号特征点的方法

此方法是找出波形上的所有的R波的峰值点，通过三次样条插值拟合出基线，将原始信号减去基线就可去除基线漂移。寻找R波的算法是基于Pan&Tompkins算法，通过三次样条插值拟合出这些点连成的基线，此方法去基线漂移后的效果如图9、图10所示。

1.6 形态学滤波法

数学形态学（Mathematical Morphology）的基础是不同的集合运算，主要包括膨胀、腐蚀、开运算、闭运算等[4]。下面介绍形态学滤波的原理。

设信号序列为f(n)(n=0, 1,......N-1)，结构元序列为g(m)(m=0, 1,......M-1)，其中N＞M。

图9 特征点滤波去除严重基线漂移Fig.9 Feature point removes severe baseline drift

图10 特征点滤波去除微弱基线漂移Fig.10 Feature point removes weak baseline drift

1）膨胀运算：

其中n=M-1, M,... , N-1。

2）腐蚀运算：

其中n=0, 1,..., N-M。

3）开运算：

图11是形态学滤波去除基线漂移的流程图，图12、图13是信号经过形态学滤波后对比图。

2 总结与讨论

本文选用两种数据段，序号103中截取的数据段是漂移比较严重的情况，序号114中截取的数据段是漂移较为微弱的情况，我们通过以上方法对两种情况进行数据分析和对比，进行总结。

图11 形态学滤波去除基线漂移的流程图Fig.11 Flow chart of morphological filter to remove the baseline drift

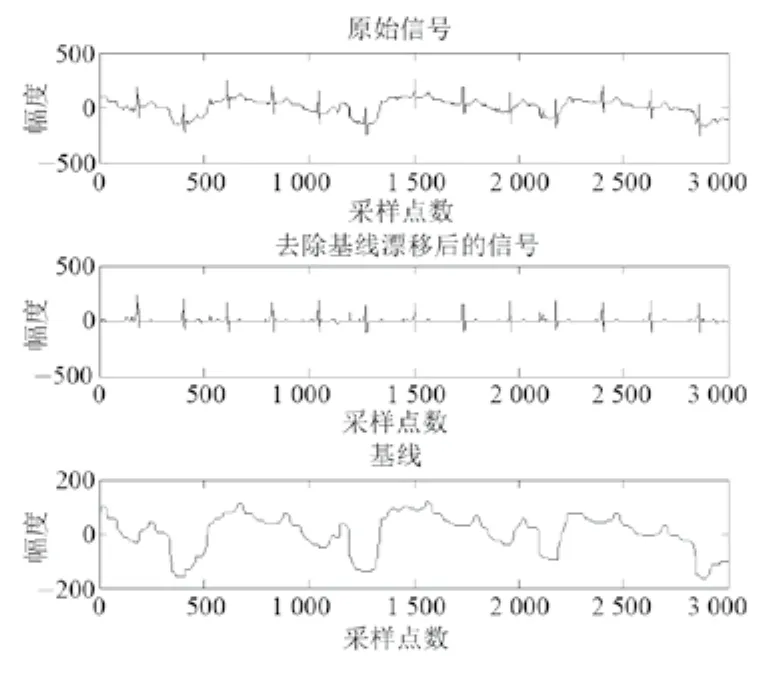
图12 形态学滤波去除严重基线漂移Fig.12 Morphological filter remove severe baseline

图13 形态学滤波去除微弱基线漂移Fig.13 Morphological filter remove weak baseline drift

中值滤波是一种非线性平滑技术，在心电信号中对于严重和微弱的基线漂移抑制效果明显，而且对ST段也有保护作用，但是对高斯噪声影响很大的情况下，效果比较差。

高通滤波的方法虽然能对严重基线漂移有一定的效果，但是对ST段的影响较大，幅形失真较大。在基线漂移比较微弱的情况下，高通滤波能达到一定的去除效果。

小波变换抑制基线漂移，是根据频域上的相似来达到抑制基线漂移的目的，选择尺度合适的情况下，滤波的效果较好，但是运算量比较大，而且由于噪声频带往往与有用信号的频带有部分重叠，部分有用信息可能会丢失。

曲线拟合法最主要的有两点直线拟合，抛物线拟合及三次样条函数拟合等。直线拟合适用于基线漂移不太严重的时候，其优点是算法简单，速度快，但当基线漂移严重的时候，误差较大。用三次样条函数估计基线，效果较好。但是此方法与处理信号的长度有关，难以满足实时性要求。

基于心电信号特征点的算法，应用较好，我们需要在提取心电波形特征点如P起点和峰值点的基础上达到抑制基线漂移的目的，但是使用时的算法复杂，且滤波后的波形在一定程度上产生了严重失真。

形态学滤波算法简单，实时性好，抑制效果明显，两种情况下的抑制漂移效果都较为明显。其中结构元长度的选取是关键，选取不合适的情况下会导致波形损失。

因此，通过以上方法的算法比较，各种方法都有优缺点，可通过实际情况和场合选择适合的滤波方法对心电信号中的基线漂移进行去除。例如，在基线漂移不严重的情况下，我们可以选择曲线拟合法和高通滤波法、小波变换等，在漂移严重的情况下，我们可选择中值滤波和形态学滤波等方法，在漂移严重程度判别以及滤波方法及参数设置的智能选择上需要进一步根据应用要求进行匹配。