公路三维线形设计及约束建模

葛婷　符锌砂　李海峰　龙立敦　杨永红

(1.华南理工大学 土木与交通学院, 广东 广州 510640；2.苏州科技大学 土木工程学院,江苏 苏州 215011;3. 中南大学 地球科学与信息物理学院,湖南 长沙 410007)



公路三维线形设计及约束建模

葛婷1,2符锌砂1†李海峰3龙立敦1杨永红1

(1.华南理工大学 土木与交通学院, 广东 广州 510640；2.苏州科技大学 土木工程学院,江苏 苏州 215011;3. 中南大学 地球科学与信息物理学院,湖南 长沙 410007)

公路线形设计作为公路建设的重要环节，其设计质量的好坏直接影响到行车安全和舒适.为了改善现行平、纵分离式路线设计方法存在的不足，文中从公路中心线是一条空间曲线的本质出发，采用曲率和挠率作为设计参数，建立了一种新的公路三维线形设计方法.在此基础上，分别从几何连续性、车辆稳定性和行车舒适性3个方面对公路三维线形应满足的工程约束条件进行了研究分析，并建立了相应的约束模型.在借鉴现有设计规范和经验的基础上，结合已建立的约束模型，最终确定了不同设计速度下三维线形指标应满足的设计约束值.新的线形设计方法可以避免传统方法中平、纵线形组合无法量化分析，以及组合线形空间连续性衰减等问题，为提高公路线形设计的安全性提供了新的思路.

道路工程；三维线形设计；曲率；挠率；几何连续性；车辆稳定性；行车舒适性

公路线形设计作为公路建设的重要环节，其设计合理与否不仅直接关系到公路建设项目的质量好坏、投资成本，更直接影响到公路运行安全和行车舒适性[1].受现有计算机技术的限制和公路线形三维解析模型复杂性的影响，现行的公路几何设计通常将公路中心线拆分为平面和纵断面，然后通过平、纵组合形成空间曲线[2].这种人为拆分和组合式的设计方法在一定程度上增加了设计人员的操作量；同时，分离式的设计方法使得不同线形单元衔接和平、纵线形组合间的关系模糊不清，难以用统一的解析模型描述，线形设计的最终质量主要取决于设计人员的经验，给公路交通安全运营带来明显的弊端[3- 5].

为了改善线形设计对行车安全的影响，提高设计效率和设计质量，学者们开始研究公路三维线形设计[6- 8].Makanae[9]提出用以距离为参数的分段曲率和坡度函数进行公路三维几何线形设计的系统框架，其本质上仍是传统二维平、纵线形要素的组合叠加；林声等[10]采用空间曲率结合运行速度方面的特征修正，建立了以高速公路空间曲率为主要指标的道路安全评价模型，对现有设计线形进行安全性检查；Kuhn等[11]提出将路线设计、规范性检查和安全评价融合，建立集成的安全道路三维设计架构，通过可视化技术展现道路三维效果以进行实时动态设计.由于三维线形模型计算的复杂性，公路三维线形设计方法的研究尚处于起步阶段，相关研究文献和成果较少.目前已有的关于公路三维路线设计方面的研究多从静态角度出发，研究的焦点多集中在三维几何线形数学表达式的构建和描述上，相应的三维线形设计要素的选择和设计指标的控制多建立在传统二维平面设计的基础上，并未形成相对较为完善的体系.

忽视公路线形三维的本质特性而采用平、纵分离式设计方法是目前公路线形设计面临的主要困境之一，在设计中提高设计线形的安全性更是提高和改善目前公路安全运营水平的一项必不可少的措施.为此，文中从动态的角度出发，将公路线形看成是汽车行驶的轨迹，采用基本几何不变量弧长为参数，曲率、挠率为新的设计指标，提出了一种新的公路线形几何设计方法，并结合实际工程需求和现有路线设计经验，建立了相应的约束模型.

1　三维线形指标

公路中心线在三维空间上可看成是曲线上一点P从起点Ps移动到终点Pe的运动轨迹，在笛卡尔直角坐标系O-XYZ中，可用矢量形式表示，即：r=xi+yj+zk，其中i、j、k分别是沿X、Y、Z轴的单位向量(见图1).转换成参数方程形式表示，即

(1)

式中：x、y、z为坐标系O-XYZ上的投影大小，u为曲线参数，ub,ue分别为曲线起、终点坐标对应的参数取值.

图1　公路线形和Frenet标架说明

Fig.1Illustration of highway alignment and Frenet Frame

公路线形设计的一个基本原则是曲线应具有几何不变性，即设计曲线的形状不会随坐标系的改变而改变[12].故文中采用自然参数——弧长s作为曲线设计参数.对于空间曲线r(s)，其上任意一点均可确定一个由单位切矢T、单位主法矢N和单位副法矢B构成的坐标系，当参数s连续变化时，该坐标系也会随之连续发生平移和旋转，这样的坐标系称为弗朗内特(Frenet)活动标架[13]，见图1.该标架中的3个坐标轴还形成了3个坐标平面，分别为密切面(T-N平面)、法面(N-B平面)和从切面(T-B平面).相应的计算如下式所示：

(2)

当曲线上的点沿曲线移动时，该局部坐标系也会随之发生变化，这种变化可用Frenet-Serret公式表示：

(3)

式中：κ(s)、(s)分别为曲线的曲率和挠率，(s)|，=|dB/ds|，其中Δφ为曲线上相邻两点的切向量的夹角；Δφ为曲线上相邻两点的副法向量的夹角；Δs为相邻两点的弧长差.

曲率和挠率作为空间曲线的基本描述指标，前者表示曲线的切矢对于弧长的旋转速度，即曲线的弯曲程度；后者描述的是曲线的副法矢对于弧长的转动速度，即曲线的扭转程度；当挠率为0时，表示平面曲线.曲线上任意一点的Frenet标架变化情况可由该曲线的曲率、挠率唯一确定，即当给定曲率和挠率关于弧长的表达式及曲线的起点时，则曲线上的Frenet标架变化情况和曲线的几何形状也随之确定，如图2所示.

图2　κ(s)=0.5、(s)=0.5时的空间曲线

假设路线起点Ps为O(0,0,0)，以r(0)为原点对r(s)进行泰勒展开，可得到

(4)

取r(s)=[0,0,0]为计算弧长的始点，则曲线上距r(0)点弧长为s的临近点的新坐标为r(s)=(s,κs2/2,κs3/6).由此可知，公路三维线形设计时仅需确定曲率、挠率随里程变化的函数，即可确定公路三维线形的具体走向.

2　三维线形设计框架

(1)走廊带确定

采用航测、野外测量等方法提供地形、地质、水文等自然条件基本数据，以及沿线城镇、工矿企业等资源分布情况.通过勘察和分析，确定需绕避的地区，如不良地质、水文地段，环境及文物保护区域，以确定三维空间受限图(环境约束)，并用不同颜色标注以区分空间限制要求的高低，以便路线控制点选择和设计时，避免这些冲突区域.最终确定冲突最少的走廊带设计范围.

(2)设计速度确定

根据公路的功能、等级、交通量，并结合沿线地

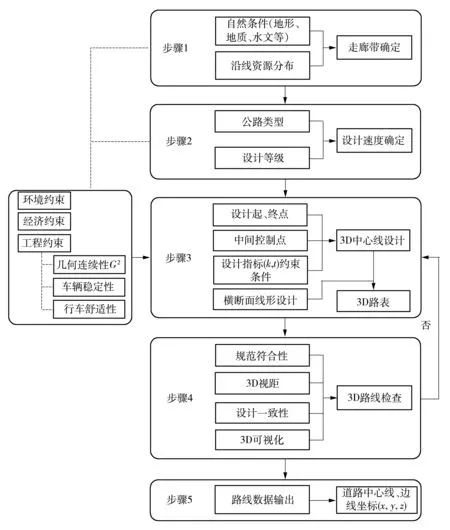
图3　公路三维线形设计框架

形、地质等状况，经论证确定路线的设计速度，以此确定设计指标工程约束条件确定的依据，以方便设计人员合理选取设计参数取值.

(3)3D路线设计

在路线起、终点确定的情况下，选择适宜的中间控制点进行路线设计.中间控制点选择时必须综合考虑路线规划、环境约束条件、关键构造物的限制以及填挖平衡等经济要求.路线设计过程中相关设计指标(曲率、挠率)的确定必须满足公路实际工程约束的要求，即在线形几何连续的前提下，保证车辆在给定设计速度行驶条件下的车辆稳定性和行车舒适性要求.并综合考虑工程经济性要求和实际需要，从中选取适当的路线设计方案初步完成3D路线设计.

(4)3D路线检查

3D路线初步设计完成后，根据预定的设计速度，检查相应的设计指标是否满足规范的相关要求；在此基础上对3D视距和设计一致性进行评估，结合3D可视化技术检查设计线形的安全性.当安全性不符合相关要求时，需对线形进行相应地设计和调整，直至满足相关要求为止.

(5)数据输出

在完成上述设计过程后，将设计出的三维路线转换成直角坐标系的参数方程形式，以方便实际的放样和施工.

3　工程约束条件建模

根据图3可知，公路三维线形设计时的一个关键性问题是设计参数曲率和挠率的确定.考虑到公路线形的一个基本要求是设计的线形应该是可行驶的，即应满足汽车的行驶特性和驾驶人员的需求，故在下文中主要从几何连续性、车辆稳定性和行车舒适性3个角度对公路三维线形设计指标的约束条件进行研究.

3.1几何连续性

连续性是对曲线外形规则程度的度量，连续的曲线视觉上是光滑、顺眼的.常用参数连续性或几何连续性来判定曲线的连续程度.相比于参数连续性，几何连续性(用Gn表示)，它摆脱了对参数选择的依赖性和非正则情况，侧重于曲线形状内在几何特征的描述，为形状定义与控制提供了额外的自由度，更便于人机交互设计.大量的观测研究表明，汽车行驶轨迹是一条连续的空间曲线，具有曲线、曲率及曲率变化率的连续性[14]，这也意味着汽车行驶轨迹在空间上是一条G3连续的曲线.根据曲率和挠率的定义，对不同平、纵线形单元组合形成的空间曲线的曲率和挠率进行计算和分析，汇总于表1.研究发现在这些空间组合曲线的连接点处，曲线的连续性存在不同程度的衰减.即使公路线形在平面和纵断面上都满足高阶几何连续(G2连续)，但在三维空间中，这种几何连续有可能衰减到低阶几何连续(G0、G1连续)，这在一定程度上影响了行车的平顺性和视觉流畅性.G2连续与G3连续视觉效果均非常好，但G3连续对曲线阶数要求更高，需消耗更多的计算资源，实际工业设计中并不常用.目前常用的几种几何连续阶数的计算及其几何意义汇总于表2.笔者通过大量的研究发现曲率和挠率的不连续与行车安全强相关，且曲率的连续对行车安全起主导作用[15].因此，综合考虑计算资源占用量大小、操作简易性和对行车安全影响的重要性，公路三维线形设计应至少保证G2连续性要求，即曲率连续，并通过局部设计修改来控制挠率的变化以实现更好的效果.

表1　不同平、纵线形单元组合下的空间曲率和挠率1)

1)表中kh表示平曲线半径；i表示纵坡.

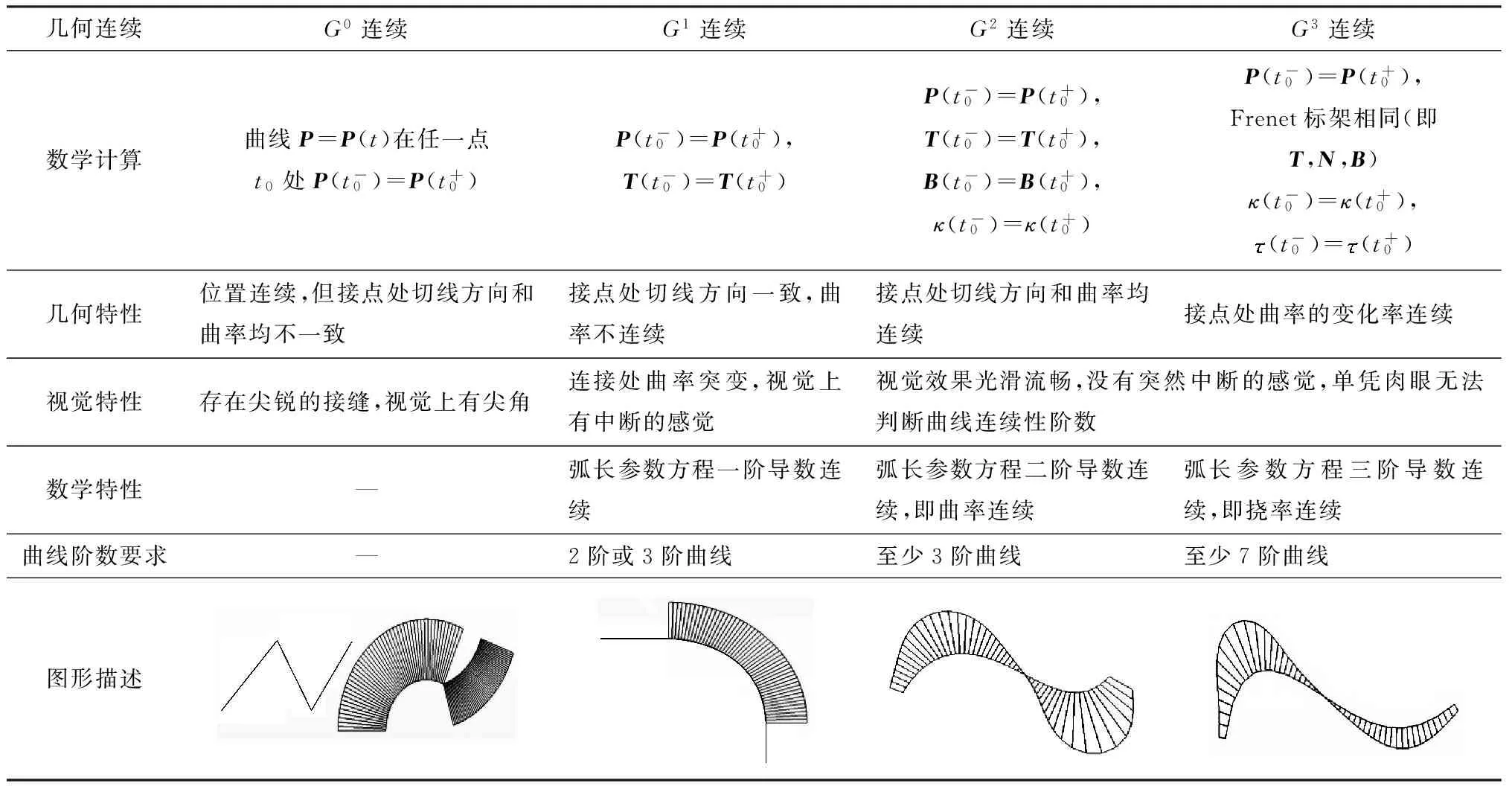
表2　曲线各阶连续性特征总结

3.2车辆稳定性

车辆稳定性是路线设计时保证汽车安全行驶的一个基本要求，也是传统设计方法中部分关键性的技术指标(如平曲线最小半径、超高等)确定的依据.在对车辆运动特性分析前，首先需建立相应的坐标系以构建车辆运动方程.如图4所示，研究分析时将车辆视为质量集中在重心(CG)上的对称刚体，以车辆重心为原点O′，建立车辆坐标系O′-X′Y′Z′.当车辆移动时，车辆坐标系也随之运动，其3个单位方向矢量构成了Frenet活动标架.当汽车重心的空间轨迹(即曲率和挠率)确定后，相应的汽车运动状态可随之确定.根据车辆动力学，可将汽车在笛卡尔坐标系中的运动转换至车辆坐标系中进行研究分析.在车辆坐标系中，汽车空间运动方程表示如下：

(5)

图4　汽车空间运动示意图

汽车在弯道上行驶时，车辆主要受到向下的重力G，路面施加给左右车轮的支持力NL、NR，以及左右侧车轮与路表作用产生的摩擦力fL、fR作用，假设路面横向倾角为θ.由力学知识可知，汽车行驶过程中不发生滑移应满足主法线方向(FN)和副法线方向(FB)的受力平衡：

(6)

式中：φ为路面横向摩阻系数；ih为超高横坡度，ih=tanθ.

车辆在设有超高的曲线段上行驶时，为使车辆不产生向外倾覆的危险，应满足

NLb=G(cosθ·b/2+sinθ·h)+maN(sinθ·b/2-

cosθ·h)≥0

(7)

化简后即得到

(8)

式中：b为汽车轮距，m；h为汽车重心高度，m.

综上可知，为保证汽车行驶的稳定性，三维路线设计时曲率应满足

(9)

3.3行车舒适性

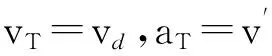
(10)

式中：aN,com,jN,com,jB,com分别为横向加速度、横向加加速度和竖向加加速度对应的行车舒适性阈值.

各国学者对驾驶员行驶过程中所能忍受的最大

加速度及加加速度进行了详细的研究，并提出了不同的舒适性阈值和评价标准[16].由于每个驾驶员个体对运动变化(振动)的敏感性不同，且缺少统一的测量和评估方法，目前并未建立统一的行车舒适性界限值.根据已有实测数据和现行路线形设计中关于行车舒适性的一般规定，文中确定了公路三维线形设计时行车舒适性的阈值分别为：aN,com=1.8m/s2，jN,com=0.6m/s3，jB,com=0.5m/s3.

3.4工程约束模型

(11)

考虑到现行公路线形设计规范中相关设计参数是考虑了上述约束条件和排水等其他要求，并经过多年工程实践不断修订完善得到他，而公路三维线形设计尚处于起步阶段，传统设计的经验累积对三维线形指标具有一定的参考价值，尤其是挠率指标的确定.故可根据表1中曲率、挠率与二维线形设计指标的关系，将现行路线设计规范中的相应参数约束转换为三维线形指标的约束，并结合式(11)建立的工程约束条件，最终确定不同设计速度下公路三维线形设计指标的取值应满足的约束要求，汇总于表3.

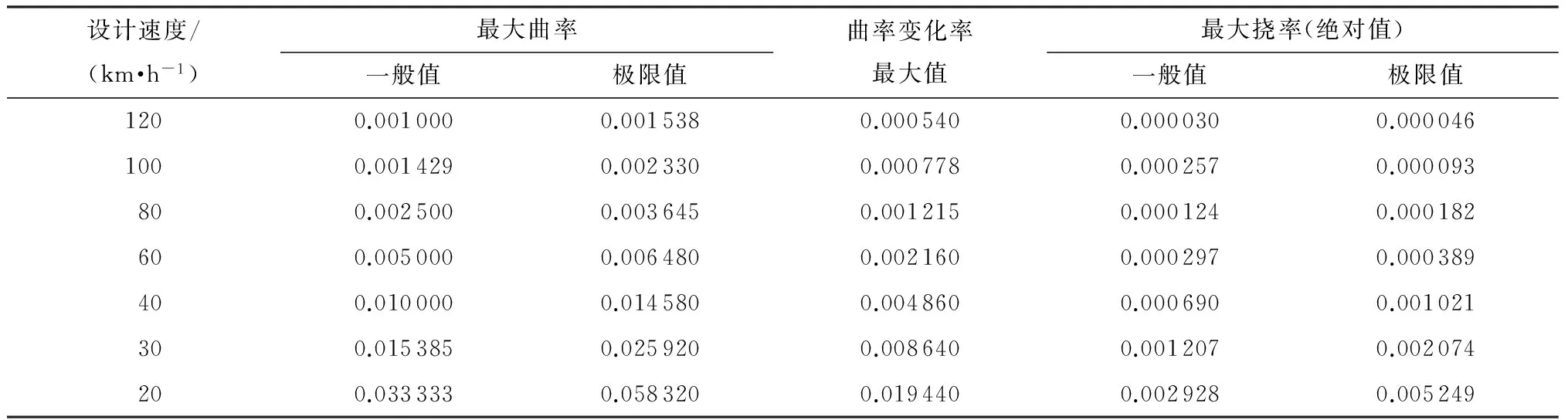
表3　不同设计速度下的三维线形设计指标值

4　结语

文中基于“公路中心线本质上是一条三维曲线”这一事实，从空间曲线几何特性出发，以弧长为设计参数，以空间曲线基本几何不变量曲率和挠率为设计指标，提出了新的公路三维线形设计方法和设计框架.新的三维线形设计指标避免了二维平、纵线形设计指标无法耦合和组合线形空间效果无法量化评估的不足，对提高公路设计水平和设计质量有积极意义.同时分别从几何连续性、车辆稳定性及行车舒适性3方面，对三维线形设计指标应满足的工程约束条件进行了分析，建立了相应的约束模型，结合现有设计规范和设计经验，最终确定了不同设计速度下三维线形设计指标取值应满足的参数约束条件，为后续的公路空间线形模型构建奠定了基础.

文中初步提出了三维线形设计的框架，但并未涉及具体的曲线形式构成，今后还需对路线曲线形式选择及构造进行研究.根据文中成果可知，应用于公路上的构造曲线应具有足够的连续性，至少应保证G2连续，即曲率连续，并满足构造简单、便于操作的要求.

[1]HASSAN Y,EASA S M,EL-HALIM A O.State-of-the-art of three-dimensional highway geometric design [J].Canadian Journal of Civil Engineering,1998,25(3):500- 511.

[2]符锌砂,龙立敦,李海峰,等.基于体感交互的公路真三维设计与系统架构 [J].华南理工大学学报(自然科学版),2014,42(8):91- 96.

FU Xin-sha,LONG Li-dun,LI Hai-feng,et al.Method and system architecture of true three-dimensional highway alignment design based on motion sensing interaction [J].Journal of South China University of Technology(Natural Science Edition),2014,42(8):91- 96.

[3]NG J C W,SAYED T.Effect of geometric design consistency on road safety [J].Canadian Journal of Civil Engineering,2004,31:218- 227.

[4]郭应时,付锐,袁伟,等.山区公路事故率与平面线形的关系 [J].交通运输工程学报,2012,12(1):63- 71.

GUO Ying-shi,FU Rui,YUAN Wei,et al.Relation between accident rate and horizontal alignment for mountain highway [J].Journal of Traffic and Transportation Engineering,2012,12(1):63- 71.

[5]孟祥海,关志强,郑来.基于几何线形指标的山区高速公路安全性评价 [J].中国公路学报,2011,24(2):103- 108.

MENG Xiang-hai,GUAN Zhi-qiang,ZHENG Lai.Safety evaluation of mountainous expressway based on geometric alignment indexes [J].China Journal of Highway and Transport,2011,24(2):103- 108.

[6]EASA S M,STRAUSS T R,HASSAN Y,et al.Three-dimensional transportation analysis:planning and design [J].J Transp Eng,2002,128:250- 258.

[7]CHENG J F,LEE Y.Model for three-dimensional highway alignment [J].J Transp Eng,2006,132:913- 920.

[8]《中国公路学报》编辑部.中国道路工程学术研究综述 2013 [J].中国公路学报,2013,26(3):1- 36.

Editional Department of China Journal of Highway and Transport.Review on China’s road engineering research:2013 [J].China Journal of Highway and Transport,2013,26(3):1- 36.

[9]MAKANAE K.Highway geometric modeling method by curvature and gradient functions [J].Conference of Product and Process Modeling,2002:463- 464.

[10]林声,郭忠印,周小焕,等.公路线形空间几何特性模型及其应用 [J].中国公路学报,2010,23(S1):47- 52.

LIN Sheng,GUO Zhong-yin,ZHOU Xiao-huan,et al.Models of highway alignment spatial geometric properties and their applications [J].China Journal of Highway and Transport,2010,23(S1):47- 52.

[11]KUHN W,KUBIK R,LEITHOFF I.Comprehensive three-dimensional methodology for design,assessment,and checking process of rural roads [C]∥Transportation Research Board 92nd Annual Meeting.Washington D C:TRB,2013:1- 13.

[12]屠书荣.关于样条曲线应用于公路平面线形设计几个问题的研究 [J].重庆交通学院学报,1994,13(5):66- 71.

TU Shu-rong.Study on application of spline to design of horizontal alignment of highway [J].Journal of Chong-qing Jiaotong Institute,1994,13(5):66- 71.

[13]OPREA J.Differential geometry and its applications [M].Cambridge:Cambridge University Press,2007.

[14]杨少伟.道路勘测设计 [M].第3版.北京:人民交通出版社,2009.

[15]符锌砂,葛婷,李海峰,等.基于公路三维线形几何特性的行车安全分析 [J].中国公路学报,2015,28(9):24- 29.

FU Xin-sha,GE Ting,LI Hai-feng,et al.Traffic safety analysis based on geometric properties of highway three-dimensional alignment [J].China Journal of Highway and Transport,2015,28(9):24- 29.

[16]AASHTO—2011.A policy on geometric design of highways and streets [S].Three-Dimensional Highway Alignment Design and Constraints Modeling

s: Supported by the National Natural Science Foundation of China(51278202，51378512,51508204)

GETing1,2FUXin-sha1LIHai-feng3LONGLi-dun1YANGYong-hong1

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China; 2.School of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, Jiangsu, China; 3. School of Geosciences and Info-Physics, Central South University, Changsha 410007, Hunan, China)

Highway geometric design is an important part of highway construction, which directly influences the safety and comfort of driving. In order to overcome the shortcomings of the separated horizontal and vertical alignment design methods, by adopting the curvature and the torsion as new alignment design indexes, a new method for the three-dimensional highway geometric design is developed based on the fact that the highway centerline is a three-dimensional curve in nature. Then, by analyzing the engineering constrains of the three-dimensional highway alignment design from the aspects of geometric continuity, vehicle stability and driving comfort, a constraint model is constructed. Finally, the design values of the three-dimensional alignment indexes at different design speeds are determined based on the current design guidelines and experiences and by integrating the constructed constraint model. This new design method can avoid the limitations of unmeasurable combined effects and geometric continuity degradation in the traditional design method, and it provides a new solution to improving the safety of highway alignment design.

road engineering; three-dimensional alignment design; curvature; torsion; geometric continuity; vehicle stability; driving comfort

2015- 09- 03

国家自然科学基金资助项目(51278202，51378512,51508204)

葛婷(1987-)，女，博士，讲师，主要从事道路线形设计理论与方法研究.E-nail:geting_happy@163.com

符锌砂(1955-)，男，教授，博士生导师，主要从事道路计算机辅助设计研究.E-mail:fuxinsha@163.com

1000- 565X(2016)08- 0091- 07

U 412

10.3969/j.issn.1000-565X.2016.08.014