数形结合“妙”解数学问题

刘天有

（山西省大同市左云县高级中学）

数形结合“妙”解数学问题

刘天有

（山西省大同市左云县高级中学）

数形结合是在数学解题过程中的一种重要解题思想，它是根据数与形之间的对应关系，通过数和形的相互转化解决数学问题的.数形结合的实质是将较抽象的数学语言和直观的图象结合起来，它可以使代数问题几何化，几何问题代数化，其应用包括两个方面：（1）把某些抽象的数学问题直观化、形象化，揭示数学问题的本质；（2）把直观图形数量化，使其更加精确.现整理如下题型供大家体会：

题型一：数形结合解决方程的根的个数问题

题型分析：本题属于新定义题型，需先写出（fx）的解析式，然后将方程（fx）=m的根的个数转化为求函数y=（fx）图象与直线y= m交点的个数.

作出函数f（x）的图象如图1所示.

图1

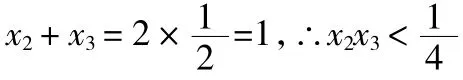
反思：研究方程根的个数、根的范围问题时，经常采用数形结合的思想，方程f（x）=0的根，就是函数f（x）的零点，方程f（x）=g（x）的根，就是函数f（x）和g（x）的图象交点的横坐标.

题型二 数形结合解决有明显几何意义的式子（概念）问题

而直线QA的斜率k=1，直线4a+2b-1=0的斜率为-2，显然不等式组所表示的平面区域不包括边界，所以P，Q连线的斜率的取值范围为（-2，1），故选D.

图2

反思：如果等式、代数式的结构蕴含明显的几何特征，就要考虑用数形结合的思想方法解题，即所谓的几何法求解.

题型三 数形结合解几何问题

例3.如图3，已知点P在抛物线y2=4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为（）

图3

题型分析：本题可以结合图形将抛物线上的点P到焦点的距离转化为到准线的距离，再探求最值.

解析：定点Q（2，-1）在抛物线内部，由抛物线的定义可知，动点P到抛物线焦点的距离等于它到准线的距离，问题转化为当点P到点Q的距离和点P到抛物线的准线距离之和最小时，求点P的坐标，显然点P是直线y=-1和抛物线y2=4x的交点时，两距离之和取最小值，解得这个点的坐标是（，-1），答案为A.

反思：在几何中的一些最值问题中，可以根据图形的性质结合图形上点的条件进行转换，快速求得最值.

纵观多年来的高考试题，巧妙运用数形结合的思想方法处理一些抽象的数学问题，可以起到事半功倍的作用，数形结合的重点是研究“以形助数”，把代数问题与图形紧密结合起来，可以使代数问题几何化，几何问题代数化.几何意义——两点（a，b），（-1，0）连线斜率求范围.

解：因为a＞0，所以二次函数f（x）的图象开口向上.

又f（0）=-1，所以要使函数f（x）的一个零点在区间（1，2）

熊云丰.巧用数形结合的思想解题［J］.才智，2008（24）.

·编辑杨国蓉