向量暗藏玄机利用向量确定二面角的大小

梁仕权

（贵州省息烽县第一中学）

向量暗藏玄机利用向量确定二面角的大小

梁仕权

（贵州省息烽县第一中学）

在高中数学教学中，求二面角是立体几何的重要组成部分之一。确定二面角的大小是高考的重点。二面角问题常转化为利用法向量夹角求解，它把空间问题转化为代数问题来解决。本文将从利用法向量与平面之间的关系，通过实例分析怎样利用法向量确定二面角大小。在确定二面角大小这一问题上，利用向量的基本原理，往往是通过两个半平面的法向量转化为线线直线所成的角的方法可以求二面角大小，并能通过这种方法有效地解决对二面角难以求解的问题，让学生充分体会到向量法在高中立体几何中的重要作用。但在求解立体几何的二面角问题时，确定二面角大小，采取的常用方法：在二面角α-I-β内，设分别为平面α，β的法向量，则α，β的法向量夹角的余弦值为

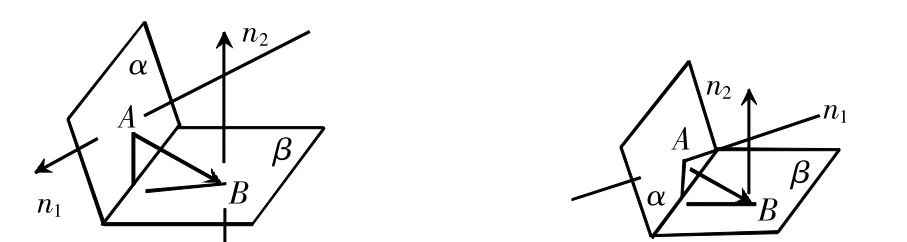
图1

二、利用向量法求解二面角的举例

例1.如图2，棱棱P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，PA=AB=，点E是棱PB的中点。

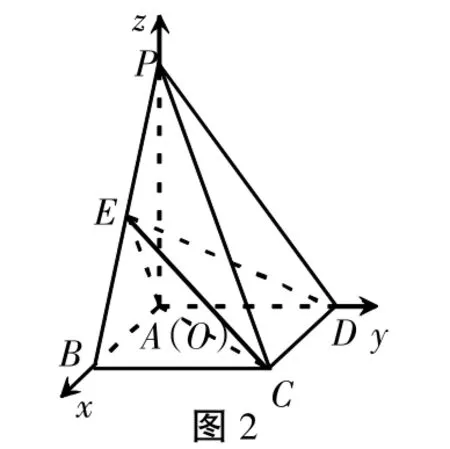
（1）证明AE垂直于平面PBC。

（2）求二面角B-EC-D的平面角的余弦。

在平面ECD内取一点D，在平面BCE内取B点，

例2.变式如图2四棱锥P-ABCD的底面是正方形PA垂直平面ABCD。

证明：无论四棱锥的高怎么变化，二面角B-PC-D总是大于90°。

证明：因PA⊥ABCD且底面ABCD为正方形，所以A为原点，建立如图2所示的空间空间坐标A-xyz，因底面为正方形ABCD，设正方形的边长AD=1，则A（0，0，0），B（1，0，0），C（1，1，0），D（0，1，0）

设OP=a，（a＞0），则P（0，0，a），∵BC⊥AB，PA⊥ABCD，BC⊥平面PAB，过A作AE垂直于PB，则AE⊥平面PBC，则有为平面PCB的一个法向量，且在平面PBA内，根据题意可设E（x，0，z）·=（1，0，-a）。

因D、B分别是平面PBC和平面PCD内的点，

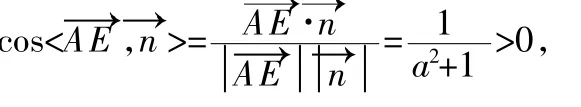
李秀兰.如何用空间向量求解二面角［J］.数量化学习：高中版，2011（3）.

·编辑李建军