基于双值参数化方法且考虑制造约束的炭纤维复合材料铺层优化

刘　哲，　金达锋,　范志瑞

(1.清华大学 汽车安全与节能国家重点实验室，北京100084；2.中北大学 机械与动力工程学院，山西 太原030051)



基于双值参数化方法且考虑制造约束的炭纤维复合材料铺层优化

刘哲1，金达锋1,范志瑞2

(1.清华大学 汽车安全与节能国家重点实验室，北京100084；2.中北大学 机械与动力工程学院，山西 太原030051)

基于梯度的优化方法对炭纤维复合材料层合板的铺层数量和顺序进行优化。优化问题中以铺层质量为目标，并以刚度和制造约束为约束。采用改进双值参数化方法对铺层的材料性能进行插值，并基于凸规划对偶算法对优化问题进行求解。为了适应凸规划对偶算法的特点，将关于铺层角度的制造约束表述为少量非线性约束。同时引入离散度约束和惩罚指数以消除优化结果中的中间变量。算例结果验证了该优化方法的有效性。

炭纤维复合材料； 制造约束； 优化； 层合板； 凸规划对偶算法

1　前言

由于炭纤维复合材料较钢、铝等材料具有较高的比强度、比刚度以及良好的抗腐蚀性，其在航空、航天等领域得到了广泛应用。炭纤维复合材料在力学性能上体现出较强的各向异性使得该种材料具有良好的可设计性。多数情况下为了使结构在满足一定刚度要求的情况下实现结构轻量化，对炭纤维复合材料的铺层层数和铺层角度的优化十分必要。

为了使铺层设计更具有工程意义，在铺层优化时还需考虑优化结果的可制造性、制造成本以及铺层在使用过程中随机载荷对铺层刚度和强度的影响。为此铺层优化的结果需满足相应的制造约束。在优化问题中引入制造约束虽然可能会影响优化结果的最优性，但是可以保证优化结果的可制造性、低成本以及在随机载荷下合理的刚度和强度。

Ghiasi[1]对近年来复合材料铺层优化方法做了系统性的综述。其中能够处理制造约束的优化方法主要包括遗传算法、分级优化方法和多材料拓扑优化方法。

由于遗传算法在处理整数型设计变量的优势，其在铺层优化中得到了广泛的关注[2-4]。研究者通过改进基因编码方式和遗传操作以及向优化问题中引入约束函数使得遗传算法具备处理制造约束的能力。但由于遗传算法的优化效率较低，其很难应用于铺层数量较多且铺层数量不确定的优化问题中。

Herencia[5]和Liu[6]等利用分级优化方法对铺层进行优化。在第一级优化中利用基于梯度的优化算法和铺层参数，找到最优的铺层参数。第二级优化利用遗传算法找到与最优铺层参数相对应的并且满足制造约束的实际铺层方案。此种方法在第一级优化中通过利用基于梯度的优化算法可以有效减少对目标函数和约束函数的计算次数并提高优化效率。在第二级优化中，虽然遗传算法的效率较低，但由于铺层角度与铺层参数的函数关系简单，故对优化效率影响不大。但是由于目前研究仅得出某些特定类型铺层对应的铺层参数可行域，此种方法具有较强的局限性。

Lund[7]基于多材料拓扑优化方法提出了离散材料优化方法(Discrete material optimization，DMO)对复合材料铺层进行优化。在此种方法中各铺层所采用材料的性能参数刚度是由各备选材料性能参数刚度的权重和所确定，各备选材料分别对应各备选铺层角度。在优化中将各备选铺层角度的权重值作为设计变量。同时，DMO方法采用基于SIMP法(Solid isotropic material with penalization)或RAMP法(Rational approximation of material properties)的材料插值公式对取中间值的设计变量进行惩罚。随后Bruyneel[8]提出了带惩罚形函数方法(Shape functions and parameterization，SFP)，该方法通过借鉴有限元方法中形函数的构造方式对材料插值公式进行改进。相对于DMO方法，SFP方法可有效减少设计变量的数量。但是当备选角度较多时该方法难以找到已有的形函数并构造相应的材料插值公式。Gao等[9]对SFP方法进行改进并提出双值参数化方法(Bi-valued coding parameterization，BCP)。BCP方法不再依赖于形函数构造材料插值公式，故备选角度可为任意数量，并且可用n个设计变量表示2n个备选角度。通过DMO、SFP和BCP方法建立的铺层优化问题可以通过基于梯度的优化算法进行求解，因此此类方法可以处理大规模的设计变量。但是如何将制造约束引入优化问题仍存在较大困难。

目前仅Sørensen[10]基于DMO方法就考虑制造约束的铺层优化问题进行了研究。其中通过引入大量的线性约束以表示制造约束，并采用序列二次规划算法对优化问题进行求解。由于在优化问题中存在过多约束，优化过程中存在设计变量的收敛速率较低的问题。

针对铺层层数较多、铺层层数可变且考虑制造约束的铺层优化问题，本文通过构造数量较少的非线性约束和对BCP方法的改进，提出了一种考虑制造约束的铺层优化问题的优化方法。针对以铺层质量为优化目标，结构刚度为约束并且考虑制造约束的铺层优化问题建立数学模型并基于凸规划对偶算法进行求解。

2　BCP方法介绍[9]

在BCP方法中，各铺层的材料性能为备选角度材料性能的权重之和，如式(1)所示。

(1)

式中,下标i为铺层层数编号，编号越大代表铺层越接近铺层底部；下标j为备选角度编号；D为材料的弹性矩阵；m为备选角度的数量；w为各备选角度的权重。

铺层内各备选角度的权重值如式(2)所示。

(2)

式中,mv为铺层角度设计变量的数量；xik为铺层角度设计变量，取值范围为[-1,1]；ρi为铺层密度设计变量，取值范围为[0,1]；p、q为惩罚指数；sjk为一系数，其表达式如式(3)所示。

(3)

铺层角度设计变量数目mv与备选角度数量m的关系如式(4)所示。

mv=[log2m]

(4)

当备选角度数量为4时，根据式(4)可知铺层角度设计变量数目为2。根据式(3)系数sjk的取值如表1所示。

根据式(2)和表1中的系数取值，四种备选角度的权重分布见图1。

表 1　系数sjk取值(mv=2,m=4)

图 1　备选角度权重分布图(mv=2,m=4,ρ=1,p=1)

3　制造约束介绍

为了保证铺层在随机载荷下的刚度、强度并降低制造成本，铺层设计需满足一定的制造约束。结合实际工程经验提出优化过程中所需满足的制造约束如下：

(1)为了降低制造成本，备选铺层角度需从{0°,+45°,-45°,90°}中选取，且各层厚度均相同；

(2)为了保证结构的可制造性，铺层的需具有连续性，即最底层铺层必须存在且两个确定存在的铺层之间不允许出现密度为0的铺层；

(3)为了在随机载荷下有效抑制裂纹在基体内的发展进而防止结构的失效，不允许出现连续n层及以上具有相同铺层角度的铺层，n通常取3或4。

图2和图3分别列举出违反制造约束2和制造约束3的铺层方案。图2中铺层4为最底层铺层，此时铺层4的密度为0违反了制造约束2中关于最底层铺层必须存在的要求。同时，在第1和3层铺层确定存在的情况下，处于二者之间的铺层2其密度为0。此种铺层方案违反了制造约束2中关于两个确定存在的铺层之间不允许出现密度为0铺层的要求。图3中四层铺层均存在，但1至3层的铺层角度均为同一确定角度，也即铺层中出现了连续3层铺层角度相同的情况。当n=3时，该铺层方案违反了制造约束3的要求。

4　优化问题的建立

优化问题以结构的质量作为优化目标，并以刚度和制造约束作为约束。当各层的面积、厚度和材料密度均相等时最小化铺层质量等价于最小化铺层层数。在优化过程中优化算法需对铺层的层数和各层的铺层角度进行优化。

图 2　违反制造约束2的铺层示意图

图 3　违反制造约束3的铺层示意图(n=3)

4.1改进BCP方法的设计变量

由于在优化中引入制造约束，BCP方法中部分设计变量并不适应此类优化问题，故需对BCP方法中设计变量进行改进。

保留BCP方法中的铺层角度设计变量。制造约束1中要求备选铺层角度数量为4，根据式(4)可知各层铺层角度设计变量数量为2。

在制造约束2中最底层铺层必须存在，因此在BCP方法中对应最底层铺层的密度在优化中应始终保持为1。如果优化过程中各层密度可自由变化则可能会违反制造约束2，因此需对各层密度值进行约束。可以通过要求铺层密度从底部至顶部逐层递减来满足制造约束2。将式(5)引入优化问题的数学模型后，虽然可使优化结果满足制造约束2，但由于向优化数学模型中引入过多的线性约束进而降低了使得优化问题的求解效率。

ρi-ρi+1≤0i=1,......,pn-1

(5)

式中,pn为铺层的总层数。

在此不再以BCP方法中各层密度值作为优化问题的设计变量，而是以相邻两层的密度值增量作为密度设计变量并记为xi3。为了便于区分，现将各层的密度值ρi称为物理密度。各层物理密度值ρi与密度设计变量xi3的函数关系见式(6)。当密度设计变量xi3≥0时，各铺层物理密度值均满足式(5)。

(6)

在优化过程中基于式(6)求得各铺层的物理密度后，将各层的物理密度和铺层角度设计变量代入式(2)后即可求得各铺层内所有备选铺层角度的权重。随后根据各备选铺层角度的权重求得各铺层内材料的弹性矩阵并代入有限元模型中求得结构响应。

图4为优化问题的设计变量以及各设计变量与铺层物理密度和角度的关系。由图4可知，除最底层铺层外每个铺层均包含一个密度设计变量和两个铺层角度设计变量，最底层铺层仅包含两个铺层角度设计变量。同时各铺层的铺层角度仅与各铺层相应的铺层角度设计变量相关，但各铺层的物理密度与其本身以及位于其底部铺层的密度设计变量相关。

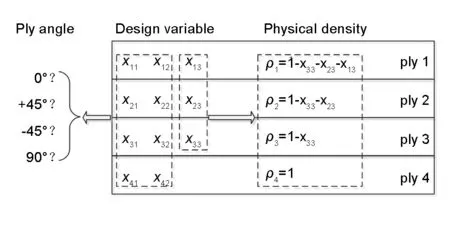
图 4　铺层优化设计变量示意图

4.2物理密度上限控制参数T

为了保证物理密度在相邻层之间的变化较为平缓，引入参数T对各层物理密度的上限进行控制。各铺层物理密度取值的上限是其底部相邻铺层物理密度值的分段函数,由图5和式(7)所示。参数T控制着两段线性函数的交点。在一定程度上参数T控制了铺层总层数的上限，并可使铺层质量集中于铺层的底部。式(8)为密度设计变量的下限值。

参数T的初值一般较小，并且在优化过程中采用连续化方法逐步增加参数T的值。表2给出当铺层层数为5且铺层底部两层的物理密度固定为1和0.95时，不同的参数T取值下其余各铺层的铺层密度上限值。

由表2可知，随着参数T的增加各铺层的物理密度上限值逐渐增加。当T=0.5时，各铺层的物理密度上限均相等且为0.95。

图 5　铺层物理密度上限示意图(T=0.1)

(7)

式中：

x13≥ρup(i+1)-ρupi

(8)

表 2　不同T下铺层物理密度上限值(ρ4=0.950, ρ5=1.000)

4.3最顶层铺层物理密度非负约束

由于没有设定密度设计变量的上限值，故存在密度设计变量取值较大并造成铺层物理密度小于0的情况出现。物理密度小于0的铺层并无实际意义，因此需要在优化问题中引入如式(9)所示的约束以保证最顶层铺层的物理密度值非负。

(9)

4.4目标函数及改进BCP方法的备选角度权重插值公式

在优化过程中，凸规划对偶算法不能保证约束不被违反。当铺层的物理密度为负值时会给优化带来问题。首先，式(2)中ρi的q次幂值可能为虚数并造成该铺层内各备选角度的权重值无实际物理意义。其次，如果将铺层的质量用各铺层的物理密度之和表示，则铺层的物理密度取负值更有利于降低目标函数的值。此种情况下不利于解的收敛，甚至使优化问题无法找到可行解。

为此需对目标函数和BCP方法中各备选角度权重插值公式进行改进并实现对中间密度有效的惩罚。目标函数可表示为各铺层物理密度绝对值之和。但由于绝对值函数连续不可导，则无法利用凸规划对偶算法对优化问题进行求解。因此可以通过构造一阶导数连续的函数来近似绝对值函数，如式(10)所示。

(10)

式中,ε为极小的正数。

同时，在权重插值公式内取消惩罚指数q，改进后的各备选角度权重插值公式如式(11)所示。

(11)

为了实现对中间密度的惩罚，将惩罚指数q引入铺层质量函数。各层质量相加即得到铺层的总质量如式(12)所示。

(12)

4.5制造约束3

在制造约束3中，不允许出现连续n层及以上具有相同铺层角度的铺层。该制造约束可表示为：

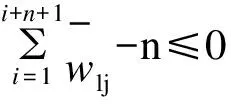
(13)

(14)

该函数是符号函数的连续化近似。因此可根据近似符号函数的输出对某一项约束是否被违反进行判断。为了使式(13)中约束满足时近似符号函数的输出为-1，将式(13)中的约束松弛为如式(15)所示。

i=1,2,...,pn-n-1

(15)

随后根据式(15)中各约束对应的近似符号函数的输出之和对铺层是否违反制造约束3进行判断。当且仅当式(15)中各约束均不被违反时，铺层方案才不违反制造约束3。因此各约束对应的近似符号函数的输出之和只有小于等于(n+1-pn)时，才能保证制造约束3不被违反。针对制造约束3需引入优化问题的约束如式(16)所示。

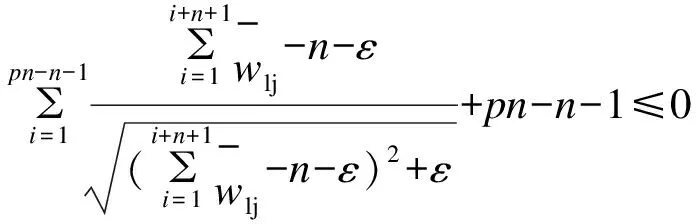
(16)

引入过滤函数分别对铺层的物理密度以及铺层角度设计变量进行过滤，使过滤后的变量更接近整数。随后用过滤后的铺层物理密度以及角度设计变量计算各铺层内各角度所对应的权重值，如式(17)所示。

(17)

基于Heaviside函数构造铺层物理密度的过滤函数，如式(18)所示。

(18)

式中，α1为过滤函数的阈值。

图 6　物理密度过滤函数在不同α1下的函数图像(β=10)

如图6所示物理密度过滤函数连续，且当β值较大时大部分物理密度在过滤后取值均为0或1。过滤函数的阈值α1控制着函数图像沿横轴的平移量。

过滤后物理密度对过滤前物理密度ρi的一阶导数如式(19)所示。

(19)

由式(19)可知，在ρi=α1处关于ρi的左导数等于右导数，则物理密度过滤函数一阶导数连续。同理可构造铺层角度设计变量过滤函数。如式(20)所示。

(20)

式中，α2为过滤函数的阈值。

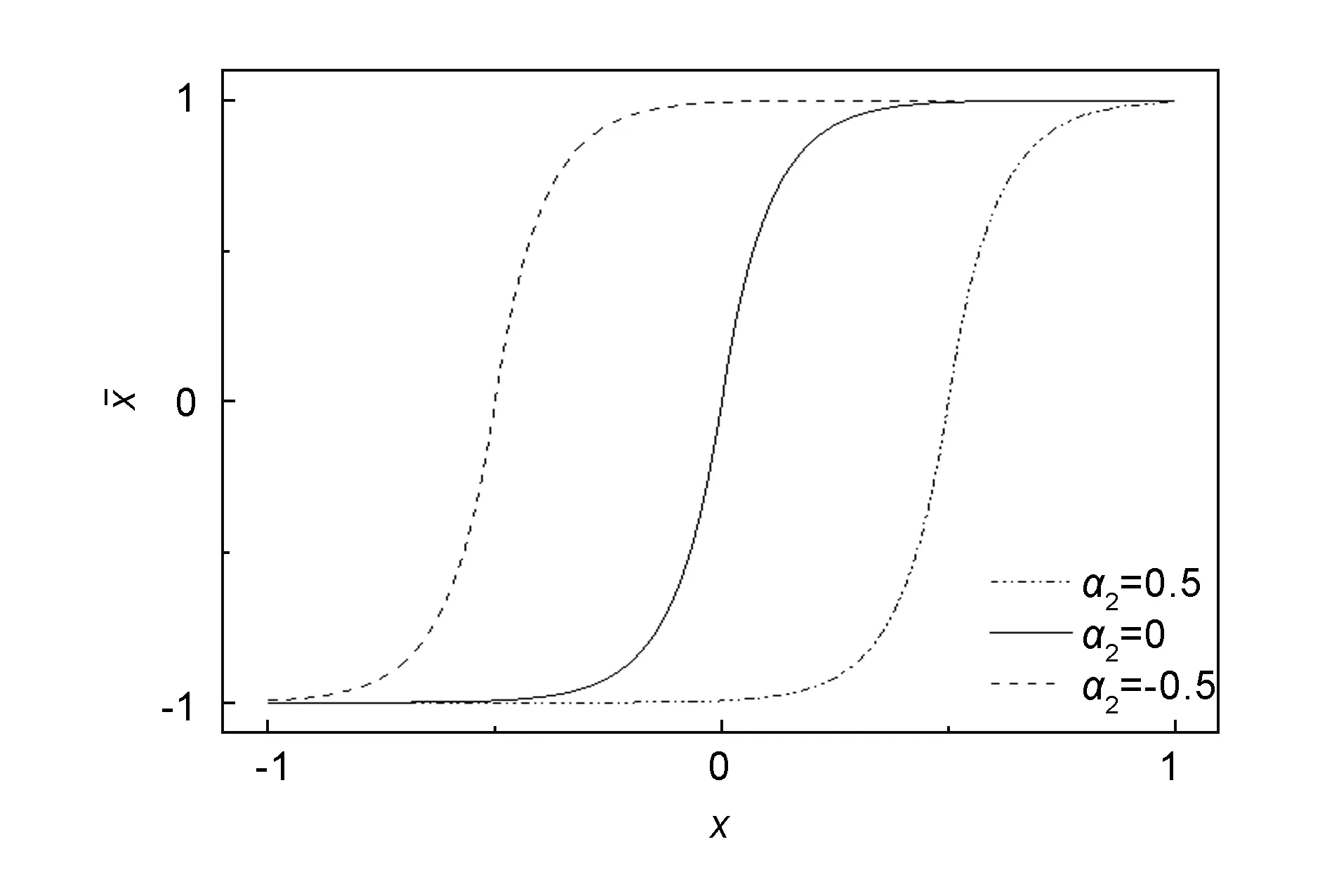
图 7　铺层角度设计变量过滤函数在不同α2下的函数图像(β=10)

如图7所示铺层角度设计变量过滤函数连续，且当β值较大时大部分变量在过滤后取值均为-1或1。过滤函数的阈值α2控制着函数图像沿横轴的平移量。

过滤后角度设计变量对过滤前角度设计变量xik的一阶导数如式(21)所示。

(21)

由式(21)可知，在xik=α2处关于xik的左导数等于右导数，则铺层角度设计变量过滤函数一阶导数连续。

4.6铺层角度设计变量离散度约束

在实际优化中仅依靠惩罚指数p很难保证铺层角度设计变量最终收敛至1或-1。因此有必要在优化问题中引入相关约束以消除铺层角度设计变量中的中间变量。为了衡量铺层角度设计变量偏离1和-1的程度，引入离散度概念并利用其构造相关约束。对于某一铺层的角度设计变量而言，其离散度的计算公式如式(22)所示。

(22)

式中,Mndi为第i层铺层角度设计变量的离散度；Mndik为第i层铺层第k个角度设计变量的离散度。

当xik=0时，Mndik为1且为最大值；当xik=-1或xik=1时，Mndik为0且为最小值。因此Mndi的最大值为且最小值为0。根据离散度函数的特点，对离散度函数的上限进行约束，如式(23)所示。

(23)

式中,Mndup为铺层角度设计变量离散度上限值。

在实际优化过程中，为防止优化结果过早地收敛至局部最优解，需采用连续化方法逐渐减少铺层角度设计变量离散度上限Mndup的值。

4.7优化数学模型

对于铺层优化问题，优化变量为密度设计变量和铺层角度设计变量，优化目标为铺层质量如式(12)所示，其约束包括结构柔顺度、式(9)、式(16)和式(23)。

find{xik}(i=1,...,pn;k=1,...3)

s.t.F=Ku

C-Cmax≤0

(24)

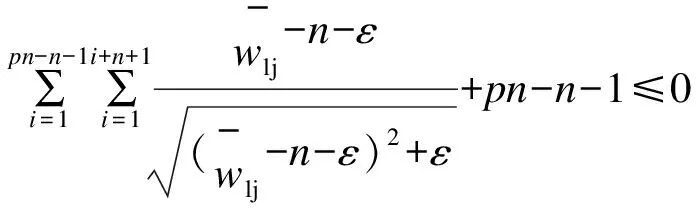
-1≤xi1≤1-1≤xi2≤1xi3≥ρup(i+1)-ρupi

式中,F为节点力向量；K为结构刚度矩阵；u为节点位移向量；C为结构柔顺度；Cmax为结构柔顺度上限值。

5　优化流程

本文优化问题的求解基于凸规划对偶算法，该算法可对多变量、少约束、高度非线性的优化问题进行高效率地求解。为了防止优化问题的解过早地收敛于局部最优,在优化过程中采用连续化方法对参数q、p、T以及Mndup的值进行改变。

在迭代初期铺层总层数的范围以及最优铺层角度均不确定，此时如果对铺层物理密度以及铺层角度设计变量的离散度提出较高的要求会造成过早收敛于局部最优解或无法收敛的情况。因为参数T控制各层物理密度的上限，所以在此阶段应首先确定参数T的大致范围。在大致确定了铺层的总层数并使得结构刚度以及各制造约束得到满足后，逐渐提高对铺层物理密度以及铺层角设计变量离散度的要求，并直至参数q、p以及Mndup达到预定的上限或下限为止。需要注意的是，随着对离散度要求的提高，结构刚度通常会相应降低。当结构刚度下降明显时，铺层总层数也需相应增加，因此参数T的值也需要继续随着结构刚度的变化而改变。

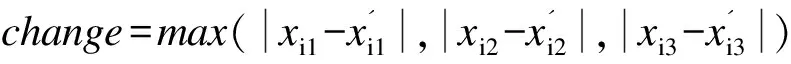
(25)

综上所述，优化流程如图8所示。

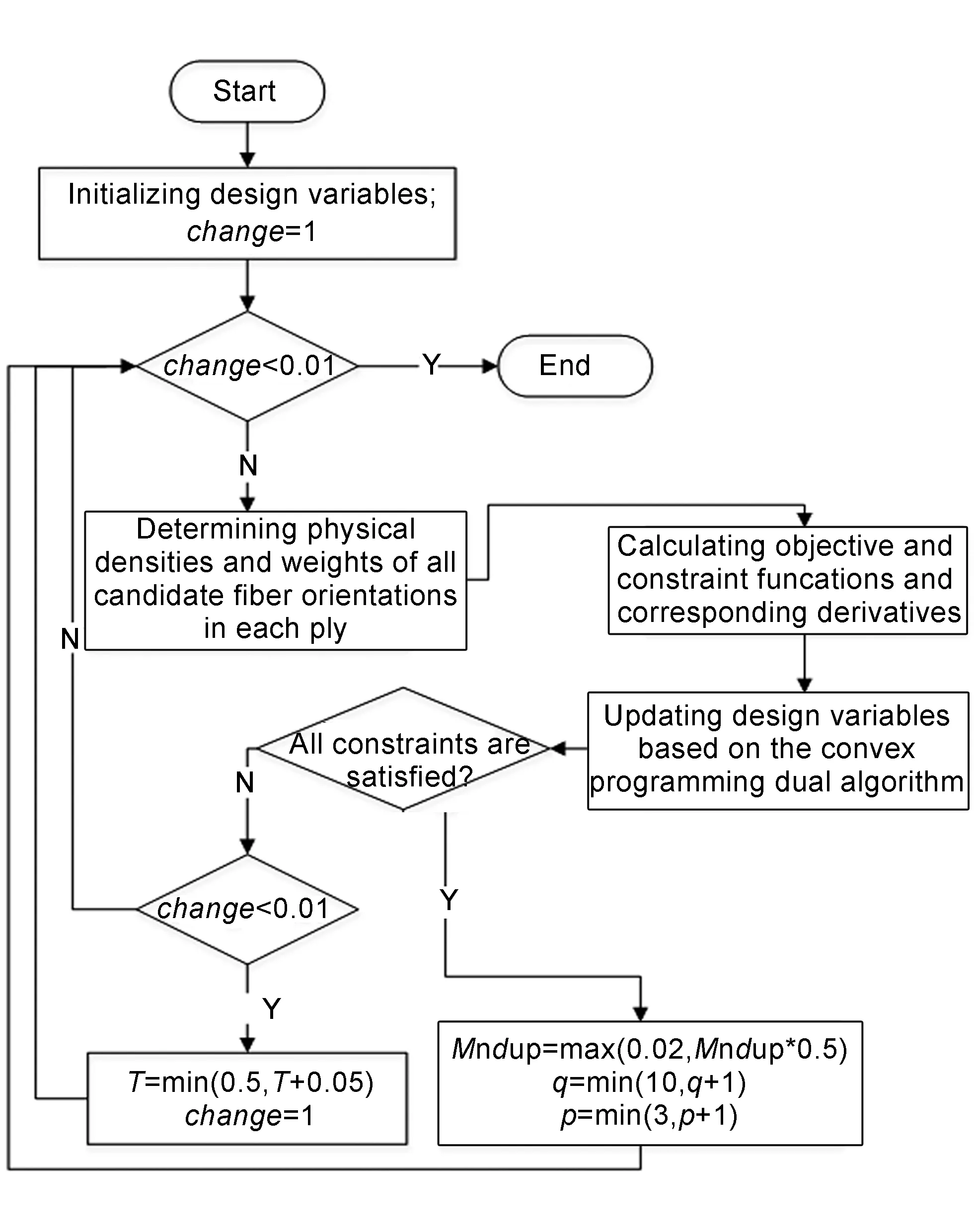
图 8　优化流程示意图

6　数值算例

算例对两种不同问题进行优化，各算例的载荷、边界条件以及几何尺寸分别见图9和图10。各数值算例中所采用的材料均相同，材料性能如表3所示。

所有算例的有限元分析均基于有限元软件ABAQUS完成，在有限元模型中选取四节点减缩积分壳单元S4R。单个铺层层厚为0.125 mm。优化流程的剩余步骤均基于MATLAB完成。

图 9　算例1几何尺寸、载荷及边界条件示意图

图 10　算例2几何尺寸、载荷及边界条件示意图

PropertiesValuesLongitudinaltensilemodulus162GPaLongitudinalcompressivemodulus145GPaTransversetensilemodulus9．2GPaTransversecompressivemodulus9．5GPaIn⁃planeshearmodulus5．0GPaPoisson＇sratio0．3

所有算例中参数q、p、Mndup以及T的初值均相同且取值为：q=1，p=1，Mndup=1，T=0.1。式(18)和式(20)中过滤函数的过滤阈值α1和α2分别为0.5和0，极小正数ε取0.001，β取5。n取值为3，备选角度为{0°,45°,90°,-45°}，备选角度与铺层角度设计变量的对应关系见图11。

铺层角度设计变量初始值均取0，也即不偏重于任何一个备选角度。铺层密度设计变量的初值取参数T初始值对应的铺层密度设计变量的上限值。

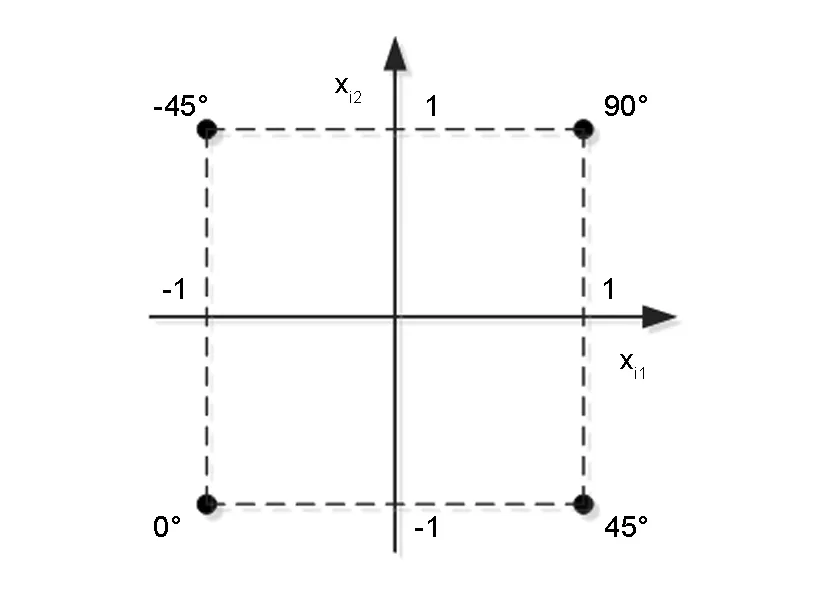
图 11　备选角度编码示意图

算例1中，柔顺度的上限Cmax分别取1×10-3J和6×10-4J，分别针对两种柔顺度上限进行优化，其优化结果见表4。

表 4　算例1优化结果

迭代终止时所有约束均满足，且优化结果的结构柔顺度值均等于相应柔顺度上限值。相关优化参数的取值见表5。

表 5　算例1中优化参数最终取值

算例2中，柔顺度的上限Cmax分别取5×10-3J和2×10-3J，分别针对两种柔顺度上限进行优化，其优化结果如表6所示。

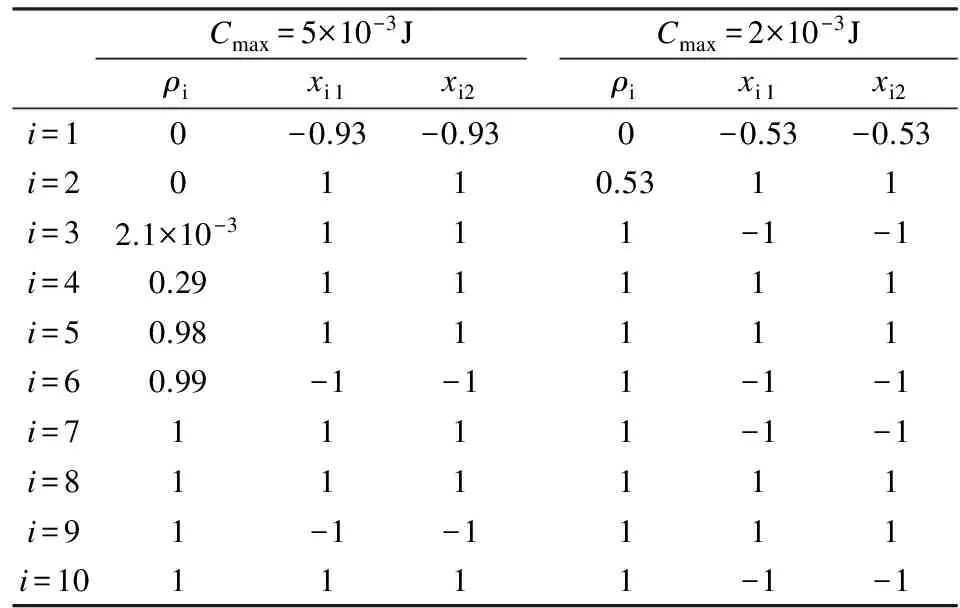
表 6　算例2优化结果

迭代终止时所有约束均满足，且优化结果的结构柔顺度值均等于相应柔顺度上限值。相关优化参数的取值如表7所示。

表 7　算例2中优化参数最终取值

根据各算例的优化结果可知，大部分铺层的物理密度值为0或1，也即明确了铺层的有无。虽然目标函数中的惩罚指数q对中间密度有惩罚作用，但是对于某一柔顺度上限值其通常对应的理论最优铺层层数并非整数，因此在优化结果中通常会出现在铺层物理密度值0和1的过渡区域存在物理密度为中间值的铺层。

由于将相邻两层物理密度之差作为优化设计变量，因此所有算例中铺层的物理密度从底部到顶部呈现递减趋势且满足式(5)。优化结果中避免出现夹空层的现象出现。同时，最底层铺层的物理密度在优化过程中为定值1进而保证了最底部铺层必须存在的要求。

除算例1中针对Cmax=6×10-4J的优化结果外，其余算例中铺层角度设计变量离散度上限值Mndup均减少至0.02。此种情况下除铺层物理密度为0的铺层外，其余铺层对应的铺层角度设计变量均接近-1或1，即可明确地得到相应铺层的铺层角度。

对于算例1，文献[10]在不考虑制造约束的前提下进行了铺层优化，最终得到各层的最优铺层角度均为0°。通过枚举法验证了解的最优性。根据表4所示各层的铺层角度设计变量值可知，优化结果中大部分铺层的铺层角度为0°，其中还存在少量铺层角度为90°的铺层。90°铺层存在的主要目的在于防止连续3层或3层以上0°铺层的出现。对于算例2，由表6可知最优铺层角度以90°为主，优化结果中存在的0°铺层主要目的是防止连续3层或3层以上90°铺层的出现。因此，该优化方法在保证铺层方案满足制造约束的同时有效地优化了铺层角度。但需要注意的是解的最优性并不能得到保证。

7　结论

以相邻层的密度增量作为铺层密度设计变量可有效避免优化结果中出现夹空层的现象；控制参数T和目标函数的构造保证物理密度在相邻层之间的变化较为平缓且有效消除了中间物理密度；引入关于铺层角度的非线性制造约束和铺层角度设计变量离散度约束保证了优化结果中出现明确且满足制造约束的铺层角度。

[1]Ghiasi H, Pasini D, Lessard L. Optimum stacking sequence design of composite materials Part I: Constant stiffness design[J]. Composite Structures, 2009, 90(1): 1-11.

[2]Liu B, Haftka R T, Akgün M A, et al. Permutation genetic algorithm for stacking sequence design of composite laminates[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(2): 357-372.

[3]Hansel W, Treptow A, Becker W, et al. A heuristic and a genetic topology optimization algorithm for weight-minimal laminate structures[J]. Composite Structures, 2002, 58(2): 287-294.

[4]Toropov V V, Jones R, Willment T, et al. Weight and manufacturability optimization of composite aircraft components based on a genetic algorithm[P]. 6th World Congresses of Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazil, 2005, 30.

[5]Herencia J E, Weaver P M, Friswell M I. Optimization of anisotropic composite panels with T-shaped stiffeners including transverse shear effects and out-of-plane loading[J]. Structural and Multidisciplinary Optimization, 2008, 37(2): 165-184.

[6]Liu D, Toroporov V V, Querin O M, et al. Bilevel optimization of blended composite wing panels[J]. Journal of Aircraft, 2011, 48(1): 107-118.

[7]Lund E, Stegmann J. On structural optimization of composite shell structures using a discrete constitutive parametrization[J]. Wind Energy, 2005, 8(1): 109-124.

[8]Bruyneel M. SFP a new parameterization based on shape functions for optimal material selection: Application to conventional composite plies[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 17-27.

[9]Gao T, Zhang W, Duysinx P. A bi-value coding parameterization scheme for the discrete optimal orientation design of the composite laminate[J]. International Journal for Numerical Methods in Engineering, 2012, 91(1): 98-114.

[10]Sørensen S N, Lund E. Topology and thickness optimization of laminated composites including manufacturing constraints[J]. Structural and Multidisciplinary Optimization, 2013, 48(2): 249-265.

Ply optimization of carbon fiber-reinforced plastics laminates based on a gradient-based optimization method with manufacturing constraints

LIU Zhe1,JIN Da-feng1,FAN Zhi-rui2

(1.StateKeyLaboratoryofAutomotiveSafetyandEnergy,TsinghuaUniversity,Beijing100084,China;2.SchoolofMechanicalandPowerEngineering,NorthUniversityofChina,Taiyuan030051,China)

We optimized the number of plies and the stacking sequence of carbon fiber-reinforced plastics laminates using a gradient-based optimization method. To attain industrial relevance and reduce the risk of failure and the cost, certain manufacturing constraints were considered in the optimization. Manufacturing constraints were: 1) candidate fiber orientations were limited to a finite set, 2) the bottom layer must be solid; 3) an intermediate void was not allowed, and 4) two or three identical contiguous layers were allowed at most. In the optimization, the mass was minimized with stiffness and manufacturing constraints. In order to avoid introducing linear constraints to the optimization model, a material property interpolation scheme called a bi-value coding parameterization scheme was modified and the manufacturing constraints concerning fiber orientation were expressed as nonlinear constraints. Meanwhile, a dispersion constraint and penalty index were introduced to eliminate intermediate variables. The optimization problem was solved by a convex programming dual algorithm. Numerical examples validate the optimization method.

Carbon fiber composite; Manufacturing constraint; Optimization; Laminates; Convex programming dual algorithm

JIN Da-feng, Ph. D, Associate Professor. E-mail：Jindf@tsinghua.edu.cn

introduction: LIU Zhe, Ph. D Candidate. E-mail：lz880818@hotmail.com

1007-8827(2016)01-0068-09

TB330.1

A

2015-11-29；

2016-01-14

金达锋，博士，副教授. E-mail：Jindf@tsinghua.edu.cn

刘哲,博士生. E-mail：lz880818@hotmail.com