一类新p-群的自同构群的最佳下界

班桂宁，田　甜，王玉琪

(广西大学数学与信息科学学院，广西南宁　530004)

一类新p-群的自同构群的最佳下界

班桂宁，田甜*，王玉琪

(广西大学数学与信息科学学院，广西南宁530004)

本文得到了中心非循环且中心商同构于p6阶第十四家族的新的有限p-群结构，运用群扩张理论和自由群理论证明了新群的存在性，特别的，证明了此类群为LA-群。

自同构群；阶；自由群；LA-群

关于有限p-群的自同构群阶的最佳下界，目前并没有得到最终的解决，但是与其息息相关的有一个著名的猜想，称为LA-猜想:设G为有限非循环p-群，且称满足LA-猜想的群为LA-群。该猜想对于自同构群阶的最佳下界给出了较好的回答，许多群论学者也为此做了很多研究。Davitt在文献[1]中提出满足中心商小于等于p4的有限非循环p-群G是LA-群；后来，在文献[2-7]中很多学者得到了中心商小于等于p5的有限非循环p-群G亦是LA-群。本文立足于前人的研究，选取文献[8]中p6阶群中第十四家族进行研究，利用亚循环群的幂结构公式，排除一些不存在群G，使得G/Z(G)≅H的p6阶群H；然后，给出存在中心商与十四家族群同构的新的p-群的结构，并利用群扩张理论和自由群理论证明其存在性；最后，运用自同构群的阶的性质证明其是满足LA-猜想的群，进而估算出新群的自同构群阶的最佳下界。

本文中的p是奇素数，PN-群是非交换的且没有非平凡交换直积因子的 p-群，文中所给出的a(i，l)，kl等参数如无具体说明均是正整数，符号Φ14(222)，Ac(G)等术语和其他符号都是标准的，详细可以参考文献[8]和[9]。

1　相关引理

引理1[1]设G/Z(G)＝，如果群H包含元素h和生成子集S，使得S中的每个元素的某一个相同次幂都等于h，则不存在群G，使得G/Z(G)≅H。

引理2[7]设如果群H中包含元素h和生成子集S，使得S中的每个元素的某一个相同次幂都等于h，则[h，H]＝1，h∈Z(G)。引理3[9]设G是群，a，b，c∈G，则

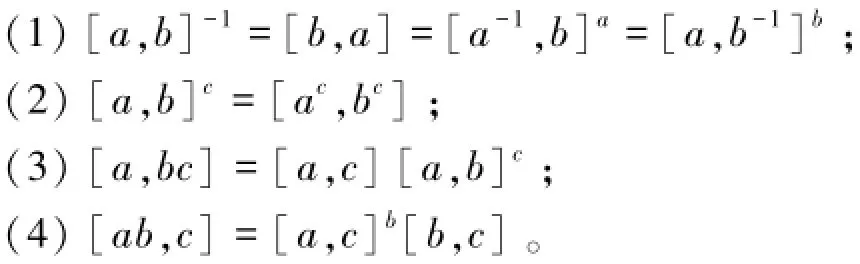
引理4[8]设G是群，a，b∈G，且[a，b]∈Z(G)，n为正整数，则

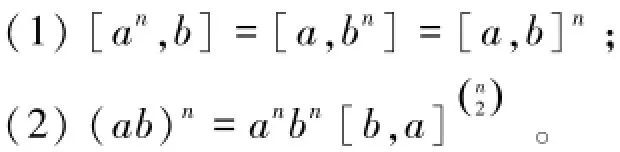
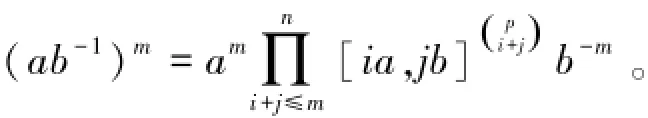
2　主要结果

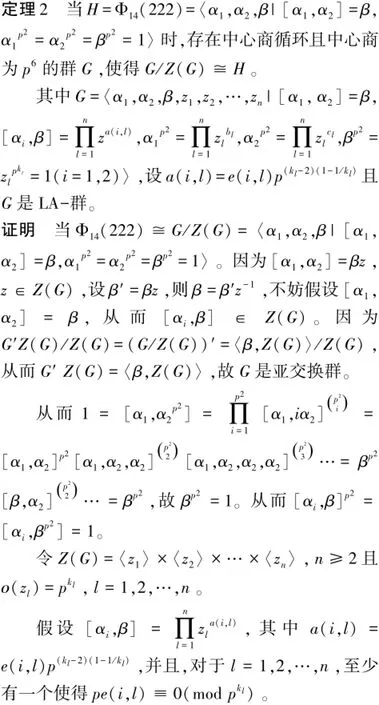
根据上述关系，利用群扩张理论和自由群理论证明定理中所给的群G是存在的并且满足其定义关系。我们分下面两步进行:

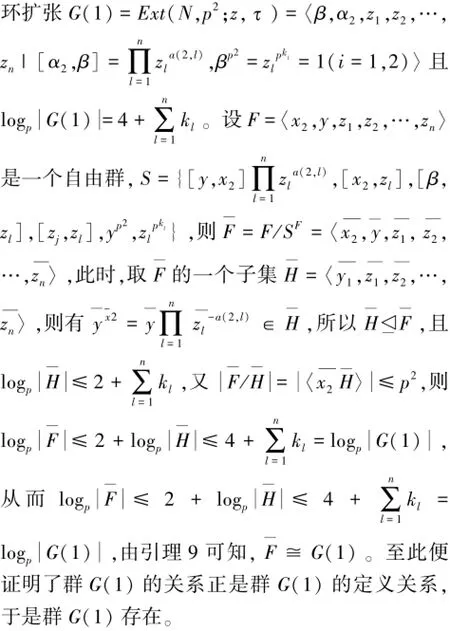
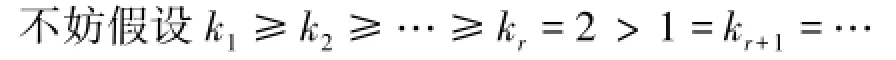
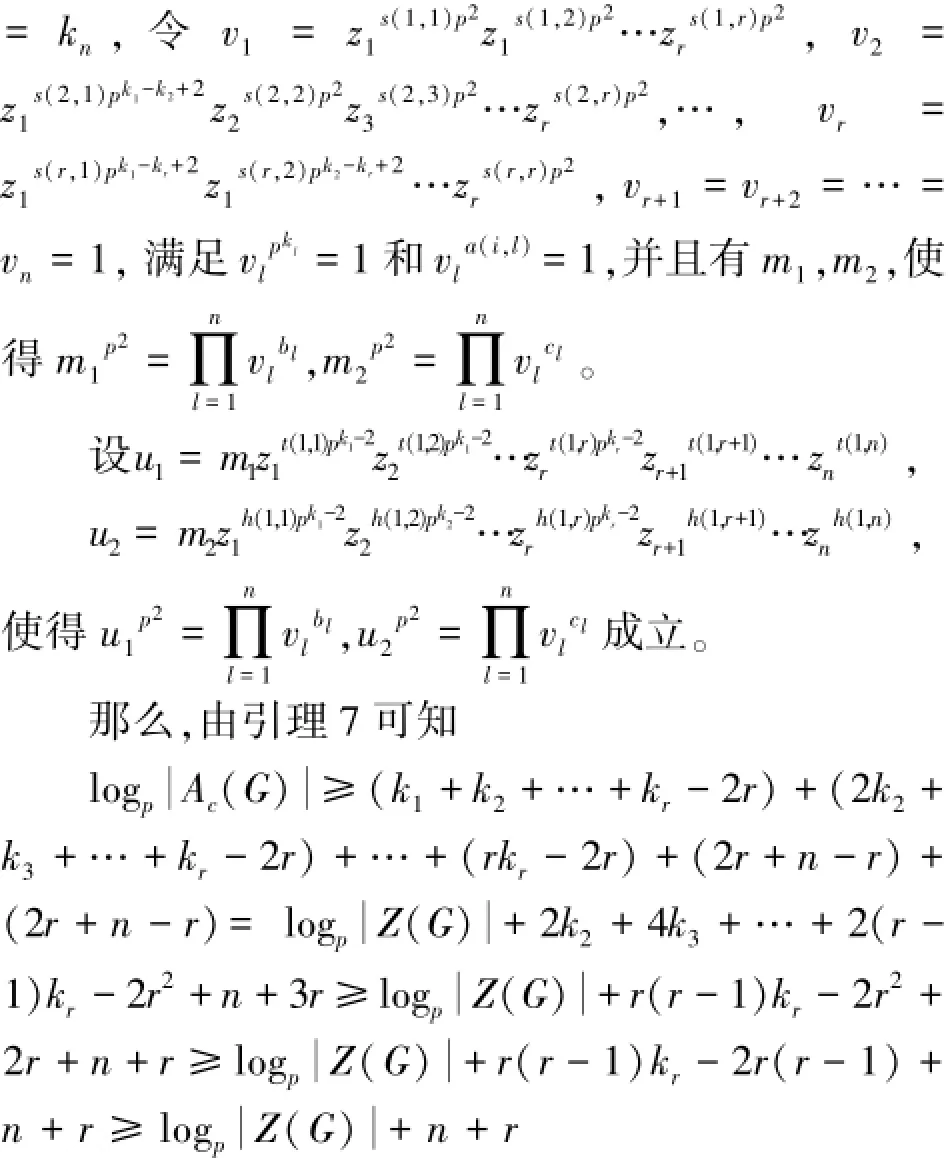
[1]Davitt R M.On the automorphism group of a finite p-group with a small central quotient[J].Canadian Journal of Mathematics，1980， 32(5):1168-1176.

[2]俞曙霞，班桂宁.若干LA-群及相关定理[J].广西大学学报(自然科学版)，1993，18(1):6-13.

[3]俞曙霞，班桂宁.关于LA-群的一个定理[J].广西大学学报(自然科学版)，1994，19(1):10-17.

[4]俞曙霞，班桂宁.具有中心循环和小中心商的有限p-群[J].广西大学学报(自然科学版)，1993，18(3):15-23.

[5]Ban G N，Zhang J S，Yu S X.The lower bound for the order of the automorphism groups[J].Proceeding of the Royal Irish Academy，1996，96A(2):159-167.

[6]张艳.关于Davitt一个重要结论的推广及相关研究[D].南宁:广西大学，2012.

[7]朱彩凤.关于 LA-猜想的若干问题研究[D].南宁:广西大学，2012.

[8]James R.The Groups Of Orderp6(pan odd Prime)[J].Mathematics of Computation，1980，34(150):613-637.

[9]徐明曜.有限群导引(上、下)[M].2版.北京:科学出版社，2011.

[10]Ban G N，Yu S X.Minimal Abelian groups that are not automorphism groups[J].Archivder Mathematik，1998，70(6):427-434.

[11]刘海林.若干中心循环且中心商群的阶为p6的LA-群[D].南宁:广西大学，2014.

[12]班桂宁，俞曙霞.一类p-群的自同构群的阶[J].数学学报，1992，35(4):570-574.

[13]Otto A.Central automorphisms of a finite p-group[J].Duke Mathematical Journal，1966，125:280-287.

[14]Hummel K G.The order of the automorphism group of a central product[J].Proceedings of the American Mathematical Society，1975，47:37-40.

(责任编辑:曾晶)

The Low Boundary of the Automorphism of A Class of New-group

BAN Guining，TIAN Tian*，WANG Yuqi
(School of Mathematics and Information Sciences，Guangxi University，Nanning 530004，China)

A new finite group was given，whose center is non-cyclic and the central quotient is isomorphic to which order is；then，the existence of the new group was proven by extension theory of group and free group theory；especially，the new group is LA-group was investigated.

automorphism group；order；free group；LA-group

O152.1

A

1000-5269(2016)01-0001-04DOI:10.15958/j.cnki.gdxbzrb.2016.01.01

2015-09-27

国家自然科学基金(61074185)；广西自然科学基金(0832054)

班桂宁(1962-)，男，教授，博士，研究方向:群论，信息安全，控制论，Email:banguining101＠sina.com.

田甜，Email:ltnco＠sina.com.