面向复杂地形的四足机器人步态生成方法

陈雅辉，谭跃刚，李 彰

(武汉理工大学 机电工程学院，湖北 武汉 430070)

面向复杂地形的四足机器人步态生成方法

陈雅辉，谭跃刚，李 彰

(武汉理工大学 机电工程学院，湖北 武汉 430070)

为实现四足机器人在凹凸地形上稳定运动并能选择最大步长的目的，提出了基于稳定裕度的步态规划方法;基于研究对象，建立四足机器人的运动学方程及逆运动学方程，将机器人足端的位置映射为各关节的关节变量；提出工作空间矩阵的概念，将所需克服的地形高度反映到工作空间矩阵中，并选择最优步态区域；依据四足机器人的立足点在质心坐标系下的空间坐标，以纵向稳定裕度为约束条件，在工作空间矩阵中计算机器人摆动腿的最大步长并规划机械腿的运动轨迹；针对所提出的方法，分别利用MATLAB和ADAMS进行仿真验证;在MATLAB环境中计算并验证质心的水平投影是否在立足点形成支撑多变形内，而ADAMS平台分析机器人在复杂地形上的位移变化及姿态变化。仿真结果表明机器人的质心始终在支撑多边形内，机器人的躯干姿态基本保持不变且运动速度匀速，所提出的方法能够保证机器人稳定行走，为四足机器人的稳定运动提出依据。

四足机器人；慢走步态；工作空间矩阵；运动规划

0 引言

相对于轮式机器人和履带式机器人而言，足式机器人因其运动方式及支撑方式的不同，具有运动离散性，较强的环境适应性和灵活性。足式机器人在物料运输、抢险救灾、娱乐等方面具有强大的潜在应用前景。在众多类型足式机器人中，四足机器人结构简单、稳定性较好，成为国内外研究的热点[1]。自波士顿动力公司研发出军用运输机器人Bigdog[2]以来，因其强大的负载能力和优秀的运动能力，再次引起四足机器人研究热潮。

目前，四足机器人的运动研究主要朝着高速化，高适应性方向发展。高速化研究旨在提高四足机器人的运动速度，主要是从结构，控制算法及步态研究三个方向展开研究，其代表有MIT研制的Cheetah机器人，其运动速度已达30 km/h。高适应性研究主要目的是提高四足机器人对复杂地形的适应性，目前主要是从姿态控制策略及步态研究两个方向进行研究，具体分为两个方向：第一，在四足机器人运动过程中如何调整四足机器人的姿态，并实现快速控制。Dimitris[3]等人通过调整机器人躯干的运动轨迹，使质心的水平投影始终在机器人支撑多边形范围内，实现四足机器人稳定行走。鄂明成[4]等人利用弹簧阻尼模型，以各足等效力矩相等为平衡条件，躯干的俯仰角和翻滚角为边界条件，调整躯干的姿态，使四足机器人在运动过程中尽量保持支撑力均等。Raibert[5-6]使用虚拟腿模型，实现单足机器人Hopper的稳定控制。Tran[7]和Havoutis[8]建立四足机器人的虚拟弹簧-阻尼单腿模型，规划主动柔顺步态，使机器人顺利通过崎岖地形并且具有抵抗侧向冲击力的能力。第二，四足机器人如何寻找合适的立足点。Hirose学者[9-10]提出用于寻找立足点的对角线原理，成功规划四足机器人的爬行步态。Mostafa Ajallooeian[11]基于非线性算法的CPG，修正四足机器人的落脚点和肢体伸展长度，实现四足机器人能够在崎岖的路面上平稳行走。Shaoping Bai[12]利用非规则步态补偿规则步态的方法来提高规则步态对非结构化环境的适应能力。通过根据障碍物的大小调整步距，抬腿高度等步行参数提高机器人的步行效果。王恒升[13]和刘冠初[14]等人的步态规划方法与Shaoping Bai相似，将水平方向的工作范围分割成多段相同的区域，根据障碍物的大小，选择有效节点。华中科技大学陈学东等人[15]提出了稳定区域的概念，并利用它规划出四足机器人的立足点。目前所提出步态规划方法大部分都是通过先脱离机械结构来计算出立足点范围，然后再根据机械结构选择立足点。然而并没有保证所选择的立足点是否是机械腿所能达到的最优立足点，

本文针对四足机器人如何实现凹凸地形稳定行走的问题，从机械腿工作空间出发提出一种新的以稳定裕度为约束条件来选择有效立足点的方法，来实现选择最优立足点的目的。第一，建立四足机器人的运动学数学模型。第二，将机械腿的工作空间离散化，得到工作空间矩阵，然后选择最优步态规划区域，利用纵向稳定裕度从机械腿工作空间矩阵中计算有效立足点并选择最大步长，来规划足端轨迹。第三，进行数值分析及仿真实验，验证方法的正确性。

1 步态规划的数学模型

研究对象如图1所示：机器人由躯干和4条结构相同的机械腿组成。前腿包括肩胛骨、小腿和大腿三个部位；后腿由大腿、小腿和足部组成。前大腿(后小腿)结构为平行四边形结构。每条腿有3个主动自由度，1个联动自由度，整机共12个自由度。

图1 四足机器人简化模型

机器人腿部的几何参数如表1所示，总体尺寸：纵向髋距260 mm，横向髋距186 mm。

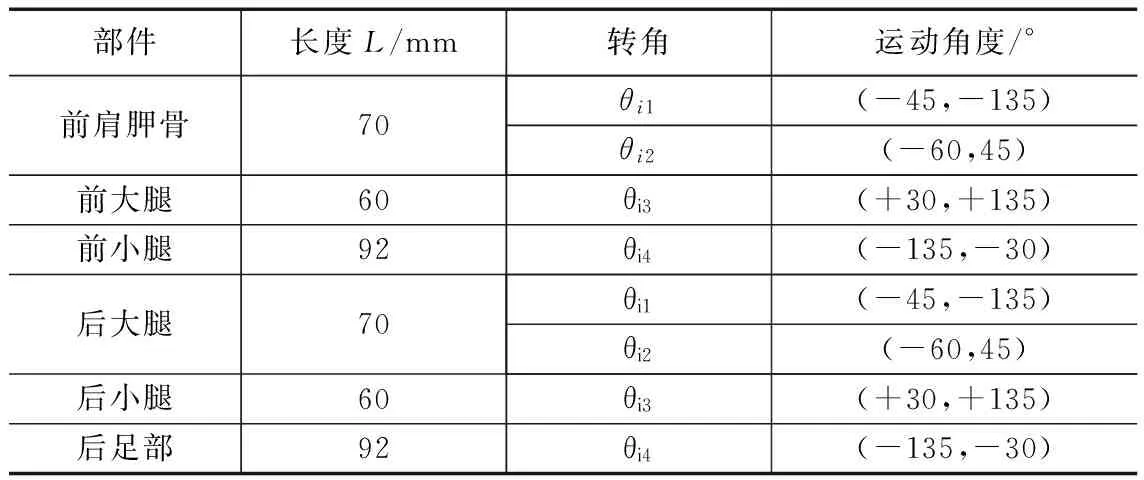
表1 四足机器人样机几何参数

1.1 运动学建模

1.1.1 正运动学模型

利用D-H法对四足机器人建立坐标系如图2所示:oc_xyz为质心坐标系，oi1_xyz为第i条腿的髋关节(肩关节)横向坐标系，oi2_xyz为第i条腿的髋关节(肩关节)纵向坐标系，oi3_xyz为第i条腿的膝关节(肘关节)坐标系，oi4_xyz为第i条腿的踝关节(腕关节)坐标系，关节转角变量分别为θi1、θi2、θi3、θi4，i=1,2,3,4分别为右前腿、左前腿、右后腿和左后腿。

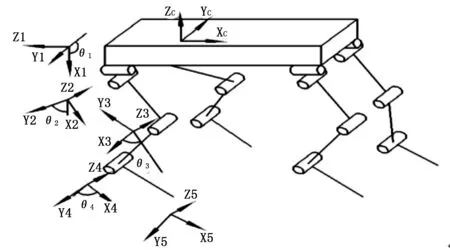
图2 四足机器人的坐标系

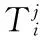
(1)

1.1.2 逆运动学求解

机械腿包含平行四边形结构，可以简化为两杆机构，利用几何法求解四足机器人的关节变量。对于后脚而言，如图3所示，质心坐标系oc_xyz为参考坐标系，后腿足端位置为P4(x4,y4,z4)，髋关节的位置为P1(m,n,zco)，大腿、小腿、后腿足部长度分别为l1,l2和l3。

图3 逆运动学求解

对于θi1而言，

(2)

对于θi2而言，在ΔABC和ΔABC′中，

(3)

(4)

(5)

对于θi3,θi4而言， 在ΔABC′中，

(6)

(7)

式(3)～(7)中，

结合(2)～(7)即可求解关节变量θi1,θi2,θi3,θi4的大小。机械前腿关节变量的计算亦如上所述。

1.2 立足点计算

四足机器人以右前腿、左后腿、左前腿、右后腿的迈腿顺序在复杂地形上行走时，凸台高度和凹坑深度由机器人躯干上的测距传感器感知。其运动需保持质心的水平投影处于支撑多边形内。前腿摆动过程中，其新立足点需保证对侧机械后腿能顺利抬起和落下。当后腿处于摆动相，其新立足点需保证同侧机械前腿能顺利抬起和落下。

单腿步距Ai：摆动腿i从抬起到落地过程中，机器人躯干相对地面的位移。

支撑腿运动裕度KMi：支撑腿i从支撑相某一位置到开始抬腿过程中，机器人躯干沿运动方向的位移。

LSMFi(LSMBi)：机械腿i抬起时，机器人的前(后)纵向稳定裕度。

LSMFi(LSMBi)：机械腿i落下时，机器人的前(后)纵向稳定裕度。

1.2.1 机械后腿立足点计算

后腿的立足点需保证同侧机械前腿能够顺利抬起和落下，即后腿i处于摆动相时，机器人的质心在支撑多边形内，且新立足点要留有足够的稳定裕度使同侧前腿j完成抬起和落足动作，可得以下约束条件：

(8)

其中：KMj为摆动后腿i的同侧前腿j的运动裕度；Ai为摆动后腿i的步距；LSM0为四足机器人运动过程中所需的最小纵向稳定裕度；min(Aj)为同侧前腿j的最小步距。

机械后腿的立足点计算如图4所示，P1(x1,y1,z1)，P2(x2,y2,z2)，P3(x3,y3,z3)为支撑腿立足点；P4(x4,y4,z4)为摆动腿抬起点，P4′(x4n,y4n,z4n)为新立足点。cog(xc0,yc0,zc0)为质心坐标。

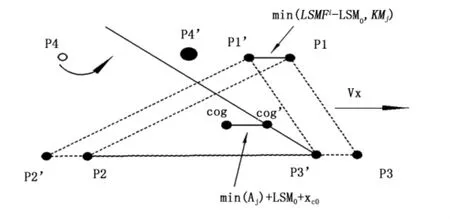
图4 后腿立足点计算示意图

(9)

式中，g(x4,z4,min(LSMFi-LSM0,KMj))为摆动后腿i足端的运动轨迹在min(LSMFi-LSM0,KMj)约束下，摆动后腿i前摆最大的距离，该值与机械腿运动轨迹函数及摆动后腿i的抬腿点P4(x4,y4,z4)有关。

1.2.2 机械前腿立足点计算

前腿的立足点需保证对侧的机械后腿能够顺利抬起和落足，即摆动前腿k处于摆动相时，机器人的质心在支撑多边形内，且新立足点要留有足够的稳定裕度使对侧后腿i完成抬起和落足动作，可得以下约束条件：

(10)

其中：KMi为摆动前腿k的对侧后腿i的运动裕度；LSM0为四足机器人运动过程中所需的最小纵向稳定裕度；Ak为摆动前腿k的步距；min(Ai)为对侧后腿i的最小步距。

根据以上条件，机械前腿的立足点计算如下图所示，P1(x1,y1,z1)，P2(x2,y2,z2)，P3(x3,y3,z3)为支撑腿立足点；P4(x4,y4,z4)为摆动腿抬起点，P4′(x4n,y4n,z4n)为新立足点。cog(xc0,yc0,zc0)为质心坐标。

图5 前腿的新立足点计算示意图

(11)

其中：g(x4,z4,min(LSMFk-LSM0,KMi))为摆动前腿k足端的运动轨迹在min(LSMFk-LSM0,KMi)约束下，摆动前腿k前摆最大的距离，该值与摆动腿运动轨迹函数及摆动前腿k的抬腿点P4(x4,y4,z4)有关。

1.3 摆动腿足端运动轨迹

机器人以恒定速度在复杂地形上运动，其运动轨迹分成抬腿轨迹Tp1，前摆轨迹Tp2及落脚轨迹Tp3三段。各足的立足点需要根据实际地形高度调整，最优立足点P4′(X4n,Y4n,Z4n)在质心坐标系下的高度Z4n由传感器来检测，而X4n和Y4n由2.2节计算可得。摆动腿从抬腿点P4(X4,Y4,Z4)到最优立足点过程中需要克服的凸台高度亦由传感器检测，以确定抬腿轨迹的最高点PTp1(X1,Y1,Z1)，前摆轨迹的最高点PTp2(X2,Y2,Z2)、落腿轨迹的最高点PTp3(X3,Y3,Z3)。X1与X4，X3与X4n间的关系根据所设计的具体曲线形状而定。机器腿摆动过程中，在没有发生碰撞的情况下，加速度连续，足端轨迹可利用3次样条曲线来确定，以抬腿轨迹的最高点PTp1和抬腿点P4、前摆轨迹的最高点PTp2、落腿轨迹的最高点PTp3和所计算的新立足点P4′为关键点，抬腿速度和落脚速度为边界条件，规划摆动腿的足端运动轨迹。方程如下：

(12)

(13)

其中:[t0,t1]为抬腿时间；[t1,t2]为前摆轨迹到前摆轨迹最高点时间；[t2,t3]为前摆轨迹从最高点到前摆轨迹结束点时间；[t3,t4]为落脚时间。

Vx，Vy，Vz为抬腿和落足速度在质心坐标系下X轴方向，Y轴方向和Z轴方向的速度分量。

2 四足机器人的步态规划

本文所提出的凹凸地形上的步态规划方法基于机械腿的工作空间，以纵向稳定裕度为约束条件，支撑腿的空间坐标和地形高度为已知条件，计算当前摆动腿的可行立足点并选择最优立足点以及规划摆动腿的足端运动轨迹。步态规划流程图如图6所示。

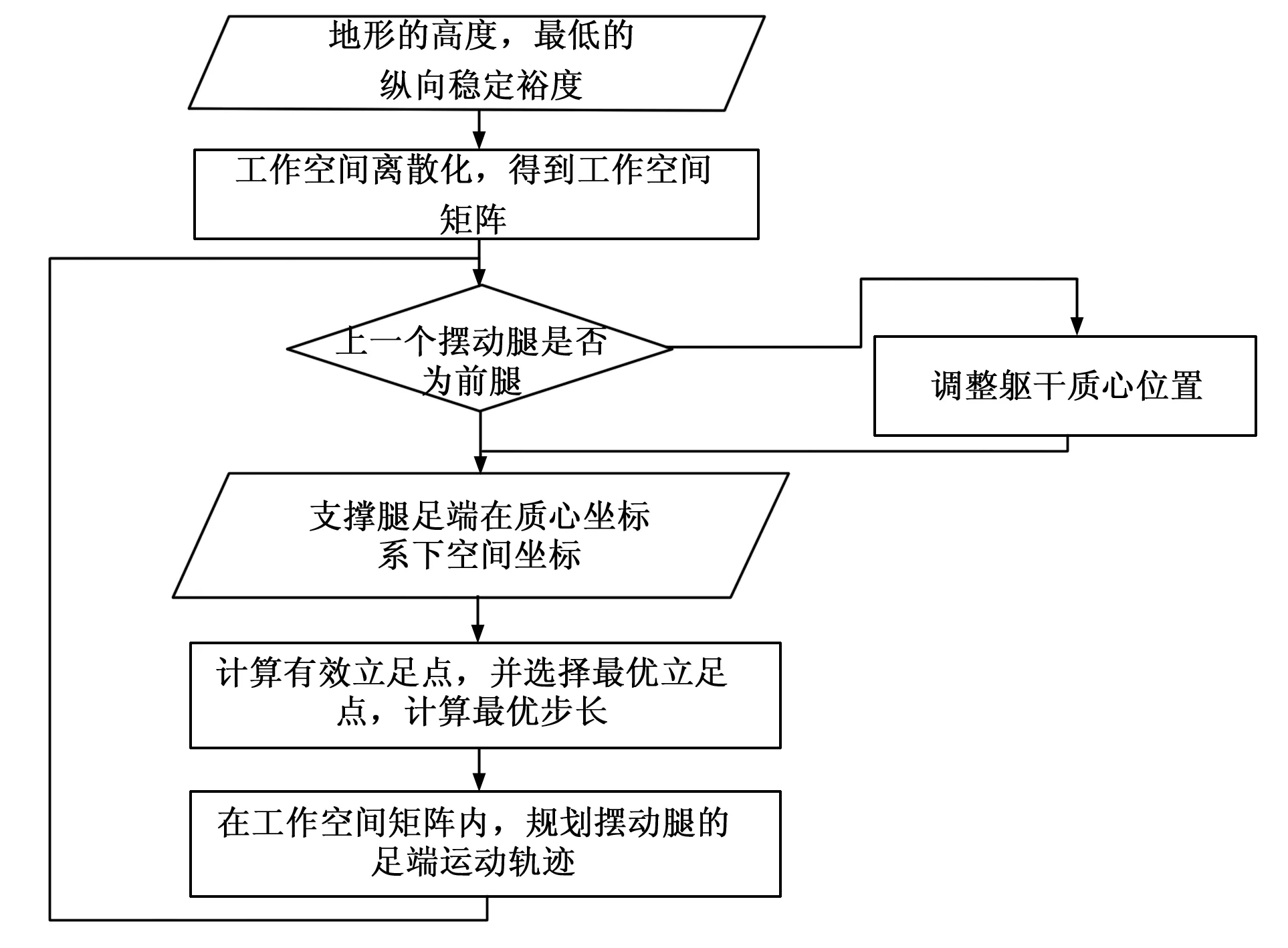
图6 步态规划流程图

2.1 单腿工作空间离散化

四足机器人在凹凸地形上行走时，所规划的立足点必须在机械腿的可达范围内。在机械腿的工作空间内进行步态规划是必须的。本文提出了一个步态规划的新思路：将机械腿工作空间离散化，得到一个能够反映机械腿工作空间形状特征的矩阵，并利用相关运算，将该矩阵融入到步态规划。

定义1:工作空间矩阵，指存在r×r维矩阵A0，若第i行，第j列元素A0(i,j)为机械腿可达，则该矩阵元素A0(i,j)为1，否则为0。

A0(i,j)为机械腿可达的判断依据如下：存在四个点B0(xmax-(i-1)b,zmax-(j-1)h)、B1(xmax-ib,zmax-(j-1)h)、B2(xmax-(i-1)b,zmax-jh)、B3(xmax-ib,zmax-jb)，若机械腿同时可达这四个点，则元素A0(i,j)为1，否则为0。其中xmax，xmin为质心坐标系下机械腿前进方向最大值和最小值；zmax，zmin为质心坐标系下竖直方向最大值和最小值。另外，b和h的计算如下：

(15)

式中，b为r×r工作空间矩阵下的单位步长；h为r×r工作空间矩阵下的单位抬腿高度。

2.2 基于工作空间矩阵的步态规划

基于工作空间矩阵的步态规划步骤如下：

(1)基于机械腿的几何参数获得工作空间矩阵A0；

(2)计算抬腿点P4在工作空间矩阵中的位置；根据测距传感器反馈的数据计算抬腿所需要行数和n；

(16)

式中，Hn为抬腿高度，抬腿点P4的高度与摆动腿工作空间内检测到的最大凸台高度在质心坐标系下的高度差。

(3) 根据抬腿所需要行数和n，抬腿点P4以及所设计摆动腿轨迹曲线中X1与X4之间的关系计算抬腿轨迹最高点PTp1在工作空间矩阵中的位置；对A0中行号小于PTp1所在行及列号大于PTp1所在列的区域中的元素清0，得到一个新矩阵A1；

(4)根据测距传感器反馈的数据计算落腿所需的最大行数和m；

(17)

式中，Hm为最大落腿高度，摆动腿工作空间内检测到的最大凸台高度与最大凹坑深度在质心坐标系下的高度差。

(5)对A1进行行扫描，选出连续列数和大于等于m的区域，而该区域外的元素清0，得到一个新矩阵A2，作为步态规划区域；

(6)根据1.2节内容，根据支撑腿的空间坐标计算出立足点范围，对A2进行筛选，将不满足1.2节计算条件的元素变成0；A2筛选后矩阵中左上角第一个值为1的元素为PTp3；最后进行PTp3和PTp1间列求和，得到最大前摆距离数mn，则摆动腿最大前摆距离如下：

B=mn×b

式中，B为摆动腿最大前摆距离。

(7)根据最大前摆距离，最大落腿高度，计算依据设计摆动腿轨迹曲线中X3与X4n之间的关系计算理论的新立足点P4′。根据抬腿点P4，抬腿轨迹最高点PTp1，落腿轨迹最高点Ptp3，理论的新立足点P4′规划摆动腿的运动轨迹；

需要注意的是，若在工作空间矩阵中，P4所在行的任意一列到上边界(矩阵元素为0)的行数和小于n，即PTp1所在行存在任意一列的元素为0，表明在摆动腿工作空间内存在无法越过的凸台；若A2为0矩阵，表明在摆动腿工作空间内存在无法可达的凹坑，此时需要其他躯干姿态调整方法。

3 数值实验分析

机器人样机模型的行走环境如图7所示，最大凸台高度为40 mm。

图7 机器人模型行走的地形

3.1 计算验证

3.1.1 工作空间矩阵在步态规划中的应用

根据表1得到四足机器人前腿的工作空间如图8所示。将该工作空间离散化后，所得到的工作空间矩阵A0如图9所示，与图8相比较，二者形状相似。

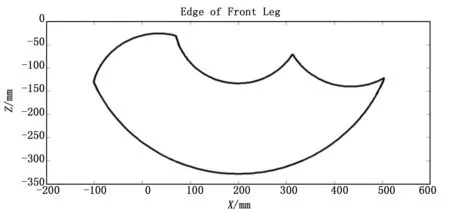
图8 单腿工作空间

图9 工作空间矩阵A0

按照2.2节步骤(2)～(5)，得到表征步态规划区域的A2矩阵如图10所示。矩阵元素为1的区域代表步态规划区域。

图10 步态规划区域A2

机器人在初始状态各支撑腿相对于质心参考坐标系的坐标系如下：右后腿P1(-141.08,-93,-176.25)，右前腿P2(159,-93,-176.25)，左后腿P3(-16.8,93,-176.25)，左前腿作为摆动腿且抬腿点P4(35.5,93,-176.25)。根据步骤(6),对A2进行筛选后，得到如下矩阵，通过求列数和，得到最大前摆距离为12b。

图11 有效立足点矩阵A3

已知抬腿点P4、抬腿轨迹的最高点PTp1、前摆轨迹的最高点PTp2、落足轨迹的最高点PTp3、新的落足点P4′以及机器人的运动速度，根据2.3节所规划的足端运动轨迹如图12所示。

图12 质心坐标系下足端运动轨迹

3.1.2 四足机器人步态图

机器人以20 mm/s行走于图7所示地形上，其纵向稳定裕度的最低要求为20 mm，所得到的立足点如下图所示。实心点为立足点，空心点为抬腿点。图中四足机器人的质心水平投影一直在支撑多边形内，即机器人的纵向稳定裕度始终大于0，因此机器人在运动过程中不会倾倒。这表明使用所提出的步态规划方法计算有效立足点时，能保证稳定性要求，这说明了所提出的步态规划方法在计算有效立足点方面是合适的。

图13 机器人步态图

3.2 仿真分析

3.1节得到的是机器人行走的立足点及摆动腿的运动轨迹。利用ADAMS软件进行仿真，通过分析四肢足端运动轨迹及躯干的姿态曲线和运动曲线，以验证所提出的步态规划方法是否能够达到目的。

四足机器人的ADAMS模型如图14所示。四足机器人运动过程中，四肢的运动轨迹如图15所示。Y轴为各足竖直方向的位移，X轴代表各足前进方向的位移。机器人摆动腿的足端运动轨迹形状与MATLAB所规划的运动轨迹相似，说明逆运动学求解的可靠性。机器人行走时，四肢的立足点不在同一高度上是由于所选择的立足点地形高度不一致所导致的。另外，机器人运动过程中左前脚迈步2次，左后脚迈步2次，右前脚迈步2次，右后脚迈步2次。

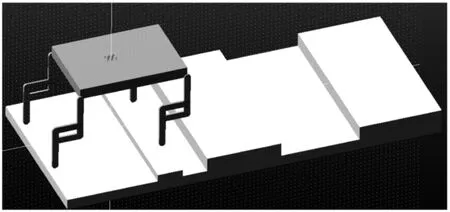
图14 四足机器人的ADAMS模型

躯干质心的位移曲线如图16所示，机器人在行走过程中，前进速度为20 mm/s，竖直方向位移波动幅度小于1 mm，而横向方向的位移递增幅度7 mm。竖直位移呈波动形状变化是由于腿部模型为连杆，存在一定的宽度。横向位移和竖直位移的大小相对于前进位移来说很小，可以认为机器人在运动过程中保持运动方向不变，且能够保持运动速度不变。

躯干的RPY角曲线如图17所示，四足机器人的俯仰角，偏转角及回转角的波动范围都在1°之内，由此可知四足机器人的姿态角变化很少，躯干的姿态基本保持不变。

由躯干的位移曲线及姿态角曲线可知，四足机器人在运动过程中，沿直线运动且速度不变。结合机械腿轨迹图，可知四足机器人运动过程中立足点不是在同一水平面，即机器人的立足点根据地形的高度变化而变化。综上所述，机器人在凹凸地形运动时，具有一定环境适应性。这说明所提出的步态规划方法可行。

4 结论

MATLAB所示步态图及ADAMS仿真结果表明：利用所提出的步态规划方法，机器人在凹凸地形上运动时，躯干姿态基本不变，运动速度恒定，且其立足点能够随地形高度变化而变化。所提出的步态规划方法直接在机械腿的工作空间内以稳定裕度为约束条件计算有效立足点，并能选择最大步长，从而使机器人具有更强的环境适应性。

5 结语

本文针对四足机器人如何实现凹凸地形稳定行走的问题，从新的角度(表征机械腿的工作空间的离散化矩阵)进行四足机器人的步态规划，使机器人能够保持稳定性的前提下基于机

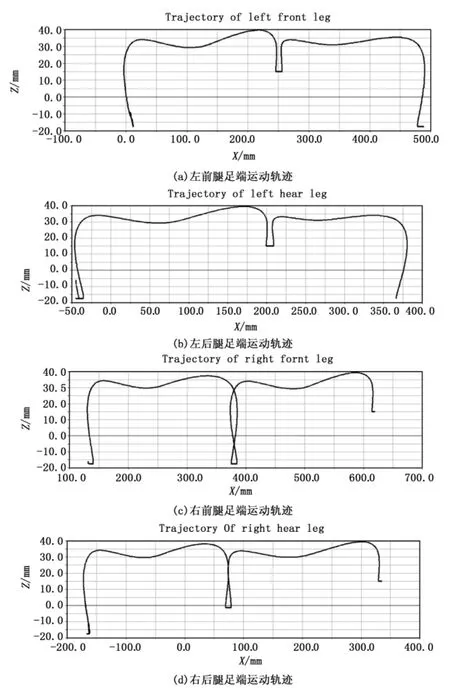
图15 四肢的运动轨迹

图16 躯干的位移曲线

图17 躯干的姿态角曲线

械腿的工作空间选择最大步长。然而，该方法还存在局限性，即最大步长的精度取决于矩阵的维数。另外，迈腿顺序为标准顺序，即前右脚，左后脚，左前脚，右后脚。后续工作可针对维数的选择及迈腿顺序对步态规划的影响展开深入的研究。

[1] Yibin L，Bin L，Jiuhong R，et al. Research of mammal bionic quadruped robots：a review[A]. IEEE 5th international conference on robotics，Automation and Mechatronics (RAM 2011)，September 17-19，2011[C].Qingdao，China. Piscataway，NJ，USA：IEEE，2011：166-171.

[2] Marc Raibert, Kevin Blankespoor.BigDog, the Rough-Terrain Quadruped Robot[A]. IFAC Proceedings Volumes (IFAC-PapersOnline)[C]. 2008,17(1):PART 1.

[3] Dimitris Pongas, Michael Mistry, Stefan Schaal. A robust quadruped walking gait for traversing rough terrain[A]. 2007 IEEE International Conference on Robotics and Automation[C]. Roma, Italy, April 2007,10-14.

[4] 鄂明成,刘 虎,张秀丽,等.一种粗糙地形下四足仿生机器人的柔顺步态[J].机器人,2014,36(5):584-591.

[5] Raibert M. Legged robots that balance[M]. Cambridge, USA:MIT Press, 1997: 58-80.

[6] Pratt J, Chew C M, Torres A, et al. Virtual model control: anintuitive approach for bipedal locomotion[J]. International Jour-nal of Robotics Research, 2001, 20(2): 129-143.

[7] Tran D T, Koo IM, Moon H, Et AL. Motion control of a quadruped robot in unknown rough terrains using 3dspring damper leg model[A].IEEE International Conferenceon Robotics and Automation[C]. Piscataway, USA: IEEE, 2012:4931-4936.

[8] Havoutis I, Semini C, Buchli J, et al. Quadrupedal trotting with active compliance[A].IEEE International Conference on Mechatronics[C]. Piscataway, USA: IEEE, 2013: 610-616.

[9] Kan Yoneda, S Hirose. Dynamic and static fusion gait of a quadruped walking vehicle on a winding path[A]. Proceedings of the 1992 IEEE International Conference on Robotics and Automation[C]. Nice,France, May,1992.

[10] S Hirose, Yasushi Fukuda, Kan Yoneda. Quadruped walking robots at tokyo institute of technology design, analysis and gait control methods[J]. IEEE Robotics and Automation Magazine, 2009,16(2):104-114.

[11] Mostafa Ajallooeian*, Sebastien Gay. Modular Control of Limit Cycle Locomotion over Unperceived Rough Terrrain[A].2013 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS)[C]. Tokyo, Japan. November,2013,3-7.

[12] Shaoping Bai K H. Low. A new free gait generation for quadrupeds based on primary/secondary gait[A]. International Conference on Robotice&Automation[C]. Detroit. Michigan.1999. pp.1371-1376.

[13] 王恒升.四足机器人躯干重心稳定的变步长行走研究[J].计算机仿真,2014,31(12):339-345.

[14] 刘冠初,熊静琪,乔 林.四足机器人自由步态规划建模与算法实现[J],西安交通大学学报,2015,49(6).

[15] 王新杰，李培根，陈学东，等.四足步行机器人动力学模型及脚力分配的研究[J].华中科技大学学报(自然科学版),2005,32(12):12-15.

Method of Gait Generating for Quadruped Robot Walking on Rough Terrain

Chen Yahui，Tan Yuegang，Li Zhang

(College of Mechanical and Electrical Engineering, Wuhan University of Technology，Wuhan 430070,China)

In order to realize the stable motion on rough terrain for quadruped robot, a new gait generating method based on stable margin was presented in this paper, which focus on implement of motion at a steady speed without fluctuation on body for the quadruped robot moving on the concave and convex terrain. Based on the structure of robot, kinematics equation and inverse kinematics equation of quadruped robot had been established, mapping the location of foot into the joint variables of each joint. A new concept-- working space matrix, had been proposed, which can reflect shape of leg’s work space and terrain parameters that robot should overcome. Taking longitudinal stability margin as the constraint condition，calculated effective footholds of the swinging leg in the working space matrix based on footholds of supporting legs in centroid coordinates. Then, selected the biggest step and planed trajectory of swinging leg in working space matrix, guaranteeing foot of swinging leg working in its workspace. It verified the proposed method by MATLAB and ADAMS. It was observed whether COG moved in the supporting polygon formed by the foothold in the MATLAB while the posture and displacement of body in the coordinated system were analyzed in the AdAMS. The simulation results showed that the robot's COG was always within the support polygon, while the robot's posture and movement speed were similar to the expectations. Therefore, the proposed method could guarantee the stability of the robot to walking on rough terrain and put forward basis theory for the stability movement of the quadruped robot

quadruped robot; walking tread; working space matrix; motion planning

2016-01-22；

2016-03-07。

中央高校基本科研业务费专项基金(155204001)。

陈雅辉(1990-)，男，广东珠海人，硕士，主要从事机器人技术与应用方向的研究。

谭跃刚(1959-)，男，四川重庆人，教授，博士，主要从事机器人技术方向的研究。

1671-4598(2016)07-0262-06

10.16526/j.cnki.11-4762/tp.2016.07.071

TN713

A