无人水面艇模型辨识及其航向非线性控制的研究

江立军，慕东东，范云生，王国峰，赵永生

(1.海军驻大连地区军代表室，辽宁 大连 116026；2.大连海事大学 信息科学技术学院，辽宁 大连 116026)

无人水面艇模型辨识及其航向非线性控制的研究

江立军1，2，慕东东2，范云生2，王国峰2，赵永生2

(1.海军驻大连地区军代表室，辽宁 大连 116026；2.大连海事大学 信息科学技术学院，辽宁 大连 116026)

无人水面艇是一种智能化海洋装备平台，有航速快、机动性强、自动化程度高等特点，可以执行各种危险以及不适合人员参与的任务;航向控制不仅关乎到航行的安全性与经济性，更是实现其无人行驶的基础;为了实现航向的自动控制，首先进行无人艇模型辨识，模型是控制的基础，控制效果的好坏不仅与控制策略有关，更与模型的精度有关;为了提高模型精度，采集Z型和回转实验以数据，通过递推最小二乘对无人艇的数学模型进行辨识;然后将模型的仿真实验与实船数据进行对比，验证了模型的正确性和合理性;基于Backstepping方法设计非线性航向控制器，借助Lyapunov 函数证明了闭环系统的稳定性;仿真结果表明系统的实际航向能实时跟踪设定航向，控制器具有良好的动静态特性和鲁棒性。

无人艇；航向；递推最小二乘；模型辨识；Backstepping

0 引言

无人水面艇(unmanned surface vehicle, USV)拥有体积小、机动性能强、航速快等特点，它主要用来执行危险及不适合人工操作的任务，己成为了国内外智能化海洋装备的研究热点。USV的自主航行一直是船舶控制领域的研究热点与重点[1]。其中航向控制更是运动控制的重要研究课题之一，因为它不仅关系到航行的经济性与安全性，更是自动避碰、航迹跟踪、轨迹跟踪以及镇定问题等的基础。要想设计一款性能良好的控制器，除了要依赖各种“高级的”控制算法，还取决于被控对象的模型精度，所以如何获取USV的操纵运动模型是设计运动控制器的基础，也是研究USV自主控制技术的核心内容之一。通常利用系统辨识的方法来确定模型参数是最简单有效也相对精确的方法，在现有文献中，辨识的方法主要有最小二乘法[2]、扩展Kalman滤波法[3]、模型参考自适应方法[4]、极大似然估计法[5]、回归预报误差法[6]、岭回归分析法[7]、神经网络法[8]、频域谱分析法[9]、支持向量机法[10]和遗传算法[11]等。其中，最小二乘法则是系统辨识中最常用的方法[12-13]，即可应用于线性系统也可应用于非线性系统；可应用于离线估计，也可应用于在线估计，且具有算法简单、易于理解、计算量少等特点。

随着科学技术以及自动控制理论的不断发展，时至今日，船舶自动舵先后经历了机械式自动舵、PID自动舵、自适应性自动舵和智能舵[14]。国内外已对航向控制做了较深入的研究，可以查询到大量的文献以及各种控制方法。文献[15]采用频率成型滑模算法对USV模型参数进行辨识，然后运用滑模控制器与滑模观测器设计了一套控制系统，在模拟仿真中取得了预期的控制效果。文献[16]针对无人艇非线性、多变量等特征将SVR引入USV的航向控制，提出了自适应SVR控制方法。该方法以输入输出反馈线性化理论为基础，辨识出直接自适应逆控制系统模型，最后在模拟仿真中证明了该控制方案具有良好的控制效果与动态响应特性。Alfaro-Cid等[17]采用遗传算法优化滑模控制器中的参数，改善船舶的航向运动控制。张显库教授[18]将简化的逆推算法与闭环增益成型算法结合，提出了一种设计算法简单、物理意义明确的非线性鲁棒控制器。通过模拟仿真表明，该控制器能够使船舶无超调无静差的跟踪规定航向，控制效果好、收敛速度快、具有一定的鲁棒性。但目前而言，国内外的专家学者在智能舵上的研究尚处于理论研究与模拟仿真阶段，且PID算法简单易于工程实现，所以应用最为广泛的仍是PID自动舵[19]。

本文采用Norrbin模型来描述USV，然后根据大连海事大学“蓝信”号[20]实船数据来辨识模型参数，并在后续的实验中验证模型的正确性与精确度。在第三章基于backstepping方法设计了非线性航向控制器，并在第四章进行模拟仿真以验证航向控制器的可行性与正确性。

1 USV模型及其辨识

1.1 Norrbin Model

在设计航向控制器时，船舶平面运动数学模型通常采用Nomoto模型，但是Nomoto是在低频操舵以及小舵角的情况下推导出来的，而USV有着较快的航速往往需要高频操舵，所以Nomoto不适用于USV。在考虑模型的非线性以及复杂程度的基础上，本文采用Norrbin模型来设计航向控制器[21]。

(1)

其中:ψ为航向角，δ为输入舵角，n0，n1,n2,n3为Norrbin系数，K为增益，T为时间常数。当USV具有对称结构时，n0=n2≈0当USV具有具有直行特性时n1=1，否则n1=-1。 所以公式(1)可以简化(2)。

(2)

K,T和n3是需要被辨识的系数。

设x1=ψ和x2=r，则公式(2)可以转化为状态空间方程(3)。

(3)

1.2 数据采集

在宽阔海域的条件下，USV进行回转实验。USV船速保持在9 kn左右，分别以5°、8°、10°、15°、20°、25°、30°、35°舵角进行回转实验，采样时间为0.5 s。由于记录数据较多，本文中只列出5°时的部分数据，如表1所示。

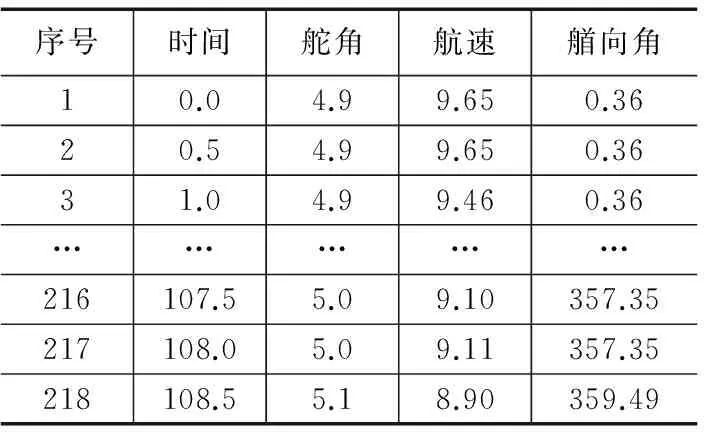
表1 5°回转实验数据

基于多组回转实验数据，分别求出相应舵角下的艏摇角速度，如表2所示。

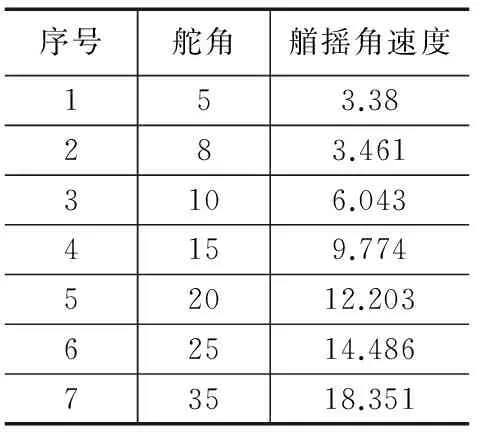
表2 舵角与相应艏摇角速度

在同样的海况与航速下，USV进行15°/15°Z型操纵实验。由于各种干扰的存在以及机械特性，在整个实验过程中，允许目标舵角与实际舵角存在一定的误差。部分Z型数据如表3所示。

表3 15/15 Z型试验数据

1.3 参数辨识

(4)

USV数学模型的系统辨识过程如图1所示。

图1 辨识原理图

图2 Z型辨识参数收敛曲线

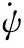
(5)

其中:K为已知，n3为待辨识参数。经拟合可知n3=0.001。拟合曲线如图3所示。

图3 舵角与艏摇角速度拟合曲线

为了验证辨识模型的正确性，将模拟回转实验与实船回转实验进行比较。比较结果如图4所示。

图4 比较结果

从图4中可以看出，无人艇的仿真稳定回转半径为85.762 1 m而实船稳定回转半径为84.971 6 m。通过比较可知，船舶模型在实际可信范围内。

2 控制器设计

Backstepping是针对严格反馈系统，通过变量代换和构造李雅普诺夫函数，使系统在平衡点满足一致渐进稳定[23]。 (3) 就是一个典型的严格反馈系统。

首先，定义一个新的航向误差。

(6)

Ψd是目标航向。对(6)求时间的导数得:

(7)

即:

(8)

定义x2为虚拟控制函数和另一个状态变量z2。

(9)

α(z1)是可以使x1→0的镇定方程。将(7)和(9)带入(10)建立系统的第一个李雅普诺夫函数。

(10)

(11)

对(11)求时间的导数，可得:

(12)

即:

(13)

取:

(14)

其中:k1>0是控制参数。将(14)带入(13)可得:

(15)

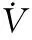
第二，通过一系列步骤使z2稳定。对(9)进行求导得:

(16)

进一步化简可得:

(17)

建立系统的第二个李雅普诺夫函数:

(18)

定义:

(19)

对(18)求导得:

(20)

将(20)化简得:

(21)

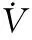
(22)

其中:k2是正的参数。将(22)带入(21)得:

(23)

而且(∀z1≠0,∀z2≠0)。

通过分析李雅普诺夫函数可知，当控制率取(22)时，z1和z2都是稳定的，即整个系统是稳定的。对(14)求导得:

(24)

通过化简得:

(25)

将(25)带入(22):

(26)

3 模拟仿真

3.1 环境干扰

USV在航行过程中，受到风、浪、流的干扰。流通常只对位置产生，所以本文只考虑风和浪的干扰。根据文献[21]和[24],fA-风干扰和fw-浪干扰分别可表示为：

(27)

(28)

式中,各项参数和变量的含义请参考文献[24]和[25]。风和浪的干扰是一个随机的过程，它们对USV的影响可以通过对其频谱密度的描述进行概括。为简单起见，这里采用一个二阶海浪模型来模拟实际的风浪干扰。

(29)

其中:w(s)为功率谱为0.1、均值为零的白噪声，L(s)为二阶海浪传递函数。

(30)

其中:σw为描述波浪强度的常数，w0是海浪频率，ξ为阻尼系数。当海况风力为5级时，参考文献[26]，L(s)为:

(31)

干扰曲线如图5所示。

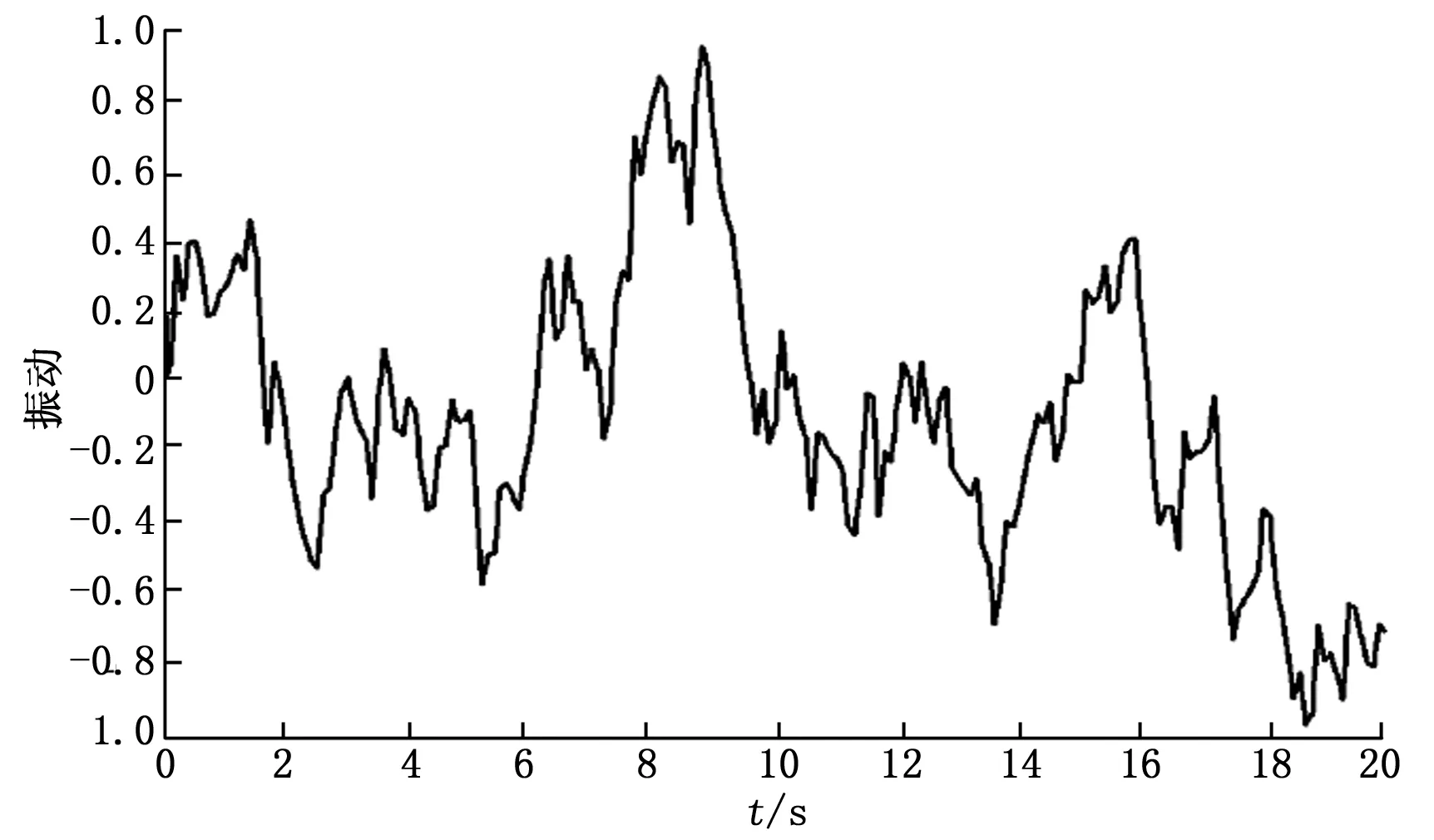
图5 干扰曲线

3.2 仿真

为了证明航向控制器的正确性与鲁棒性，在相同的干扰下，将PID航向控制器与backstepping航向控制器进行比较。PID的控制参数P=40、I=0、D=0.1。Backstepping的控制参数K1=35、K2=15。航向比较结果如图6所示，相应的舵角变化曲线如图7所示。

图6 航向曲线

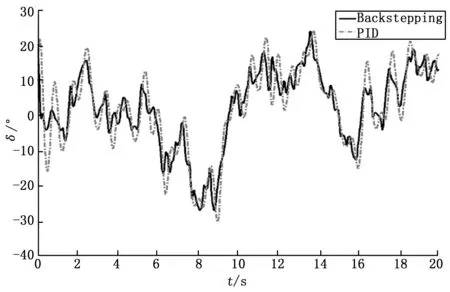
图7 舵角曲线

从图6可以看出，以正弦曲线为目标值，PID航向控制器和backstepping非线性航向控制器都可以实时跟踪目标值，但非线性控制器的控制效果优于PID。从图7也可以看出，非线性控制器的舵角波动幅度小于PID。由此证明了本文所设计的backstepping非线性航行控制器的可行性与鲁棒性。

4 结语

针对USV自动航向控制问题，在考虑模型的非线性和复杂度的基础上，选取Norrbin模型来描述USV的运动响应。本文首先通过Z型和回转实验采集实船数据，然后使用递推最小二乘对USV的数学模型加以辨识。为了验证辨识结果的正确性，通过仿真实验表明模拟回转半径与实际半径相差0.790 5 m,结果在可信范围内，可以基于此模型设计控制器。然后依据backstepping和李雅普诺夫函数设计了航向控制器，仿真实验表明在相同的风浪干扰下，本文所设计的非线性航向控制器控制效果优于与PID控制，证明了此控制器的可行性与鲁棒性。

[1] Gao S, Zhu Q, Li L. Fuzzy NN Control of High-speed Unmanned Ship [J]. Journal of System Simulation, 2007, 4: 018.

[2] 张洪东, 李 宏, 郑 勇. 基于递推最小二乘法的永磁同步电动机参数辨识[J]. 微特电机, 2011, (11):14-16.

[3] Abkowitz M A. Measurement of hydrodynamic characteristic from ship maneuvering trials by system identification[J]. Transactions of Society of Naval Architects and Marine Engineers, 1980, (88):283-318.

[4] Van Amerongen J. Adaptive steering of ships - a model reference approach[J]. Automatica, 1984, 20(1):3-14.

[5] 安其昌, 张景旭, 孙敬伟. 基于极大似然估计的TMT三镜轴系装调[J]. 红外与激光工程, 2013, (11):3002-3007.

[6] Zhou W W, Blanke M. Identification of a class of nonlinear state-space models using RPE techniques[J]. IEEE Transaction on Automatic Control, 1989, 34(3):312-316.

[7] 罗伟林, 邹早建. 基于岭回归方法的船舶操纵运动建模[J]. 船海工程, 2009(6):17-19.

[8] Moreira L， Guedes Soares C. Dynamic model of manoeuvrability using recursive neural networks[J]. Ocean Engineering, 2003, 30(13): 1669-1697.

[9] Bhattacharyya S K, Haddara M R. Parameter identification for nonlinear ship manoeuvring[J]. Journal of Ship Research, 2006, 50(3):197-207.

[10] Luo W l, Zou Z j. Parametric identification of ship manoeuvring models by using Support Vector Machines, Journal of Ship Research[J]. 2009, 53(1):19-30.

[11] 王立军, 张显库. 响应型船舶运动模型的建模与遗传算法辨识[J]. 中国航海, 2013(2):33-37.

[12] 李 涌. 基于最小二乘法的汽轮机电液调节系统参数辨识[J]. 电力与能源, 2013, 34(1):27-29.

[13] Yunsheng F, Xiaojie S, Guofeng W, et al. On fuzzy self-adaptive PID control for USV course[C].Control Conference (CCC), 2015 34th Chinese. IEEE, 2015: 8472-8478.

[14] Velagic J, Vukic Z, Omerdic E. Adaptive fuzzy ship autopilot for track-keeping[J]. Control engineering practice, 2003, 11(4): 433-443.

[15] Bao X, Nonami K, Yu Z. Combined yaw and roll control of an autonomous boat[A].Robotics and Automation, 2009. ICRA'09. IEEE International Conference on. IEEE[C]. 2009: 188-193.

[16] 孙巧梅, 任 光. 自适应逆控方法的无人艇航向控制[J]. 中国航海, 2013, 35(4): 17-21.

[17] Alfaro-Cid E, McGookin E W, Murray-Smith D J, et al. Genetic algorithms optimisation of decoupled Sliding Mode controllers: simulated and real results[J]. Control Engineering Practice, 2005, 13(6): 739-748.

[18] 张显库. 船舶航向保持的非线性逆推鲁棒控制算法[J]. 大连海事大学学报: 自然科学版, 2007, 33(2): 80-83.

[19] Roberts G N, Sutton R, Zirilli A, et al. Intelligent ship autopilots-A historical perspective[J]. Mechatronics, 2003, 13(10): 1091-1103.

[20] Yunsheng F, Zenglu G, Yongsheng Z, et al. Design of information network and control system for USV[C].Society of Instrument and Control Engineers of Japan (SICE), 2015 54th Annual Conference of the. IEEE, 2015: 1126-1131.

[21] 贾欣乐, 杨盐生. 船舶运动数学模型: 机理建模与辩识建模[M]. 大连:大连海事大学出版社, 1999.

[22] 刘金琨. 先进 PID 控制 MATLAB 仿真[M]. 北京：电子工业出版社, 2004.

[23] Witkowska A, Smierzchalski R. Nonlinear backstepping ship course controller[J]. International journal of automation and computing, 2009, 6(3): 277-284.

[24] 杨盐生, 郭子瑞. 船舶在非定常风中的舵力保向[J]. 大连海运学院学报, 1993, 19(2): 145-152.

[25] Yang Y. Study on ship manoeuvring mathematical model in ship handling simulator[J]. 1996.

[26] 杨承恩, 贾欣乐, 毕英君. 船舶舵阻横摇及其鲁棒控制[M]. 大连：大连海事大学出版社, 2001.

Study on USV Model Identification and Nonlinear Course Control

Jiang Lijun1,2, Mu Dongdong2, Fan Yunsheng2, Wang Guofeng2, Zhao Yongsheng2

(1.Office of Navy Military Representatives in Dalian, Dalian 116002, China;2.College of Information Science and Technology, Dalian Maritime University, Dalian 116026, China)

Unmanned Surface Vehicle is an intelligent platform for marine equipment, having the characteristics of fast speed, high mobility and high degree of automation. It can perform a variety of dangerous and not suitable for personnel missions. Course control is not only essential to the security and economy of the navigation, but also the basis for unmanned driving. In order to achieve automatic control of course, unmanned boat model is identified firstly. Model is the basis of control, and the control effect good or bad is not only related with the control strategy and more about the accuracy of the model. To improve the accuracy of the model, collecting the data of z test and rotation test in the primary sea condition, the model is identified by Recursive Least Squares. To further verify the correctness of the model, simulation tests are compared with the actual data. Nonlinear course controller is designed by backstepping method and the stability of the system is proved by Lyapunov function. Simulation results show that the actual course of system can track the target course quickly and The controller has good dynamic and static characteristics and robustness.

USV；course；RLS；model Identification；Backstepping

2016-05-23；

2016-05-31。

辽宁省自然科学基金(2015020022); 中央高校基本科研业务费专项基金(3132014321,3132016022)。

江立军(1960-)，男，教授，高级工程师；从事舰船系统设计与监造的研究。

范云生(1981-)，男，讲师，博士，主要从事船舶智能控制理论、无人系统测控技术等方向的研究。

1671-4598(2016)07-0133-04

10.16526/j.cnki.11-4762/tp.2016.07.035

TP273 文献标识码：A