精密离心机动态半径的定位测量技术研究

张 荣,王 珏,周继昆,张 毅,郑 敏

(中国工程物理研究院总体工程研究所，四川 绵阳 621900)

精密离心机动态半径的定位测量技术研究

张 荣,王 珏,周继昆,张 毅,郑 敏

(中国工程物理研究院总体工程研究所，四川 绵阳 621900)

精密离心机动态半径是影响精密离心机输出加速度精度的主要参数；对于高精度精密离心机的研制，必须对动态半径进行精密测量，并将测量结果作为补偿分量加入到精密离心机输出加速度修正数学模型中，以获得精确的加速度信号，同时为精密离心机输出加速度的精确评定奠定基础；文章介绍了精密离心机动态半径的外基准定位测试技术，包括多个定位平台的定位测试技术论证、测试系统配置等；该方法已应用于某高精度精密离心机动态半径测量中，实测结果表明，采用这种测量方法，动态半径的测量标准差为σ=0.21 μm，其测量精度满足高精度精密离心机研制的技术指标要求。

精密离心机；动态半径；定位测量；外基准

0 引言

精密离心机动态半径是精密离心机的关键参数，在10—6以上量级精密离心机研制中，需精确测量离心机动态半径，并将动态半径加入精密离心机输出加速度数学模型[1]中，以得到高精度的加速度信号输出。在10—6量级精密离心机研制中，精密离心机动态半径ΔR测量标准不确定度达0.3～0.6 μm，高精度测试指标对测试技术要求很高，本文在调研国内外动态半径测试技术基础上，提出利用外基准定位测试技术，采用电容测微仪和变采样率测试法，实现高精度精密离心机上四个定位平台的动态半径精确测量，达到了项目要求的半径测试精度技术指标。本文详细介绍动态半径定位测试方案，包括定位测试技术理论论证、测试系统配置与试验测试验证等内容。

1 动态半径ΔR的测试方案

调研表明，精密离心机动态半径ΔR尚无统一测量方法，测量基准分内基准与外基准两类，测量方式又分接触式和非接触式两类。内基准测试是将动态半径测试系统安装在离心机转盘上随离心机同步转动，测试系统非常复杂；外基准测试是将动态半径测试系统安装在离心机机体外，测试更容施行。内基准测试假定基准为离心机主轴的理想旋转中心，不考虑主轴回转误差引起转盘半径的变化，而外基准是以传感器安装支架为基准，测试结果包含主轴径向回转误差e，对于10-6量级精密离心机，当e远小于ΔR时，可不考虑e对动态半径的影响，否则需将e补偿到动态半径中，本文介绍的离心机主轴回转误差为实测为0.2 μm，故不考虑主轴径向回转误差对动态半径测试带来的影响。表1[2]是国内外精密离心机动态半径测试主要方法，由表1可知，美国在10-6量级的精密离心机动态半径测试时主要采用电容测微仪与外基准测试法。参考美国精密离心机动态半径测试方法，结合本项目研制的盘式精密离心机，在项目中采用外基准+电容测微仪非接触方式测量精密离心机动态半径ΔR。外基准选择为大地，动态半径ΔR相对于大地坐标系。

表1 各型精密离心机动态半径测试方法表

建立外基准利用电容测微仪直接对准精密离心机上的定位平台边缘测试其径向半径变化时，受机械加工能力限制，平台边缘无法做到精密加工，其形状误差通常为道级，这使得动态半径测试结果中包含平台边缘形状误差ΔS,如图1所示。

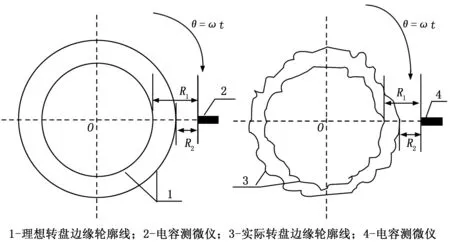
图1 理想转盘与实际转盘的动态半径测试示意图

对于理想定位平台不考虑其边缘形状误差，采用电容测微仪直接测量平台的径向变化量，电容测微仪安装好后，在离心机静止或在ωg下转动时，认为定位平台不存在半径变化，对电容测微仪的初值作多次采集并平均得R1，再在稳定的ω下采集多周数据并平均得到R2，则动态半径ΔR可由式(1)确定。

(1)

若考虑平台边缘形状误差ΔS，对平台全周采集N点，每点对应的形状误差为ΔSi。

(2)

(i=1,2,…N)，若满足式(2)，则测试数据多周平均处理后测量结果中包含的平台边缘形状误差对测量结果影响可忽略，但实际上平台边缘形状误差未知，本项目中转盘半径为1 m，在机械加工时精密控制其上四个定位平台边缘形状误差是困难的，此形状误差为道级，对于10-6量级的精密测量，应考虑平台形状误差对动态半径测量的影响，需采用创新技术途径消除形状误差对测量结果的影响，定位测量法就是在这种需求下提出的。因此，在本项目中，采用定位测试法测量精密离心机定位平台的动态半径ΔR。

1.1 动态半径测试总体方案

该精密离心机上设计有四个加速度计测试安装工位(定位平台)，为测量精密离心机运行时因离心力和温度变化等因素引起的加速度计输入轴方向的动态伸长量Ra，在定位平台外边缘安装单只电容测微仪进行定位测试，电容测微仪通过固接在地基上的安装支架固定，测试如图2所示。

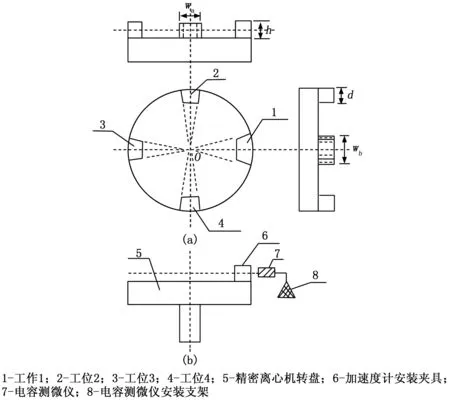
图2 定位平台径向伸长量Ra测试方案

图2中，精密离心机上设计的四个定位平台尺寸不全相同，其中工位2、工位3、工位4定位平台尺寸完全一致，工位1定位平台沿转盘圆周方向的尺寸wb大于其他3个工位定位平台在圆周方向的尺寸wa，这样设计有利于定位测量中判断Ra的一周测试数据中哪部分数据对应哪只待标检的加速度计输入轴向的半径变化量。采用单只电容测微仪进行测试是为了减小Ra的测量不确定度，若在转盘的180°方向再对称安装一只电容测微仪测量Ra，则Ra的测量不确定度为两只电容测微仪的测量不确定度合成，增大了动态半径ΔR的测量不确定度，不利于总体指标的实现。

1.2 动态半径定位测量理论分析

精密离心机转动时对电容测微仪信号进行采集，当四个工位定位平台分别对准电容测微仪时，测微仪进入有效测试区，当四个定位平台分别离开电容测微仪时，电容测微仪超量程进入饱和工作区并输出5 V固定电压信号，根据5 V固定电压信号结合各定位平台物理长度可定位出那段半径有效测试数据对应那个定位平台。设Pa为电容测微仪测得的原始数据，其中四个工位定位平台的径向测量原始数据分别设为Pa1、Pa2、Pa3、Pa4，离心机转动一周的理论测试波形如图3所示。

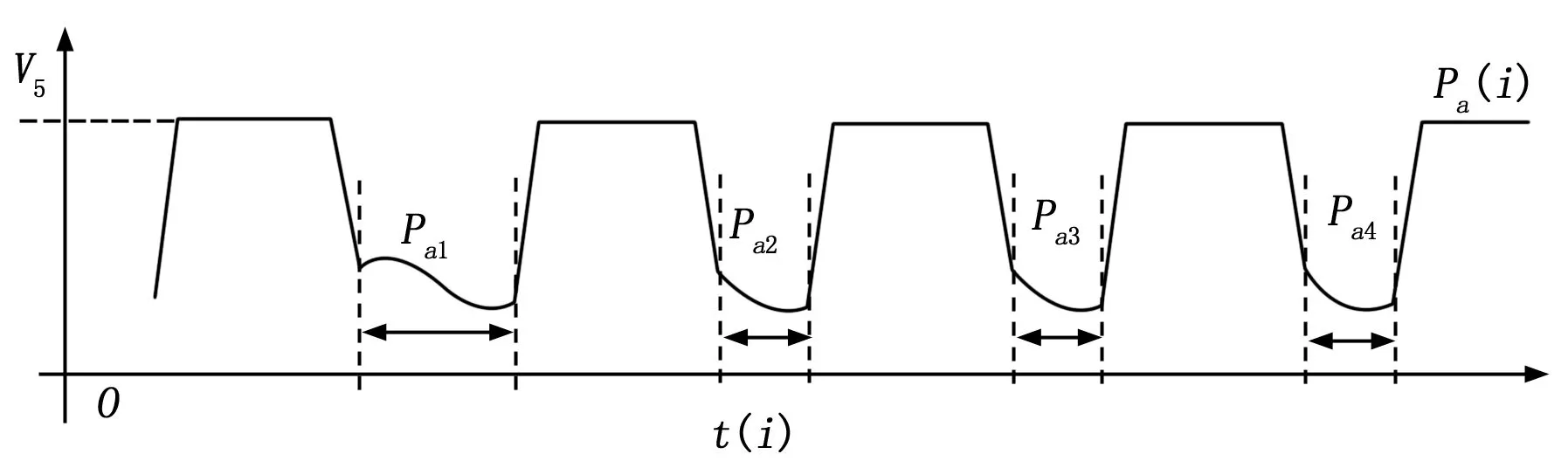
图3 四工位定位平台径向伸长定位测量理论波形

图3中，因工位1定位平台外缘圆周长度大于其他3个定位平台外圆周长，理论上工位1定位平台的有效测试数据长度应大于其他3个工位定位平台的有效测试数据长度，通过设定阈值，利用软件可搜索出Pa1、Pa2、Pa3、Pa4区域的数据分别作为稳定转速ω下各定位平台的径向尺寸测试原始数据。在ω1、ω2两种不同的稳定转速下，可测得两组原始数据，两组数据相减即得各定位平台在两种转速下的相对径向伸长量Ra1、Ra2、Ra3、Ra4。为验证电容测微仪是否输出定位信号，在10-5级精密离心机上开展挖槽定位测量验证试验，测得电容测微仪输出波形如图4所示。

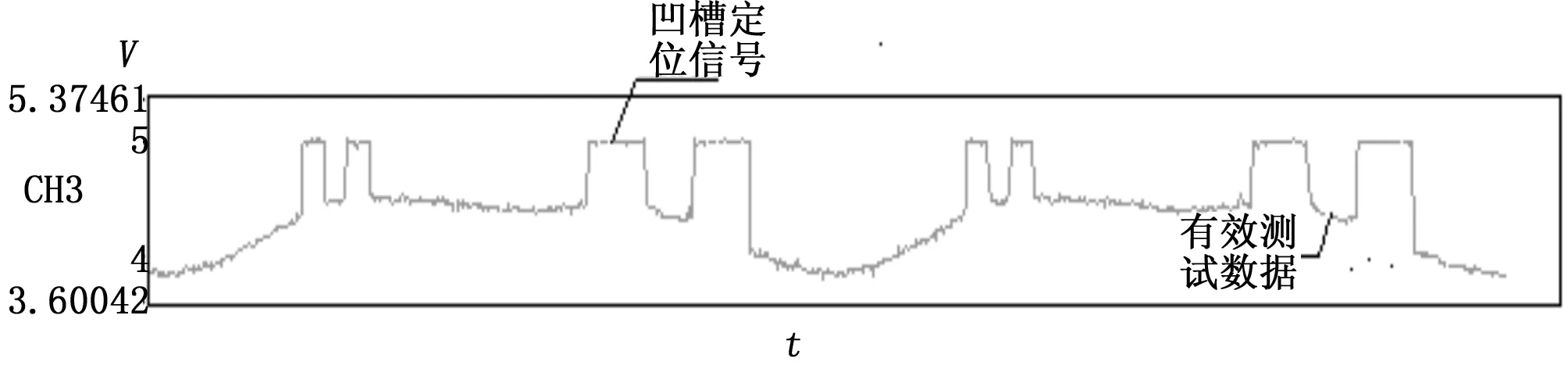
图4 利用电容测微仪和凹槽开展定位测量验证实测信号图

图4中的平坦信号代表凹槽对准电容测微仪时电容测微仪超量程工作输出幅值为5 V的定位信号，凹槽间的部分为有效测试数据。从图4可知，电容测微仪从超量程转入有效测试区信号的边沿陡峭，凹槽定位信号明确，定位测试方案可行。

1.3 消除定位平台外缘形状误差理论分析

在原始测量值Pai(i=1,2...N)中既包含定位平台径向伸长量Ra，也包括定位平台外缘加工形状误差ΔS，为消除定位平台外缘形状误差ΔS对测量结果影响，采用测点位置对齐测试法，测点位置对齐测试法认为在某稳定的转速ω下定位平台外缘形状不变，将转盘全周等角分为N个测点区域，在任何稳定转速ω下，对转盘全周均只采集N个测点，只要高低g值下同一测点Ti相对电容测微仪的测试区域是对齐的，则可通过两次数据采集，对高低g值下同一测点Ti的两次测量信号相减，分离掉测点Ti处的形状误差。前期技术方案研究表明，当精密离心机在高g值下的转速ω稳定度达10-7和1g下转速稳定度达10-4时，利用精密离心机的Z相脉冲作为采集触发信号，高低g值下同一测点因角速度波动引起测点在圆周方向上的偏移量为0.76 μm[3]，此偏移量不会引起电容测微仪的显著变化，因此高低g值下同一测点的形状误差在总测量值中的分量是相同的，故采用高、低g值下的测试信号相减即可实现消除定位平台形状误差，又可实现定位平台径向伸长量的测量，测试系统具体设计时需根据上述理论确定采样频率fs、采样点数N、触发设计。

1.4 定位平台径向伸长量Ra的测量总体设计方案

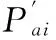
图5 Ng相对1 g下的定位平台径向伸长量测量示意图

1.5 定位平台圆弧长度wa、wb设计

设精密离心机的最大转速为ωmax，以弧度/秒为单位，精密离心机名义半径为R，电容测微仪的频响上限为fc，为使电容测微仪稳定测量定位平台区域内的信号，则定位平台在圆周方向的长度对应的最小时间tmin应大于或等于1/fc，对于最大转速ωmax，则有：

(3)

(4)

对于本台精密离心机，其名义半径R=1 m，设电容测微仪的频响上限为8 kHz，离心机输出加速度为1 g～100 g，则为在100 g下检测到定位区域，长度w至少为：

(5)

由于定位平台的径向伸长量应为多点数据的平均，对于全周采集N个点，设工位1定位平台的有效测试数据点数N1=30,为确保分辨工位1与其他工位的测试数据，设其他工位定位平台的有效测试数据点数N2=N3=N4=20，这样可保证10个有效数据宽度的分辨率，则工位1定位平台外圆弧长wa=30×3.91=11.7 cm，其他工位定位平台外圆弧长wb=20×3.91=7.82 cm，工程设计时可根据精密离心机半径R作对应的调整。

2 测试系统设计

2.1 数据采集与传输系统设计

数据采集与传输系统组成如图6所示。

图6 动态半径测量信号采集与传输示意图

图6中，电容测微仪作为获取信号始端位于精密离心机主机所在工号内，而信号二级放大器DT6530[4]以及数据采集卡PXI-4462[5]位于测控间，两者之间距离为20 m，为提高动态半径测量精度，在电容测微仪附近增加信号预放大器CP6001[4]，增加信号传输距离，预放大的信号通过二级放大器DT6530补偿放大后，输出0～10 V(代表0～250 μm)信号，送入高精度数据采集卡PXI-4462进行采集。

为对精密离心机的各定位平台进行定位采集，采用精密离心机主轴上的光栅编码器Z相脉冲信号作为采集触发信号，当精密离心机处于各高度稳定转速时，各定位平台在高低转速下的信号采样区域始终保持相同，可确保高精度定位测试的技术实现。其中，为了高转速下的稳定触发，在触发系统中增设信号展宽电路，其作用是将Z脉冲信号宽度放大一倍，增加触发信号的可靠性。

考虑到减少测试系统的噪声，采用连续采集多圈数据平均的方法消除随机噪声，在系统中增加了NI PXI-6602[6-7]高速计数器模块，利用该计数器对光栅编码器Z相脉冲展宽信号进行计数，当采集持续到设定的圈数后，计数器停止并复位，采集任务自动结束，开始后续数据处理。

2.2 内时钟变采样定位测试关键技术

为确保测点定位采集精度，PXI-4462多功能数采卡采用

内部时钟作为采集时钟，采用动态变采样模式，采样频率fs取决于电容测微仪频响fc、转盘全周的采样点数N以及精密离心机的转速ω三个因素。三者关系如式(6)～式(7)所示。

在稳定转速ω下，设在转盘全周采集N个点，则采样频率fs由下式确定：

(6)

由上式可知，N值不变时，采样频率fs应随不同的转速ω变化。设电容测微仪的频响为fc，为使电容测微仪采集到有效信号，设离心机转动频率为rpm/min，则N应由下式确定，N取整数：

(7)

本项目中电容测微仪截止频率为8 kHz，令N值为1 600，则转盘圆周将被等分为1 600点，转盘的最大转动频率为5 Hz，则fs=8 kHz，当转盘的转动频率为1 Hz，则采样频率应设为1.6 kHz，依次类推。

3 动态半径测量结果

按照定位测试法开展了多次动态半径的测量，获取了精密离心机4个定位平台的动态半径测量原始值，某次典型测试的1#定位平台动态半径测量原始值如表2所示，动态半径随g值变化如图7所示。

表2 1#定位平台动态半径测量原始值表

图7 1#定位平台动态半径随g值的变化趋势图

由图7可知，1#动态半径随g值的变化基本呈线性关系，后续对数据进行处理，对测量不确定度进行评估，测量标准不确定度为σ=0.21 μm。

4 结论

本文介绍了一种适用于高精度精密离心机动态半径的外基准定位测试法，对定位测试技术的可行性进行了论证，结合变采样率数据采集技术，实现了动态半径的精确定位测量，实践表明，动态半径的测量标准不确定度为0.21 μm，测试稳定，可为更高精度精密离心机动态半径的测量提供参考。

[1] 凌明祥.精密离心机加速度测量模型研究[R].国防科研报告，GF-A0162889G，2012.

[2] 刘 健.线加速度模拟转台—离心机动态半径的测试研究[D].天津：天津大学，2007.

[3] 张 荣，王 珏，周继昆，等. 精密离心机动态俯仰失准角的定位测量技术研究[J].计算机测量与控制，2015，23(9)：2964-2967.

[4] 德国米铱有限公司.CapaNCDT-电容式位移传感器和测量系统[EB/OL].http://www.米铱.com/productsdetailed.aspx?cateid=13&productsid=41，2011.

[5] NI公司.NI PXI-4462四通道动态信号分析仪[EB/OL].http://sine.ni.com/nips/cds/view/p/lang/zhs/nid/14309，2012.

[6] 李 岳，王 燕，杨基明.多通道瞬态信号测试系统[J].电子技术应用，2008，8：8-9.

[7] 曾和荣，冯琦杰，谷振军，等.基于虚拟仪器技术的池式热堆Rossi-α测量装置设计[J].核科学与工程，2010，30(2)：110-113.

Research on Positioning Measurement Technique of Dynamic Radius of Precision Centrifuge

Zhang Rong, Wang Jue, Zhou Jikun, Zhang Yi, Zheng Min

(Institute of Systems Engineering, Mianyang 621900,China)

The dynamic radius affects the precision of acceleration outputted by precision centrifuge, it is a main technique parameter of precision centrifuge and should be measured accurately during the process of precision centrifuge design. Its value will be as compensation component to be added to the acceleration compensation mathematic model, then, the precision centrifuge can obtain acceleration value accurately. This paper introduces the dynamic radius test technique based on external reference, including multiple positioning data identification method of positioning platform, test system configuration and so on. The technique has been applied to the dynamic radius test of high precision centrifuge, the measurement results show that using the measurement technique, the standard deviation of the dynamic radius measurement is 0.21 μm, the measurement result satisfies the requirement of the high precision centrifuge technique indicators.

precision centrifuge；dynamic radius；positioning measurement；external reference

2015-12-26；

2016-01-29。

国家重大科学仪器专项(2011YQ130047)。

张 荣(1979-)，男，四川资阳人，工学硕士，高级工程师，主要从事环境试验技术、动态测试技术以及计算机软硬件开发技术方向的研究。

1671-4598(2016)07-0049-03

10.16526/j.cnki.11-4762/tp.2016.07.014

TP751 文献标识码：A