捷联惯导系统现场标定方法

高 伟，叶 攀，许伟通

(哈尔滨工程大学 自动化学院，哈尔滨 150001)

捷联惯导系统现场标定方法

高 伟，叶 攀，许伟通

(哈尔滨工程大学 自动化学院，哈尔滨 150001)

陀螺漂移会对捷联惯性导航系统的导航定位误差产生直接的影响，所以需要用实验的方法标定出陀螺漂移，并进行补偿；陀螺漂移随时间和环境变化，因此采用实验室标定方法会降低系统的精度；文章提出一种基于卡尔曼滤波技术的现场标定方法，给出了现场标定时系统的状态方程，分别推导了采用速度、速度加姿态为观测信息时的量测方程；利用奇异值可观测度分析方法比较机动状态不同，观测信息不同的五种现场标定方案的陀螺漂移的可观测度，从而确定了两种最优现场标定方案，即在以速度为外部观测量的情况下，使载体处于“S”型机动状态和在载体静止的情况下，速度加姿态为观测信息；通过仿真实验验证了这两种标定方案可以有效提高现场标定的精度。

捷联惯导系统；陀螺漂移；现场标定；卡尔曼滤波；奇异值

0 引言

在捷联惯导系统中，惯性测量组件直接安装在载体上，所以惯性测量组件的误差对捷联惯导系统的性能影响很大，特别是陀螺漂移对导航定位误差的影响按时间的三次方增长[1]。必须预先在实验室对陀螺漂移进行标定，然后在使用时加以补偿。由于实验室标定存在一定误差，并且随着时间和环境的变化，陀螺漂移存在变化，即一定的偏移，我们称为陀螺的逐次启动误差，所以对于高精度的捷联惯导系统在每次启动时，需要在初始对准的过程中进行现场标定。本文介绍了基于卡尔曼滤波技术的现场标定方法，提出了两种提高陀螺漂移可观测度的有效措施。

1 现场标定中的系统模型

1.1 系统的状态方程

二通道10个状态量的系统状态方程如下[2]：

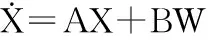
(1)

其中，X=[δVxδVyφxφyφz▽x▽yεxεyεz]T，δVx、δVy分为东向和北向速度误差；φx、φy、φz分别为x、y、z轴的平台误差角；▽x、▽y分别为x、y轴加速度计零偏；εx、εy、εz分别为x、y、z轴的陀螺漂移。A,B,W的具体设置见文献[2]。

1.2 系统的量测方程

分别以速度作为外部观测量和以速度加姿态作为外部观测量建立系统的量测方程。

1.2.1 以速度为外部观测量建立量测方程

以速度误差作为外部观测量时，系统的量测方程为：

(2)

其中:H1为量测矩阵

量测噪声η是零均值白噪声。

1.2.2 以速度加姿态为外部观测量建立量测方程

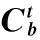
(3)

其中:p表示计算数学平台坐标系，另外有:

由(3)可知：

(4)

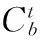
设捷联惯导系统输出的载体姿态角的测量值分别为ψI=ψ+δψ,θI=θ+δθ,γI=γ+δγ,则根据式 (3),(4)可得：

(5)

将式(5)右边按泰勒级数展开并忽略误差角的二次项得：

(6)

式(5)左边可以写为：

(7)

由于δψ是一个小量，可以近似认为tanδψ=δψ，则有：

(8)

将上式按泰勒级数展开，并忽略δψ二次项，得到:

(9)

又由:

连同(8) (9)可得：

(10)

同理可得:

(11)

令GPS测量的姿态角为ψGPS=ψ,θGPS=θ,γGPS=γ，则系统的量测方程为：

(12)

2 可观测度分析

为了分析比较不同方案下陀螺漂移估计的效果，以确定最优现场标定方案，利用奇异值可观测度分析法确定陀螺漂移在各现场标定方案下的可观测度。

2.1 奇异值可观测度分析法

因为可观测性分析不取决于输入激励[3]，因此可以将(1)(2)(12)表示的系统离散化，得到齐次模型如下：

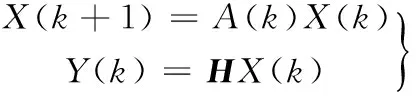
(13)

其中，量测矩阵Η为常值矩阵。

取一组观测值Y(0),Y(1),Y(2),…Y(k)，初始状态X(0)可以表示成观测值的函数。

(14)

令

得到:

(15)

其中:Rk是动态系统的提取可观测矩阵，初始状态X(0)的估计结果取决于Rk的奇异值[4]，将Rk进行奇异值分解：

(16)

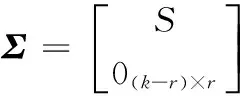
(17)

2.2 不同运动状态下的可观测度计算与分析

利用2.1节结论计算下面5种状态陀螺漂移可观测度。

方案1：以速度为观测量，静止状态。

方案2：以速度为观测量，加速运动。

方案3：以速度为观测量，三轴摇摆运动。

方案4：以速度为观测量，“S”型运动。

方案5：以速度加姿态为观测量，静止状态。

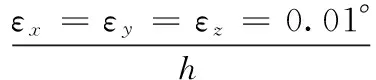
载体各运动状态下的运动参数设置如下：

(1)加速运动时，设载体以a=0.1 g的恒定加速度向东北方向加速运动，则ax=ay=0.070 7 g。

(2)摇摆运动由艏艉摇、纵摇、横摇、三种运动组合而成，摇摆轨迹可近似为正弦振荡，舰船的摇摆模型如下所示：

(18)

“S”型运动状态时，航向角周期变化的幅值为15°，周期为60 s，载体艏艉方向上的航速为10 m/s。

可观测度计算结果列表如下：

表1 可观测度计算结果

方案1与方案2水平陀螺漂移可观测，方位陀螺漂移不可观测；方案3 ,方案4,方案5水平陀螺漂移与方位陀螺漂移均可观测，对于方位陀螺漂移，方案5情况下可观测度最高，方案3情况下可观测度最低。从可观测度计算结果可以看出来，5种标定方案中，方案5的中的三轴陀螺漂移可观测度最高，理论上来说，陀螺漂移的估计精度也应该最高，即标定效果最好。

3 仿真分析

为了验证方案的可行性，进行数字仿真。利用Kalman滤波器在初始对准中对陀螺漂移进行滤波估计，Kalman滤波方程见参考文献[2]。

具体的标定方法为：

1)对舰船载体处于静止状态、加速运动状态、三轴摇摆运动状态以及“S”型运动状态下加速度计和陀螺仪的原始输出数据进行模拟；

2)在陀螺仪和加速度计输出的原始数据上加入陀螺常值偏移和加速度计零偏，其中，陀螺常值偏移设定为0.01°/h，加速度计零偏设定为1×10-4g；

3)由上一步中带有误差的陀螺仪和加速度计输出值通过惯导解算程序解算出系统的姿态误差和速度误差并将其带入本文第一、二两部分所述的卡尔曼滤波器中进行仿真；

4)分别画出本文2.2节所述的五种不同运动方案下的陀螺漂移的估计值的对比图，如图1至图4所述。

本次实验总的仿真时间为600 s，图中的纵坐标为陀螺漂移估计值与陀螺漂移真实值的比值。

图1是方案1和方案2下陀螺漂移的估计效果。两种状态下，水平陀螺漂移都可以估计出来，无明显差别；方位陀螺漂移的估计曲线都是发散的。

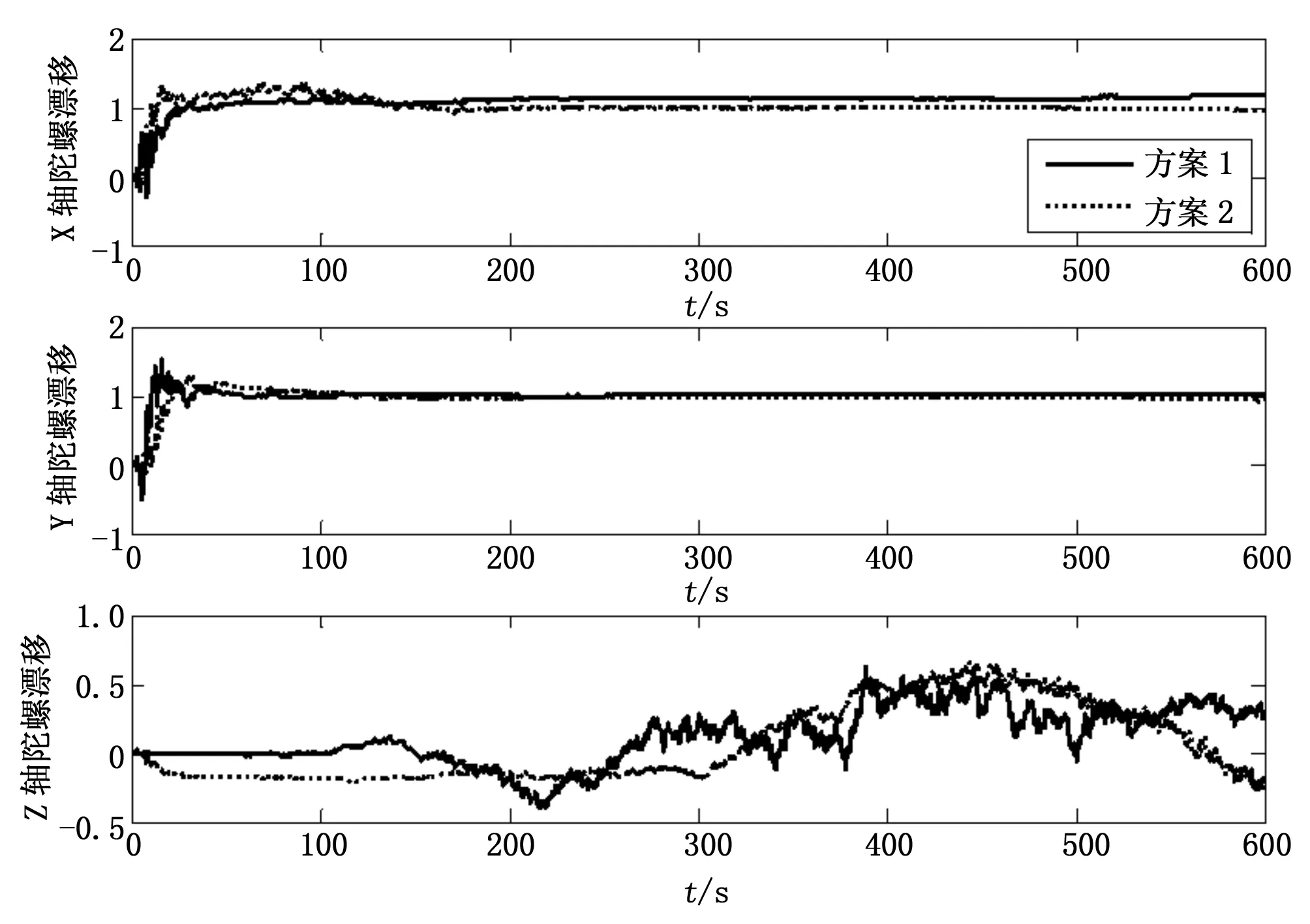
图1 方案1与方案2陀螺漂移的估计比较

图2是方案2和方案3下陀螺漂移的估计效果。方案3水平陀螺漂移的收敛速度比方案2收敛速度快；方案3方位陀螺漂移在较长时间内可以估计出来，但估计精度差，而方案2估计不出来。

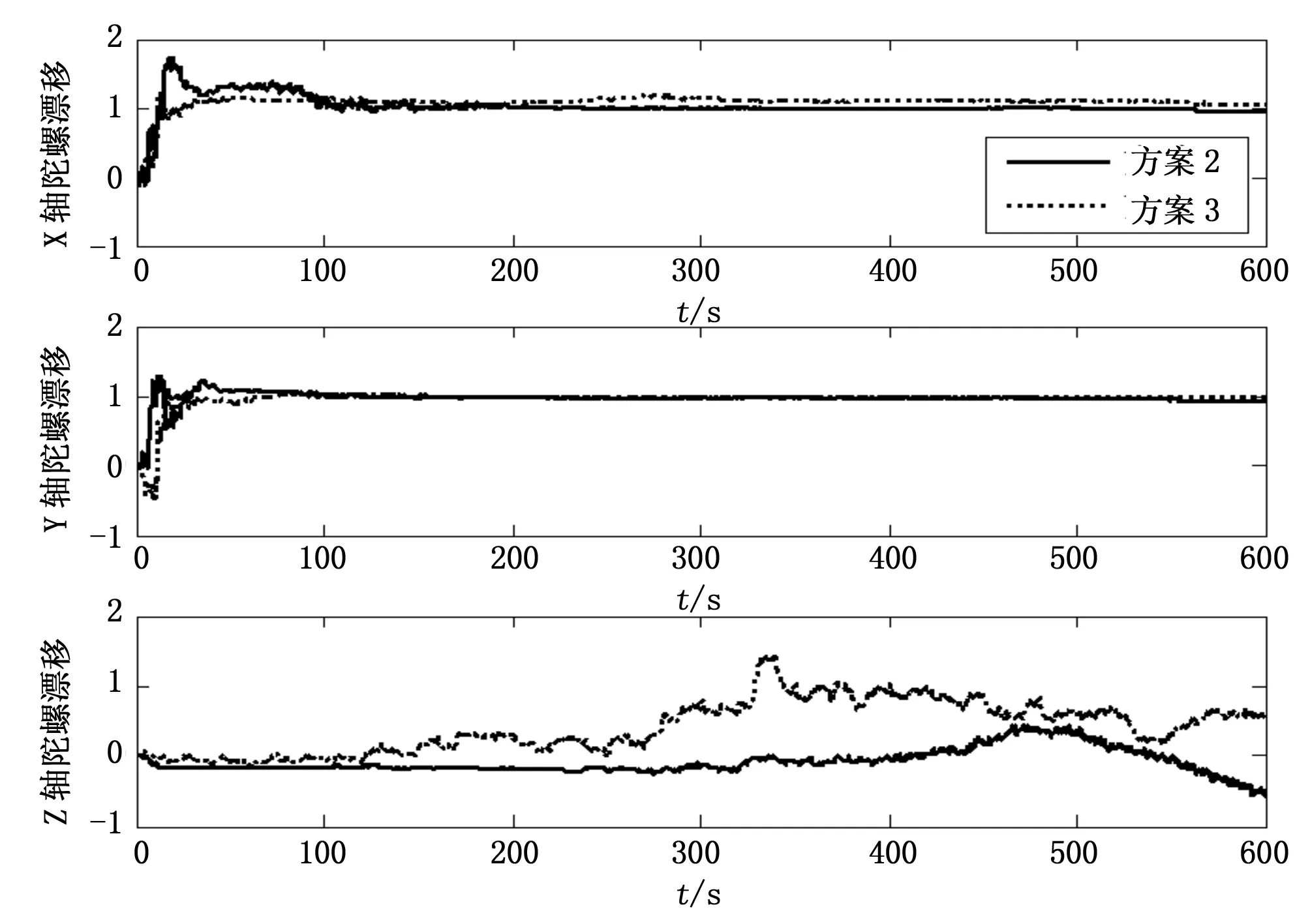
图2 方案2与方案3陀螺漂移的估计比较

图3是方案3和方案4下陀螺漂移的估计效果。两种状态的水平陀螺漂移估计效果相当；方案4方位陀螺漂移可以很好的估计出来，收敛速度比方案3快。

图3 方案3与方案4陀螺漂移的估计比较

图4是方案4和方案5下陀螺漂移的估计效果。 两种方案的水平陀螺漂移估计效果相当；方案5方位陀螺漂移估计精度和速度都要优于方案4。

图4 方案 4和方案5陀螺漂移的估计比较

综上，方案4和方案5均可作为现场标定方案，方案5优于方案4，并且仿真结果与2.2节可观测度的计算结果相吻合。

4 结论

为了完成现场标定的任务，分析了几种不同现场标定方案下陀螺漂移的可观测度，确定出两种最优的现场标定方案：在以速度为外部观测量的情况下，使载体处于“S”型机动状态；在不要求载体的机动性的情况下，增加系统的外部观测信息量即姿态信息。在组合对准阶段可实施上述两种现场标定方案，准确的估计出陀螺漂移。

[1] 尚 捷，顾启泰. 捷联惯导现场最优标定方法研究 [J]. 中国惯性技术学报，2005，13 (4)：18-21.

[2] 陈明辉. SINS误差特性及组合对准的方法研究 [D]. 哈尔滨：哈尔滨工程大学，2008.

[3] 程向红，万德钧，仲 巡. 捷联惯导系统的可观测性和可观测度研究 [J].东南大学学报，1997，27 (6)：6-11.

[4] Goshen-Meskin D, Bar-Itzhack I Y. Observability analysis of piece-of wise constant systems, part I: Theory [J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(4):1056-1067.

Field Calibration Method for Strapdown Inertial Navigation System

Gao Wei, Ye Pan, Xu Weitong

(Automation College, Harbin Engineering University, Harbin 150001, China)

Gyro drift has a direct impact on the navigation and positioning error of strapdown inertial navigation system, so it is necessary to calibrate the gyro drift with the experimental method. The gyro drift changes with time and environment, and the accuracy of the system can be reduced if the laboratory calibration method is used. This paper proposes a field calibration method based on Kalman filtering technique. State equation of calibration system is given directly, two measurement equations using velocity alone and velocity + attitude for the observation information are derived respectively. Singular value method is used to compute observability degree of gyro drift with different mobile states and different observation information of five field calibration schemes. Two optimal field calibration schemes that the carrier is in the “S” maneuver in case of using velocity for the observation information and the carrier is static in case of using velocity and attitude for the observation information are determined. Moreover, simulation experiments are implemented to verify the two schemes based on the field calibration method can effectively improve calibration accuracy.

strapdown inertial navigation system;gyro drift;field calibration;Kalman filtering;singular value

2015-11-23；

2016-02-15。

国家自然科学基金(51379042)；中央高校基本科研业务费专项资金(heucfq1404)。

高 伟(1977-)，男，黑龙江哈尔滨人，教授，博士，主要从事捷联导航技术、光学陀螺技术、海洋运载器综合导航技术方向的研究。

1671-4598(2016)07-0301-03

10.16526/j.cnki.11-4762/tp.2016.07.081

U666.1 文献标识码：A