初始残余应力对齿轮磨削后应力分布的影响*



初始残余应力对齿轮磨削后应力分布的影响*

齿轮广泛应用于机床、工程机械、船舶和航空等诸多领域[1]，其性能的优劣在一定程度上决定着整个产品的质量水平。齿轮失效多源自齿面或齿根的表面，因此齿面性能显得非常重要。磨削加工作为齿轮加工最重要的一道工序，对齿轮的表面性能起决定性的影响[2]。齿面残余应力与齿面精度对齿轮性能的影响尤为突出，当前者表现为压应力时，可以有效抵消齿轮工作过程中承受的拉应力载荷，提高齿轮寿命；后者对于齿轮运行平稳性、降低啮合时产生的噪声亦有着重要影响。

目前，主要采用有限元仿真方法对齿轮磨削过程进行研究。T. Altan与E.Ceretti[3]模拟了磨削过程中切屑的产生过程，给出了切削应力与应变的分布规律。P.N.Moulik等[4]对磨削过程中的热应力进行了研究，得出了热应力的影响因素。邓朝晖等[5]进行了WC/12Co材料的磨削残余应力的有限元求解，得到了不同磨削工艺参数下的磨削残余应力。黄强等[6]进行了磨削层温度场分布的有限元分析，给出了磨削温度场分布随时间的变化规律。

然而，大多数针对磨削开展的仿真分析忽略了初始残余应力的影响。由于磨削后齿面的应力分布是由初始残余应力与磨削过程产生的应力共同作用的结果，若初始残余应力分布不均匀，会影响齿轮在磨削时的应力释放，导致各部分变形量不协调，从而影响齿面精度。精确获取磨削前的初始残余应力分布，对于研究磨削后齿面的表面性能有着重要的意义。

齿轮磨削前的应力分布状态是由材料属性和热处理工艺决定的。由于齿轮的热处理过程是温度、组织转变和应力相互作用的复杂的非线性过程，并伴随塑性变形，所以采用解析法来获取残余应力几乎是不可能的[7]。目前，针对齿轮残余应力的测量主要有机械释放测量法和无损测量法等2种，前者需对齿轮进行破坏；后者检测费用昂贵，均有很大的局限性。

利用有限元仿真分析方法可以有效地解决残余应力的提取问题。本文利用有限元软件DEFORM-3D模拟了12Cr2Ni4A齿轮的热处理过程，得到了齿面残余应力分布，并将残余应力数值加载至齿轮上进行磨齿加工仿真，研究了初始残余应力对于磨削后齿面应力分布与变形的影响。在此基础上，给出了12Cr2Ni4A热处理淬火温度的范围，为齿轮热处理工艺改进提供了理论支持。

1 12Cr2Ni4A齿轮热处理仿真

1.1 热传导微分方程

根据傅里叶定律，齿轮热处理过程遵守能量守恒定律，包含内热源瞬态传热环境下的三维热传导微分方程为[8]：

式中，T是齿轮瞬时温度；t是时间；λ是材料热导率；ρ是材料密度；cp是材料的比热容；Q是塑性功生成热和相变潜能；γ是齿轮径向坐标；χ是轴向坐标。

有限元分析设定整个齿轮满足热传导方程，将整个空间域离散化，分成有限个单元，每个单元同时满足热传导方程。单元由若干节点组成，单元内部的每一点温度由节点温度与形函数的乘积得到，整个温度场也就可以由节点温度来表示。

1.2 基于DEFORM-3D的齿轮热处理仿真模型

DEFORM-3D软件拥有专用的热处理模块(Heat Treatment)，在模拟工件的热处理上有广泛的应用。本文选用模数为2.5 mm，齿数为40，压力角为20°的标准圆柱齿轮为研究对象，齿轮材料选用12Cr2Ni4A，其化学成分见表1。

表1 12Cr2Ni4A钢化学成分(质量分数) (%)

12Cr2Ni4A材料的航空齿轮热处理工艺为：正火→淬火→回火→渗碳→深冷处理→低温回火，工艺流程图如图1所示。

图1 12Cr2Ni4A热处理工艺流程图

由于齿轮是对称件，为了减小运算量，本文仅选取齿轮的部分进行仿真分析，齿轮的网格划分图如图2所示。

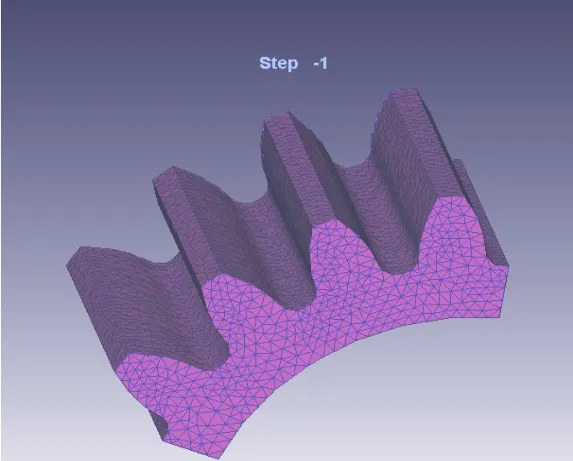
图2 齿轮热处理网格划分图

在DEFORM-3D软件中设置材料参数、热处理介质参数、工艺参数以及边界条件后，得到12Cr2Ni4A材料齿轮的热处理仿真结果。以马氏体含量为例，结果如图3所示。

图3 齿轮马氏体含量图

2 齿面残余应力提取

对于齿轮磨削加工，磨削前的齿轮残余应力的数值大小和分布状态，对磨削后齿面最终的残余应力分布以及齿轮变形均有着显著地影响。若要准确地获得磨削仿真后残余应力分布和变形情况，热处理后齿面残余应力的提取就显得尤为重要。

研究表明，在距齿面以下0.2 mm处，齿轮表面的残余应力的变化趋势趋近于零[9]。本文在热处理仿真结果的基础上，拟提取距齿面0.25 mm深度内的残余应力(假定热处理后齿轮内部的残余应力分布均匀)。以提取X方向的残余应力为例，选择“State Variables”中的“Stress—X”选项。在轮齿(厚度方向沿Z轴)的表面上选取任意一点Pe作为参考点，沿着该点的法线且朝向齿厚方向选取与Pe直线距离为0.25 mm的点Ps。将2个点之间均匀分成25份，得到间隔0.01 mm的各个点的应力值(见图4)。

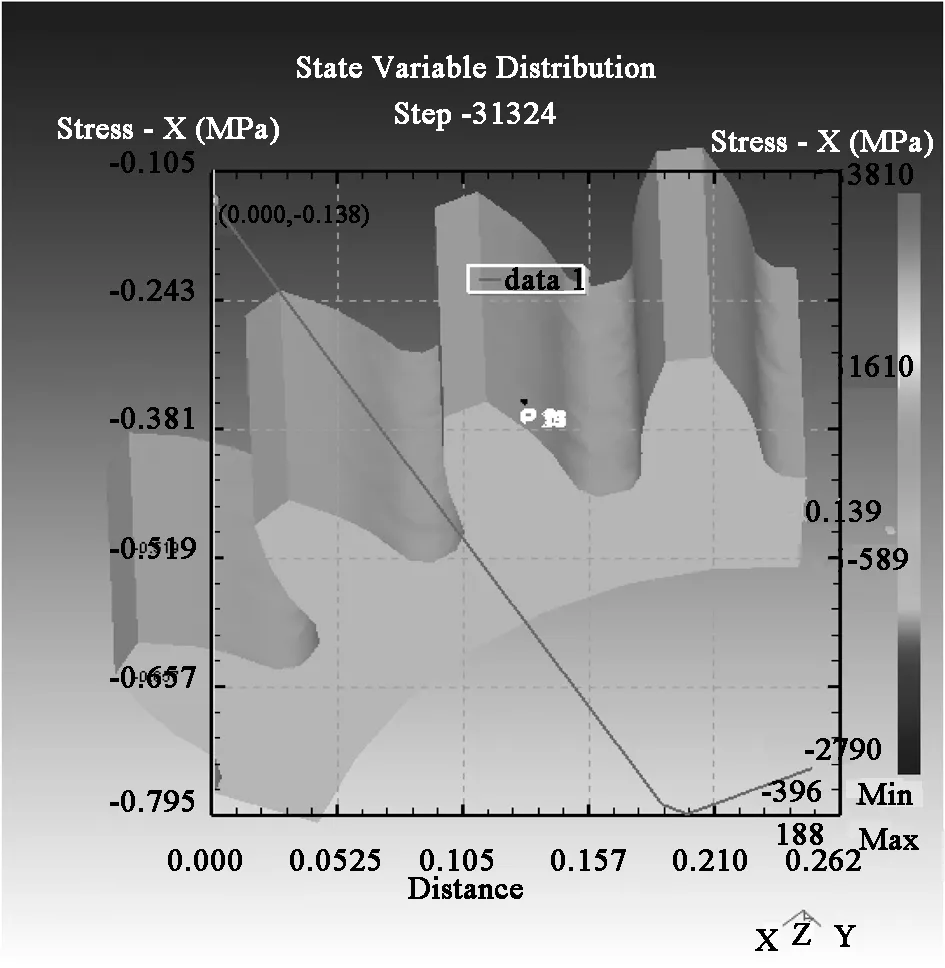
图4 X方向残余应力数值图

由图4中可以看到，距齿面以下0.20 mm处，残余应力变化趋势趋于平缓，这与文献[9]中所述是一致的。选择不同的Pe点，重复上述方法，得到其他4组沿X方向的齿面残余应力，取对应点应力的均值作为相应平(曲)面内沿X方向的残余应力值。

利用上述方法，得到其余5个方向的残余应力值，汇总后，得到距齿面以下0.25 mm内各个深度的残余应力分布(见表2)。

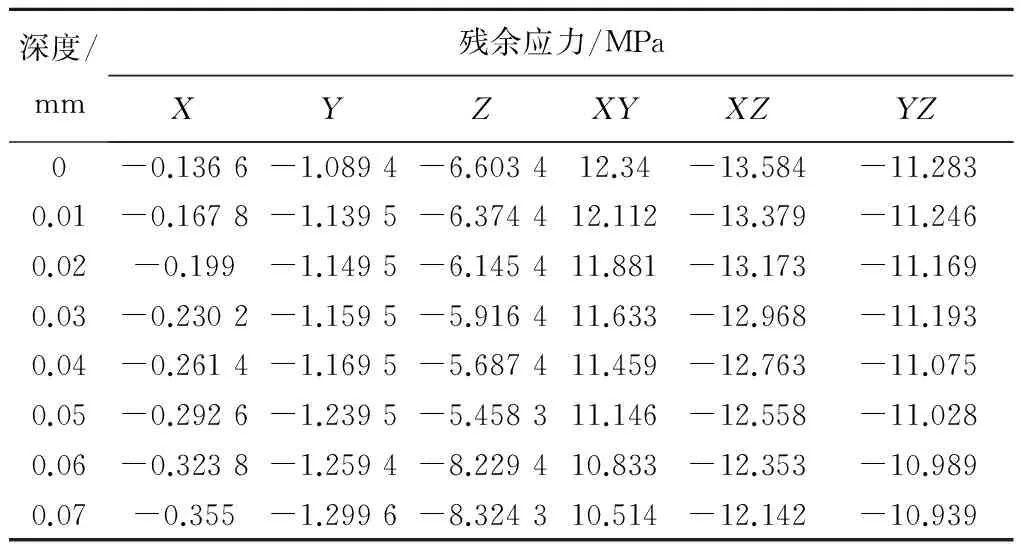
表2 齿面各深度内残余应力数值表

(续表)

3 多磨粒砂轮-齿轮磨削仿真分析

3.1 基于ABAQUS的多磨粒砂轮-齿轮磨削仿真模型

磨粒磨削工件的过程就是工件材料在磨粒作用下，形成弹性变形到塑性变形，直至断裂的过程。磨削过程达到稳态的时间极短，热量来不及传入整个齿轮就被切削液带走，由于距齿面以下0.2 mm处残余应力变化趋势已不明显，本文仅选取齿轮的一小部分作为研究对象。考虑到砂轮磨粒尺寸远远小于所选工件的尺寸，磨粒在齿面的磨削运动可近似由磨粒在平面上的磨削运动代替。本文选取距齿面以下0.25 mm的一小块长方体作为磨削仿真模型，其外形尺寸为1.75 mm×1.6 mm×0.25 mm，为统一坐标系，设工件厚度方向沿Z轴。

在砂轮实际磨削过程中，磨粒不是简单地以单颗磨粒的形式存在，而是许多磨粒随机地分布在砂轮表面。为了能够更真实地反应砂轮磨削过程，本文参考相关文献[10]，建立了基于随机分布的多磨粒砂轮有限元模型(见图5)。

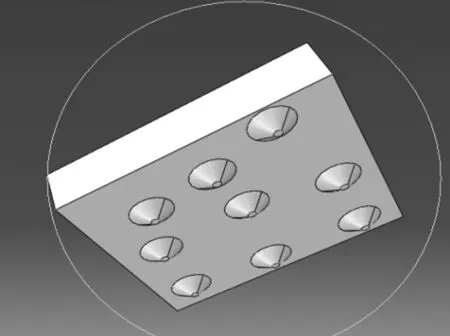
图5 多磨粒砂轮模型

假定磨粒为圆锥体，半锥角60°，高度0.180 mm，磨粒顶端部分磨损。砂轮磨粒材料采用CBN，粒度230#～270#。CBN磨粒性能参数见表3。

表3 CBN磨粒性能参数

磨削仿真过程伴随着网格畸变，属于高度非线性问题之一，显式时间积分更适合于求解动态非线性问题。另外，由于磨粒相对工件来说，强度、硬度都要高于齿轮材料，不会发生较大的变形，所以砂轮选用刚性体来模拟，以提高计算效率。

设砂轮磨削线速度为20 m/s,磨削深度为0.25 mm,进给速度为0.05 m/s,模拟齿轮粗磨过程，选取逆磨加工的方式。工件的网格单元选用C3D8RT类型，建立多磨粒磨削仿真模型如图6所示。

图6 多磨粒砂轮-齿轮磨削仿真模型

3.2 初始残余应力加载

沿着工件磨削深度方向每0.01 mm建立1层单元集合，共计25层集合；通过ABAQUS预定义场变量设置，依次把热处理仿真后获取的25组点的残余应力数值输入到相应单元集合上，完成磨削前的初始残余应力加载。以第1层单元为例，6个方向的残余应力加载图如图7所示。

图7 初始残余应力加载图

4 有限元仿真结果分析

4.1 初始残余应力对齿面残余应力的影响

在仿真结果中去除被磨削层，得到磨削后齿面残余应力分布云图(见图8)。

图8 齿面残余应力分布云图

忽略误差较大的工件边缘区域，计算每层节点应力的平均值作为该层残余应力值，沿磨削深度方向上的残余应力分布如图9所示。

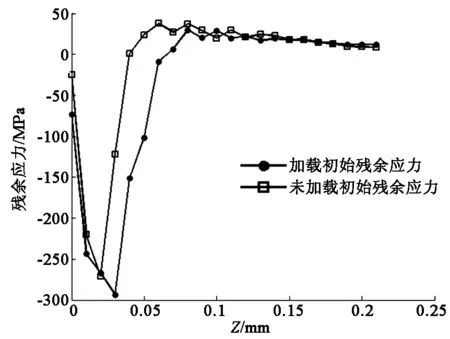
图9 残余应力沿工件深度分布图

未加载初始残余应力的齿轮残余压应力幅值为-271.43 MPa，残余压应力层厚度约为0.04 mm；加载初始残余应力后，齿轮残余压应力幅值为-293.64 MPa，残余压应力层厚度约为0.06 mm。应力幅值与压应力层厚度分别提高了8.18%和50%。当加载残余应力后，齿轮的应力分布更加精确，这对于准确评价齿轮应力分布状态以及精确预测齿轮寿命，有着重要的理论意义。

4.2 初始残余应力对齿轮塑性变形的影响

磨削后齿面塑性变形的大小，对齿轮啮合性能以及运行时的噪声大小有着重要地影响。计算每层节点塑性变形的平均值作为该层单元的塑性变形值，得到沿磨削深度方向上的齿轮塑性变形(见图10)。

图10 齿面塑性变形沿工件深度变化图

当加载初始残余应力后，齿面的塑性变形有一定的提高，并随着磨削深度的增加而逐渐趋近于零。这是因为齿轮在磨削过程中材料主要承受拉应力，而齿轮热处理后齿面残余应力以压应力为主，与未加载初始残余应力相比，加载初始残余应力的齿轮，磨粒拉断同样尺寸的材料需要施加更大的拉力来克服压应力，相应产生并传入齿轮的热量也随之增加，提高齿轮温升。对于同一材料而言，其温升越高，材料的抗变形能力就越差，即材料变“软”，产生的塑性变形也就越大。

显然，过大的塑性变形，不能满足齿轮表面完整性的要求。综合上述分析，热处理后齿面的残余压应力既可以提高齿轮的压应力幅值与压应力层厚度，进而提高齿轮寿命，也会使齿面的塑性变形随之增加，造成齿面精度下降；因此，热处理后的残余压应力过大或者过小均不满足齿轮的表面完整性要求，维持其保持在一个合理区间是十分必要的。

5 淬火温度对热处理后齿轮残余应力的影响

磨削后齿面呈现残余压应力状态，较大的残余压应力能够有效抵消齿轮在工作过程中承受的拉应力载荷。由上述可知，过大的残余应力伴随着的是较高的齿面塑性变形，因此，必须进行热处理工艺参数的优化，使齿面热处理后的残余压应力维持在一个合理区间。

在齿轮热处理过程中，淬火温度对齿轮残余应力的影响十分显著。本文利用DEFORM-3D软件，模拟了不同淬火温度下12Cr2Ni4A齿轮的热处理过程(见图11)。由图11可知，当淬火温度升高时，齿轮的残余应力值不断增大，但到了850 ℃以后，残余应力略有下降。其原因在于淬火温度的升高使得齿轮的热应力增加，残余应力呈现拉应力的增加趋势；另一方面，伴随淬火温度的升高，奥氏体晶粒尺寸不断增大，相变后的马氏体晶粒尺寸也随之增大，相变应力不断增大。残余应力是热应力与相变应力共同作用的结果，而当温度继续升高时，相变应力的变化趋于零，此时只有热应力起主导作用。

图11 淬火温度对齿面残余应力的影响

与此同时，随着淬火温度的升高，奥氏体晶粒尺寸逐渐变大，冷却后得到的马氏体的晶粒较粗大，其韧性、强度随晶粒尺寸的增加而显著下降。经过分析，当12Cr2Ni4A材料的淬火温度保持在810～840 ℃时，淬火后所产生的残余压应力能够较好地满足磨削后齿面对残余应力和变形量的要求，且此时淬火后生成的马氏体组织主要呈针状，满足齿轮对韧性、强度的要求。

6 结语

综上所述，可以得到如下结论。

1)建立了12Cr2Ni4A材料的热处理仿真模型，提出了一种精确获取齿面残余应力数值的方法，为进行磨削仿真分析提供了初始残余应力数据。

2)建立了多磨粒磨削有限元仿真模型，得到考虑初始残余应力的磨削后齿面残余分布与塑性变形情况。相比未考虑初始残余应力的仿真模型，加载初始残余应力后的模型其残余应力在幅值和压应力层厚度上有明显提高，其塑性变形亦随之提高。

3)从优化热处理工艺的角度，研究了淬火温度对热处理后齿面残余应力的影响规律，综合淬火温度对材料性能的影响，给出了12Cr2Ni4A热处理时淬火温度的合理区间。

[1] 刘国虎,陈羿.渗碳齿轮的热处理分析[J].新技术新工艺，2016(1)：98-100.

[2] 高玉魁,赵振业.齿轮的表面完整性与抗疲劳制造技术的发展趋势[J].金属热处理，2014，39(4)：1-6.

[3] Ozel T，Altan T. Determination of workpiece flow stress and friction at the chip-tool contact for high-speed cutting [J].Int.J. Mach. Tools Manuf.，2000，40(1)：133-152.

[4] Moulik P N， Yang H T Y， Chandrasekar S. Simulation of thermal stress due to griding[J]. International Journal of Mechanical Science, 2001, 43(3)：831-851.

[5] 邓朝晖,荆琦,安磊.纳米结构WC-12Co涂层精密平面磨削表面残余应力有限元模拟与试验[J].机械工程学报，2008(7)：58-60.

[6] 黄强,赵秀栩.磨削温度场中的数值模拟方法研究[J].中国水运，2007(5)：30-31.

[7] 何庆稀. 钛合金TC11毛坯热处理过程数值模拟[J].机电工程，2008，25(5)：104-106.

[8] 朱海龙,李世芸,王春荣. 齿轮零件淬火过程温度场的数值模拟[J].新技术新工艺，2014(3)，106-108.

[9] 陈云龙.基于残余应力控制的大功率螺旋锥齿轮磨削加工技术[D].北京：北京航空航天大学，2015.

[10] 张祥雷,姚斌.基于多颗磨粒随机分布的虚拟砂轮建模及磨削力预测[J].航空学报，2014，35(12)：3489-349.

国家自然科学基金资助项目(51275020)

国家高科技支撑项目(2014BAF08B01)

责任编辑 马彤

王延忠1, 李 岩1,刘 旸1，赵兴福2

(1.北京航空航天大学 机械工程及自动化学院，北京100191；2.中航工业哈尔滨东安发动机(集团)有限公司 工艺技术部，黑龙江 哈尔滨 150001)

磨削作为齿轮加工的重要工序，对齿轮的精度和应力分布有决定性的影响，然而大部分关于齿轮磨削的研究极少考虑初始残余应力的影响，使得分析结果的准确度有所降低。利用有限元方法模拟了齿轮的热处理过程，获取了齿轮磨削前的初始残余应力，在此基础上进行了齿轮磨削仿真，得到了考虑初始残余应力的齿面残余应力分布和齿轮变形情况，给出了12Cr2Ni4A齿轮淬火温度的最佳区间。为精确获取齿轮磨削后的应力与变形情况提供了一种方法，同时为优化齿轮的热处理工艺提供了理论参考。

齿轮磨削；初始残余应力；齿面变形；有限元方法

Influence on Stress Distribution of Initial Residual Stress after Gear Grinding

WANG Yanzhong1， LI Yan1， LIU Yang1， ZHAO Xingfu2

(1.School of Mechanical Engineering and Automation of Beihang University， Beijing 100191， China；

2.Technology Department of Avic Harbin Dongan Engine (group) Co., Ltd., Harbin 150001， China)

As an important working procedure of gear machining, the grinding process has a decisive influence on the precision and stress distribution of the gear. However, most of the research on gear grinding rarely considers the fluence of initial residual stress, which results in lowering the precision of analytical results. Use the finite element method simulating the process of heat treatment of gear and gains the initial residual stress. On the basis, it accomplishes the gear grinding simulation considering the initial residual stress, and gets residual stress distribution and gear deformation distribution of the tooth surface, then also optimizes hardening heat of 12Cr2Ni4A. Offer a method to gain the deformation and stress distribution of the gear after grinding, and provide a theoretical reference for optimizing heat treatment process of the gear.

gear grinding， initial residual stress， gear surface deformation， finite element method

王延忠(1963-)，男，教授，主要从事先进精密传动加工技术、空间啮合曲面数字加工理论和技术、传动摩擦学理论与应用技术、面向可再生能源的高效绿色传动装备技术和大型数控装备技术等方面的研究。

2016-04-06

TH 132.413

A

* 航空A计划资助项目(ATR-125-02-101)