级配碎石基层塑性变形预估模型

2023-01-18刘广坤陈峙峰郭宏伟李小东陈忠达

土木工程与管理学报 2022年6期

刘广坤, 陈峙峰, 郭宏伟, 李小东, 陈忠达

(1. 河南中州路桥建设有限公司，河南周口 466002; 2. 周口市公路勘察设计院，河南周口 466000;3. 河南宏盛工程监理有限公司，河南周口 466000; 4. 中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122; 5. 长安大学特殊地区公路工程教育部重点实验室，陕西西安 710064)

级配碎石基层设置于半刚性基层与沥青面层间，可有效抑制半刚性基层收缩裂缝引起的沥青面层反射裂缝[1～4]。然而级配碎石易产生较大塑性变形[5～7]，引起沥青路面的过大变形，导致级配碎石基层破坏甚至整个路面结构破坏，因此有必要研究级配碎石基层塑性变形规律并建立预估模型。国内外学者已开展了粒料材料的变形预估研究。魏密[8]通过重复荷载动三轴试验，按分层总和法建立了粒料材料永久变形预估模型；马士杰[9]采用含水率与模量拟合模型参数，建立了基于应力状态的永久应变预估模型；李頔[10]通过动三轴试验分析轴向应变与加载次数的关系，建立了级配碎石永久变形累计方程；Wolff和Visser[11]基于实体工程加载试验，建立了级配碎石基层变形预估模型；Pérez等[12]根据粒料材料永久变形三轴重复加载试验，建立了基于荷载作用次数和应力比的永久变形预估模型，见式(1)。研究发现[8,9]，粒料材料塑性变形规律更符合Pérez预估模型。

ε1p=ANB+(CN+D)(1-e-EN)

(1)

式中：ε1p为累积轴向永久应变；N为荷载作用次数；A,B,C,D,E为与应力水平相关的系数。

本文以Pérez预估模型为基础，提出级配碎石初始塑性应变预估模型，通过塑性变形试验结果标定模型系数；考虑到级配碎石基层的实际受力状况各异，以0.7 MPa应力水平为标准，把不同应力水平下的级配碎石塑性变形量换算为标准应力水平(0.7 MPa)下的级配碎石塑性变形量；最后建立考虑荷载作用次数和应力水平的级配碎石基层塑性变形预估模型。

1 初始塑性应变预估模型的提出

研究表明Pérez预估模型更加合理、可靠，因此本文基于此模型，以初始塑性应变为因变量，建立级配碎石初始塑性应变预估模型，见式(2)。需说明的是，初始塑性应变εp是指应力p下级配碎石t时刻的塑性变形量与其第60 min的塑性变形量的比值。

(2)

式中：dt,p为p应力水平作用下级配碎石t时刻的塑性变形量(mm)；d60,p为p应力水平作用下级配碎石第60 min的塑性变形量(mm)；h为级配碎石基层厚度(mm)；hs为级配碎石试件厚度，取为100 mm。

式(2)所示的预估模型中，模型系数A，B，C，D，E根据塑性变形试验结果进行标定；级配碎石第60 min的塑性变形量d60,p通过塑性变形试验确定。

2 塑性变形试验

试验采用的集料由陕西石灰岩加工而成，技术性能符合JTG/T F20—2015《公路路面基层施工技术细则》的要求[13]，级配见表1。振动击实试验得到，GM级配的最佳含水率为3.40 %，最大干密度为2.47 g/cm3；GF级配的最佳含水率为3.60%，最大干密度为2.44 g/cm3。采用轮碾仪成型长300 mm×宽300 mm×厚100 mm的试件，试件密度为最大干密度的98%。试验状态分为最佳含水率状态和饱水状态两种，其中最佳含水率状态指试件成型后(不脱模)在室内放置4～5 h，即进行塑性变形试验(此时试件含水率接近最佳含水率，故称之为最佳含水率状态)；饱水状态指试件成型后(不脱模)在室内放置4～5 h，再将试件连同试模在水中浸饱24 h，然后进行塑性变形试验(由于浸饱24 h，试件含水率达到饱和状态，故称之为饱水状态)。

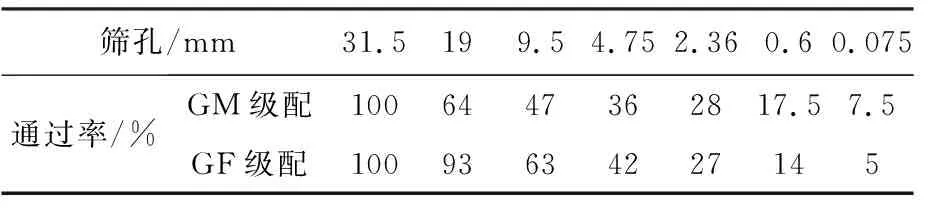
表1 集料级配

塑性变形试验借助车辙试验仪进行，在此称其为塑性变形试验仪。试验参数为：试验轮行走距离为230 mm，试验轮往返行走速度为42次/min；试验轮轮压为0.5，0.6，0.7，0.8，0.9 MPa，其中0.7 MPa为标准轮压；试验历时60 min，其中前10 min为预压，后50 min为正式试验。

塑性变形试验方法与沥青混合料车辙试验相似，试验时将试件连同试模放置于试验台上，试验轮位于试件的中央部位，其行走方向与试件碾压方向一致，如图1所示。仅在正式试验时记录级配碎石试件的塑性变形量。图2为塑性变形试验前后的试件状况，塑性变形试验后有明显的辙槽印。

图1 塑性变形试验示意/mm

图2 塑性变形试验前后的试件状况

3 塑性变形预估模型的建立

分别进行不同级配、不同试验状态和不同试验轮压(应力水平)的级配碎石塑性变形试验，试验结果从略，以此来标定模型系数A，B，C，D，E。

3.1 模型系数的标定

根据不同级配(GM级配和GF级配)、不同试验状态(最佳含水率状态和饱水状态)、不同应力水平(0.5,0.6,0.7,0.8,0.9 MPa)的塑性变形试验结果按式(2)进行回归分析，即得模型系数标定结果，见表2～5。

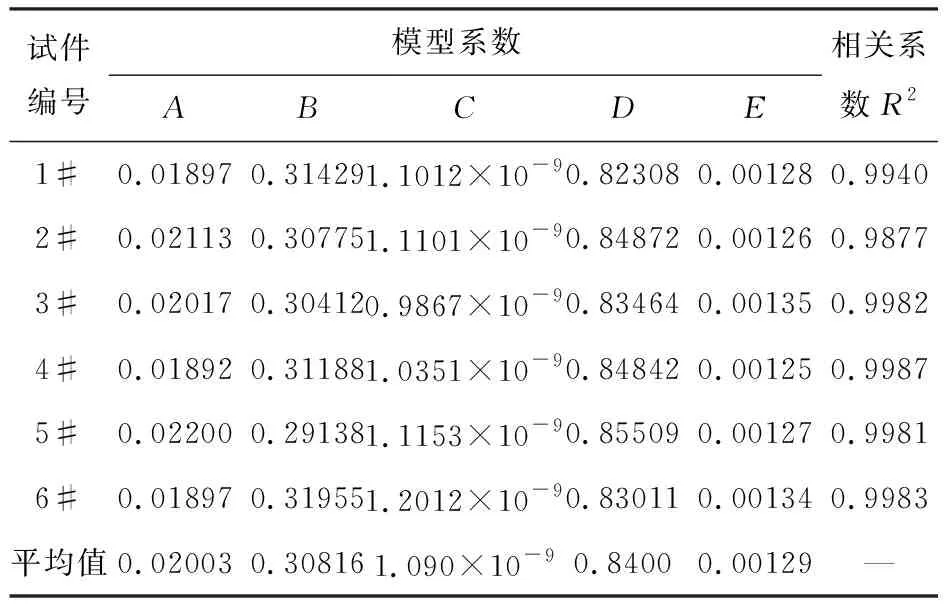
表2 最佳含水率状态下GM级配碎石模型系数标定结果

表3 饱水状态下GM级配碎石模型系数标定结果

表4 最佳含水率状态下GF级配碎石模型系数标定结果

表5 不同应力水平下GM级配碎石模型系数标定结果

众所周知，级配碎石塑性变形受自身的含水率、级配和应力水平的影响较大，但其变化规律十分相似，即初始塑性应变基本不受含水率、级配和应力水平的影响，表明初始塑性应变εp具有相似的预估模型，表现为级配、试验状态和应力水平对模型系数的标定结果的影响不大，表2～5各种状态下的模型系数标定结果证明了这一点。

因此在模型系数标定时，不考虑这些因素的影响。综合不同级配、不同试验状态和不同应力水平下的塑性变形试验结果，模型系数的最终标定结果见表6。图3中GM级配碎石在0.7 MPa压力作用下，初始塑性应变的实测值和预估值十分接近，说明模型系数的标定结果是合理、可靠的。

图3 级配碎石初始塑性应变曲线(0.7 MPa压力下)

表6 级配碎石模型系数标定结果

3.2 塑性变形量d60,p的计算

塑性变形试验以0.7 MPa为标准轮压，但级配碎石基层的受力状况因受路面结构和设计参数的影响而各异。因此需将0.7 MPa标准轮压ps下的第60 min的塑性变形量d60,ps(简记为d60)等效转化为p应力水平下第60 min的塑性变形量d60,p。

理论研究表明，塑性变形比与应力比之间存在如下关系。

(3)

式中：α为塑性变形比系数；pr,pm为荷载应力(MPa)；dr,dm分别为pr,pm应力下的塑性变形量(mm)。

为建立塑性变形量等效换算关系，以GM级配碎石为分析对象，以第15,30,45,60 min的塑性变形量为指标，进行不同应力水平(0.5,0.6,0.7,0.8,0.9 MPa)下的塑性变形试验，结果见表7。

表7 不同应力p作用次数N的塑性变形量

以0.7 MPa应力为标准，按式(3)计算不同应力下的塑性变形比系数，结果见图4。

图4 塑性变形比系数α与应力p的关系

图4表明，塑性变形比系数α与应力水平p呈近似线性关系，其线性回归结果见表8。

表8 塑性变形比系数α与应力p回归结果

则塑性变形比系数α与应力水平p的关系为：

α=1.430p+0.261

(4)

将式(4)代入式(3)，即得应力水平p下级配碎石第60 min的塑性变形量d60,p：

(5)

根据式(5)即可计算应力水平p下级配碎石第60 min的塑性变形量。

3.3 塑性变形预估模型的确定

将式(5)、表6模型系数、hs=100 mm代入式(2)，并将dt,p简记为d，即得如式(6)所示的级配碎石基层塑性变形预估模型。

按式(6)即可预估级配碎石基层的塑性变形量。但当级配碎石基层厚度较大时，会影响计算结果精度。为此将级配碎石基层分成若干层，采用分层总和法来计算级配碎石基层的塑性变形量，其中分层厚度hi不宜大于100 mm。那么最终的级配碎石基层塑性变形预估模型见式(7)。

d=[0.02087N0.3150+(1.078×10-9N+

(6)

(7)

式中：di为级配碎石基层第i分层塑性变形量(mm)；hi为级配碎石基层第i分层厚度(mm)；d60为试验轮标准轮压(0.7 MPa)下级配碎石第60 min的塑性变形量(mm)；pi为级配碎石基层第i分层层中竖向压应力(MPa)。

4 预估模型的应用

某级配碎石(GM级配)基层沥青路面结构见图5，试预估级配碎石基层在1.0×107当量轴次作用下的塑性变形量。

图5 路面结构示意

级配碎石基层塑性变形量预估过程如下：

(1)计算级配碎石基层层中竖向压应力pi。级配碎石基层划分为两层，上分层h1=80 mm、下分层h2=100 mm。计算标准轴载ps作用于沥青路面路表时，级配碎石基层各分层层中竖向压应力pi，结果见表9，表中还给出了各分层层顶、层底竖向压应力。表9显示层中竖向压应力与其层顶和层底平均值十分接近，故式(7)中采用各分层层中竖向压应力作为该分层的竖向压应力。由此，本实例中，p1=0.130 MPa,p2=0.112 MPa。