基于共振分析的发动机附件传动系统危险齿轮的确定

欧阳旭靖，郭　梅，王建军

（1.北京航空航天大学能源与动力工程学院，北京100191；2.中航工业沈阳发动机设计研究所航空发动机动力传输航空科技重点实验室，沈阳110015）

基于共振分析的发动机附件传动系统危险齿轮的确定

欧阳旭靖1，郭梅2，王建军1

（1.北京航空航天大学能源与动力工程学院，北京100191；2.中航工业沈阳发动机设计研究所航空发动机动力传输航空科技重点实验室，沈阳110015）

为了确定某典型发动机附件机匣齿轮系统危险齿轮，对附件机匣各齿轮进行模态计算，通过行波共振分析获得共振Campbell图，初步得到危险齿轮编号。采用等效有限元法建立齿轮系统有限元模型，计算研究齿轮系统共振特性，确定工作转速内可被激起的危险共振模态，通过应变能法确定危险齿轮从而对单齿轮分析结果进行补充。结果表明：所提出的方法和技术能够有效确定复杂附件传动系统危险齿轮，从而大幅减少设计时间，并可为试验测量和故障分析提供参考。

危险齿轮；附件机匣；共振分析；齿轮系统；单齿轮；航空发动机

0　引言

附件齿轮传动系统作为航空发动机重要的传动装置，其可靠性对于发动机性能具有重要影响。发动机性能指标不断提高，航空齿轮薄壁结构的轻薄化设计使得轮体结构的振动疲劳破坏成为主要失效模式之一。为了保证齿轮系统工作可靠性，在设计过程中需要分析齿轮系统振动特性并进行试验验证，而附件机匣为多个齿轮轴组成的复杂长链式系统，各齿轮载荷环境和共振特性不相同，系统分析每个齿轮会延长设计周期。因此在不同环境下，确定可能产生共振从而引起疲劳破坏的危险齿轮，将其作为结构设计、响应分析、疲劳特性研究的主要对象，对于提高设计效率具有重要意义，同时也可为试验测量和故障分析提供参考［1-2］。

附件机匣齿轮系统特别复杂，研究其振动问题成为发动机设计过程中的重要环节。国外在齿轮箱的理论设计和试验研究方面做了大量工作，Hanjun Jiang和Yimin Shao［3］研究了考虑啮合刚度齿轮系统振动特性，表明齿轮系统啮合相位角对振动响应具有明显影响；Jian Lin和Robert G.Parker［4］研究了啮合刚度变化对2级齿轮系统振动问题的影响，分析说明了啮合相位角对齿轮系统振动影响很大，同时参数不稳定性也比单级齿轮系统的更复杂；也有大量学者［5-6］对齿轮系统减振降噪设计进行了研究。可见复杂齿轮系统振动问题已受到广泛关注。中国在分析解决多次出现的附件机匣振动破坏问题过程中积累了大量经验。宋乐民［7］对发动机中央传动锥齿轮试验机理进行了试验研究；杨荣等［8］在某型航空发动机附件机匣中心传动锥齿轮故障断裂分析中发现行波振动可能导致严重故障，有必要对齿轮系统进行行波共振分析；郭梅等［9-10］对附加机匣齿轮系统进行振动特性分析时发现，由于附加机匣是复杂的多部件组合弹性系统，多频率、多啮合的激励导致系统的振动设计和共振特性更为复杂，不易分析。目前大部分学者主要对某一问题进行深入分析，而关于危险齿轮确定的研究相对较少。李占营［11］对2级圆锥齿轮系统进行了有限元分析，通过共振转速图给出了简单避振方案，但并未系统地给出危险齿轮的确定方法。

本文基于共振分析，结合行波共振分析方法及应变能法，提出了1个危险齿轮确定方案，并确定了某典型航空发动机附件机匣齿轮系统危险齿轮。对附件机匣内各齿轮进行模态计算及行波共振分析，初步确定工作转速内可能出现危险共振模态的齿轮，建立齿轮系统等效模型，进行应变能分析验证行波共振分析初步确定的危险齿轮是否准确，并给出最终确定方案。该分析过程仅需对齿轮进行模态计算，耗费时间较少，之后谐响应分析及试验验证仅需集中于危险齿轮，可大幅缩减振动设计时间及成本。

1　附件机匣齿轮系统和危险齿轮确定方法

1.1附件机匣齿轮系统

典型航空发动机附件机匣齿轮系统由1002～ 1011号10个直齿圆柱齿轮组成，其中1006号齿轮为双联齿轮，系统简化如图1所示。传动系统如图2所示。

图1　齿轮系统简化

齿轮轴系统主要参数见表1。系统动力由1005号齿轮轴输入，经由各齿轮传给相应附件。

从表可见，各齿轮啮合激励频率分为2部分，分别为10385和4534 Hz，本文根据啮合激励频率将齿轮系统各齿轮分为上下2个分支（图2中虚线方框）。

图2　传动系统

表1　齿轮轴主要参数

1.2齿轮系统激励特性

齿轮工作中所受激振力主要为轮齿啮合激励力，其频率f可通过齿轮工作转速N/（r/min）及齿数z计算得出。由于主动轮和从动轮所受啮合激励力的频率相同，故以主动轮为例进行计算。

在齿轮传动过程中，激励力主要由啮合齿面、支承平面和输入输出端套齿产生，分别对3个部分激励特性进行说明。

在略去齿面间摩擦力的情况下，啮合齿面啮合力仅为啮合平面内的法向力Fn，Fn的方向与啮合线重合，可以分解为切向力Ft和径向力Fr2个分力，而在直齿圆柱齿轮系统轴向方向没有激励力，如图3所示。

支承处啮合力主要由齿面啮合力牵引导致，由于直齿轮齿面啮合力不存在轴向力，因此支承平面内仅产生径向力。

图3　齿轮啮合平面受力情况

齿轮系统在给附件传递扭矩和功率过程中，会在输入输出轴套齿齿面上产生周向力，而惰轴则不产生周向力。

1.3危险齿轮确定方法

确定危险齿轮分2步：单个齿轮行波共振分析和齿轮系统共振分析。

通过单个齿轮行波共振分析，判断齿轮在工作时是否可能发生共振，同时可确定共振的频率、阶次及转速等。由于轮齿啮合的存在，齿轮系统中各齿轮间不可避免的存在耦合作用，使得单个齿轮主导振动模态固有频率发生变化，同时伴随产生耦合振型，而单个齿轮行波共振分析无法对耦合作用进行评价。通过对齿轮系统进行共振分析，可以对单个齿轮行波共振分析结果进行补充，从而准确确定危险齿轮。

危险齿轮确定方法的流程如图4所示。

图4　危险齿轮确定流程

单个齿轮共振分析分2步：结合激励特性及模态振型，研究各类模态是否能被激起；通过行波共振分析，确定常用工作转速范围内是否出现共振模态作为危险齿轮判断依据。

齿轮系统共振分析分3步：结合激励特性研究各类共振模态能否被激起；将可被激起的各阶共振模态绘制到共振转速图中，确定常用工作转速区间内出现的共振点；通过对各共振点的共振模态进行应变能分析，确定常用工作转速范围内最可能出现共振的齿轮，即为危险齿轮。

2　单齿轮共振分析确定危险齿轮

2.1附加机匣单齿轮有限元模型

附件机匣齿轮系统由10个齿轮组成，在UG 8.0中分别建立各齿轮的3维实体模型，并在ANSYS中采用solid185单元建立有限元模型。各齿轮材料属性均为：弹性模量E=1.94×1011 Pa，密度ρ=7860 kg/m3，泊松比ν=0.297。由于齿轮数较多，因此给出上下分支的1004号齿轮和1007号齿轮的有限元模型举例说明，如图5、6所示。其中1004号齿轮的单元数为71004，节点数为100528；1007号齿轮的单元数为93056，节点数为130176。

图5　1004号齿轮模型

图6　1007号齿轮模型

根据实际工作条件施加边界条件，在滚棒轴承支承表面各节点施加径向约束；在滚珠轴承支承表面各节点上施加径向和轴向约束；在工作过程中齿轮转动自由度无约束，因此放开周向自由度。

图7　节圆扭转振动

2.2机匣传动系统齿轮模态振型特性

通过对上述附加机匣各齿轮进行模态计算，得到相应的固有频率和模态振型。下面将通过对模态振型进行分类［12］，并结合1.2节的激励特性及各类模态激振条件分析振动能否被激起。

根据振动位移分布，可以将单齿轮模态振型分为3类：轮体主导的振动，齿轮轴主导的振动及耦合振动。

轮体主导的振动根据振动方向可分为以下3种。

（1）周向扭转振动，其模态振型如图7所示。这类振动主要由轮齿啮合产生的切向力激起，根据1.2节激励特性分析可知，典型附件机匣齿轮系统存在周向力，因此这类振动可被激起。

（2）径向伸展振动，其模态振型如图8所示。激振条件为轮体上的径向力，附件机匣齿轮系统啮合时存在径向力，因此这类振动可被激起。

（3）轴向振动，振型如图9～11所示。由于仅轴向激励力可激起该类振动，而本文分析的典型附件机匣齿轮系统不存在轴向力，因此这类振动不会被激起。

图8　径向伸展振动

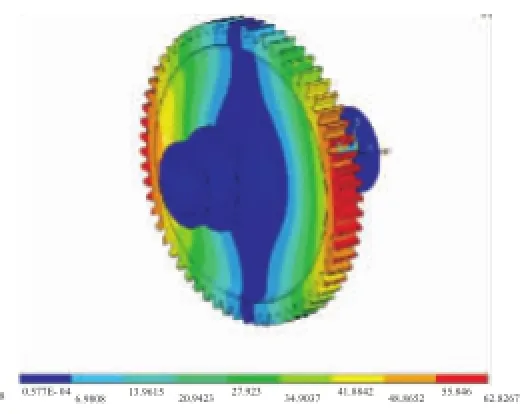
图9　节径对折振动

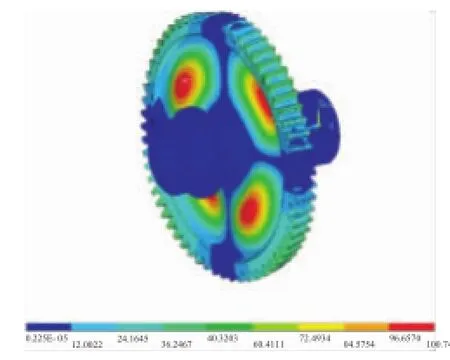
图10　节径节圆耦合振动

图11　节圆伞形振动

齿轮轴主导的振动分为2类。

（1）扭转振动，振型如图12所示。振动由齿轮轴上的周向力引起，根据激励特性分析，可知仅当振动发生在输入、输出轴对应套齿端时才可被激起；

（2）周波振动，振型如图13所示。这类振动主要发生在齿轮轴自由端，而自由端不存在激励力，因此这类振动被激起的可能性较低。

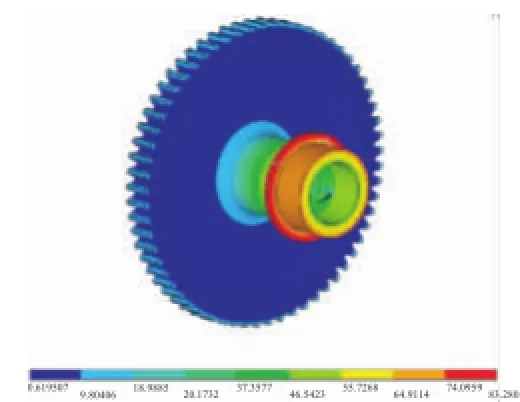
图12　齿轮轴扭转振动

图13　齿轮轴周波振动

耦合振动的形式较为复杂，难以判断，根据典型附件机匣齿轮系统不存在轴向力的特性，可知当耦合振动的主要振动方向为轴向时，不会被激起，这类振型如图14所示。

图14　耦合振动

2.3基于行波共振分析危险齿轮的确定

2.3.1行波共振分析原理

根据文献［13］可知，齿轮行波共振分析是齿轮设计过程中的重要环节，对于避免齿轮共振具有重要指导意义。在共振分析采用静止坐标系时，齿轮的节径型振动是前、后行波节径型振动，其固有频率随转速变化，见式（2）、（3）。

式中：ff、fb分别为齿轮旋转时，从静坐标上看到的顺、逆齿轮转向的前后行波固有振动频率；fd为齿轮旋转时，从与齿轮同转速同向旋转的动坐标上看到的齿轮振动固有频率，简称动频；齿轮不转时的固有频率称为静频，以f表示；m为节径数。

由1.2节可知，齿轮的激振频率随转速变化，变化关系见式（1）。通过绘制前后行波与激振频率随转速的变化曲线，得到共振Campbell图，由2种线的交点可直观看出共振频率和共振转速，从而确定可能的共振模态。

2.3.2单齿轮危险齿轮确定

根据行波共振分析原理，对典型附加机匣齿轮系统各齿轮进行行波共振分析，由于篇幅所限，本文以1004号齿轮和1007号齿轮为例，给出共振Campbell图，如图15、16所示。

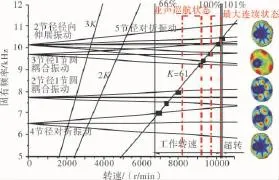
图1　51004号齿轮共振Campbell

从图15中可见，在工作转速范围内，1004号齿轮有5阶共振模态，分别对应轮体4节径对折振动、轮体2节径与1节圆耦合振动、轮体3节径与1节圆耦合振动、轮体2节径轮体径向伸展振动和轮体5节径对折振动。根据2.2节的分析可知，仅轮体主导的2节径径向伸展振动可被激起。

从图16中可见，在工作转速区间范围内，1007号齿轮有2阶共振模态，分别为轮体3节径对折振动和轮体1节径径向伸展振动，仅轮体1节径径向伸展振动可被激起。

由行波共振分析可知，由于航空发动机工况转速十分广泛，因此共振产生可能性很大，严格来讲，不可能完全避免共振。但是共振实为能量聚集过程［14］，只要齿轮共振转速不落在常用工作转速下，或者在共振转速停留较长时间，则共振破坏可能性较小，可以达到使用要求。

为了判断各齿轮是否发生共振破坏，需要确定常用工作转速区间。根据文献［15］给出发动机2个常用工作转速区间：

（1）在亚声巡航状态下，工作转速区间n=（80%～90%）nmax；

（2）在最大连续状态下，工作转速区间n=（95%～100%）nmax。

将2个常用转速区间在行波共振分析图中标出，如图15、16中的红色方框所示。从图中可见，1004号齿轮可被激起的2节径径向伸展振动不落在该区间，因此可达到使用要求，为非危险齿轮；1节径径向伸展振动落在常用工作转速区间内，因此可能发生共振破坏，将其确定为危险齿轮。

同理，对附件机匣其他齿轮进行分析，最终确定危险齿轮为1003、1006和1007号齿轮。

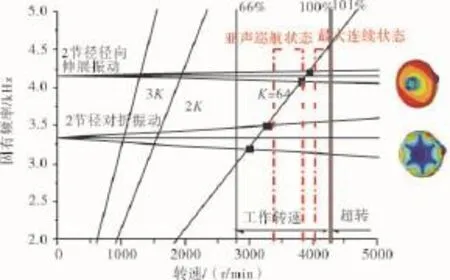
图16　1007号齿轮共振Campbell

3　基于齿轮系统共振分析的危险齿轮确定

3.1齿轮系统等效有限元模型

根据第1.3节所述，轮齿啮合的存在使得齿轮系统单齿轮主导振动模态固有频率发生变化，且存在耦合振型，导致单齿轮共振分析存在一定误差，因此通过建立齿轮系统的有限元模型进行共振分析，从而对单齿轮共振分析确定的危险齿轮进行修正补充。

3.农村新型养老保险。国务院从2009年起开展新型农村社会养老保险(简称新农保)试点。新型农村社会养老保险是以保障农村居民年老时的基本生活为目的，由政府组织实施的一项社会养老保险制度，是国家社会保险体系的重要组成部分。养老待遇由社会统筹与个人账户相结合，与家庭养老、土地保障、社会救助等其他社会保障政策措施相配套，建立个人缴费、集体补助、政府补贴相结合的筹资模式。

齿轮系统建模的主要思想是通过对啮合刚度进行模拟从而建立等效有限元模型，本文在文献［16］等效建模方法的基础上，采用弹簧单元模拟啮合刚度，并用质量单元模拟轮齿结构，从而有效减小忽略轮齿带来的误差。实际计算分析表明，这种方法具有通用性好、误差小的优点。

根据GB/T 3480—1997［17］计算得到齿轮啮合刚度，通过UG软件提取得到轮齿质量。基于该方法建立齿轮系统等效有限元模型如图17（a）所示，由于齿轮系统结构较大，因此分段进行表示如图17（b）所示。

图17　齿轮系统等效有限元模型

轮体和齿轮轴采用实体单元类型为8节点六面体单元Solid185，单元数为108206，轮齿对应质量单元的单元类型为MASS21，单元数为535，啮合刚度采用弹簧单元模拟，单元类型为Combin21，单元数为47，系统总节点数为159245。边界条件的施加与单齿轮的相同，在对应支承处施加相应的径向和轴向约束。

3.2齿轮系统模态振型特性

在ANSYS中对齿轮系统等效有限元模型进行模态计算，提取模态振型。根据各阶振型特点将齿轮系统模态振型分为上、下分支振动，分别包括轮体主导的轴向节径振动（如图18所示）、轮体主导的轴向节圆振动（如图19所示）、轮体主导的径向伸展振动（如图20所示）、齿轮轴主导的周波振动（如图21所示）和齿轮轴主导的径向伸展振动（如图22所示）、耦合振动（如图23所示）。由于提取阶次的原因，没有列出全部振型，高阶模态不在工作转速范围内，因此无需全部进行考虑。

图18　轮体轴向节径振动

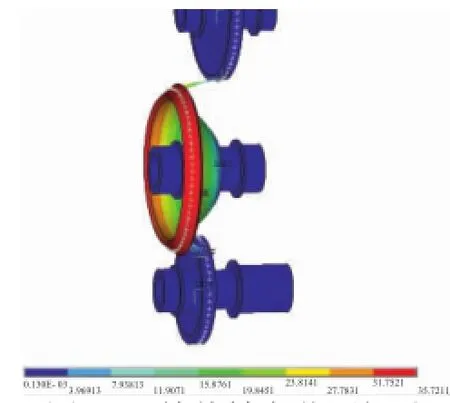
图19　轮体轴向节圆振动

图20　轮体径向伸展振动

图21　齿轮轴周波振动

图22　齿轮轴径向伸展振动

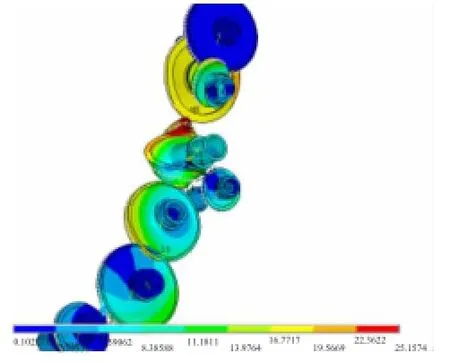
图23　齿轮轴耦合振动

根据齿轮系统激励特性研究上述各类模态是否能被激起。由1.2节分析可知，上、下分支对应的啮合激励频率区间不同，因此当激励频率区间和振动发生位置为不同分支齿轮时，这类振动不会被激起，而激励频率区间和振动位置为同一分支时，可分为3方面进行讨论：

（1）当振动为轮体轴向振动时，由于此时附件机匣齿轮系统不存在轴向激励力，不会被激起；

（3）当振动为齿轮轴主导振动（包括齿轮轴扭转振动和周波振动）时，这类情况与2.2节分析相同，仅输入输出轴对应套齿端齿轮轴扭转可能被激起，其余均不会被激起。

3.3齿轮系统危险齿轮的确定

3.3.1共振分析确定共振模态

由2.3.2节的分析可知，当常用工作转速区间范围内出现共振模态时，系统可能发生共振破坏。由于齿轮系统模态十分密集，共振分析较为困难，而根据上一节的分析可知，附件机匣可被激起的模态相对较少，因此通过主动挑选工作转速范围内可被激起的模态振型，并绘制成共振转速图，如图24所示，图中转速以1006号齿轮为基准。为了研究各阶模态振动能量分布，给出工作转速内可被激起共振模态应变能分布，如图25所示。

从共振转速图中可见：

图24　齿轮系统共振转速

图25　共振模态应变能分布

（1）小齿频对应激励线在最大连续状态与第1阶模态相交，对应阶次为65；

（2）大齿频对应激励线在亚声速巡航状态和最大连续状态下均有2个共振点，对应的阶次为150、155、177和178。

上述5阶危险共振模态的共振频率和共振转速见表2。

表2　共振频率和共振转速

3.3.2应变能分析确定危险齿轮

由上节的分析可知，齿轮系统在工作转速区间范围内存在5阶危险共振模态，对上述模态进行应变能分析［18］，结果见表3。

表3　危险共振模态应变能分布

分析结果表明：

（1）65阶应变能主要集中在1007号齿轮，150和155阶应变能集中在1006号齿轮，即这3阶对应的危险齿轮与单齿轮分析一致；

（2）177、178阶应变能主要集中在1004号齿轮，而单齿轮分析中1004号齿轮为非危险齿轮，可见轮齿啮合的影响使1004号齿轮频率发生偏移，从而导致在工作转速范围内可能发生共振破坏，也确定为危险齿轮。

上述分析表明：轮齿啮合使得各齿轮发生耦合作用，齿轮系统固有特性更为复杂，导致通过单齿轮共振分析确定危险齿轮对于部分齿轮判断不准确，而通过对齿轮系统共振分析，可以有效弥补单齿轮分析的不足，更为准确得到齿轮系统危险齿轮。

4　结论

（1）齿轮激励特性与振动方向研究对于判断各类模态共振可能性具有指导意义，基于激励分析并结合行波共振分析可以确定各齿轮是否为危险齿轮；

（2）由于耦合作用，仅由单齿轮共振分析确定的危险齿轮对于部分齿轮判断不准确，通过对齿轮系统共振分析，可以有效弥补单齿轮分析的不足，更为准确地得到齿轮系统危险齿轮；

（3）发动机附件机匣结构庞大、复杂性强，系统设计周期较长，通过共振分析确定危险齿轮，减少了非必要的安全齿轮的分析，大幅减少设计时间。

［1］李润方，王建军.齿轮系统动力学［M］.北京：科学出版社，1997：1-10. LI Runfang，WANG Jianjun.Gear system dynamics［M］.Beijing：Science Press，1997：1-10.（in Chinese）

［2］吴勇军.齿轮传动系统动态啮合特性接触有限元分析与应用研究［D］.北京：北京航空航天大学，2012. WU Yongjun.Contact finite element analysis and application study on dynamic meshing characteristics of gear transmission system［D］.Beijing：Beihang University，2012.（in Chinese）

［3］Hanjun Jiang，Yimin Shao.Dynamic analysis of a multi-mesh gear system with mesh stiffness variation［C］//Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference，Portland，Oregon，USA：IDETC/CIE 2013：1-8.

［4］Jian Lin，Robert G.P.Mesh stiffness variation instabilities in two-stage gear systems［J］.Journal of Vibration and Acoustics.2001，124（1）：68-76.

［5］Chung C H J，Steyer G，Abe T，et al.Gear noise reduction through transmission error control and gear blank dynamic tuning［J］.SAE transaction，1990，108（6）：2829-2837.

［6］Steyer G C，Lim T C.System dynamics in quiet gear design［C］//Proceeding of the 9th International Modal Analysis Conference.Florence，Italy：SEM Society for Experimental Mechanics Inc，1991：999-1005.

［7］宋乐民.发动机中央传动锥齿轮失效机理的试验研究［M］.北京：国防工业出版社，2002：188-201．SONG Lemin.Experimental study of failure mechanism for main drive bevel gear of engine［M］.Beijing：National Defense Industry Press，2002：188-201.（in Chinese）

［8］杨荣，常春江，魏文山，等．某型发动机附件机匣中心传动从动锥齿轮断裂故障分析［J］.航空发动机，1999，25（4）：31-38. YANG Rong，CHANG Chunjiang，WEI Wenshan，et al.Failure analysis of accessory gearbox’s bevel gear［J］.Aeroengine，1999，25（4）：31-38.（in Chinese）

［9］郭梅，陈聪慧，王建军，等.发动机附件机匣结构系统振动特性［J］.航空动力学报，2013，28（7）：1607-1612. GUO Mei，CHEN Conghui，WANG Jianjun，etal.Vibration characteristics of accessory gearbox structure system of engine［J］. Journal of Aerospace Power，2013，28（7）：1607-1612.（in Chinese）

［10］郭梅，邢彬，史妍妍.航空发动机附件机匣结构设计及齿轮强度分析［J］.航空发动机，2012，38（3）：9-11. GUO Mei，XING Bin，SHI Yanyan.Structural design and strength analysis of accessory gearbox system for aeroengine［J］.Aeroengine，2012，38（3）：9-11.（in Chinese）

［11］李占营.基于有限元法的齿轮系统振动分析及控制［D］.北京：北京航空航天大学，2007. LI Zhanying.Vibration analysis and suppression of gear train system based on finite element method［D］.Beijing：Beihang University，2007.（in Chinese）

［12］张锦，刘晓平.叶轮机振动模态分析理论及数值方法［M］.北京：国防工业出版社，2001：130-150. ZHANG Jin，LIU Xiaoping.Theory and numerical method of turbine vibration modal analysis［M］.Beijing：National Defense Industry Press，2001：130-150.（in Chinese）

［13］晏励堂，朱梓根，李其汉.高速旋转机械振动［M］.北京：国防工业出版社，1994：92-100. YAN Litang，ZHU Zigen，LI Qihan.Vibration of high rotating speed machinery［M］.Beijing：National Defense Industry Press，1994：92-100.（in Chinese）

［14］晏励堂，朱梓根，李其汉，等.结构系统动力特性分析［M］.北京：北京航空航天大学出版社，1989：70-78. YAN Litang，ZHU Zigen，LI Qihan，et al.Analysis of the dynamic characteristics of structure system［M］.Beijing：Beihang University Press，1989：70-78.（in chinese）

［15］廉莜纯，吴虎.航空发动机原理［M］.西安：西北工业大学出版社，2005：274-280. LIAN Youchun，WU Hu.Aeroengine principle［M］.Xi’an：Northwestern Polytechnical University Press，2005：274-280.（in chinese）

［16］阚川.齿轮结构参数振动仿真和行星齿轮系统振动分析［D］.北京：北京航空航天大学，2007. KAN Chuan.Simulation of parametric vibration of gear pair and vibration analysis of planetary gear system［D］.Beijing：Beihang University，2007.（in chinese）

［17］机械工业部郑州机械研究所.GB/T 3480—1997渐开线圆柱齿轮承载能力计算方法［S］.北京：中国标准出版社，29-31. Zhenzhou Research Institute of Mechanical Engineering.GB/T 3480—1997 Methods for the calculation of load capacity of involute cylindrical gears［S］.Beijing：China Stander Press，29-31.（in Chinese）

［18］葛长闯.谐调与失谐两级叶盘结构振动特性研究［D］.北京：北京航空航天大学，2009. GE Changchuang.Research on vibration characteristics about tuned and mistuned two-stage blade disk structure［D］.Beijing：Beihang University，2009.（in Chinese）

（编辑：赵明菁）

Determine the Dangerous Gear in Accessory Gear System of Engine Based on Resonance Analysis

OUYANG Xu-jing1，GUO Mei2，WANG Jian-jun1
（1.School of Energy and Power Engineering，Beihang University，Beijing 100191，China；2.Key Laboratory for Power Transmission Technology of Aeroengine Shenyang Engine Design and Research Institute，Shenyang 110015，China）

In order to determine the dangerous gears in the accessory gear system of a typical engine，modal characteristics of each gear were calculated，the Campbell plot was drawn by traveling-wave resonance analysis，the number of dangerous gear were preliminary got.The gear system was simulated using equivalent finite element method to study the resonance characteristics of the gear system.New dangerous gears within the working speed were determined based on resonance analysis of the gear system.Dangerous gears were determined through strain energy method；the results of the single gear analysis were added.The results indicate that the method and technique can determinate dangerous gear of complex accessory gearbox system effectively，reduce the design time，provide reference for test measurement and fault analysis.

dangerous gear；accessory gearbox；resonance analysis；gear system；single gear；aeroengine

V 232.8

A

10.13477/j.cnki.aeroengine.2016.01.006

2015-03-03

欧阳旭靖（1989），男，在读硕士研究生，研究方向为发动机强度、振动与可靠性；E-mail：oyxj1989@163.com。

引用格式：欧阳旭靖，郭梅，王建军.基于共振分析的发动机附件传动系统危险齿轮的确定［J］.航空发动机，2016，42（1）：25-31.OUYANG Xujing，GUO Mei，WANG Jianjun.Determine the dangerous gear in accessory gear system of engine based on resonance analysis［J］.Aeroengine，2016，42（1）：25-31.