90°多弯管阻力系数计算方法

成锋娜，常海萍，田兴江，张镜洋，陆海鹰

（1，2.南京航空航天大学能源与动力学院1，航天学院2，南京210016；3.中航工业沈阳发动机设计研究所，沈阳110015）

90°多弯管阻力系数计算方法

成锋娜1，常海萍1，田兴江1，张镜洋2，陆海鹰3

（1，2.南京航空航天大学能源与动力学院1，航天学院2，南京210016；3.中航工业沈阳发动机设计研究所，沈阳110015）

为准确获得90°组合多弯管阻力系数，采用数值模拟方法对S弯管管内流动进行模拟，并通过分析归纳S弯管局部阻力的相邻影响机制及规律，提出了90°组合弯管阻力系数计算方法。研究结果表明：弯管阻力系数受2弯连接段长度影响的规律与文献试验结果一致，数值计算方法准确有效；当连接段长度大于4倍管径时，S弯管阻力系数呈线性增长；提出的90°组合弯管阻力系数计算方法考虑了多弯管间相邻影响，且采用提出的方法计算了3弯管和多弯管的阻力系数，并将结果与数值模拟结果进行了对比，二者之间的差距均在3%之内，适合工程应用。

90°组合弯管；数值模拟；阻力系数；管内流动

0　引言

弯管管内流动是1种基本的现象，在发动机系统、暖气装置、通风设备、煤气和天然气输送、热电厂及核电冷却水循环系统等工业设备中有广泛存在。

对于单个弯头或弯管的水力特性，国内外许国学者曾进行过研究［1-13］。最早且深入细致研究者首推前苏联学者依杰里奇克［1］，其研究结果表明，水流流经弯头时，由于受离心惯性力的作用，外侧壁压力升高，内侧壁压力降低；外侧壁处的流速相应较小，内侧壁处的流速则较大；弯头的阻力系数不仅与雷诺数有关，而且与弯头的几何参数（如弯角、曲率半径、进出口面积比等）有关。阻力系数是管道设计中极为重要的水力参数，掌握其规律有助于提高设计的合理性。已发表文献主要研究单个和S型或者U型弯管阻力系数，缺乏对多个组合弯管阻力系数的研究。另外，在文献［1］中给出一些几何参数确定的组合弯管阻力系数的计算方法，但是对于任意组合弯管的阻力系数并未提出具体实用的计算方法。

本文通过对组合弯管进行数值模拟，认识相邻弯管间局部阻力影响的机制，期望得到适用于工程应用的组合弯管阻力系数计算方法。

1　物理模型和数值计算方法

1.1计算模型

计算模型为标准的维弯曲管道，弯管的横截面直径D=50 mm。本文所研究弯管的模型简图见表1；对其流动特性进行数值分析时所采用的参数及范围表2。2个U型弯相组合必然会干涉，但在此不进行讨论。

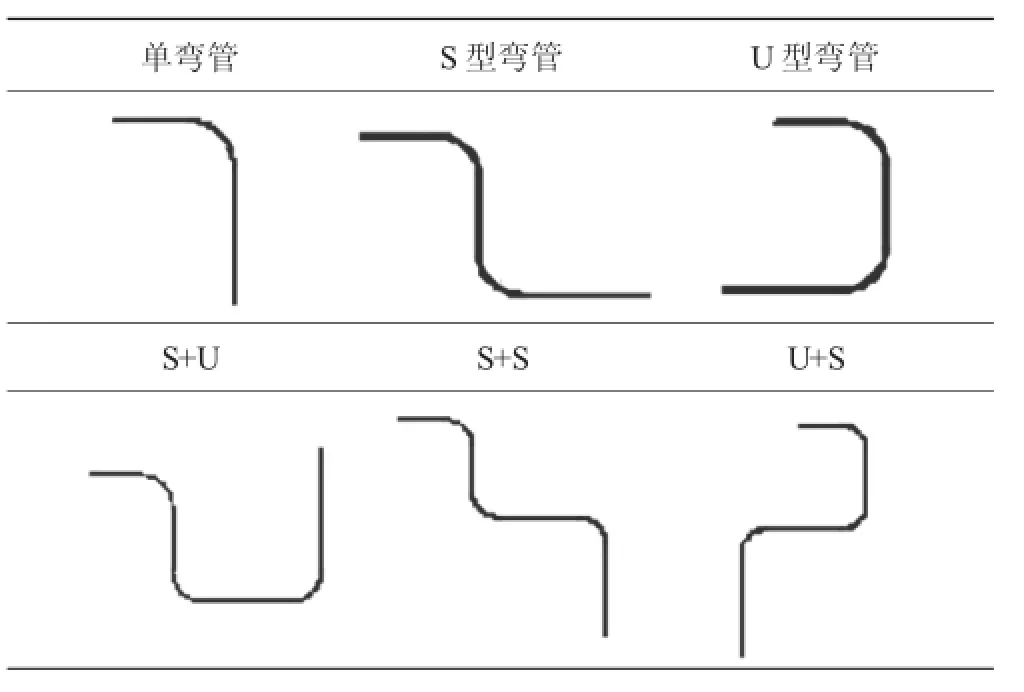
表1　计算模型

表2　计算参数

1.2网格划分

本文采用ICEM软件对计算模型进行网格划分。在近壁处加密使计算表面的Y+≈3以满足加强壁面处理要求。所有计算通过网格独立性试验，单弯管网格数选为70万。

1.3计算方法及边界条件

在文献［14］中把计算结果与文献［15］中的试验的结果进行了对比，验证了计算方法的正确性，本文在此基础上开展数值研究。计算模型进口为速度进口，采用UDF编程将进口设置为充分发展湍流，Re=2× 105；出口为压力出口，压力为环境压力。

2　计算结果及分析

2.12弯局部阻力的相邻影响

组合弯管相邻弯之间的间距小于其间影响长度，弯管间就会产生局部阻力的相邻影响，因此，组合弯管的阻力系数一般不等于弯管独立时的阻力系数之和。充分认识组合弯管中相邻弯之间的影响机制是确定组合弯管阻力特性的前提。

图1　R/D=1的90°单弯管速度及流线分布

R/D=1的90°单弯管速度及流线分布如图1所示。从图中可见，相对直管进口处是呈对称分布的速度型面，在离心力的作用下弯管内产生强烈的二次流，会一直沿着直管段发展，持续很长的距离。不同连接段长度下S型弯管速度分布及流线如图2所示。从图中可见，不同连接段长度下第1个弯前后的流速分布特征和单弯管的基本相同，然而其产生的二次流发展长度会随着连接段长度的改变而变化，因此压力损失也与单弯管的有所不同。

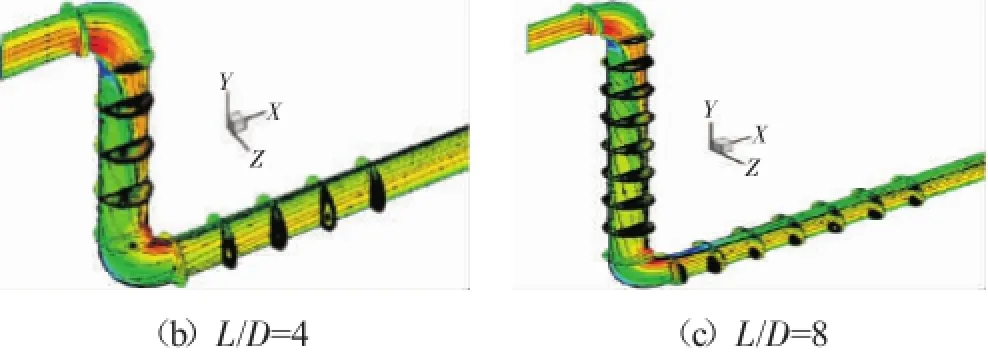
图2　R/D=1，L/D=0、4、8的90°S型弯管速度及流线

R/D=1的90°S型弯管不同连接段长度下第2个弯进出口截面速度分布及流线如图3所示。结合图2可见，不同连接段长度对第2个弯的流动状态影响较大：L/D=0时，第2个弯的进口有在第1个弯产生的二次流，其强度较大，且流体的高速部分由于惯性沿着内侧壁流过第2个弯；第2个弯的出口存在流速较高的惯性区，在其作用下第1个弯的二次流的涡系被挤压到管子下部，且在第2个弯的离心力作用下二次流被衰减。L/D=4时，第2个弯的进口仍有在第1个弯产生的环流，但环流的强度随着连接段长度增加而减弱；第2个弯出口仍存在较高流速的惯性区，二次流的涡系仍被挤压到管子下部，但在第2个弯的离心力作用下大为衰减。L/D=8时，在第1个弯产生的二次流在第2个弯的进口处基本平顺，但未完全消失；在离心力的作用下直至第2个弯的出口处才几乎衰减消失，但在第2个弯产生了强度较大的二次流，二者的流动方向相反。

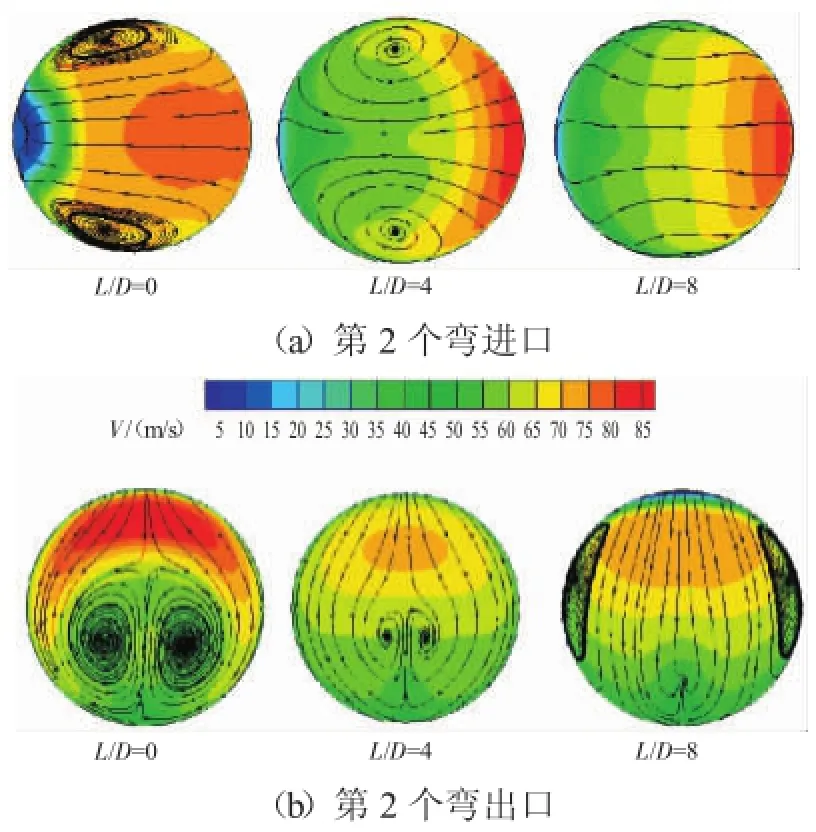
图3　R/D=1，L/D=0、4、8的90°S型弯管第2个弯进、出口截面速度分布及流线

90°S型弯管阻力系数随连接段长度的变化曲线如图4所示。从图中可见，在不同的相对曲率半径下，当L/D≥4后阻力系数均呈线性增长。

2.2组合弯局部阻力的相邻影响

图4　90°S型弯管阻力系数随连接段长度变化曲线

多弯组合相邻弯局部阻力影响机制与2弯一致，故可认为L/D≥4以上的相邻弯管之间的影响是有规律可循的。R/D=1，L/D=6的90°的多种弯管速度分布如图5所示。从图中可见多弯组合弯管第1个弯的流动状况和单弯管的相似，第2个弯之后的各弯流动状态基本相同，反映出该弯的阻力系数只与前弯和连接段长度有关。

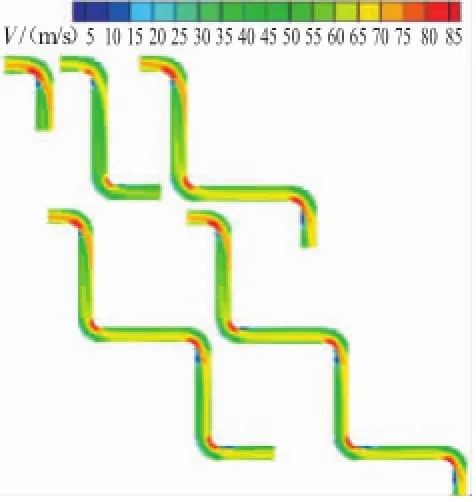
图5　R/D=1，L/D=6的90°弯管速度分布

2.3阻力系数的计算对比与分析

数值计算得到的S型弯管阻力系数和文献［1］中的阻力系数对比如图6所示。从图中可见，二者之间吻合很好，特别是L/D≥4以上二者的差距基本在5%之内，证明了数值计算的准确性。

图6　R/D=1的90°S型弯管阻力系数随连接段长度变化

2.490°组合弯管阻力系数计算方法

通过对多弯管的阻力特性分析，本文提出了相对连接段长度L/D≥4，相对曲率半径1≤R/D≤3的90°组合弯管阻力系数计算方法，具体如下：

式中：ζ为总阻力系数；ζMi为第i弯管的单弯管局部阻力系数，可采用文献［1］中的局部阻力试验结果；为第i弯管弯曲部分的摩擦阻力系数为连接段长度的摩擦阻力系数；Ai为第i弯的局部阻力系数的修正系数。

计算中需要确定的值只有局部阻力系数的修正系数Ai值。本文认为第2个弯以后的局部阻力系数只与前弯和连接段长度有关，则引入下列几条修正系数取值原则：

（1）当连接段长度L/D＞25时，截断弯管，将下一个弯管的局部阻力作为第1个弯重新开始计算。

（2）第1个弯的局部阻力系数修正系数Ai与相对曲率半径有关。R/D=1时，A1-0.6AS/U；R/D=2时，A1=0.7AS/U：R/D≥2.5时，A1=0.5AS/U。

其中AS/U为由第1个弯和第2个弯组成的S/U型弯管在文献［1］中的局部阻力系数修正系数，其值是L/D的函数。

（3）第2个弯及其后面的弯管局部阻力系数的修正系数Ai值如下。R/D=1时，Ai=0.4AS/U；R/D=2时，A1=0.3AS/U：R/D≥2.5时，A1=0.5AS/U。

其中AS/U为本弯及其前弯组成的S/U型弯管在文献［1］中的局部阻力系数修正系数。若2弯的相对曲率半径不同，按照本弯的相对曲率半径计算。

数值计算的3弯管阻力系数和采用本文提出的公式值之间的对比如图7所示。从图中可见，二者非常接近，误差均在3%之内。

2.5算例验证

某一平面90°组合多弯管如图8所示，其中转弯的方向、相对曲率半径以及连接段长度都在计算方法所适用的参数范围内任意选取，组合弯管具有9个弯和8个连接段，为了直观仅显示其轴线。从左端入口到出口分别为第1，2…i…9弯，弯头编号与相对曲率半径的对应关系见表3。

图7　90°3弯管阻力系数随第2个连接段长度变化

图8　任意组合多弯管

表3　多弯管弯头相对曲率半径

第1、2个弯之间直管段定义为第1个连接段长度，则从左端入口到出口分别为第1，2…j…8个连接段，连接段编号与相对连接段对应关系见表4。

表4　多弯管弯头连接段

计算进口采用UDF编程设置为充分发展湍流，Re=2×105；出口为环境压力。

采用本文提出的方法对阻力系数进行计算

采用数值计算方法得到多弯管阻力系数值为2.50，二者之间相差在3%之内，证明本文提出的方法精确可靠。

3　结论

组合弯管相邻弯之间的间距小于其间影响长度时，弯管间就会产生局部阻力的相邻影响；当L/D≥4以上的相邻弯管之间的影响是随着L/D的增长呈线性增长的；采用本文提出的方法计算了3弯管和多弯管的阻力系数，并将结果与数值模拟结果进行了对比，二者之间的差距均在3%之内，证明了本文提出的计算方法可靠，适用于工程应用。

［1］Idelichik.Handbook of hydraulic resistance（3rd edition）［M］.New York：Jaico Publishing House，2008：331-409.

［2］尚虹，王尚锦，席光，等.90°圆截面弯管内三维紊流场实验研究［J］.航空动力学报，1994，9（3）：263-266. SHANG Hong，WANG Shangjin，XI Guang，et al.Experimental study of three-dimensional turbulent flow field within 90°bend of circular cross section［J］.Journal of Aerospace Power，1994，9（3）：263-266.（in Chinese）

［3］潘忠兴，侯成仁，闰芳.90°弯管内湍流流动的数值模拟［J］.化学工业与工程技术，2011，32（1）：4-7. PAN Zhongxing，HOU Chengren，RUN Fang.Numerical simulation study of turbulent flow field in 90°bend pipe［J］.Journal of Chemical Industry and Engineering，2011，32（1）：4-7.（in Chinese）

［4］江山，张京伟.基于FLUENT的90°圆形弯管内部流场分析［J］.中国舰船研究，2008，3（1）：37-41. JIANG Shan，ZHANG Jingwei.Numerical simulation of inner flow in 90°bending duct of circular-section based on FLUENT［J］.Chinese Journal of Ship Research，2008，3（1）：37-41.（in Chinese）

［5］李盛元，刘宁宁，李勇.流体流经垂直弯管时内部流场的数值模拟［J］.东北电力大学学报，2009，29（1）：67-70. LI Shengyuan，LIU Ningning，LI Yong.Numerical simulation on flow field of 90°elbow pipe［J］.Journal of Northeast China Institute of Electric Power Engineering，2009，29（1）：67-70.（in Chinese）

［6］湛含辉，朱辉，陈津端，等.90°弯管内二次流（迪恩涡）的数值模拟［J］.锅炉技术，2010，41（1）：1-5. ZHAN Hanhui，ZHU Hui，CHEN Jinduan，et al.Numerical simulation of secondary flow（dean vortices）in 90°curved tube［J］.Boiler Technology，2010，41（4）：1-5.（in Chinese）

［7］杨任.方形弯管内部流动与阻力系数的数值计算［J］.管道技术和设备，2008（5）：30-33. YANG Ren.Numerical computations of the flow and hydraulic loss coefficient in a 90°bend with a square-cross-section［J］.Pipeline Technique and Equipment，2008（5）：30-33.（in Chinese）

［8］贺益英，赵懿珺，孙淑卿，等.输水管线中弯管局部阻力的相邻影响［J］.水利学报，2003（11）：54-58. HE Yiying，ZHAO Yijun，SUN Shuqing，et al.Interaction of local loss between bends in pipe line［J］.Journal of Hydraulic Engineering，2003（11）：54-58.（in Chinese）

［9］苏沛兰，董志勇，姚科云，等.S型与U型管道阻力规律对比研究［J］.山西农业大学学报，2004，24（4）：392-395 SU Peilan，DONG Zhiyong，YAO Keyun，et al.A comparison of resistance characteristics between U-like and S-like pipes［J］.Journal of Shanxi Agricultural University，2004，24（4）：392-395.（in Chinese）

［10］赵懿珺，贺益英.直角Z形组合双弯管流动特性的研究［J］.水利学报，2006，37（7）：778-783. ZHAO Yijun，HE Yiying.Hydraulic characteristics of Z-type pipecombination with two similar rectangular bends［J］.Journal of Hydraulic Engineering，2006，37（7）：778-783.（in Chinese）

［11］Crawford N M，Cunningham G，Spedding P L.Prediction of pressure drop for turbulent fluid flow in 90°bends［J］.Proceedings of the Institution of Mechanical Engineers，2003，217：153-155.

［12］Crawford N M，Cunningham G，Spence S W T.An experimental investigation into the pressure drop for turbulent flow in 90°elbow bends［J］.Proceedings of the Institution of Mechanical Engineers，2007，221：77-88.

［13］Crawford N M，Spence S，Simpson A，et al.A numerical investigation of the flow structures and losses for turbulent flow in 90°elbow bends［J］.Proceedings of the Institution of Mechanical Engineers， 2009，223：27-44.

［14］成锋娜，常海萍，田兴江，等.小转角小曲率半径弯管阻力系数研究［C］//第7届江苏省工程热物理学会论文集.扬州：2013：428-433. CHENG Fengna，CHANG Haiping，TIAN Xingjiang，et al.Resistance coefficient of bend with small corner and small radius［C］//Proceedings of the Seventh Academic Conference of Jiangsu Province Society of Engineering Thermo Physics.Yangzhou：2013：428-433.（in Chinese）

［15］Pruvost J，Legrand J，Legentilhomme P.Numerical investigation of bend and tours flows，part I：effect of swirl motion on flow structure in U bend［J］.Chemical Engineering Science，2004，59（16）：3345-3357.

（编辑：栗枢）

Calculation Method of Resistance Coefficient in 90°Combined Bends

CHENG Feng-na1，CHANG Hai-ping1，TIAN Xing-jiang1，ZHANG Jing-yang2，LU Hai-ying3
（1，2.College of Energy and Power Engineering，College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 2100016，China；3.AVIC Shenyang Engine Design and Research Institute，Shenyang 110015，China）

In order to gain accurate resistance coefficients，a calculation method of 90°combined bends was proposed by investigating on flow of S-like bends with numerical simulation method，analysing and summarizing local resistance adjacent impact mechanism and law.The results show that the numerical simulation method of bends is precise and efficient due to a good agreement between the impact on resistance coefficient by the length of 2 bends and experimental data of published papers.The local resistance coefficient of S-like bends increase linearly when the connection section is 4 times longer than bends'diameter.Considering adjacent impact of bends，the resistance coefficient on triple bends and multiple bends are calculated.The difference between the calculation method of 90°combined bends and numerical simulation，which is suitable for engineering use，is less than 3 percent.

90°combined bends；numerical simulation；resistance coefficient；interior flow

V 231.1

A

10.13477/j.cnki.aeroengine.2016.01.002

2015-06-22基金项目：国家自然科学基金（51406085）、江苏省研究生培养创新工程（KYLX_0306）、中央高校基本科研业务费专项资金资助

成锋娜（1988），女，在读博士研究生，研究方向为涡轮叶片冷却；E-mail：cfn1218@163.com。

引用格式：成锋娜，常海萍，田兴江，等.90°多弯管阻力系数计算方法［J］.航空发动机，2016，42（1）：6-10.CHENG Fengna，TIAN Xingjiang，CHANG Haiping，et al.Analysis of resistance characteristics in 90°combined bends［J］.Aeroengine，2016，42（1）：6-10.