涡轴发动机双回路PI控制器多发功率匹配
2016-10-27时瑞军周剑波高世煌
杨 超,王 曦,时瑞军,周剑波,高世煌
(1.北京航空航天大学能源与动力工程学院,北京100191;2.先进航空发动机协同创新中心,北京100191;3.中航工业航空动力机械研究所,湖南株洲412002)
涡轴发动机双回路PI控制器多发功率匹配
杨超1,2,王曦1,2,时瑞军3,周剑波3,高世煌3
(1.北京航空航天大学能源与动力工程学院,北京100191;2.先进航空发动机协同创新中心,北京100191;3.中航工业航空动力机械研究所,湖南株洲412002)
为了应对多个发动机共同驱动同一直升机时,单个发动机性能衰退所引发的输出功率不平衡问题,以控制2个转子转速的双回路结构PI控制器为基础,将外回路改为直接功率控制回路,搭配能够计算旋翼在一定转速下需求功率的机载模型,构建了1种涡轴发动机多发功率平衡匹配控制系统。内回路分别采用燃气发生器转子转速控制回路和动力涡轮转子转速控制回路,得到参数不同的控制器并进行了仿真验证和对比。结果表明:所设计的双回路PI控制器能够在保证涡轴发动机动力涡轮转速恒定的同时,使性能衰退程度不同的2台发动机输出相同的功率。
PI控制器;涡轴发动机;双回路结构直接功率控制;功率平衡匹配控制
0 引言
涡轴发动机自20世纪50年代以来一直作为直升机的主要动力装置[1]。由于直升机的特殊性,涡轴发动机的工作状态与直升机旋翼等负载系统的工作状态相互影响,所以在直升机的工作过程中,一般都要求保持旋翼的转速恒定[2-3]。于是,涡轴发动机控制系统在保证发动机自身受到干扰时可以稳定工作并且响应快速外,都要控制动力涡轮转速在工作时保持恒定[4-7]。
传统的涡轴发动机控制采用串级双回路控制器。内回路以燃气涡轮发生器转子转速为控制量,使发动机快速响应外界变化;外回路以动力涡轮转子转速为控制信号,保证在任何工作状态下转速保持恒定。采用基于LMI(线性矩阵不等式)设计鲁棒PI控制器的方法求取控制器参数,根据相应的结论建立线性矩阵不等式约束,可以通过软件求解得到满足要求的控制器参数[8-11]。基于PI控制器的参数算法已在国内外得到广泛的应用并且十分成熟[12-14]。
即使是同一个型号的发动机,由于制造误差及使用中不同程度的性能退化,每个发动机的性能也并不完全相同,因此,在双发乃至多发共同驱动同一直升机的情况下,上述控制系统无法保证每个发动机在同一时刻输出的功率相同,这使得直升机的操纵变得不稳定[15-17]。
为改善上述情况,本文参考基于模型的性能退化缓解智能PDMIC(Performance Deterioration Mitigation Intelligent Control)技术[16-17],在传统双回路转速控制器的基础上设计基于模型的涡轴发动机双回路直接功率控制器,在发动机性能退化时,保证双发输出相同的功率和动力涡轮转速。
1 单一发动机直接功率控制系统原理及结构
要实现基于模型的性能退化缓解智能控制,需要对发动机双回路结构控制系统(如图1所示)进行改进。
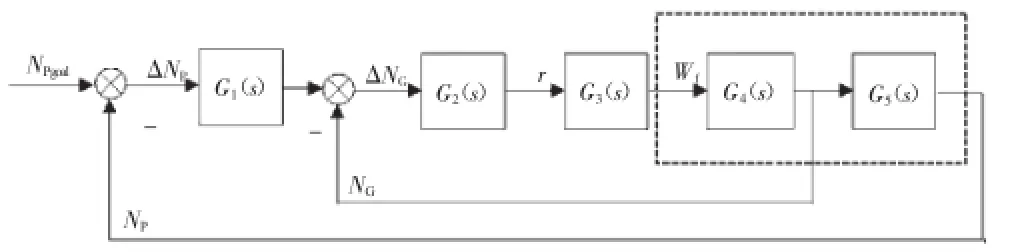
图1 双回路结构PI控制器结构
图中不同下标的G(s)代表不同部件或者系统模块的传递函数。虚线框内为发动机某些物理量间的传递函数,G4(s)为燃油流量Wf到燃气发生器转子转速NG的传递函数,G5(s)为燃气发生器转子转速NG到动力涡轮转子转速NP的传递函数。G3(s)为燃油调节器执行机构的传递函数,即控制器计算出的指令r到燃油流量Wf的传递函数。G2(s)为内回路NG控制器,G1(s)为外回路NP控制器,在考虑使用PI控制器时,传递函数可表示为

在设计控制系统前,需要获得虚线框内发动机的传递函数,依据发动机的部件特性以及气动热力学和转子动力学方程建立发动机部件级非线性模型。在此基础上将其线性化,得到发动机的线性模型[4-5],最终从线性模型中得到这些传递函数。执行机构的传递函数因机构类型不同而略有差别,将其假设为1个1阶惯性环节,结构控制器(图1)可以达到单个涡轴发动机的控制要求。有关串级双回路转速PI控制器的详细设计过程以及参数见文献[8]。
在如图1所示的原控制系统中,外回路控制器G1(s)输入的控制信号为动力涡轮转子目标转速(一般为设计值),但考虑到在双发或者多发匹配的涡轴发动机控制系统中,直升机在稳定工作的同时需要保证各发动机动力涡轮轴输出的功率相同,即控制系统需要根据给定的功率信号控制发动机输出目标功率,需要将外回路控制器的控制信号变为发动机动力涡轮轴上的目标输出功率。与此同时,为保证在任意工况下,直升机发动机的旋翼转速都能保持稳定,需要1个机载模型准确计算出驾驶员总距角(旋翼桨距角)与转速在设计值时旋翼等负载系统需求功率的对应关系。在计算机仿真中,仅需使用旋翼模型即可实现这一要求。用旋翼模型中的特性数据计算出在设计旋翼转速时桨距角与需求功率的关系,根据驾驶员输入的桨距角将对应的需求功率作为外回路的控制信号输入控制器,便可实现在保证旋翼稳定工作的前提下对动力涡轮轴输出功率的直接控制。此时,内回路控制器保持不变,以燃气发生器转子转速为控制信号,外回路中的反馈信号由如图1所示的动力涡轮转子转速信号变为动力涡轮轴的输出功率信号,在发动机输出功率(PPT)值无法直接通过传感器测量的情况下,该物理量可以使用扭矩传感器测量,动力涡轮轴输出扭矩(PQT)与转速传感器测量出的动力涡轮转子转速(NP)通过式(1)计算得出,整个控制系统的控制结构如图2所示。

式中:PPT为发动机输出功率,kW;PQT为动力涡轮轴输出扭矩,N·m;NP为动力涡轮转子转速,r/min。

图2 单个发动机直接功率控制器结构
根据如图2所示的控制系统结构以及如图1所示的双回路结构PI控制器传递函数结构,由发动机模型及旋翼模型得到需要的传递函数,先求取内回路控制器的参数,将内回路控制器以及控制对象等效为广义的控制对象,再运用控制器参数计算的相应结论求解出外回路控制器的参数;然后运用基于LMI的鲁棒PI控制器参数整定算法,求出满足控制系统性能要求的单个发动机PI控制器参数。控制器设计的详细方法及原理见文献[8-11]。
2 双(多)发功率平衡控制的实现
实现对单个发动机的直接功率控制后,便可考虑多个发动机共同驱动同一直升机时控制平衡分配。基于前文对控制器的改进,可以根据输入的需求功率实现对动力涡轮轴输出功率的伺服跟踪,采用机载旋翼模型计算出准确的旋翼(负载)需求功率并平均分配给各发动机即可。以2个发动机平衡匹配为例,功率匹配结构如图3所示。图3中的发动机控制器原理以及结构与图2中的相同。从图中可见,只要求得满足要求的单个发动机直接功率控制系统中PI控制器的参数,即可实现这种控制结构。

图3 双发功率平衡控制系统结构
3 仿真验证
依据前述的控制系统原理以及结构,可以建立对应的模型进行仿真,最终验证方案的可行性。本文采用Matalb软件中的Simulink平台进行仿真验证,非线性模型建模过程中需要的部件特性数据以及气体的热力参数来源于文献[4-5]。由于受部件特性数据适用范围的限制,仿真只能在发动机空中慢车以上的工况下进行,以空中慢车工况作为仿真的最小工况,对应驾驶员总距操纵杆角度假设为0°,最大状态对应总距操纵杆角度为67°。仿真时长为40 s,仿真时,发动机1正常工作,发动机2压气机效率下降3%以模仿发动机性能衰退,仿真时不考虑因发动机性能下降而无法达到的工况。
据文献[8-12]可以计算出外回路为直接功率控制,内回路为燃气发生器转子转速控制的串级双回路控制系统的控制器参数。直接功率控制回路PI控制器参数Kp1=18.9112,K12=37.1863;燃气发生器转子转速控制回路PI控制器参数Kp2=1.2683×10-5,K12= 2.0683×10-5。
总距杆角度从最大角度的80%加大到90%,控制器与发动机组成闭环系统的调节响应如图4~8所示,总距杆变化过程持续1 s。总距杆角度的变化如图4所示。
燃油流量随时间的响应过程如图5所示。从图中可见,因性能退化,发动机2需要消耗更多的燃油才能达到与发动机1相同的输出功率。

图4 驾驶员总距杆输入角度

图5 燃油流量响应
燃气发生器和动力涡轮的转子转速的调节情况分别如图6、7所示。从图中可见,燃气发生器转子转速调节较快,动力涡轮转子转速动态响应过程稍长,但进入稳态后转速稳定。在进入稳定状态后,根据不同发动机的部件特性以及整机匹配性能,在工作环境相同且输出功率相同的条件下,压气机性能衰退后,燃气发生器转子转速可能高也可能低,需要性能良好的控制系统给予正确的调节,而性能退化后的发动机2可以与发动机1保持相同的动力涡轮转子转速并有相似的动态调节过程。
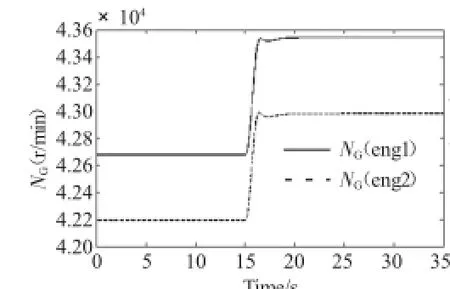
图6 燃气发生器转子转速响应
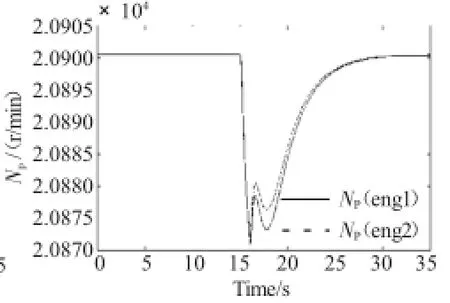
图7 动力涡轮转子转速响应

图8 功率平衡匹配响应
2个发动机动力涡轮轴的输出功率如图8所示。从图中可见,二者在2个工作状态下的输出功率相等,证明如图3所示的带有功率匹配功能的控制系统结构可实现,且可达到预期功能。
4 改善转子转速动态响应的控制系统改进方案
通过以上仿真验证结果可知,对于外回路控制动力涡轮轴输出功率,内回路控制燃气发生器转子转速的双回路控制系统,闭环系统中2个转子转速的动态响应品质均一般,尤其是动力涡轮转子转速的动态响应(如图4、9所示)的斜坡输入下需要7~8 s才能进入稳态,响应速度稍慢。发动机动力涡轮轴上的输出功率与燃气发生器转子的转速呈对应关系,直接控制功率可以实现对燃气发生器转子转速的调节。可将内环的PI控制器的控制量改为控制动力涡轮转子转速,改善其动态调节性能。双回路控制系统的结构不变时(图1),G4(s)为燃油流量Wf到动力涡轮转子转速NP的传递函数。控制参数的计算方法仍参考文献[8-12]。外回路为直接功率控制回路,内回路为动力涡轮转子转速控制回路。直接功率控制回路PI控制器参数Kp1=32.0174,K12=100.074;动力涡轮转子转速控制回路PI控制器参数Kp2=5.1299×10-5,K12= 2.9362×10-5。
将设计出的单个发动机控制器组合成如图3所示的功率平衡匹配控制系统结构,并仿照上文进行仿真验证。总距杆如图4所示,在此条件输入下,各物理量的响应如图9~12所示。
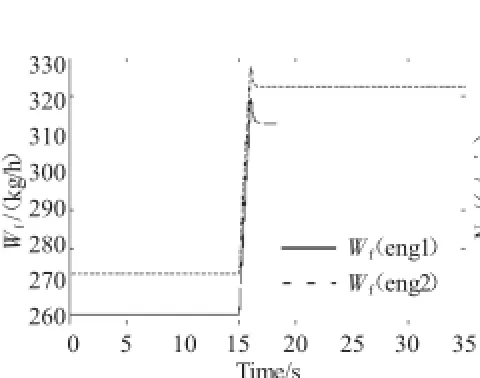
图9 改进控制器的燃油流量响应

图10 改进控制器的燃气发生器转子转速响应
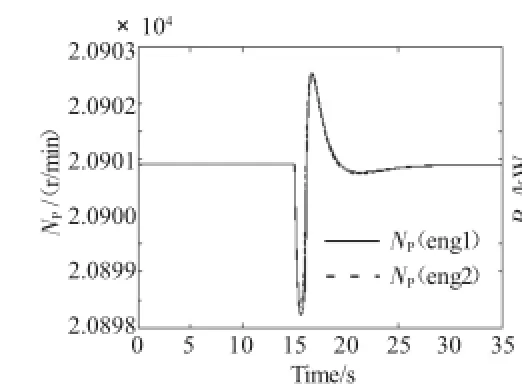
图11 改进控制器的动力涡轮转子转速响应
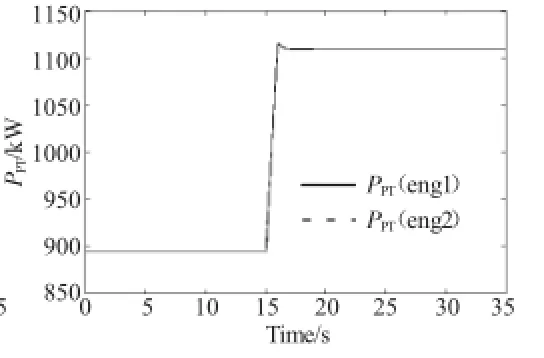
图12 改进控制器的功率平衡匹配
由以上结果可知,改进的双回路控制系统与本文第3章阐述的内回路为燃气发生器转子转速的双回路直接功率控制系统相比具有更好的性能。控制器燃油流量的调节响应(图9)比图5更加灵敏。图11与图7相比,动力涡轮转子在相同斜坡输入时动态响应过程更快,进入稳态的时间在5 s以内,在动态调节过程中,如图7所示的动力涡轮转子转速的最大调节偏差为30 r/min,而如图11所示的控制系统最大调节偏差仅为3 r/min,超调量减小到未改进控制系统的1/10,燃气发生器转子转速的响应速度也相应提高,基本可以与总距杆输入的变化过程保持同步。
综合以上的仿真验证,易知内环为动力涡轮转子转速控制,外环为直接功率控制的双回路结构PI控制器。在实现多发功率平衡匹配功能的同时,还可以保证闭环系统中燃油流量以及转子转速的响应有更好的动态和稳态特性,可视为另1种多发匹配控制系统的设计思路。
5 结论
(1)以某型涡轴发动机为例,以双(多)发共同为同一直升机提供动力时功率平衡匹配为目的,给出了1种基于双回路PI控制器结构的控制系统。将传统的双转速控制模式转换为转速与功率控制模式,将外回路变为直接功率控制回路并加入机载模型计算出旋翼需求功率,以平均分配的方式将信号输入发动机直接功率控制回路中。从给出的仿真验证结果可知,这种控制方式可以在某一发动机性能衰减时实现多发功率平衡匹配。
(2)为了改善动力涡轮转子转速的动态响应,使直升机在整个工作中可以更稳定地工作,将内环控制量改进为动力涡轮转子转速。由仿真结果可见,基于动力涡轮转子输出功率与转速的双回路控制系统不仅可以实现多发功率的平衡匹配,还能使发动机与控制器的闭环系统具有更好的动态调节性能,其转子转速调节过程中的超调量更小,进入稳态的速度更快,同时其他物理量如燃油流量、燃气发生器转子转速的响应特性也能得到改善。对应的仿真验证结果为涡轴发动机多发功率的平衡匹配、涡轮发动机智能控制系统的设计提供了1种思路。
[1]冯海峰.航空涡轴发动机数学建模方法与控制规律研究[D].西安:西北工业大学,2007. FENG Haifeng.Research on modeling method and control stagey foraero-turboshaft[D].Xi’an:Northwestern Polytechnical University,2007.(in Chinese)
[2]张海涛.直升机旋翼/发动机一体化建模研究[D].南京:南京航空航天大学,2009. ZHANG Haitao.Research on rotor/engine integrative modeling for helicopter[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2009.(in Chinese)
[3]时瑞军,周剑波,张秋贵,等.涡轴发动机性能退化数学建模研究[J].航空发动机,2010,36(4):26-28. SHI Ruijun,ZHOU Jianbo,ZHANG Qiugui,et al.Mathematical model study on performance deterioration of turboshaft engine[J].Aeroengine,2010,36(4):26-28.(in Chinese)
[4]Ballin M G.A high fidelity real-time simulation of a small turboshaft engine[R].NASA-TM-100991.
[5]Spack J M.Linear parameter varying controller for a small turboshaft engine[D].Boston:Northeastern University,2011.
[6]Warmbrodt W.Development of a helicopter rotor/propulsion system dynamics analysis[R].AIAA-82-1078.
[7]Mihaloew J R,Ballin M G,Ruttledge D C G.Rotorcraft flight propulsion control integration:an eclectic design concept[R]. NASA-TP-2815.
[8]杨超,王曦.涡轴发动机双回路结构PI控制器设计[J].航空发动机,2014,40(S1):51-56. YANG Chao,WANG Xi.Design of PI controller with double-loop structure for a turboshaft[J].Aeroengine,2014,40(S1):51-56.(in Chinese)
[9]何皑.基于LMI的航空发动机智能容错控制技术研究[D].北京:北京航空航天大学,2011. HE Ai.The LMI-based intelligent fault-tolerant control for aircraft engine[D].Beijing:Beihang University,2011.(in Chinese)
[10]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:96-119. YU Li.Robust control-LMI approach[M].Beijing:Tsinghua University Press,2002:96-119.(in Chinese)
[11]Astrom K J,Hagglund T.PID controllers:theory,design,and tuning[M].The United States:Instrument Society of America,Research Triangle Park,1995:59-200.
[12]ZHENG Feng,WANG Qingguo,LEE Tongheng.On the design of multi-variable PID controllers via LMI approach[J].Optimization Methods and Software,2002(38):517-526.
[13]WANG Xi,SUN Yongxia,ZHENG Tiejun,et al.Static output feedback-base PI control for aeroengines using linear matrix inequality[R].AIAA-2008-4581.
[14]Grant M C,Boyd S P.Matlab software for disciplined convex programming[R/OL].[2013-8-15].http://cvxr.com/cvx/.
[15]Garg S.Controls and health management technologies for intelligent aerospace propulsion systems[R].NASA-TM-2004-212915.
[16]李业波,李秋红,黄向华,等.航空发动机性能退化缓解控制技术[J].航空动力学报,2012,27(4):930-936. LI Yebo,LI Qiuhong,HUANG Xianghua,et al.Performance deterioration mitigation control of aero-engine[J].Journal of Aerosapce Power,2012,27(4):930-936.(in Chinese)
[17]Garg S.NASA Glenn research in controls and diagnostics for intelligent aerospace propulsion systems[R].NASA-TM-2005-214036.
[18]王曦,程茵.国外航空推进控制技术的发展[J].航空发动机,2009,35(3):5-7. WANG Xi,CHENG Yin.Development of thrust control technology for foreign aeroengine[J].Aeroengine,2009,35(3):5-7.(in Chinese)
(编辑:赵明菁)
Power Balance for Multiple Engines Based on Double-Loop PI Controller for Turboshaft
YANG Chao1,2,WANG Xi1,2,SHI Rui-jun3,ZHOU Jian-bo3,GAO Shi-huang3
(1.School of Energy and Power Engineering,Beihang University,Beijing 100191,China;2.Collaborative Innovation Center for Advanced Aero-Engine,Beijing 100191,China;3.AVIC Aviation Power Plant Research Institute,Zhuzhou Hunan 412002,China)
Based on a PI controller with double-loop structure aiming at controlling the speed of two rotor shafts,a control system to balance the power of two or more engines on the same helicopter was achieved with a model which was able to calculate the power demanded by the rotor on a fixed speed to avoid the bad effects of performance degradation of them.The outer-loop was modified to control the power of power turbine shaft,and the inner-loop was designed either to control the speed of gas generator rotor or power turbine rotor. Both controllers were simulated with the same engine model to verify the performance of these kinds of controller.The results show that the controller designed in this paper can keep the power provided by two turboshafts balance at the constant NP when performance degradations of these two engines are different.
PI controller;turboshaft;double-loop structure direct power control;power balance control
V 233.7
A
10.13477/j.cnki.aeroengine.2016.01.004
2014-11-13基金项目:航空科学基金(2011ZB510019)资助
杨超(1989),男,硕士,研究方向为航空发动机控制及故障诊断;E-mail:chtjyc@126.com。
引用格式:杨超,王曦,时瑞军,等.涡轴发动机双回路PI控制器多发功率匹配[J].航空发动机,2016,42(1):16-20.YANG Chao,WANG Xi,SHI Ruijun,et al. Power balance for multiple engines based on double-loop PI controller for turboshaft[J].Aeroengine,2016,42(1):16-20.
