基于EEMD和WT的运动想象脑电信号消噪方法*

蔡　慧，马玉良，佘青山，高云园，孟　明

（杭州电子科技大学智能控制与机器人研究所，杭州310018）

基于EEMD和WT的运动想象脑电信号消噪方法*

蔡慧，马玉良*，佘青山，高云园，孟明

（杭州电子科技大学智能控制与机器人研究所，杭州310018）

采集到的运动想象脑电信号MI EEG（Motor Imagery Electroencephalogram）通常含有大量噪声信号。为了消除噪声同时保留尽可能多的有效信号，本文提出了将集合经验模态分解EEMD（Ensemble Empirical Mode Decomposition）与改进小波阈值法相结合的消噪方法。改进小波阈值法采用了新的阈值选取规则和阈值函数。首先对信号进行EEMD分解，然后再对高频固有模态函数IMF（Intrinsic Mode Functions）进行改进小波阈值处理，最后将处理后的高频IMF分量和低频IMF分量进行重构得到消噪信号。以信噪比和均方根误差作为消噪效果的定量评价指标，将本文提出的方法与单纯使用EEMD分解消噪法、单独使用改进小波阈值消噪法、EMD与改进小波阈值法相结合消噪法进行比较，结果表明，本文提出的消噪法优于其他三种消噪法。

运动想象脑电信号；消噪；EEMD；小波阈值法；IMF分量

EEACC：7230doi：10.3969/j.issn.1004-1699.2016.05.016

运动想象脑电信号近些年常用于脑-机接口系统的研究。由于其显著的非平稳性和非线性，而且信号幅值十分微弱，只有5 μV～150 μV，频率低至几十赫兹以下，极易被眼电，心电，工频干扰，电磁干扰等大量外界干扰信号淹没，这给这类脑-机接口系统的研究带来了很大的挑战［1-3］。因此，有效的信号消噪处理在研究中就显得十分重要。

小波分析［4］因为其多分辨率和良好的时频局域化的特性，所以常用于处理随机信号。而小波阈值法就常用于信号消噪，但是当噪声频率和信号频率较为接近时，常会损失部分有用高频信息，从而导致信号失真。

集合经验模态分解［5］是Wu和Huang在EMD基础上进行改进的。它通过加入白噪声改善信号的极值点分布，能有效的改善EMD的模式混叠现象，大幅提高信号的信噪比。

本文综合上述两种方法的优点，提出了基于EEMD和改进小波阈值法的消噪方法，并将该方法用于运动想象脑电信号处理中，得到了很好的消噪效果，有很高的实用价值。

1　基于EEMD和改进小波阈值法的消噪方法

对于原始运动想象脑电信号，由于幅值较小，单纯利用小波阈值消噪会在压制大部分噪声的同时去除部分小幅度的有效信号，而单纯通过直接去除EEMD分解中的前几个高频IMF分量来消噪时，又会在去掉高频中的噪声成分的同时去除了高频中的有效信息成分［6］。针对这一情况，本文提出了将EEMD和改进小波阈值法相结合，通过双方互补的形式达到更有效的消噪效果。

1.1集合经验模态分解

EEMD主要利用了白噪声的频率均匀分布的统计特性来解决EMD的模式混叠现象，其主要原理［7］是：在不连续的信号中，高频分量的极值点间隔分布密集，低频分量的则分布稀疏。当在信号中加入白噪声，低频分量的极值点分布发生改变，整个频带中的极值点间隔分布均匀，从而避免了模式混淆。

EEMD分解［8］主要包括以下3个步骤：①往原始信号中添加均值为零，标准差为常数的白噪声，重复该步骤M次。②对每次加入白噪声的信号都分别进行EMD分解，得到各自不同的IMF分量和一个余项。③对M次分解对应的IMF进行总体平均运算，得到最终EEMD分解后的IMF分量。

EEMD分解中的添加噪声次数M由式⑴确定：其中，k为添加的白噪声序列幅值系数，e定义为输入信号与加噪分解后所有IMF和的标准差，其值越小证明分解精度越高。

1.2改进小波阈值算法

采用小波阈值法消噪，其效果主要取决于阈值的选取和阈值函数的确定。本文将分别从这两方面对该方法进行改进。

1.2.1阈值的选取

采用小波阈值法消噪，阈值的选择非常重要。若偏小，会保留部分噪声，使得消噪效果不佳；若偏大，会去除部分有用信号，使信号失真。因为噪声信号的模极大值随着分解层数的增大而减小［9］，所以对不同的分解层数采用相同的阈值处理，会在低频系数中滤除过多有用信息。由文献［10］可知噪声对应的第j+1层小波系数的最大值小于第j层小波系数的最大值的2/2倍。所以设定阈值选择规则如式（2）所示：

其中，λj为第j层分解尺度的阈值。而第一层分解尺度的阈值确定选用长度对数阈值法［10］，如式（3）所示：

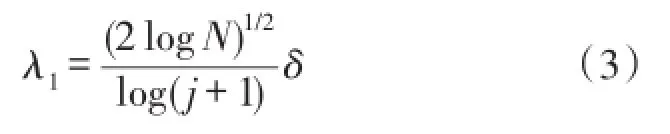
其中N为信号长度，j为小波分解尺度，δ为噪声标准方差，可由式（4）得到，式中d1为第一层分解尺度上的小波系数值。

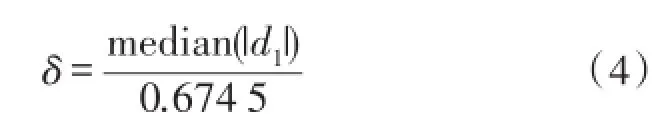
1.2.2阈值函数的选取

传统的小波阈值法一般都采用Donoho提出的软阈值或者硬阈值函数。用软阈值法消噪后的信号更光滑，连续性好，但是原小波系数和处理后的小波系数之间存在恒定的偏差，导致信号失真。而硬阈值虽然可以较好保留信号的特征，但是信号不连续，可能使重构信号产生震荡，出现Gibbs现象。结合两种方法的特点，本文确定的阈值函数［11］如式（5）所示：

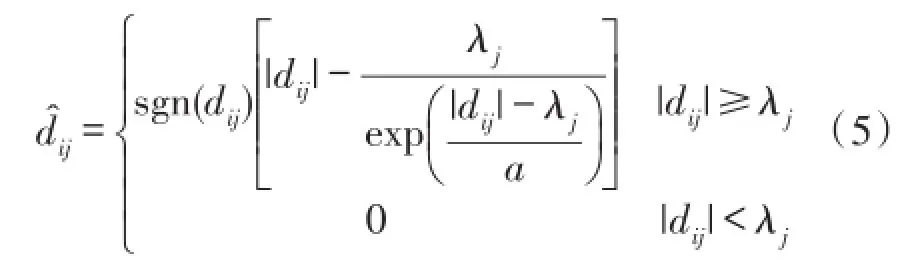
式中，dij为分解得到的第j层尺度上的第i个小波系数值，d̂ij为阈值处理后第j层尺度上的第i个小波系数值，a为正常数。由于上述阈值函数在±λij处是连续的，且当小波系数的绝对值满足|dij|时，阈值函数高阶可导。所以该方法可更有效地保留信号有效信息且保证信号的连续性。

1.3基于EEMD和改进小波阈值法的消噪方法

采用EEMD对信号进行分解时，得到多个IMF分量，前几个分量主要包含信号中的高频成分，后面的分量主要包含信号中的低频成分，噪声强度随着IMF层次的增加也会越来越弱，即信号的低频成分以有效信息为主，而高频成分含大量的噪声。传统基于EEMD的信号消噪方法常通过直接去除EEMD分解中的前几个高频IMF分量来消噪，但是这样会在去掉高频中的噪声成分的同时去除了其中的有效信息成分。

由于小波变换能够使信号的能量集中在小波域的一些大的小波系数中［12］，而噪声能量却分布在整个小波域内。因此，经小波分解后，信号的小波系数幅值要大于噪声的小波系数幅值。故可以选择一个合适的阈值对小波系数进行阈值处理，大于阈值则被视为信号的小波系数予以保留，小于阈值则被认为是噪声而被置零，从而达到消噪的目的。但是对于原始运动想象脑电信号，由于其幅值较小，单纯利用小波阈值消噪会在压制大部分噪声的同时去除了部分小幅度的有效信号。

针对以上情况，本文将EEMD和改进小波阈值法相结合，对EEMD分解后的高频分量进行小波阈值处理，再与未处理的低频部分相加进行重构得到消噪后的信号。通过两种方法互补的形式达到更有效的消噪效果，并且最大程度地保留信号的有效信息。具体实现步骤如下：①对原始信号进行EEMD分解，得到一系列IMF分量；②选择含噪声较大的前几项高频IMF分量，对其进行改进的小波阈值消噪；③将小波阈值消噪后的IMF分量以及其他IMF分量进行重构，得到消噪后的信号。

2　实验仿真

2.1标准信号加噪仿真实验

为了验证本文算法的消噪能力，首先采用MATLAB生成类似真实的脑电波形，与EEG信号的主要节律（δ、θ、α、β节律）对应，其中采样率为Fs= 250 Hz，时间为t=0∶1/Fs∶4，频率范围为2 Hz～30 Hz。该标准信号为［13］：

图1　原始标准信号和加噪后的信号

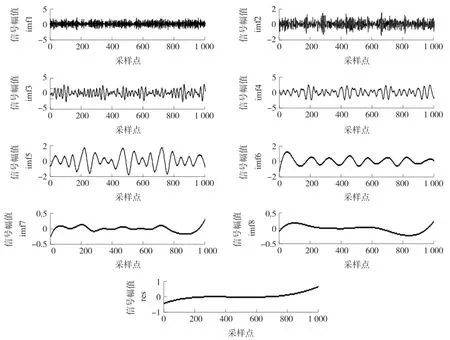
图2　EEMD分解后的各IMF分量

为了定量分析各方法的消噪效果，本文引入了信噪比（SNR）、均方根误差（RMSE）和峰值误差（PE）3个指标作为评价标准，其定义分别如式（6）～式（8）所示：

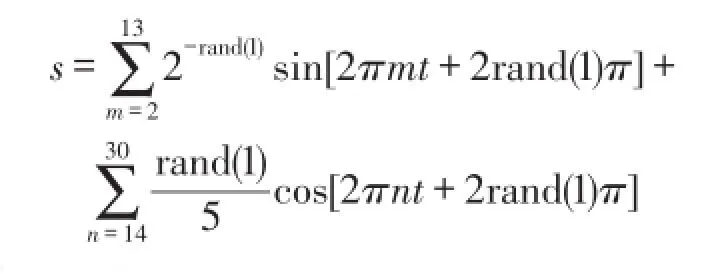
然后对标准信号加噪声x=awgn（s，n，‘measured’），此时加噪后的信号的信噪比为n dB；最后用各种消噪方法分别对加噪后信号进行消噪处理。图1是原始标准信号和加噪后的信号（信噪比为5 dB）。

首先对信号进行EEMD分解，得到了8层IMF分量，如图2所示。从图2可以发现，信号中的噪声主要集中在第一个高频IMF分量中。因此在对信号EEMD分解后只对第一个IMF分量进行改进小波阈值处理，处理后重构各分量得到消噪后的信号。经过多次实验比较，此次实验选用M为100，k为0.2。

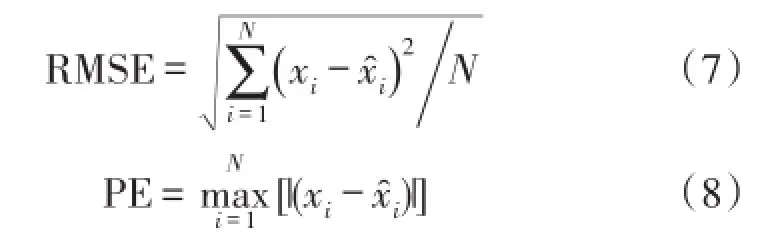
其中，N定义为信号的长度，xi为消噪前的信号，xˆi为消噪后的信号。信噪比越高，均方根误差和峰值误差越小说明信号的整体消噪效果越好。

用EEMD分解后直接舍弃高频IMF分量的方法、单独使用改进小波阈值法的方法、基于EMD与改进小波阈值法的方法和本文所提出的方法进行对比。各方法的消噪后效果图如图3所示。

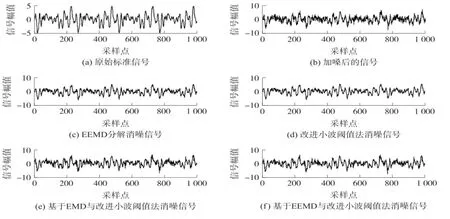
图3　4种方法的消噪效果对比图（噪声为5 dB）

从图3可发现，采用EEMD分解直接消噪后所得信号很平滑，但是部分细节信息缺失，即发生了信号失真。而单独采用改进小波阈值法消噪和基于EMD与改进小波阈值法相结合消噪所得信号细节信息较第一种方法保留的更好，但是信号还有很多毛刺。而基于EEMD与改进小波阈值法消噪后的信号不但更平滑，同时细节信息保留更完整。同时从表1中4种消噪方法处理后所得SNR、RMSE和PE值的数据对比可以定量证明本文的消噪方法的消噪效果优于其他3种消噪方法。

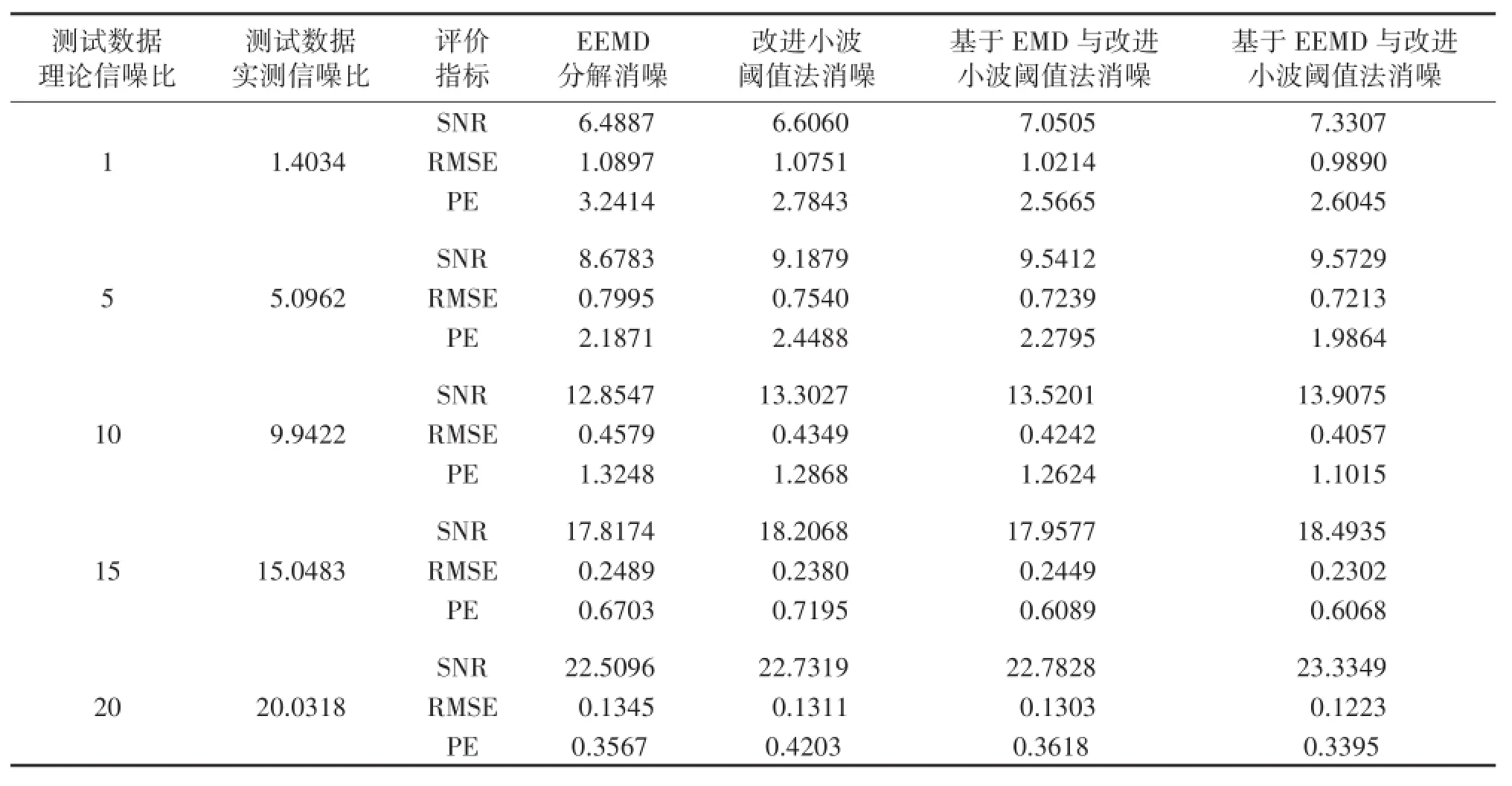
表1　4种消噪方法处理加了不同信噪比噪声的仿真信号的实验数据

2.2运动想象EEG消噪实验

为了验证本文所提出的方法对运动想象脑电信号的消噪效果，选用2003年脑-机接口竞赛的公开数据，采样频率为128 Hz，采集C3、C4和Cz 3个电极处的脑电信号。实验分为40组，每组有7次试验，每次试验持续9 s。0～2 s时，实验者保持休息放松状态；第2 s时，发出一声提示音并在显示屏上显示一个十字光标持续1 s，提醒实验者准备进入实验；第3 s后，显示屏上随机出现左右方向的箭头，实验者根据箭头指示想象与箭头相同方向的手运动，持续到第9 s，该试验完成。整个实验得到的280组试验数据分为140组训练数据和140组测试数据，而每组数据由C3、C4和Cz 3个通道数据组成。本文选取140组训练数据中的C3、C4和Cz 3个通道的运动想象脑电信号进行消噪处理。同时根据公式计算出各通道的140组训练数据消噪后的SNR、RMSE和PE值，再分别求这三个评价标准的均值和方差。图4是实验采集到的其中一段C3通道的原始MI脑电信号。

本次实验中选用了dB4小波对运动想象脑电信号进行两层分解。分别采用五种不同阈值法对140组C3通道的运动想象脑电信号进行消噪，得到它们的SNR、RMSE和PE值的均值和方差如表2所示。表中方法a、b、c是传统的软阈值法、硬阈值法和Garrote阈值法，而方法d是在软阈值法的基础上采用本文选用的新的阈值选取规则，方法e则是本文采用的改进阈值法。对比表中数据可以看出本文采用的改进阈值法的SNR最大且RMSE和PE最小，说明其消噪效果最好。另外对比方法a和方法d也证明新的阈值选取规则能更好地提高消噪效果。

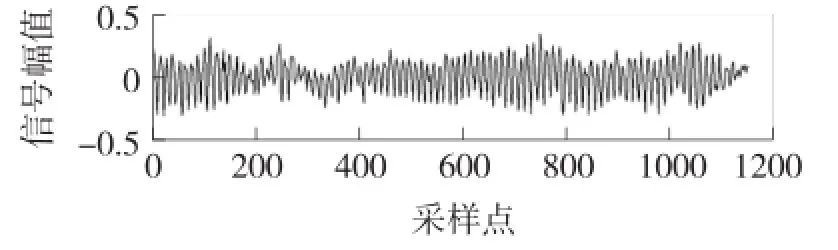
图4　原始C3通道的MI脑电信号

表2　单独使用不同阈值法消噪后的实验结果

由式（1）可知，EEMD分解的精度跟e有关，而e的值取决于添加的噪声次数M和添加的白噪声序列幅值系数k。图5、图6分别为不同k和M取值下本文方法消噪后的SNR和RMSE值。

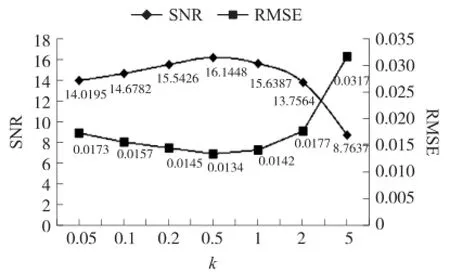
图5　不同k取值的SNR和RMSE值（M=100）

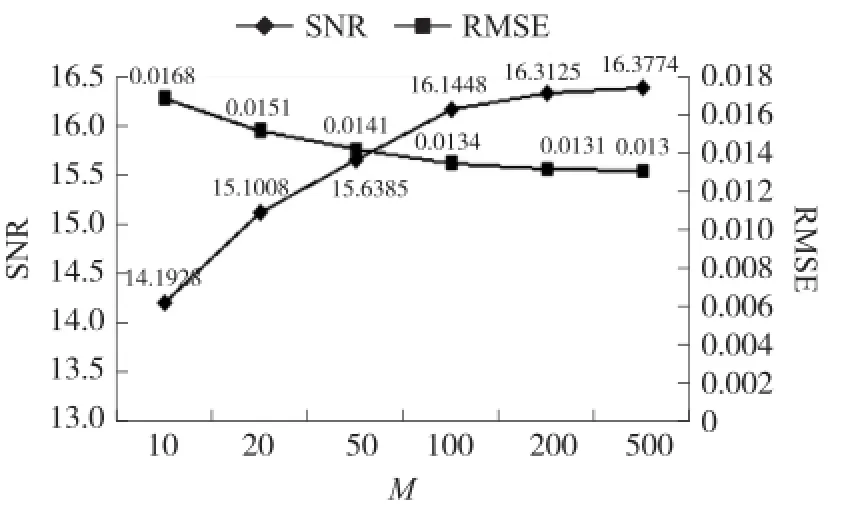
图6　不同M取值的SNR和RMSE（k=0.5）

从图5中可以看出当k越小，SNR越大且RMSE越小，这是因为k越小，则e越小，从而分解精度提高，故消噪效果越好。但是当k小于0.5时，其值越小，SNR越小且RMSE越大，这是因为k小到一定程度时又不足以引起信号局部极值点的变化，从而分解精度降低，故消噪效果变差。

而添加噪声次数M与e成反比，其值越大，e越小，从而分解精度越高。从图6可以看出当M越大时，SNR越大且RMSE越小，即消噪效果越好。但是随着M的不断增大，计算负担也会大幅增大。而从图6中可以发现当M大于100之后，SNR和RMSE变化幅度很缓慢，即消噪效果提高不大。综合考虑消噪效果和计算时间，本文此次实验选用M为100，k为0.5。

首先对信号进行EEMD分解，得到了9层IMF分量，如图7所示。从图中同样可以发现，信号中的噪声主要集中在第一个高频IMF分量中，故只处理第一个高频IMF分量。

采用不同的消噪方法对任意某段C3通道的原始MI脑电信号进行处理，得到消噪后效果图如图8所示。为了更清晰直观地看到各个方法消噪后效果图，此次消噪前在原始MI脑电信号中加入了信噪比为10dB的白噪声。分析效果图可发现，基于EEMD与改进小波阈值法消噪后的信号相比较单独采用改进小波阈值法消噪和基于EMD与改进小波阈值法相结合消噪所得信号更平滑，同时比采用EEMD分解直接消噪后所得信号的细节信息保留更完整，故而整体消噪效果优于其他3种。另外表3给出的是四种消噪方法分别处理C3、C4和Cz三个通道的140组训练数据所得的SNR、RMSE和PE的均值和方差。通过对比数据同样可以定量证明本文消噪方法的优越性。

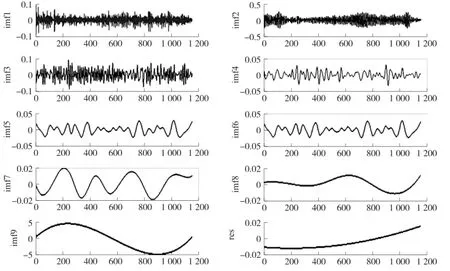
图7　EEMD分解后的各IMF分量

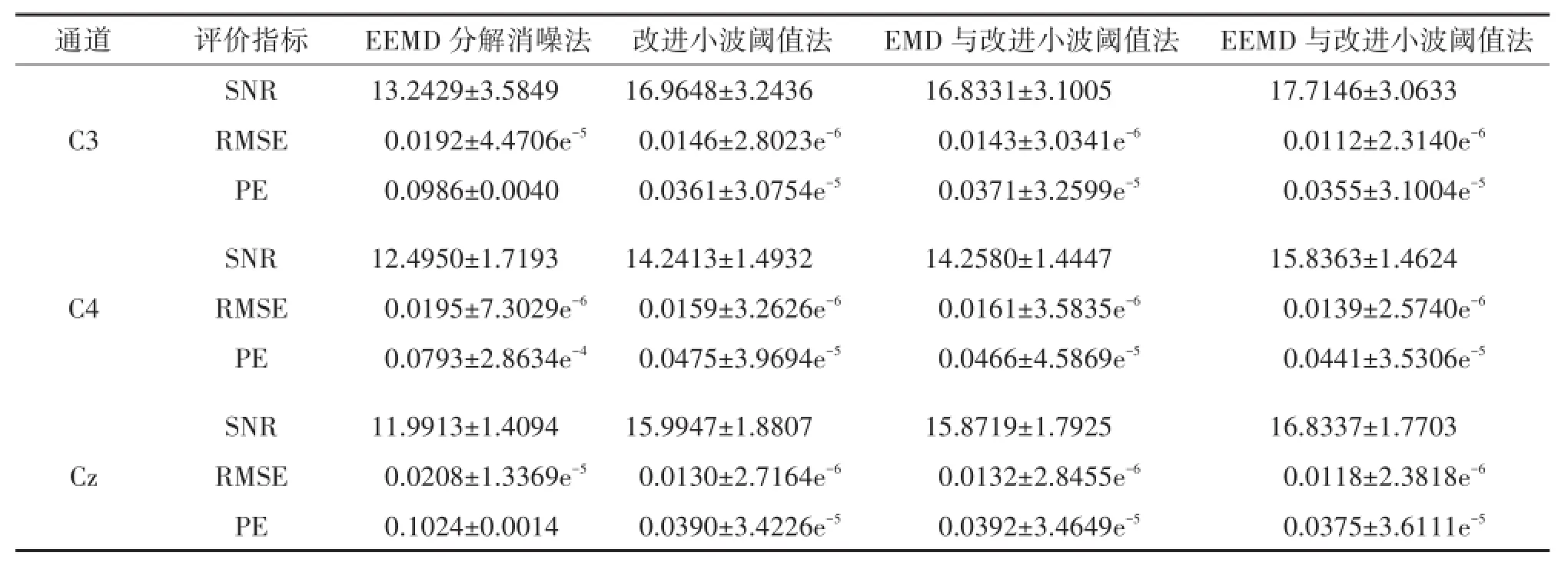
表3　4种消噪方法处理3个通道的140组数据的实验结果

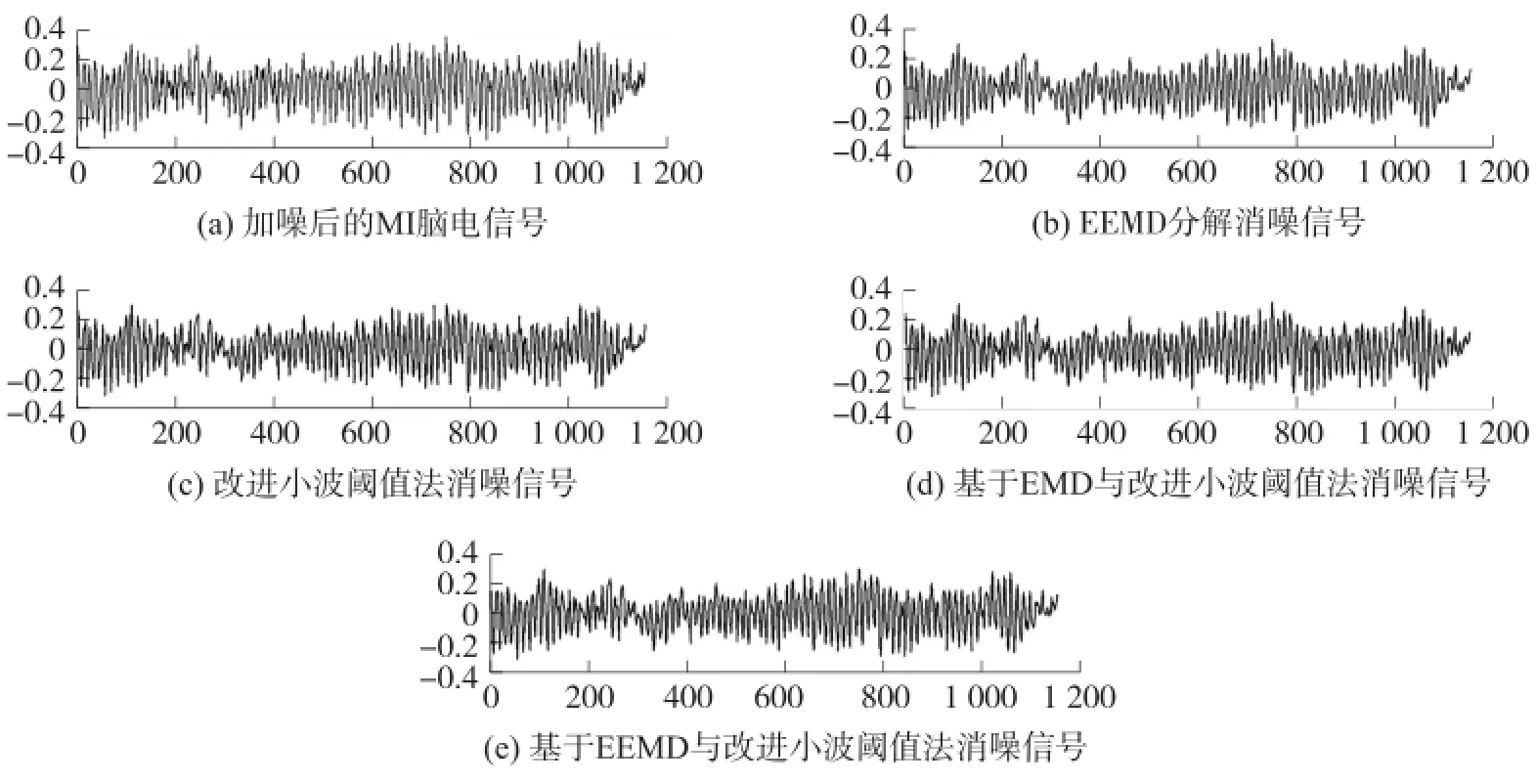
图8　4种方法的消噪效果对比图

3　结论

小波阈值法和EMD分解在信号消噪中有广泛的应用，特别是针对非平稳非线性信号。考虑到EMD分解的混叠现象和分别单独使用EMD分解与小波阈值法的局限性，本文提出了将EEMD分解与小波阈值法相结合的消噪方法。该方法是对EEMD分解后的前几个IMF高频分量进行改进小波阈值处理，从而保留了这些高频分量中的有效信息，同时减少了小波阈值法对弱能量有效信号的压制。通过实际数据的仿真证明，该方法的消噪效果优于单纯使用EEMD分解消噪、单独使用改进小波阈值消噪和EMD与改进小波阈值法相结合消噪这三种消噪法，故该方法有较强的实用性和优越性，为运动想象EEG的特征提取和分类研究奠定了坚实基础。

［1］Yu X，Chum P，Sim K.Analysis the Effect of PCA For Feature Re⁃duction in Non-Stationary EEG Based Motor Imagery of BCI Sys⁃tem［J］.Optik-International Journal for Light and Electron Optics，2014，125（3）：1498-1502.

［2］Albera L，Kachenoura A，Comon P，et al.ICA-Based EEG Denois⁃ing：a Comparative Analysis of Fifteen Methods［J］.Bulletin of the Polish Academy of Sciences：Technical Sciences，2012，60（3）：407-418.

［3］罗志增，周镇定，周瑛，等.双树复小波特征在运动想象脑电识别中的应用［J］.传感技术学报，2014，（5）：575-580.DOI：10.3969/j.issn.1004-1699.2014.05.001.

［4］马玉良，许明珍，佘青山，等.基于自适应阈值的脑电信号去噪方法［J］.传感技术学报，2014，27（10）：1368-1372.

［5］王姣，李振春，王德营.基于CEEMD的地震数据小波阈值去噪方法研究［J］.石油物探，2014，（02）：164-172.

［6］席旭刚，朱海港，罗志增.基于EEMD和二代小波变换的表面肌电信号消噪方法［J］.传感技术学报，2012，（11）1488-1493.

［7］朱晓军，吕士钦，余雪丽，等.基于改进EMD的脑电信号去噪方法［J］.计算机工程，2012，1（38）：151-156.

［8］Huang Z H，Fang B，He X P，et al.Image Denois-ing Based on the Dyadic Wavelet Transform and Improved Threshold［J］.Multireso⁃lution and Information Processing，2009，7（3）：4-7.

［9］许文博，武晓春，邢建平.一种新的小波阈值去噪方法［J］.兰州交通大学学报，2012，（3）：120-124.

［10］张建国，王文波.一种改进的经验模态分解消噪阈值函数［J］.中国科技论文，2013，（10）：1064-1067.

［11］杜修力，何立志，侯伟.基于经验模态分解（EMD）的小波阈值除噪方法［J］.北京工业大学学报，2007，（3）：265-272.

［12］Shao R P，Hu W T，Li J.Multi-Fault Feature Extraction and Diag⁃nosis of Gear Transmission System Using Time-Frequency Analy⁃sis and Wavelet Threshold De-Noising Based on EMD［J］.Shock and Vibration，2013，20（4）：763-78.

［13］罗志增，周瑛，高云园，等.基于双密度小波邻域相关阈值处理的脑电信号消噪方法［J］.模式识别与人工智能，2014，（5）：403-409.DOI：10.3969/j.issn.1003-6059.2014.05.003.

蔡慧（1991-），女，杭州电子科技大学硕士研究生，主要研究方向为生物信号分析及应用。caihui804@126.com；

马玉良（1976-），男，博士，杭州电子科技大学副教授，硕士生导师，主要从事生物信号检测与处理、仿生假肢及其控制、智能控制等相关研究，mayuliang@ hdu.edu.cn。

De-Noising Method of the MI EEG Based on EEMD and WT*

CAI Hui，MA Yuliang*，SHE Qingshan，GAO Yunyuan，Meng Ming
（Institute of Intelligent Control and Robotics，Hangzhou Dianzi University，Hangzhou 310018，China）

In order to eliminate the noise mixed in Motor Imagery Electroencephalogram（MI EEG）and retain useful MI EEG information，the paper puts forward a new MI EEG de-noising method based on ensemble empirical mode decomposition（EEMD）and improved wavelet threshold method.New threshold function and threshold selection rules are introduced to the improved wavelet threshold denoising method.Firstly，the MI EEG signal is decomposed by the EEMD.Then using the improved wavelet threshold method to denoise the high-frequency Intrinsic Mode Function（IMF）components.Finally，the processed high frequency IMF components and low frequency IMF compo⁃nents are reconstructed to get the denoised signal.The experimental results reveal that the proposed de-noising algo⁃rithm has perspective of higher SNR and lower RMSE compared to the other methods，including the pure EEMD，the pure improved wavelet threshold method，and the improved wavelet threshold method based on EMD.

mi eeg；de-noising；EEMD；wavelet threshold method；imf

TP391

A

1004-1699（2016）05-0716-07

项目来源：国家自然科学基金项目（61372023，61201302，61201300）；浙江省自然科学基金项目（LY14F030023）

2015-08-13修改日期：2015-12-02