基于弹性支撑与放大的宽频压电振动能量采集器模型与实验研究*

李萧均，王光庆，杨斌强（浙江工商大学信息与电子工程学院，杭州310018）

基于弹性支撑与放大的宽频压电振动能量采集器模型与实验研究*

李萧均，王光庆*，杨斌强（浙江工商大学信息与电子工程学院，杭州310018）

针对刚性支撑压电振动能量采集器工作频带窄、采集效率低等问题，提出了一种基于弹性支撑与放大的宽频压电振动能量采集器。利用有限元方法建立了宽频压电振动能量采集器的机电耦合模型，通过Ansys软件仿真分析了能量采集器结构参数对其频域输出特性的影响；根据力学和电学平衡方法建立了宽频压电振动能量采集器的集总参数机电耦合运动微分方程，利用4-5阶龙格库塔算法对方程进行了时域求解，仿真分析了能量采集器在不同结构参数下的振动位移、速度、输出电压和功率等性能。研制了弹性支撑和放大的宽频压电振动能量采集器原理样机，建立了样机系统实验平台，并对理论研究结果进行了实验验证，结果表明本文所提的宽频压电振动能量采集器具有工作频带宽、输出性能高等优点，适合为微电子器件进行供电。

压电能量采集器；弹性支撑与放大；有限元分析；机电耦合模型；宽频带

EEACC：2860Adoi：10.3969/j.issn.1004-1699.2016.05.012

压电振动能量采集器是利用压电陶瓷的正压电效应将环境中的振动能量采集转换成电能的新型微机电器件。由于它具有环保、无电磁干扰、构造简单、响应速度快、高能量密度等优点，在微机电、无线传感器网络和嵌入式系统中得到了广泛应用［1-2］。然而传统的单频能量采集器由于工作频带窄，只能在谐振频率附近很小的范围内具有有效地采集效果，在恶劣的环境下不易控制，难以输出稳定的功率。为此，有必要研究宽频压电采集技术，使压电采集器在较大的频率范围内产生谐振。

近年来，宽频压电振动能量采集器引起了国内外诸多学者的研究兴趣，并取得了一定的研究成果。Yang［3］等利用弹簧将两个悬臂梁压电振子连接起来构成了一个两自由度压电振子，通过调整结构参数使系统一阶、二阶谐振频率的间距减小形成一个宽频窗口。XUE［4］和TADESSE［5］等通过多模态方法对宽频进行了研究，理论分析并得出由多个压电振子组合而成的压电振子群可形成一个较宽的谐振频带，在环境振动频率不稳定的情况下可获得更多的能量。TANG［6］等研究了带有动态放大器的压电振动能量采集器并建立了数学模型，但忽略了能量采集器的机电耦合效应，因此模型无法精确预测和分析能量采集器的输出特性。Aldraihem和Baz［7］研究了带有动态放大器的压电振动能量采集器的机电耦合模型，并研究了动态放大器对输出功率的影响，但忽略了负载电阻和系统阻尼对系统输出特性的影响。文献［8］提出了一种改进的集总参数机电耦合模型，研究了带有弹性放大器的宽频压电采集器的输出特性，并对模型进行了验证，由于只在频域上进行了分析，虽然获得了较好的输出性能，但并没有考虑到当系统达到稳定状态时输出性能是否还能维持在较好的水平保持不变。

另外，从构造上讲，传统单频线性压电振动能量采集器的固定端通常采用刚性支撑方式，使之与宿主结构固定连接，如图1（a）所示。这种刚性支撑方式虽然可以较好地传递环境振动激励，但压电能量采集器的响应输出直接受到环境振动激励强度大小的影响，当环境激励强度较小时，压电能量采集器的响应输出将大大降低。为此，本文提出利用弹性支撑与放大的思路，将悬臂梁压电振动能量采集器固定在一个由质量-弹簧构成的弹性支撑机构上，形成一个两自由度宽频压电振动能量采集器，如图1（b）所示，通过弹性支撑机构将环境激励适当放大后激发悬臂梁压电振动能量采集器作高效的能量采集与转换。针对弹性支撑与放大的宽频压电采集器，首先通过有限元方法建立了宽频压电能量采集器的有限元分析模型，利用Ansys软件分析了采集器结构参数（如质量比、刚度比等）对系统频域输出性能的影响；其次，建立了宽频能量采集器的集总参数机电耦合数模型，根据力学和电学平衡原理建立了系统运动控制方程，数值分析了不同结构参数下能量采集器的时域输出性能。最后，搭建了宽频能量采集器的实验系统，通过实验验证了数值分析结果的正确性。

1　ES-PVEH结构

图1（b）是ES-PVEH结构示意图［9-10］，它是在RS-PVEH（图1（a））的基础上增加了一个由弹簧—质量块构成的弹性支撑与放大器系统，将压电悬臂梁的固定端与弹性支撑结构的质量块相连，构成一个两自由度宽频压电振动能量采集系统。图2是图1（b）的简化结构［11］，图中Mb、Kb和Cb分别为弹性支撑与放大器系统的等效质量、刚度和阻尼系数。Mt为压电悬臂梁末端集中质量块，R为负载电阻，双压电晶片PZT1和PZT2通过高强度粘结胶粘接在压电悬臂梁金属基板的上下表面，它们的极化方向相反，并通过串联连接方式与负载电阻R相连接构成封闭回路。i为流经负载电阻R上的电流。yb（t）和u（t）分别为Mb和基础的振动位移。其工作原理是施加基础振动位移u（t）的激励源，通过弹性支撑与放大系统将基础振动适当放大后传递到双压电片悬臂梁系统上，从而增大压电悬臂梁的激励强度，进而达到提高系统输出能力和拓宽谐振频带的目的。

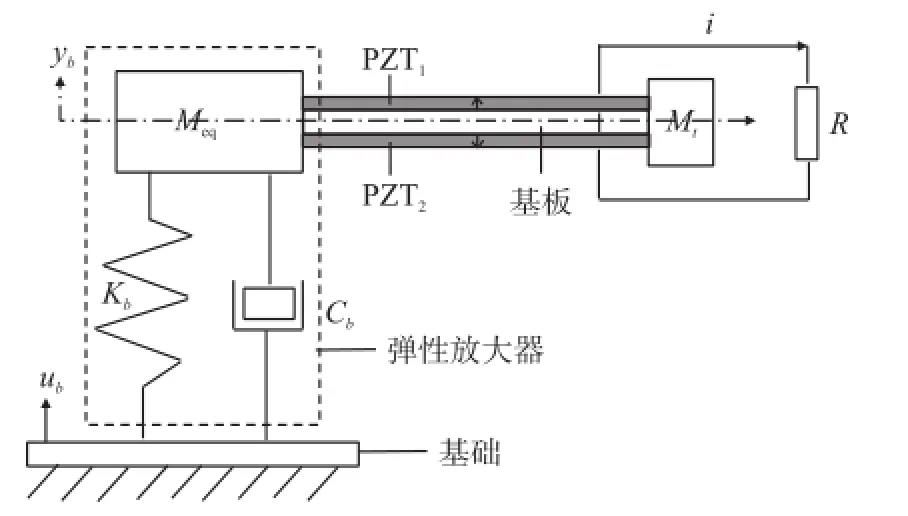
图2　ES-PVEH结构简图

2　采集器有限元机电耦合模型与分析

利用有限元对图1（b）所示宽频压电振动能量采集器进行实体建模，结果如图3所示，在有限元建模中，压电陶瓷PZT1和PZT2采用8节点六面体耦合场SOLID5单元进行建模；金属基板采用8节点线性结构SOLID45单元建模；质点单元MASS21用于弹性支撑与放大系统的集中质量Mb的建模；弹性单元COMBIN14用于弹性支撑与放大系统弹簧Kb和阻尼元件Cb的建模；负载电阻R采用电路单元CIRCU94单元类型建模，以便产生电压、电流和输出功率。压电陶瓷PZT1和PZT2的极化方向主要通过改变PZT1和PZT2压电陶瓷的压电常数d31、d33和d15的符号实现的。由于压电陶瓷和金属基板之间的粘结层厚度很小，模型中忽略粘结层的影响。

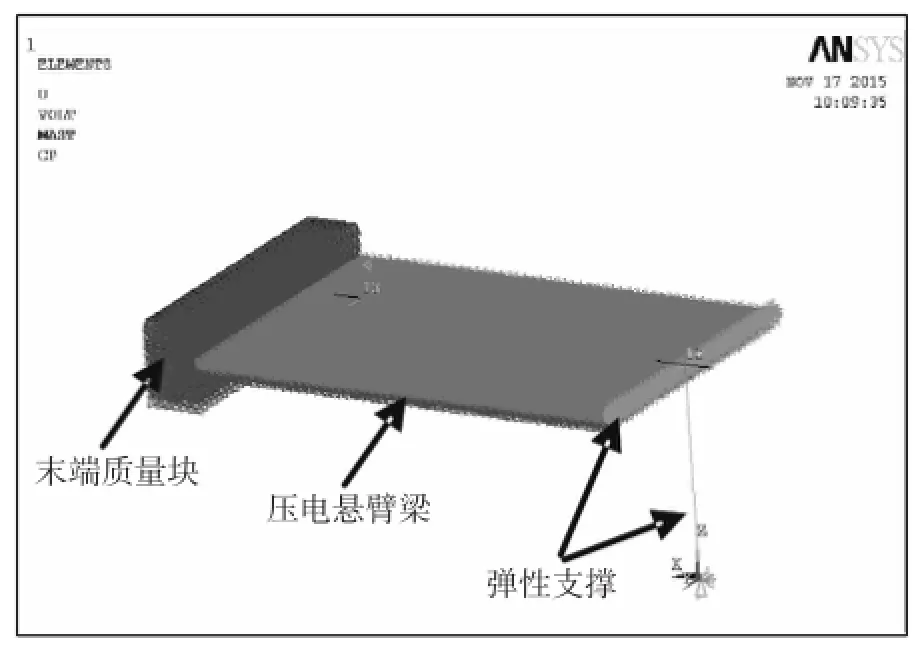
图3　ES-PVEH有限元机电耦合模型

在图3所示的有限元模型中，当弹性支撑与放大系统的质量块Mb趋于零（即Mb→0），弹簧刚度系数Kb趋于无穷大（即Kb→∞），弹性支撑变成刚性支撑（注：在本文中当Mb=1e-10时，即认为Mb→0；当Kb=1e+10时，即认为Kb→∞）。图4是RS-PVEH在基础加速度40 m/s2（下文未特别说明加速度均为40 m/s2）激励作用下，压电悬臂梁末端振动速度随负载电阻的变化情况，可以看出RS-PVEH的谐振频率为36.5 Hz，工作频带较窄，在负载电阻1 kΩ时，悬臂梁末端振动速度只有0.004 5 m/s。

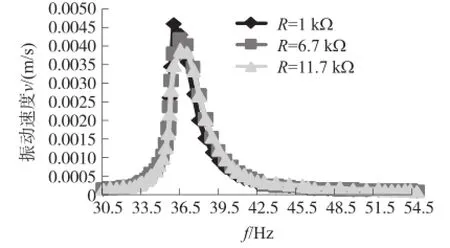
图4　RS-PVEH末端振动速度变化曲线

图5是ES-PVEH在刚度比r=10（r=Kb/Keq，Keq为压电悬臂梁的等效刚度），质量比a=10、20、30（a= Mb/Meq，Meq为压电悬臂梁的等效质量）时，采集器末端振动速度ν随激励频率ƒ的变化情况。由图5可知，每条曲线都存在左、右两个峰值，且随着质量比a的增大，左峰值幅值逐渐增大，在a=30时，悬臂梁末端速度达到0.016 m/s，是刚性支撑压电能量采集器末端速度的3.6倍。同时，速度响应曲线也随着质量比a的增大发生左移，峰值频率减小，两峰值之间的频率间距也逐渐变小，形成了一个宽频带窗口，这有利于提供能量采集器的工作范围。

图5　ES-PVEH末端振动速度变化曲线

图6和图7是负载电阻R为1 kΩ时，刚度比r=20、质量比a=10、20、30情况下ES-PVEH的输出电压和输出功率随频率的变化，为了便于观察，图中纵轴采用对数表示。

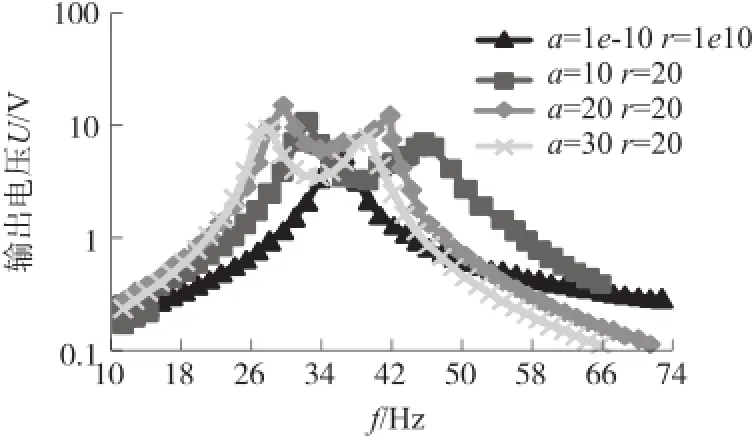
图6　ES-PVEH输出电压变化曲线

图7　ES-PVEH输出功率变化曲线

从图6～图7可以看出，随着质量比a的增大，曲线两峰值横轴间距变窄，逐渐形成一个宽频带窗口，输出电压和输出功率也随之增大。当a=r（如图中a=r=20）时，曲线两峰值的频率间距比a≠r时要小，但输出电压和输出功率却要大，这说明当放大器的固有频率和弹性支撑与放大系统的固有频率一致时，宽频率能量采集器的输出性能达到最佳。特别的，在质量比a=20时，ES-PVEH的输出电压和输出功率的谷值恰好等于RS-PVEH的输出电压和输出功率的峰值，说明选取合适放大器的结构参数，有利于能量采集器输出较高的电压和功率。图8是a=r=10时，在不同负载电阻下ES-PVEH的输出功率随频率的变化曲线图。从图8可以看出，当负载电阻的增大时，输出功率的变化趋势是先增大后减小，说明选取适当的电阻可以获得更为理想的输出功率。

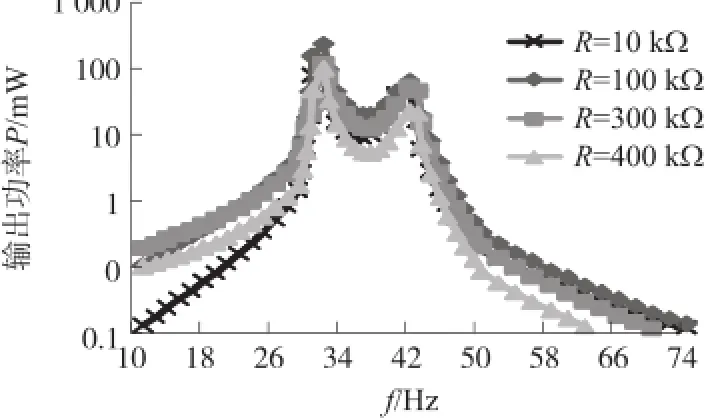
图8　不同负载时ES-PVEH的输出功率曲线

3　ES-PVEH运动微分方程及其解分析

为了更进一步的研究ES-PVEH的输出特性，建立图2所示的ES-PVEH的振动模型，如图9所示，图中压电悬臂梁的等效质量、刚度和阻尼分别为Meq、Keq和Ceq，压电陶瓷的夹持电容和机电转换系数分别为CP和α，V为压电采集器输出电压，ys为压电悬臂梁末端的振动位移。为了建立如图9所示的模型就需要确定双压电晶片悬臂梁系统的Meq、Keq、Ceq、CP等参数，具体可以参考文献［11-13］。

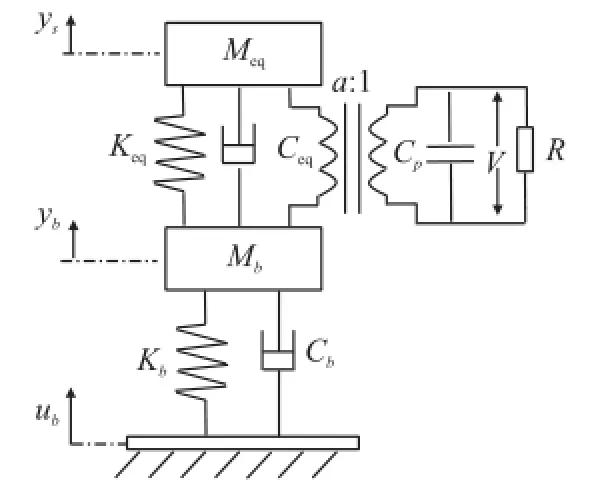
图9　ES-PVEH振动模型

根据力学和电学平衡原理，建立如图10的系统运动控制方程：

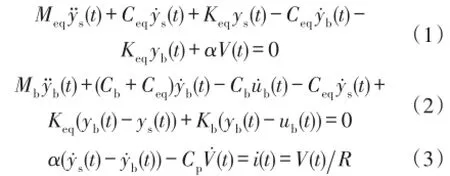
式中ü（t）=Asin（2πft）为基础激励加速度，A和f分别为其幅值和频率。采用龙格-库塔（Runge-Kutta）方法［14］进行求解式（4）可以得到系统在初始运动条件下的时域响应输出。本文在Matlab软件中采用4～5阶龙格-库塔算法ODE45进行求解。设置初始运动条件Y（0）=0，从而得到ES-PVEH的振动特性、电输出特性和负载特性曲线。图10是RS-PVEH在基础激励加速度为40 m.s-2，激励频率为40 Hz，负载电阻R为1 kΩ时，悬臂梁末端速度、采集输出电压和输出功率随时间的变化曲线图。

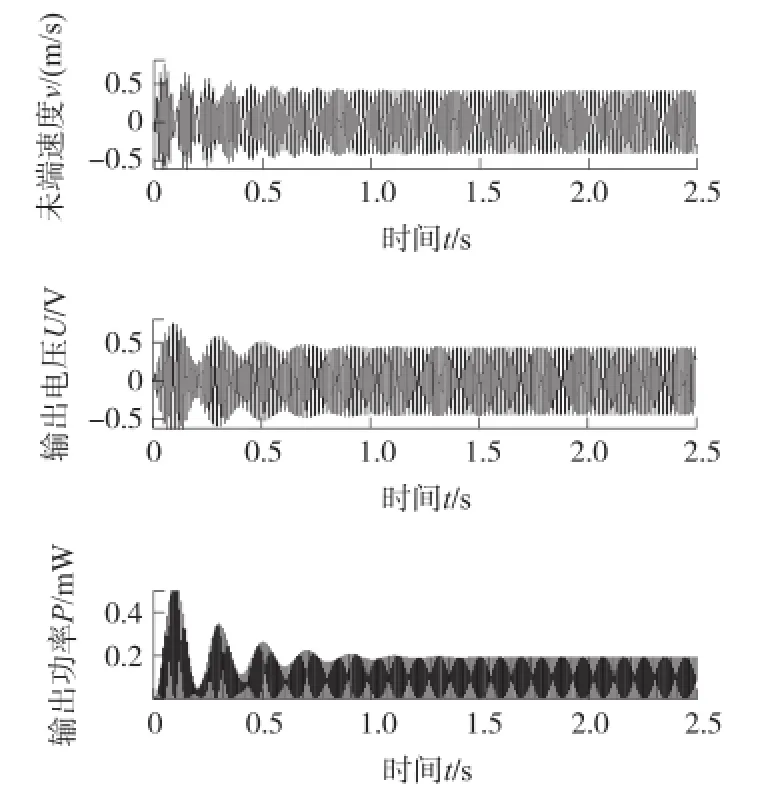
图10　RS-PVEH输出特性曲线图

从图10可以看到，稳态时RS-PVEH的末端速度为0.45 cm/s，输出电压为0.48 V，输出功率为0.2 mW。

图11为ES-PVEH在基础激励加速度为40 m/s2，激励频率为40 Hz，负载电阻R为1 kΩ时，在不同质量比和刚度比的情况下末端速度、输出电压和输出功率随时间的变化曲线图。图11（a）是a=r=10时的输出曲线，图中可以看出当趋于稳态时悬臂梁末端速度为0.5 cm/s，输出电压为3.7 V，输出功率为13.2 mW。图11（b）是a=r=20时的输出曲线，图中可以看出末端速度为0.7 cm/s，输出电压为8.3 V，输出功率为52 mW。图12（c）是a=r=30时的输出曲线，图中可以看出末端速度为1 cm/s，输出电压为11 V，输出功率为132 mW。这说明了随着质量比和刚度比的增大，ES-PVEH的末端速度、输出电压和输出功率均增大，这与有限元分析结果是一致的。

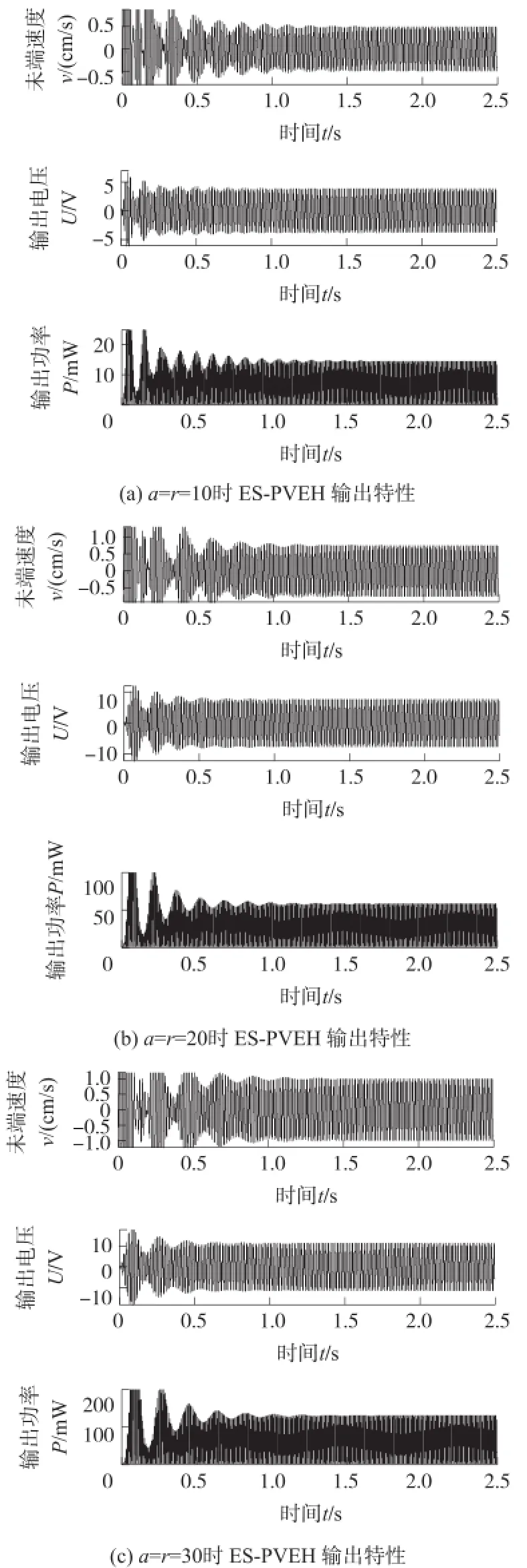
图11　不同a和r下ES-PVEH的输出特性

图12～图14分别是在a=10，r=20、30、80情况下，基础激励加速度为40 m/s2，激励频率为40 Hz时，ES-PVEH输出特性随时间的变化曲。

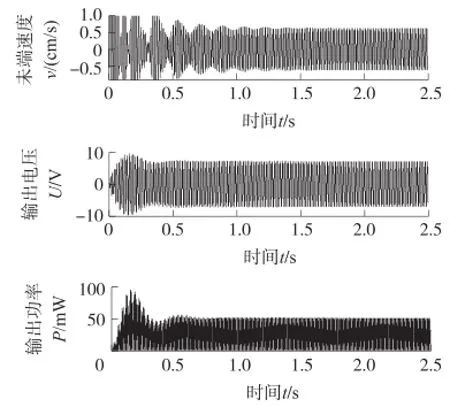
图12　a=10、r=20时ES-PVEH的输出特性

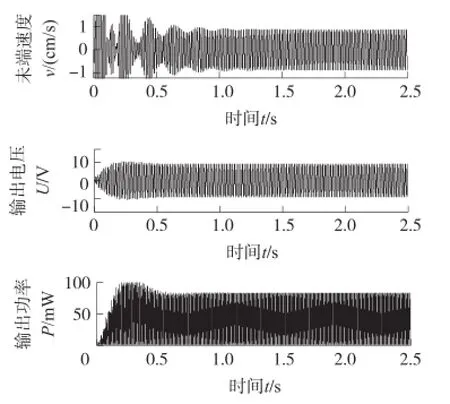
图13　a=10、r=30时ES-PVEH的输出特性

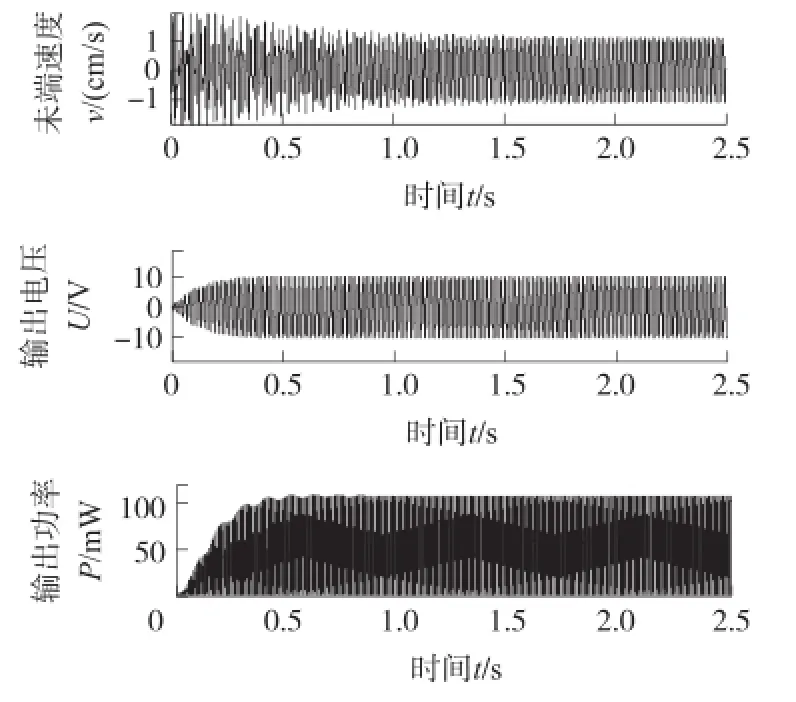
图14　a=10、r=80时ES-PVEH的输出特性

由图12可看出悬臂梁的末端速度在稳态时趋于0.6 cm/s，输出电压为7 V，输出功率50 mW。由图13可以看出，悬臂梁末端速度为0.8 cm/s，输出电压为9.5 V，输出功率为90.3 mW。由图14可看出，悬臂梁末端速度为1 cm/s，输出电压为10.2 V，输出功率为104 mW。通过这几个图的比较可以看出随着刚度比r的增大，对基础振动速度的放大能力增强，悬臂梁振动幅度、输出电压和输出功率都有所增大。和图11结果相比较，发现虽然在图14中刚度比r取到了80，但ES-PVEH输出效果并不如图11（c）中a=r=30的输出特性，这是因为当r=a时，基础振动频率与弹性放大器、悬臂梁的固有频率一致，整个宽频压电振动能量采集器系统处于谐振状态，系统的输出性能达到最佳。

4　实验研究

为了验证模拟仿真的准确性，研制了图15（a）和图15（b）所示的RS-PVEH和ES-PVEH原理样机，搭建了实验平台。ES-PVEH压电悬臂梁由两片压电陶瓷和磷青铜金属基板通过环氧树脂在120℃的高温条件下粘结固化而成。压电悬臂梁的等效刚度Keq为520 N/m、等效质量Meq为12.9 g，弹性放大器的质量Mb为123 g。

图15　研制的原理样机

图16是RS-PVEH和ES-PVEH的实验测试系统，信号发生器产生的正弦交流信号经功率放大器放大后激励激振器（型号：JZ-1）和基座，使之产生正弦波振动。选择502胶将RS-PVEH、ES-PVEH和加速度传感器（型号：YJ9A）并列粘接到基座上，RS-PVEH、ES-PVEH产生的电压波形通过示波器采集。基座振动加速度由加速度传感器采集后送入动态信号分析仪，分析后再经过INV1601型采集信息软件显示在屏幕上。试验中采样频率为1 000 kHz，加速度传感器标定值为57.2 mV/（m/s2）；速度传感器标定值为300 mV/（cm/s1）。

图16　实验测试系统

图17（a）、17（b）、17（c）分别为RS-PVEH在不同负载下的输出电压、输出电流、输出功率实验结果，为了便于实验结果的比较，实验中基础加速度取1 m/s2。从图17可看出，RS-PVEH的谐振频率为36.2 Hz，这与图4的有限元计算结果36.5 Hz是一致的。

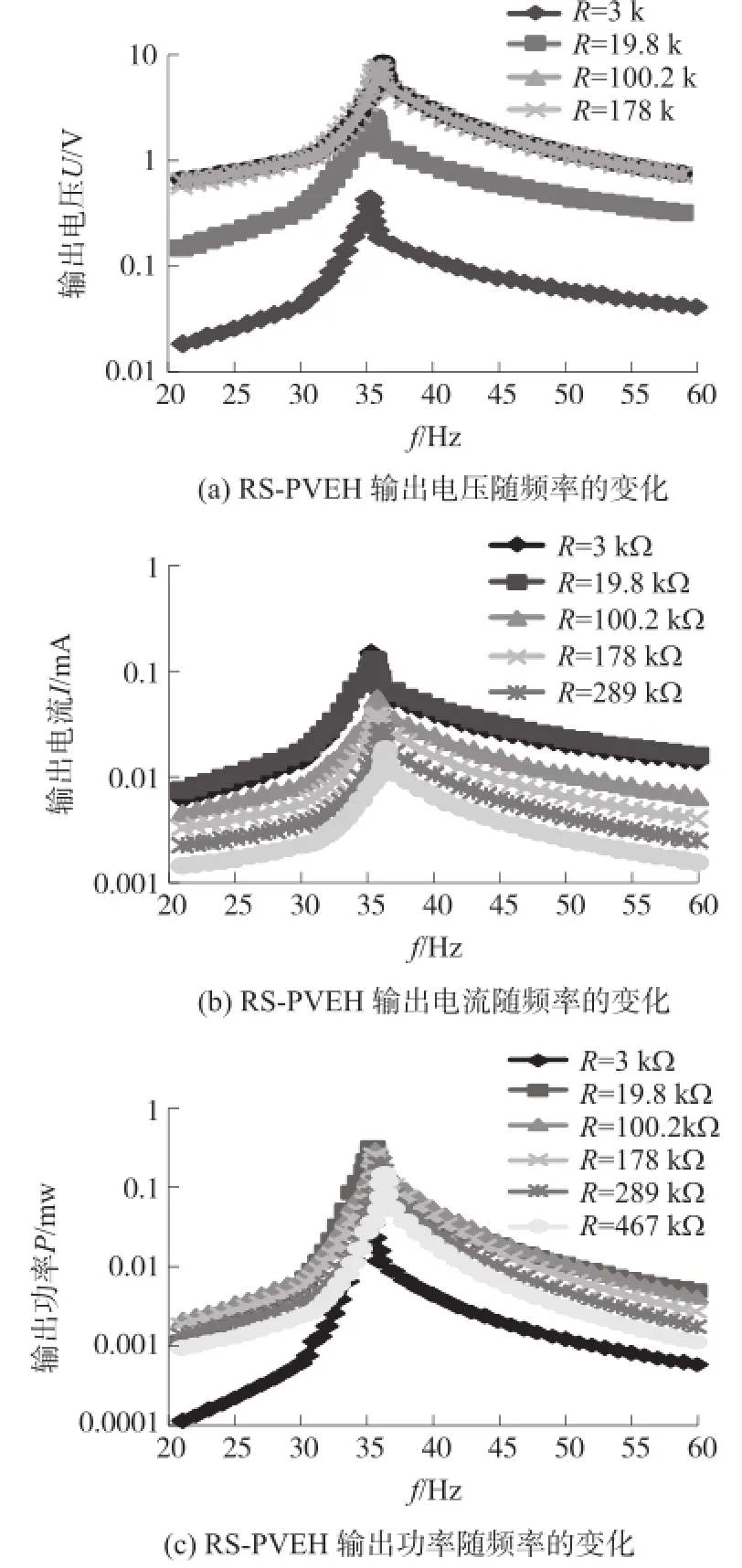
图17　不同负载下RS-PVEH输出特性实验结果

图18（a）、18（b）、18（c）分别为ES-PVEH在不同负载下的输出电压、输出电流、输出功率的实验结果，实验结果也是在加速度1 m/s2的激励条件下得到的。从图18可以看出，弹性放大器的加入，曲线存在左、右两个峰点，这有利于拓宽单频能量采集器的频带，在负载电阻R=3 kΩ时，曲线左、右两个峰值对应频率间隔达到14 Hz，而RS-PVEH对应的频带宽只有2 Hz，ES-PVEH的工作频带是RS-PVEH的7倍。此外，ES-PVEH在负载电阻R=3 kΩ时的输出电压、电流和输出功率分别是1.1 V、0.8 mA和0.88 mW，而RS-PVEH的输出电压、电流和输出功率分别是0.75 V、0.2 mA和0.15 mW，可见采用弹性支撑后，能量采集器的输出性能大大提高了。另外，由图18实验结果与图7有限元结果相比可知，有限元计算得到的ES-PVEH频带宽为13.8 Hz，并且在40 m/s2的激励加速度作用下，左、右峰值对应的输出功率分别为1300 mW和850 mW，对应单位加速度激励作用时输出的功率分别为0.812 5 mW和0.53 mW。而实验得到单位加速度激励作用下左、右峰值对应的输出功率分别为0.85 mW和0.52 mW，可见实验结果和有限元仿真分析结果比较吻合。另外，从图18实验结果还可看出，在激励频率40 Hz处，ES-PVEH能量采集器在负载电阻R=3 kΩ、单位加速度激励作用下的输出电压、电流和功率分别为0.19 V、0.15 mA和0.03 mW，分别对应40 m/s2加速度激励时的7.6 V、6 mA和48 mW，与图12（40 m/s2加速度激励时）在时域上的输出电压为7.7 V和输出功率50 mW也是一致的。综合上述实验与仿真结果的对比分析，验证了本文理论模型的正确性。

图18　不同负载下ES-PVEH输出特性实验结果

5　结论

提出了一种弹性支撑与放大的宽频压电振动能量采集器，理论与实验证明了基于弹性支撑与放大的宽频压电振动能量采集器具有提高输出性能和拓宽频带的作用。得到以下研究结论。

①和传统的刚性支撑压电振动能量采集器相比，弹性支撑与放大的宽频压电振动能量采集器使得原来的单一峰值变为左右两个峰值，拓宽了能量采集器的频带。

②弹性放支撑与放大器的加入，有效地提高了悬臂梁末端的振动速度，电输出特性（输出电压、输出电流、输出功率）。

③在a=r时，基础振动频率与系统的固有频率趋于一致，可以获得更佳的系统输出性能。

④当频率一定时，输出功率随负载电阻的增大先增大后减小，且谐振频率随负载电阻的增加略有增大。

［1］Beeby S P，Tudor M J，White N M.Energy Harvesting Vibration Sources for Microsystems Application［J］.Measurement Science and Technology，2006，17（12）：175-195.

［2］杜志刚，贺雪峰.带谐振腔的微型压电风能采集器［J］.传感技术学报，2012，25（6）：986-989.

［3］Yang Zengtao，Yang Jiashi.Connected Vibrating Piezoelectric Bi⁃morph Beams as a Wide-Band Piezoelectric Power Harvester［J］. Journal of Intelligent Material Systems and Structures，2009（20）：569-574.

［4］Xue H，Hu Y T，Wang Q M.Broadband Piezoelectric Energy Har⁃vesting Devices Using Multiple Bimorphs with Different Operating Frequencies［J］.IEEE Transactions on Ultrasonics Ferroelectrics，and Frequency Control，2008，55（9）：2014-2108.

［5］Tadesse Y，Zhang S，Priya S.Multimodal Energy Harvesting Sys⁃tem：Piezoelectric and Electromagnetic［J］.Energy Harvesting Technologies，2009，269（3/4/5）：3-39

［6］Tanx X D，Zuo L.Enhanced Vibration Energy Harvesting Using Dual-Mass Systems［J］.Journal of Sound and Vibration，2011，330（21）：5199-5209.

［7］Aldraihem O，Baz A.Energy Harvester with Dynamic Magnifier［J］.Journal of Intelligent Material Systems and Structures，2011，22（6）：512-530.

［8］王光庆展永振金文平，等.一种宽频压电振动能量采集器的解析模型与试验研究［J］.机械工程学报，2015，6（6）：155-164

［9］Tang X D，Zuo L.Enhanced Vibration Energy Harvesting Using Dual-Mass Systems［J］.Journal of Sound and Vibration，2011，330（21）：5199-5209.

［10］Arafa M，Akl W，Aladwani A，et al.Experimental Implementation of a Cantilevered Piezoelectric Energy Harvester with a Dynamic Magnifier［J］.Active and Passive Smart Structures and IntegratedSystem，2011，7977：79770Q-1-79770Q-9.

［10］王光庆金文平展永振，等.压电振动能量采集器的力电耦合模型及其功率优化［J］.传感技术学报，2013，26（8）：1092-1011.

［11］Shu Y C，Line I C.Analysis of Power Output for Piezoelectric En⁃ergy Harvesting System［J］.Smart Materials and Structures，2006， 15：1499-1512.

［12］Erturk A，Inman D J.An Experimentally Validated Bimorph Can⁃tilever Model for Piezoelectric Energy Harvesting from Base Exci⁃tations［J］.Smarts Materials and Structures，2009，18（2）：025009.

［13］方锦清姚伟光，逆算符方法求解非线性动力学方程及其一些应用实例［J］.物理学报，1993，42（9）：1375-1384.

李萧均（1992-）男，浙江工商大学在读研究生。主要从事传感检测与信号处理、压电振动能量采集器的理论与应用研究，276705188@qq.com；

王光庆（1975-），男，博士，教授，主要从事传感检测与信号处理、压电超声驱动器、压电振动能量采集器的理论与应用研究，kele76@163.com。

Model and Experimental Researches of a Broadband Piezoelectric Vibration Energy Harvester with an Elastic Support and Magnifier*

LI Xiaojun，WANG Guangqing*，YANG Binqiang
（School of Information and Electronic Zhejiang Gongshang University，Hangzhou 310018，China）

The piezoelectric vibration energy harvester with rigid support（RS-PVEH）has some disadvantages of nar⁃row operating band and low harvesting efficiency.In order to solve these issues，this article presents a broadband piezoelectric vibration energy harvester with an elastic support and magnifier（ES-PVEH）.The electromechanical coupling model of the ES-PVEH was established with finite element method，the effects of the structure parameters on the output performances in frequency domain were numerically analyzed.The lumped parameter governing equa⁃tions（LPGE）of the ES-PVEH was consequently derived based on the mechanical balance and electrical balance principles，and the time responses，such as the displacement，the tip velocity，the harvesting voltage and the output power of the ES-PVEH，were obtained by solved the governing equations with 4-5 order Runge-Kutta algorithm. Finally，the ES-PVEH prototype was developed and the experimental setup was presented，some experiments were carried out to testify the validities of the theoretical models.The results show that the ES-PVEH can not only broaden the operating frequency bandwidth，but also improve the output performance.

piezoelectric vibration energy harvester；elastic support and magnifier；finite element analysis；govern⁃ing equation；broadband

TN712.5

A

1004-1699（2016）05-0693-08

项目来源：国家自然科学基金项目（51277165）；浙江省自然科学基金项目（LY15F010001）

2015-12-01修改日期：2016-01-21