有限离散剪切波域的红外可见光图像融合
2016-10-26陈清江张彦博柴昱洲魏冰蔗
陈清江,张彦博,柴昱洲,魏冰蔗
(西安建筑科技大学 理学院,陕西 西安 710055)
有限离散剪切波域的红外可见光图像融合
陈清江*,张彦博,柴昱洲,魏冰蔗
(西安建筑科技大学 理学院,陕西 西安 710055)
针对目前图像融合过程中的不足之处,结合有限离散剪切波具有高的方向敏感性和抛物尺度化特性,提出了一种有限离散剪切波变换下的图像融合算法。首先对严格配准的多传感器图像进行有限离散剪切波变换,得到低频子带系数和不同尺度不同方向的高频子带系数;然后对低频子带系数采用全局特征值和像素点之间的差异性与区域空间频率匹配度相结合的融合算法,高频方向子带系数采用方向权重对比度与相对区域平均梯度和相对区域方差相结合的方案;最后通过有限离散剪切波逆变换得到融合图像。实验结果表明,与其他的融合算法相比较,本文算法不但有良好的主观视觉效果,而且3幅图像的客观评价指标分别平均提高了0.9%、3.8%、3.1%,2.6%、3.8%、2.9%和1.5%、125%、59%,充分说明了本文融合算法的优越性。
图像融合;有限离散剪切波;对比度;区域平均梯度;平移不变性
1 引 言
图像融合是指采用特定的算法将两幅或多幅图像合成为一幅更精准、更具可靠性图像的过程。通过图像融合技术可以最大限度地获取对目标或场景信息的完整描述,更适合人的视觉及计算机检测、分类、识别及处理。这种技术已广泛应用于医学、智能机器人、遥感等领域。
多尺度变换是将待融合图像分解为不同尺度、不同方向上的一系列代表不同特征的子图像,然后选取合适的融合规则,对子图像进行运算选取,最后将处理后的系数进行逆变换得到重构图像。它与人眼视觉系统对事物的认知过程非常相似,因此将多尺度变换的思想应用于图像融合领域将得到符合人类视觉特征的融合图像。1987年,Mallat将多尺度分析思想引入小波分析的研究中,提出了多分辨率分析[1]的概念。因此用小波变换[2-4]来处理图像信号,可以较好地提取图像边缘轮廓等细节信息。然而,传统的小波变换只能捕捉水平、垂直和对角3个方向的信息,并不能很好地表示图像的“线奇异性”,在处理二维信号时有一定的局限性。为此,人们先后提出了DWT[5]、CT[6-7]、NSCT[8-9]、 DTCW T[10]、NSST[11]等变换,从移变性到平移不变性的发展,使得它们具有更好的方向选择性,可以更稀疏地表达图像的细节纹理信息,在图像融合中取得了较好的主观视觉效果;但其缺点是计算复杂度较高,且分解的方向数有限。随后,S.Häuser和G.Steidl[12]证明并构造了有限维欧式空间中parseval框架的离散剪切波,简称有限离散剪切波(FDST),它不仅满足平移不变性,同时保持了DWT及NSCT的良好特性,并且由于FDST在分解、重构过程中采用快速Fourier变换算法,因此也具备了较好的运算效率。
多尺度变换将源图像分解成低频信息和不同尺度不同方向上的高频信息,低频子带是源图像的近似,包含了图像的主要信息;高频子带包含了源图像的细节信息。传统的融合策略不能有效地提取图像的边缘轮廓等细节图像,模糊了源图像的清晰部分,容易引入虚假信息,导致融合结果失真。为改善图像融合后的质量,本文对于低频采用全局特征值和像素点之间的差异性与区域空间频率匹配度相结合的融合算法;对于高频采用将相对区域平均梯度和相对区域方差与方向权重对比度[13]相结合算法。实验结果表明,该融合算法能有效地提取图像的互补信息,保留多幅图像的共同特征及边缘纹理等细节信息,融合效果优于其他算法。
2 有限离散剪切波变换
2.1剪切波变换[12]
设剪切型矩阵和抛物型矩阵分别为:
(1)
式中,p∈R+,s∈R。∀ψ∈L2(R2),对ψ进行膨胀、剪切及平移得到ψp,s,t,并且:
(2)
通过对ψp,s,t进行二维傅里叶变换,得到L2(R2)中任意f的连续剪切波变换及对应parseval等式,通过定义小波函数和冲击函数可将频域平面分成不同的区域,包括水平锥面、垂直锥面、锥面交叉线和低频部分。如图1所示。

图1 不同区域的频域平面 Fig.1 Frequency domain plane in different regions
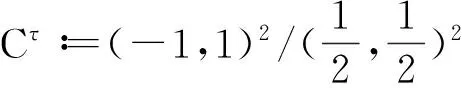
(3)
对低频部分上的剪切波,使用加细函数φ可使得φ(x)的平移变换为Ttφ(x)=φ(x-t)。
2.2有限离散剪切波

(4)
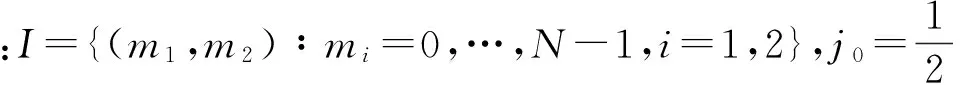
(5)
因此离散剪切波就可表示为:

(6)


图2 测试图像及重构图像 Fig.2 Test image and reconstructed image

图3 第一层和第二层分解的方向子带 Fig.3 Directional subband of the first level and second level decomposition
3 图像融合策略
FDST的分解融合过程:首先对源图像进行FDST分解,得到不同尺度不同方向的低频和高频子带系数;其次对低频和各高频系数分别选取不同的的融合规则以及对各系数进行运算选取,最后应用有限离散剪切波逆变换得到重构图像。以两幅图像为例,算法主要步骤如下:

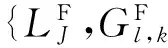
3.1低频子带融合策略
低频图像是源图像的近似,在原始图像中所占能量比例较大,包含了源图像的主要信息。以往的低频融合策略如区域能量忽略了黑暗部分,区域方差只增强了边缘效果,并没有提高整体的融合效果。 为改善图像融合后的质量,受文献[14]启发,低频部分采用全局特征值和像素点之间的差异性与区域空间频率匹配度相结合的融过算法。具体融合规则如下:
(1)设A、B为低频图像,区域窗口大小为N×N,为了提高融合图像的对比度,低频不再采用简单的加权平均或区域能量的方法,这里给出了一种自适应的加权融合方法,权重参量计算如下:
(7)
(8)
式中,λA、λB表示图像A、B的全局特征值,全局特征值反映图像的一般背景亮度,比灰度均值和中位数更能反映图像的整体特性,计算如下:
(9)

(2)区域空间频率反映图像的局部特征,往往区域信息丰富、有效信息多的区域空间频率大,这里结合区域空间频率构造了一种区域空间频率匹配度融合方法。首先计算A、B在(i,j)点的区域空间频率:
SFA(i,j)=
(10)
SFB(i,j)=
(11)
式中,A(i+m,j+n),A(i+m-1,j+n),A(i+m,j+n-1),B(i+m,j+n),B(i+m-1,j+n),B(i+m,j+n-1)为A,B在(i+m,j+n),(i+m-1,j+n),(i+m,j+n-1)点的灰度值,定义与A、B相关的区域空间频率匹配度:
(12)
式中,N(i,j)为以(i,j)点为中心的N×N区域。当A和B相接近时,MA,B(i,j)接近于1;当A和B相差较大时,MA,B(i,j)接近于0。令I(0.5 (13) 3.2高频子带融合策略 高频图像包含了源图像的边缘细节信息,对高频系数的选取直接影响融合后图像的清晰度,以往采用区域方差、区域平均梯度、空间频率等方法能用不同的方式反映图像的详细信息,并且可以区分图像的清晰和模糊区域,上述3种方法均能全面反映图像特征,不同的方法也有不同的融合效果。但是在大多数现有的融合算法中通常只采用其中一种融合算法,这样会丢失源图像的细节信息,在主观视觉效果和客观评价指标之间不能达到最佳的折衷。本文将方向权重对比度与相对区域方差和相对平均梯度结合起来,克服了单一融合算法的缺点,有效地改善了融合后图像的质量。具体步骤如下: (14) (15) (16) (17) (18) (3)选取融合后的高频系数,为改善融合效果引入参量r(0 (19) 4.1不同变换域下同一种融合策略的图像融合 为说明有限离散剪切波变换的优越性,在不同的变换域下采用同一种本文提出的融合策略,对红外与可见光图(图4(a)、4(b))进行融合比较。具体分别对传统融合策略下采用平稳小波变换(SWT)、离散小波变换(DWT)、非下采样轮廓波变换(NSCT)、双树复小波变换(DTCWT)、非下采样剪切波变化(NSST)、有限离散剪切波变换(FDST)进行比较。仿真的实验机器为Thinkpad E420,软件是Matlab2014a,对主观视觉效果及对相应的客观评价指标(信息熵EN,互信息量MI,边缘相似度QAB/F)和运行时间进行比较说明。融合结果依次为图4(c)~4(h)所示。 图4 不同小波域在文章融合策略下对红外与可见光图的融合结果 Fig.4 Infrared and visible image fusion results using fusion strategy of this paper in different wavelet domain 图4是红外与可见光图像的融合结果,从融合结果及细节放大效果中可以看出:图4(c)、4(d)、 4(e)、4(f)和4(g)都不同程度地提取了源图像的互补信息,视觉效果较源图像都有所改善,但是图像整体昏暗,模糊了源图像的清晰部分;而4(h)中船的轮廓清晰可见,对比度适中,细节纹理特征突出,提取到了目标的主要信息,有更好的视觉效果。这说明FDST在图像融合过程中比其他变换域具有更大的优越性。相应的客观指标评价结果如表1。 表1 不同小波域下对红外与可见光图的融合结果比较 由表1可以看出,在Infrared and visible图的6种融合结果中,DWT边缘相似度高于SWT,但SWT的熵值和互信息量却优于DWT。NSCT、DTCWT和NSST的熵值、互信息量和边缘相似度相互接近。而FDST的各项客观评价指标均优于其他变换域下的融合结果。其中熵值、互信息量和边缘相似度分别平均提升了26.3%、131.6%和63.6%。从运行时间来看,有限离散剪切波变换在视觉效果和客观指标大大提升的同时,又有相对较高的运算效率,这充分说明了FDST在图像融合中的优越性。 4.2不同文献算法的融合结果比较 不同的融合策略应用于不同的变换域会有不同的融合效果。这部分主要用4种不同的融合算法对3幅红外与可见光图(图5(a)、5(b),6(a)、6(b),7(a)、7(b))进行了融合比较。具体包括:非下采样剪切波变换下低频采用空间频率与平均梯度自适应加权,高频采用区域方差取大的融合算法[16](NSST_ HSGLRV);下采样分数阶小波变换下低频采用区域能量取大法,高频采用区域方差匹配度的融合算法[17]( FRWT_HRELV);有限离散剪切波变换下低频采用梯度加权,高频采用区域标准差取大的融合算法[18](FDST_LGHRS); 有限离散剪切波变换下低频采用全局特征值和像素点之间的差异性与区域空间频率匹配度相结合,高频采用方向权重对比度与相对区域平均梯度和相对区域方差相结合的融合算法(FDST_LGVHC)。融合结果依次为图5(c)~5(g)、6(c)~6(g) 、7(c)~7(g)所示。 图5 不同小波域在不同融合策略下对红外与可见光图(5)的融合结果 Fig.5 Infrared and visible image(5) fusion results using different fusion strategies in different wavelet domains 图6 不同小波域在不同融合策略下对红外与可见光图(6)的融合结果 Fig.6 Infrared and visible image(6) fusion results using different fusion strategies in different wavelet domains 从融合结果及细节放大效果可以看出,图5(c)~5(f)、6(c)~6(f)、7(c)~7(f)都提取到了目标的互补信息,但图像的细节反差和明暗保持各有不同。如图5(f)在整体色度和饱和度方面比图5(c)、5(d)、5(e)表现更充分,草木中的细节纹理信息更为精确,充分保持了源图像的主要信息。图6(c)图像色度发生改变,图6(d)图像整体模糊,而图6(e)和6(f)效果明显改善,尤其是图6(f)中的电脑、瓶子、柜子等都清晰可见,对比度适中,细节纹理突出,视觉效果良好。图7(c)和7(d)虽然能够将目标信息融入到融合图像中,但都模糊了源图像的清晰部分。图7(e)融合效果有所改善,与图7(e)相比,图7(f)更加清晰自然,区域特征明显,边缘轮廓保持完整。这说明在有限离散剪切波变换下低频采用全局特征值和像素点之间的差异性与区域空间频率匹配度相结合,高频采用方向权重对比度与相对区域平均梯度和相对区域方差相结合的融合算法是可取的。相应的客观评价指标见下表2。 由表2可以看出:在Infrared and visible image(6)的融合结果中,FDST_LGVHC除了熵值略低于FDST_LGHRS,其它指标均优于NSST_ HSGLRV,FRWT_HRELV,FDST_LGHRS。其中熵值、互信息量和边缘相似度分别平均提升了0.9%、3.8%和3.1%。而在Infrared and visible image(5)和Infrared and visible image(7)的融合结果中,FDST_LGVHC的熵值、互信息量和边缘相似度均是最优的。并且Infrared and visible image(5)的各项客观评价指标分别平均提升了2.6%、3.8%和2.9%;Infrared and visible image(7)的各项客观评价指标分别平均提升了1.5%、125%和59%。从运行时间来看,在有限离散剪切波变换下采用本文的融合策略不但客观指标均有所提高,而且具有很好的时效性,进一步说明了本文算法的可取性。 表2 不同小波域在不同融合策略下对红外与可见光图的融合结果比较 结合有限离散剪切波具有平移不变性和抛物尺度化特性,提出了利用有限离散剪切波对源图像进行多尺度变换,并对低频子带系数和各方向高频子带系数采用不同的融合策略,最后应用有限离散剪切波逆变换重构得到融合图像。实验结果表明:与其它融合算法相比,本文提出的融合算法能够有效提取图像的边缘、轮廓等细节纹理信息,具有良好的主观视觉效果。在客观评价指标上,除了个别指标不是最优,其它指标均优于其它算法,而且图像的客观评价指标整体分别平均提高了0.9%、3.8%、3.1%,2.6%、3.8%、2.9%和1.5%、125%、59%。总体而言,本文融合算法能够得到较好的融合效果,具有较高的运算效率。 [1]杨桄,童涛,陆松岩,等.基于多特征的红外与可见光图像融合[J].光学 精密工程,2014,22(2):489-496. YANG G,TONG T,SONG-YAN L U,etal.. Fusion of infra- red and visible images based on multi-features[J].Optics&PrecisionEngineering,2014,22(2):489-496.(in Chinese) [2]MEHRA I,NISHCHAL N K. Wavelet-based image fusion for securing multiple images through asymmetric keys[J].OpticsCommunications,2015,335:153-160. [3]ZHANG H,CAO X. A way of image fusion based on wavelet transform[C]. 2013 IEEE 9th International Conference on Mobile Ad-hoc and Sensor Networks,IEEE Computer Society,2013:498-501. [4]CHENG J,LIU H,LIU T,etal.. Remote sensing image fusion via wavelet transform and sparse represent- tation[J].IsprsJ.Photogrammetry&RemoteSensing,2015,104:158 173. [5]YANG Y. Multimodal medical image fusion through a new DWT based technique[C]. 2010 4th International Conference on Bioinformatics and Biomedical Engineering(iCBBE),IEEE,2010:1-4. [6]WANG X,LIU Q,WANG R,etal.. Natural image statistics based 3D reduced reference image quality assessment in contourlet domain[J].Neurocomputing,2015,151:683 691. [7]杨粤涛,朱明,贺柏根,等.采用改进投影梯度非负矩阵分解和非采样Contourlet变换的图像融合方法[J].光学 精密工程,2011,19(5):1143-1150. YANG Y T,ZHU M,HE B G,etal.. Fusion algori- thm based on improved projected gradient NMF and NSCT[J].Opt.PrecisionEng.,2011,19(5):1143-1150. (in Chinese) [8]陈小林,王延杰.非下采样变换的红外与可见光图像融合[J].中国光学,2011,4(5):489-496. CHEN X L,WANG Y J. Infrared and visible image fusion based on nonsubsampled Contourlet transform[J].ChineseOptics,2011,04(5):489-496.(in Chinese) [9]张蕾,金龙旭,韩双丽,等.采用非采样Contourlet变换与区域分类的红外和可见光图像融合[J].光学 精密工程,2015,23(3):810-818. ZHANG L,JIN L X,HAN SH L,etal.. Fusion of infrared and visual images based on non-sampled contourlet transform and region classification[J].OpticsCommunications,2015,23(3):810-818.(in Chinese) [10]RANGASWAMY Y,RAJA K B,VENUGOPAL K R. FRDF:face recognition using fusion of DTCWT and FFT features[J].ProcediaComputerScience,2015,54:809-817. [11]陈贞,邢笑雪.基于非下采样Shearlet变换与压缩感知的图像融合[J].液晶与显示,2015(6):1024-1031. CHEN ZH,XING X X. Image fusion algorithm based on non-subsampled Shearlet transform and compressed sensing[J]. 2015,30(6):1024-1031.(in Chinese) [12]HAUSER S,STEIDL G. Convex multiclass segmentation with shearlet regularization[J].InternationalJ.ComputerMathematics,2013,90(1/2):62-81. [13]蒲恬,方庆喆,倪国强.基于对比度的多分辨率图像融合[J].电子学报,2000,12:116-118. PU T,FANG Q ZH,NI G Q. Contrast-based multiresolution image fusion[J].ActaElectronicaSinica,2000,12:116-118. (in Chinese) [14]ZHAO CH H,GUO Y T,WANG Y L. A fast fusion scheme for infrared and visible light images in NSCT domain[J].InfraredPhysicsandTechnology,2015,72:266-275. [15]LIU X,ZHOU Y,WANG J. Image fusion based on Shearlet transform and regional features[J].AEU-InternationalJ.ElectronicsandCommunications,2013,68(6):471-477. [16]石智,张卓,岳彦刚.基于Shearlet变换的自适应图像融合算法[J].光子学报,2013,42(1):115-120. SHI ZH,ZHANG ZH,YUE Y G. Adaptive image fusion algorithm based on shearlet transform[J].ActaPhotonicaSinica,2013,42(1):115-120. (in Chinese) [17]徐小军,王友仁,陈帅.基于下采样分数阶小波变换的图像融合新方法[J].仪器仪表学报,2014(9):2061-2069. XU X J,WANG Y R,CHEN SH. Novel image fusion method based on downsampling fractional wavelet transform[J].ChineseJ.ScientificInstrument,2014(9):2061-2069.(in Chinese) [18]陈广秋,高印寒,刘广文,等.有限离散剪切波域结合区域客观评价的图像融合[J].吉林大学学报(工学版),2014,44 (6):1849-18 59. CHEN G Q,GAO Y H,LIU G W,etal.. Image fusion based on area objective assessment in finite discrete shearlet transform domain[J].J.JilinUniversity(Engineering and Techonlogy Edition),2014,44(6):1849-1859.(in Chinese) Fusion of infrared and visible images based on finite discrete shearlet domain CHEN Qing-jiang*, ZHANG Yan-bo ,CHAI Yu-zhou, WEI Bing-zhe (College of Science,Xi′an University of Architecture and Technology,Xi′an 710055,China)*Correspondingauthor,E-mail:qjchen66xytu@126.com Aiming at the deficiency of the current image fusion process, combining with good directional sensitivity and parabolic scaling properties of Finite Discrete Shearlet Transform(FDST), a new image fusion algorithm based on FDST is proposed. Firstly, the registration multi sensing images are decomposed by FDST, and the low frequency sub-band coefficients and high frequency sub-band coefficients of different scales and directions are obtained. The fusion principle of low frequency sub-band coefficients is based on the method of combining the differences between global attribute and each pixel with region spatial frequency matching degree. As for high frequency sub-band coefficients, sum of the directional weight contrast can be adopted as the fusion rule, which combines with the relative region average gradient and relative region variance. Finally, the low frequency information and high frequency information are reconstructed to image by Finite Discrete Shearlet Inverse Transform. The results indicate that the algorithm proposed in this paper has a good subjective visual effect, and its quality indexes has been increased averagely by 0.9%、3.8%、3.1%, 2.6%、3.8%、2.9% and 1.5%、125%、59% respectively compared with other fusion algorithms, which shows that the algorithm is superior to other fusion algorithms. image fusion;finite discrete shearlet;contrast;regional average gradient;shift-invariant 2016-04-18; 2016-05-11 陕西省自然科学基金资助项目(No.2015JM1024;No.2013JK0568) 2095-1531(2016)05-0523-09 TP391.4 Adoi:10.3788/CO.20160905.0523 陈清江(1966—),男,河南信阳人,博士,教授,主要从事小波分析、图像处理与信号处理方面的研究。E-mail:qjchen66xytu@126.com Supported by Shaanxi Provincial Natural Science Foundation of China(No.2015JM1024;No.2013JK0568)

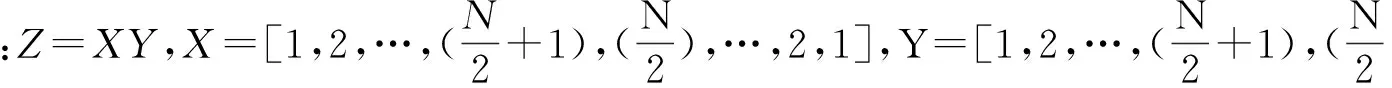


4 仿真实验及结果分析





5 结 论

