Non-Carathéodory域中重点为无穷缺项函数系{zτnlogsnz}的逼近

马薛珂

(昆明理工大学 数学系　云南 昆明 650500)



Non-Carathéodory域中重点为无穷缺项函数系{zτnlogsnz}的逼近

马薛珂

(昆明理工大学 数学系云南 昆明 650500)

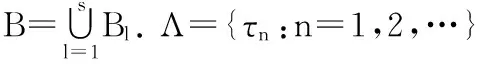
Non-Carathéodory域； 重点； Lp(B)空间； 逼近

0　引言

函数系在Banach空间中的完备性问题,是逼近论中的经典问题.文献[1-3]介绍了函数系在复平面的无界曲线上、可测集上、具有非连通补集的有界区域上以及在无界区域上的逼近问题.近年来,关于函数系的逼近问题仍是许多学者研究的热点.文献[4-5]考虑了复指数系的不完备性、最小性以及加权指数多项式的逼近.文献[6-7]推广到研究函数系在C0(E)空间中的完备性问题,文献[8]得出多元复指数系不完备的充要条件及其闭包的特征.

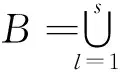
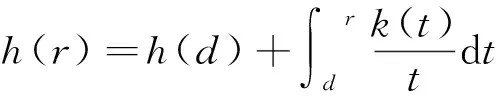
(1)

(2)

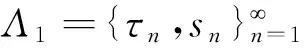
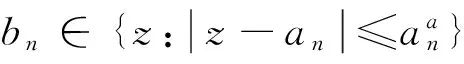
函数系{zτnlogsnz}的指数{τn}有重点,且重点个数趋于无穷的情况下,研究Non-Carathéodory域上函数系{zτnlogsnz}在Banach空间Lp(B)上的完备性问题,有以下定理1.

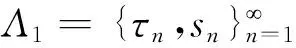
1　辅助引理

为证明定理,先论述并证明以下几个辅助引理.本文中Ci表示常数,每次出现不必相同.

引理1[1]若h(r)满足式(2)的条件,则可知函数系{zτnlogsnz}在Lp(B)空间中.

引理2多项式系{zn}在Lp(B)空间中是完备的.

引入典型乘积，

(3)

注解1典型乘积φ(z)是绝对一致收敛的,对于任意小的正数ε,可知F(w)在Ωε内是有界解析的.

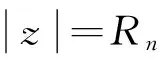
C是一个与w和Rn都无关的常数,并且此时φ满足

tanφ<ε/(Dsinα).

(4)

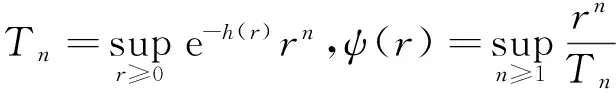
由Carleman定理可以得到以下引理.

若1≤p<,且,设q(z)∈Lq(B),定义G(w)=∬B′q(eξ)F(w-ξ)dξ1dξ2.其中ξ=ξ1+iξ2,z=eξ,B′是闭集合B在ξ=logz下的像,则可知集合B′一定是位于带状的区域且α1是常数).集合B是有界的单连通区域,引入2个带型区域：).

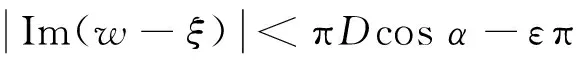
引理7若G(w)≡0,那么如果q(z)∈Lq(B),则有等式∬Bq(z)zndxdy=0,z=x+iy.

证明类似文献[7]中引理2.13的证明过程.

引理8如果函数系{zτnlogsnz}在解析函数空间Lp(B)中完备的充要条件是：已知Lq(B)是Lp(B)的共轭空间,对于任意的q(z)∈Lq(B),有等式∬Bq(z)zτnlogsnzdxdy=0成立,则可推出q(z)≡0.

由Riesz-Fischer定理可推出引理8成立.

2　定理的证明

证明假设M(Λ1)在Lp(B)空间中是不完备的.由引理1可知,函数系{zτnlogsnz}在LP(B)空间中.又由引理8知,若证明函数系{zτnlogsnz}在解析函数空间Lp(B)中完备,只需证明对任意的q(z)∈Lq(B),对所有的zτnlogsnz,有等式∬Bq(z)zτnlogsnzdxdy=0成立,则推出q(z)≡0即可.由引理2知,多项式系{zn}在Lp(B)空间中完备,故只需证明∬Bq(z)zndxdy=0即可[11].

由上述引理及G(w)的定义可知

其中C是一个与Rn和w都无关的常数.由0<(1-η)nR≤Rn≤nR,可知

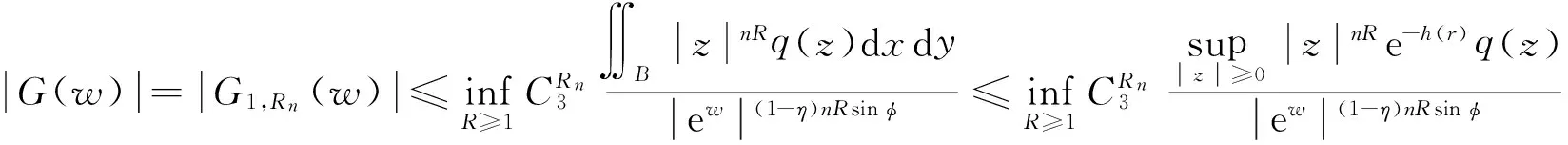
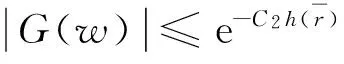
(5)

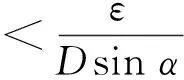
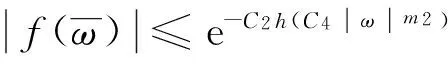
(6)

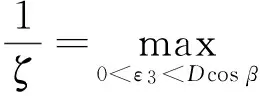
故∫，其中C5是一个正数,

且与y无关.故∫,即

∫.

(7)

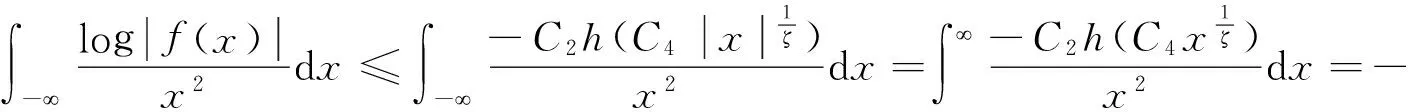
(8)

由引理7可知,G(w)≡0可推出∬Bq(z)zndxdy=0.故可知定理成立.

[1]沈燮昌.关于函数系{zτnlogjz}在复数平面上的无界曲线上的完备性问题[J].数学学报,1963,13(2):170-192.

[2]沈燮昌.关于函数系{zτnlogjz}在复数平面上的区域中的完备性问题[J].数学学报,1963,13(3):405-418.

[3]沈燮昌.用函数系{zτnlogjz}来逼近复平面上的函数[J].数学学报,1964,14(3):406-414.

[4]DENG G T. Weighted exponential polynomial approximation[J]. Sci China Ser A,2003,46(2):280-287.

[5]DENG G T. Incompleteness and minimality of complex exponential system[J]. Sci China：Ser A, 2007, 50(10),1467-1476.

[6]YANG X D, TU J. On the completeness of the system {tλn}inC0(E)[J]. J Math Anal Appl, 2010, 368(2): 429-437.

[7]YANG X D. On the completeness of the system {tλnlogmnt} inC0(E)[J].Czechoslovak mathematical journal,2012,62(137):361-379.

[8]王翠巧,邓冠铁.加权Hardy空间中解析函数的唯一性及多元指数多项式的加权逼近[J].北京师范大学学报(自然科学版),2015,51(4):334-339.

[9]ZIKKOS E.On a theorem of norman levinson and a variation of the fabry gap theorem[J].Complex variables,2005,50(4):229-255.

[10]沈燮昌.关于广义狄里希莱多项式展开的余项估计[J].北京大学学报,1962,3:199-211.

[11]沈燮昌.复变函数逼近论[M].北京:科学出版社,1992:88-121.

(责任编辑：方惠敏)

On the Completeness of the Function System {zτnlogsnz} with Infinite Multiplicity in Non-Carathéodory Region

MA Xueke

(DepartmentofMathematics,KunmingUniversityofScienceandTechnology,Kunming650500,China)

Non-Carathéodory region; multiplicity;Lp(B) space; completeness

2016-03-30

马薛珂(1990—),女,河南安阳人,硕士研究生,主要从事复分析研究,E-mail:1542032159@qq.com.

O174.5;O174.52

A

1671-6841(2016)03-0039-04

10.13705/j.issn.1671-6841.2016061

引用本文：马薛珂.Non-Carathéodory域中重点为无穷缺项函数系{zτnlogsnz}的逼近[J]．郑州大学学报(理学版)，2016，48(3)：39-42.