环球飞车的动力学分析

苗英恺

（濮阳职业技术学院实训中心，河南濮阳 457000）

教学讨论

环球飞车的动力学分析

苗英恺

（濮阳职业技术学院实训中心，河南濮阳 457000）

分析了环球飞车在水平轨道上圆周运动的力学原理.利用车身在运动中的受力和力矩的平衡，重点分析了飞车在上半球水平轨道上运行的受力情况、速度的极值及车身的倾角.计算出飞车水平运行轨道的最大高度.

环球飞车；圆周运动；质心运动定理；轨道极限高度

我们都看过“环球飞车”杂技表演，多辆高速飞驰的摩托车在直径仅有6.5 m的球形金属笼内上下翻飞、交叉穿越，十分惊险.车手精准的控制，高超的技艺，令观众叹为观止.目前，这项极限运动的最新吉尼斯世界纪录，是由濮阳水秀杂技团2013年在濮阳水秀龙珠馆内创造的.表演中，车手驾驶摩托车可以在球内水平、竖直、倾斜的任何平面上运行，11辆摩托车最后分成上、中、下三层，做水平方向的圆周运动，其中最上层的4辆摩托车高度竟然超过了球体的赤道而进入到上半球内，持续时间长达30 s，简直令人难以置信.

摩托车在上半球水平面内做圆周运动时，球壁对车轮的支持力方向倾斜向下，为什么车不会掉下来呢？摩托车在球内水平圆周运动轨道的极限高度又是多高呢？

文献［2］对此进行了分析.但文章将人车系统看做质点，仅讨论了轨道的极限高度，没有讨论轨道的高度与车速和车身倾角的关系.本文运用动力学理论对飞车在上半球的运行情况进行了进一步的讨论，对轨道的高度与车速和车身倾角的关系进行了具体分析.

飞车在球内的运动不但涉及到速度和受力问题，还涉及到车身的平衡问题，故不能将人车系统当作质点来看待.如图1所示，点O为球心，球体的半径为R，人车质量为m，h为人车系统质心相对高度.飞车在球内做水平圆周运动时，人车除受重力mg外，车轮还会受到球壁的压力FN和静摩擦力Ff，设车轮与球壁间的静摩擦系数为μ0.

图1 飞车水平圆周运动的受力模型

图中标出了飞车分别在球体的下部、中部和上部运行的三个水平轨道，其中在中、下二个轨道上的圆周运动不再讨论［1，3］，下面重点讨论飞车在上半球水平轨道上的运行情况.

设飞车在上半球以O′为圆心的水平面上作圆周运动.O点是球体的球心，A为运动轨道上任意一点，OA与O′O的夹角为α（α为钝角）.摩托车运动速度为υ，车身与竖直方向的倾斜角度为θ，与OA间的夹角为γ.FN和Ff的参考方向如图中所示.

根据达朗贝尔原理，有

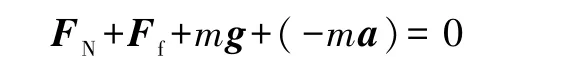
a为向心加速度，（-ma）为离心惯性力.

由于车手上身一般是趴在摩托车上的，人车系统重心较低.为了便于分析，忽略h对向心力的影响.可列出水平和竖直方向的受力平衡方程：

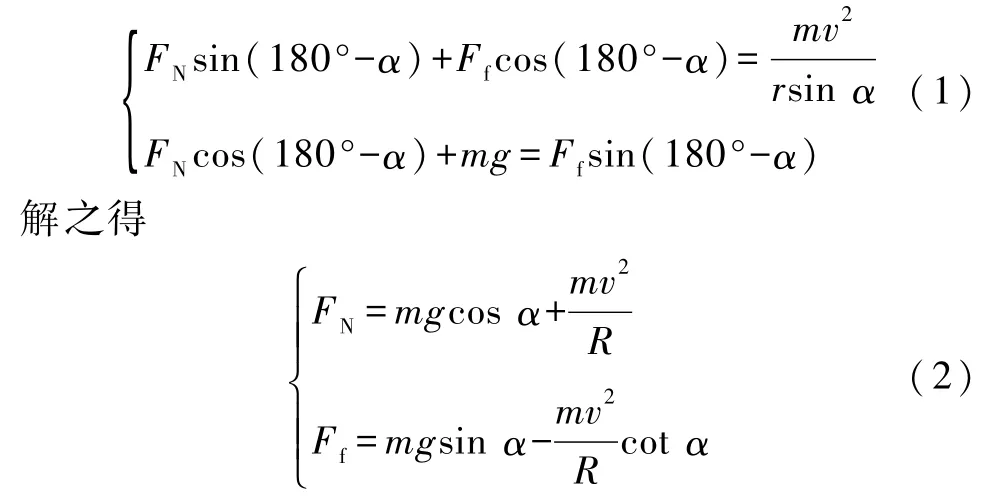
根据质心运动定理，忽略车轮旋转和车身圆周运动所产生的角动量，可列出相对于质心的力矩平衡方程：

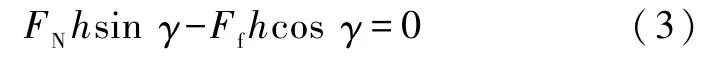
可得出

由于此时摩托车没有打滑，所以μ0FN≥Ff即

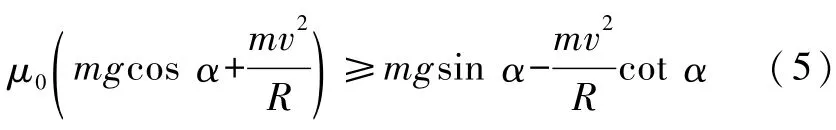
可解出

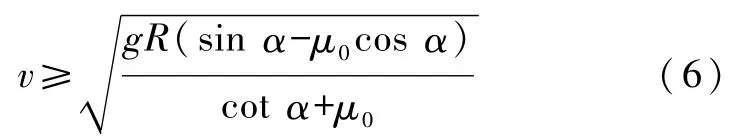
上式表明，飞车在该轨道上稳定运行有一个最小速度，即

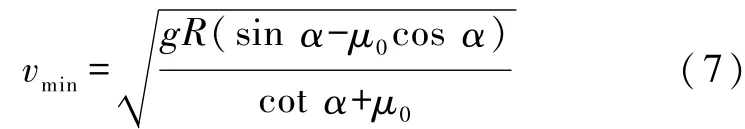
由式（4）可求出v=vmin时飞车的倾斜角：

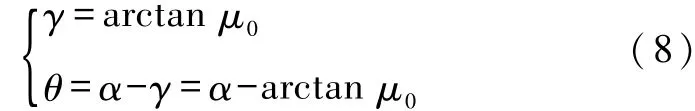
又由式（2）可知，飞车在上半球水平轨道上运行，90°＜α＜180°，则sin α＞0，cot α＜0，所以，Ff始终为正值.

以上分析可见，该轨道上v只有最小值，无最大值.即当速度v＜vmin时，μ0FN＜Ff，摩托车会打滑.

当v≥vmin时，无论多大，μ0FN≥Ff均成立，摩托车则不会打滑，可以安全运行，此时，FN和Ff均为正值，方向不变.

由式（4）可求出，随着速度v的增大，γ的极限值为

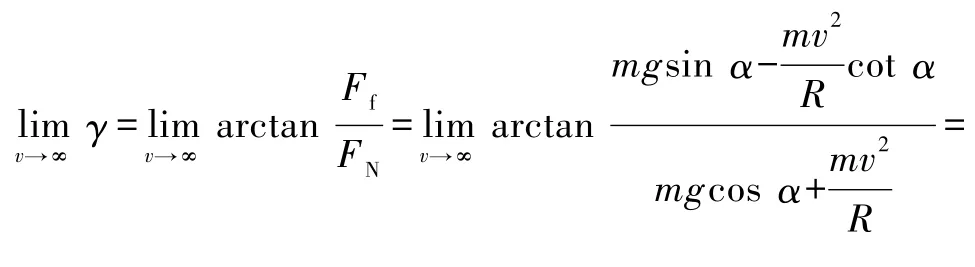
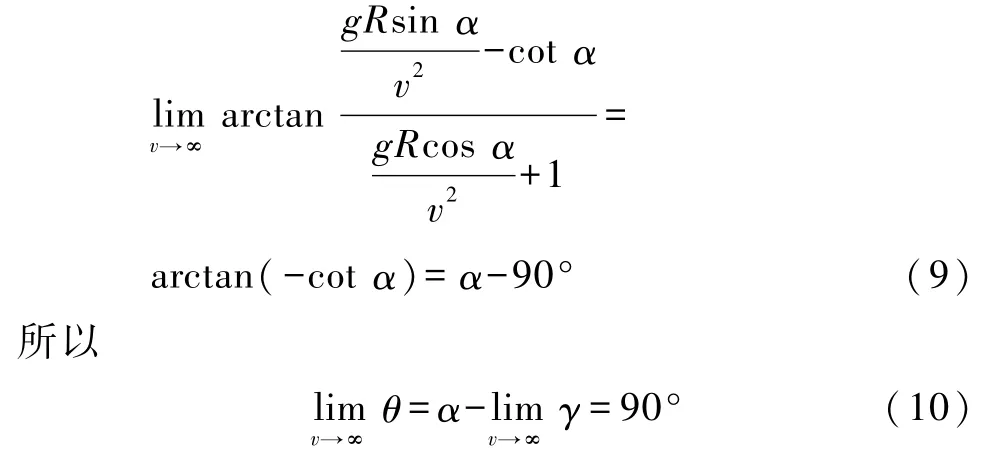
这说明，飞车在上半球轨道上运行时，速度越大，车身越接近于水平.

那么，α有没有一个最大值呢？即，轨道极限高度是多少呢？

由式（6）可知，当α＞90°时，要使该式有意义，必须保证cot α+μ0＞0，即

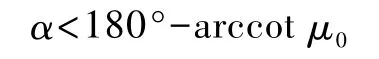
其物理意义是，当α＜180°-arccot μ0时，飞车能够做圆周运动，v有最小值.当α≥180°-arccot μ0时，不管飞车速度多大，都不能保持圆周运动.这就是飞车在上半球水平轨道运行的理论极限高度.

摩托车轮胎与铁笼粗糙的表面之间的静摩擦系数μ0一般为0.7左右，上式可以求出α最大理论值为124.99°［2］.此时，摩托车的允许最小速度由式（6）得出vmin→∞，倾角θ→90°.

当然，物体运动速度不可能无穷大，况且人体骨骼能够承受的最大压力为自身重量的3倍左右［2］.即

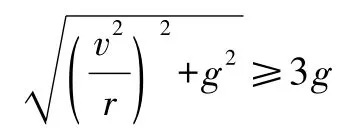
要使飞车在尽量高的水平轨道上运行，r要尽可能小.并且考虑车手身体的承受能力，v也要尽可能小.将v的最小值带入上式，可求出α的实际最大值为

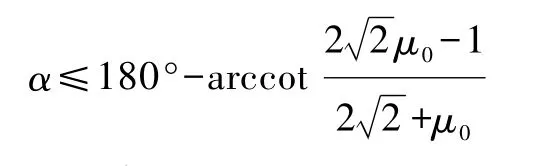
将μ0=0.7代入后求出

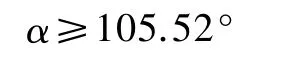
即水平轨道的最大高度α不能超过105.52°，摩托车允许的最小速度vmin≈9.316 m/s，折合时速约为33.54 km/h.此时车身倾角θ≈70.528°.在该轨道上，如果再增大车速，车手身体将无法承受.

通过以上分析可以看出，静摩擦力竖直分量的一部分抵消了自身重量，“环球飞车”是可以在球体上半球做水平圆周运动的.不过，任何水平轨道都存在一个速度的最小值，随着轨道的升高，允许的最小速度也在增大.当轨道上升到接近理论最大高度时，其允许的最小速度也上升到接近无穷大.

球内水平轨道的极限高度只与静摩擦系数μ0有关，与速度、球体大小均无关.如若摩托车运行的水平轨道超过理论极限高度，无论速度多大，都会打滑，发生危险.

［1］樊莉，孙慧.飞车走壁的力学分析［J］.大学物理，2012，32（7）：24-25.

［2］张怀华，石翔.探寻环球飞车表演的极限高度［J］.中学物理教学参考，2011（10）：28.

［3］刘延柱.飞车走壁的动力学［J］.力学与实践，2014（2）：246-248.

A dynamical analysis of global aerodyne

MIAO Ying-kai
（Puyang Vocational and Technical College，Puyang，Henan 457000，China）

This paper analyzes the mechanics of global aerodyne that does circular motion on the horizontal rail.Using forces and moments balance of the motorcycle in the movement，the stress situation，the maximum speed and the body inclination of the motorcycle doing circular motion in the horizontal rail are analyzed.The maximum height of the rail is calculated.

global aerodyne；circular motion；centroid motion theorem；rail height limit

O 312.1

A

1000-0712（2016）05-0005-03

2015-07-09；

2015-11-29

苗英恺（1972—），男，河南清丰县人，濮阳职业技术学院实训中心副教授，硕士，主要从事大学物理教学和研究工作.