关于《一维圆环上双原子链的马德隆常数》的解析解
2016-10-25韩玖荣
陈 贝,罗 强,韩玖荣
(1.扬州大学物理科学与技术学院,江苏扬州 225002;2.中国人民大学物理系,北京 100872)
关于《一维圆环上双原子链的马德隆常数》的解析解
陈 贝1,罗 强2,韩玖荣1
(1.扬州大学物理科学与技术学院,江苏扬州 225002;2.中国人民大学物理系,北京 100872)
在《大学物理》2015年第2期刊登的题为《一维圆环上双原子链的马德隆常数》一文的基础上,给出了针对原文中式(4)、式(11)和式(15)对应的解析形式,指出了原文中一个双伽马函数恒等式(8)的失误,同时也提出了二聚化情形下马德隆常数新的定义方式.
马德隆常数;双原子链;解析解
由于马德隆常数能反映晶体的静电势特征,对研究晶体结构提供很大的便利,所以从它被提出伊始便一直成为人们关注的焦点.马德隆常数的级数表示往往是条件收敛的,因此如何精确得到它的精确解并非是一件平淡无奇的事情.在过去的一个世纪里研究者们致力于不同空间维度(如一维、二维等)不同晶体结构(如NaCl、CsCl等)下马德隆常数计算方法的研究[1].
物理学中很多重要的物理量在一维(甚至只有一维)情况下是存在严格解的.量子力学中一维无限深方势阱、谐振子问题的能级和波函数在薛定谔(Schroedinger)方程下是精确可解的[2],统计物理中一维外场下经典伊辛(Ising)模型的配分函数可以由转移矩阵的方法给出[3],强关联物理中一维海森伯(Heisenberg)模型的基态能等可以通过Bethe方案解析地计算得到[4].马德隆常数亦是如此.在《大学物理》最近刊登的一篇题为《一维圆环上双原子链的马德隆常数》的文章里[5],其作者在计算一维马德隆(Madelung)常数上颇有新意,该文将一维链首尾相连组成一个圆环,据此给出了一维圆环上正负交替分布的离子晶体的马德隆常数的表达式,以及二聚化后的马德隆常数表达式.对于前者该文通过外推得知当原胞个数N趋于无穷时圆环上的马德隆常数趋于2ln2,并由此衍生出两个与双伽马函数ψ有关的恒等式;对于后者该文计算了某些特定取值下直线链和圆环上的马德隆常数,数值结果表明两者在5位有效数字精度内相等.
作为一种非常重要的补充,解析解往往能使得物理问题更加具有数学上的结构美.因此在《一维圆环上双原子链的马德隆常数》一文的基础上,本文给出了原文中式(4)、式(11)和式(15),分别对应于本文式(1)、式(4)和式(9)的解析形式.
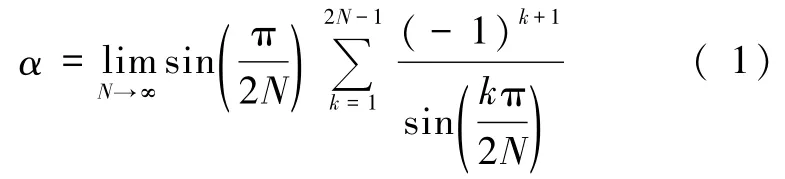
文献[5]利用正弦函数的级数形式并没有使式(1)得到简化,而采用积分等式[6,7]
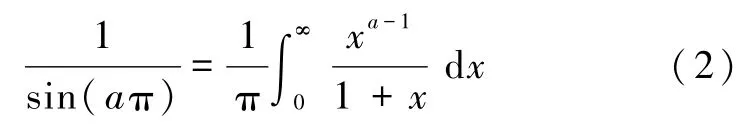
并运用几何级数的求和法则和控制收敛定理,可知
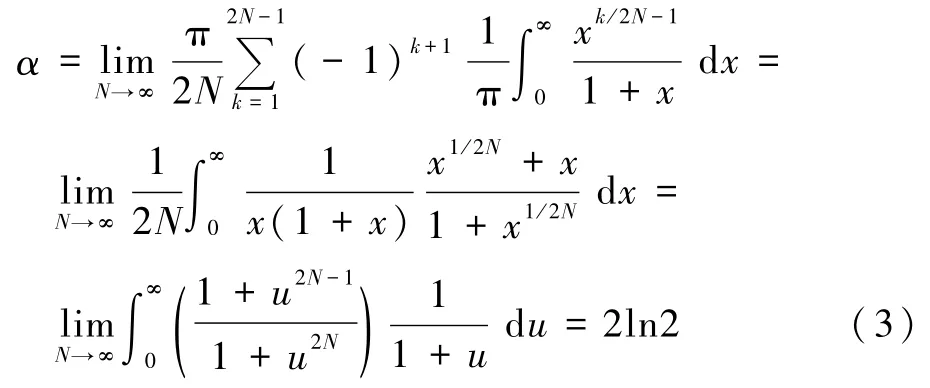
由此可知圆环上的马德隆常数和直线链上的马德隆常数在链长无限大时确实一致.
在正负离子二聚化情形下,离子晶体的马德隆常数通过表征二聚化程度的参数λ来调节.原文作者证明[1],在直线链情况下,马德隆常数可以表示成
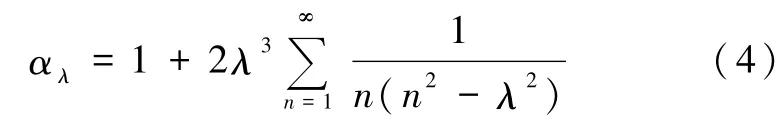
利用双伽马函数ψ的级数表达式[6]
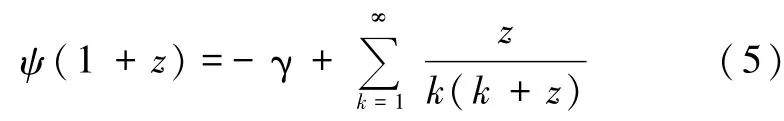
式中γ=0.577…表示欧拉(Euler)常数,可知
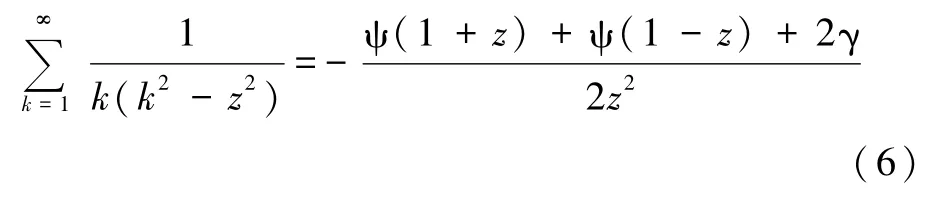
又由双伽马函数ψ的递推公式[6]
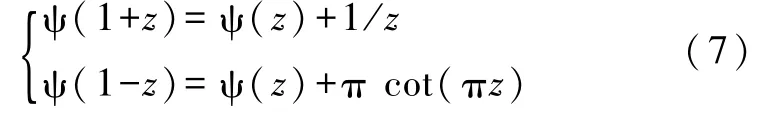
可得直线链下的马德隆常数
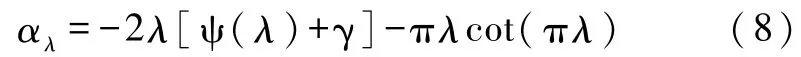
而在圆环下,马德隆常数可以表示成[5]
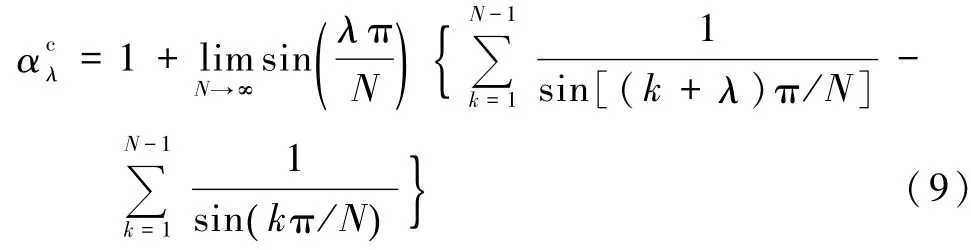
利用式(2),并运用同计算式(1)完全相同的方法可知

利用双伽马函数ψ的积分表示[6]
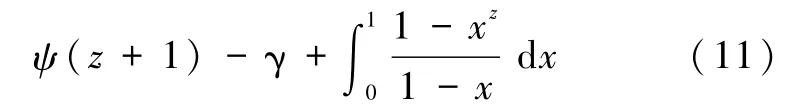
立即得到马德隆常数
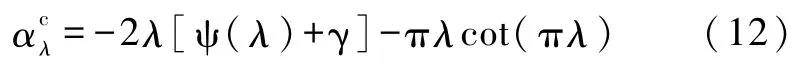
显然,式(8)和式(12)告诉我们,在一维二聚化情形下,直线链上和圆环上的马德隆常数确实一致,其函数图像如图1虚线所示.特别地,当λ=1/2时,α1/2=2ln2,这回归到一维NaCl型马德隆常数的情形.
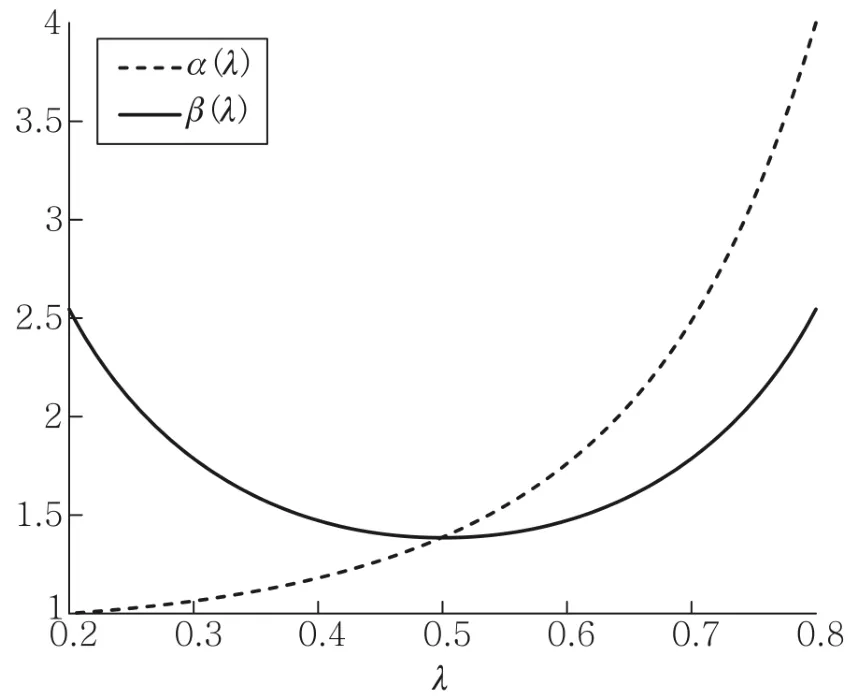
图1 二聚化情形下马德隆常数与参数λ的关系曲线
在计算圆环上的马德隆常数时,原文作者通过数值结果猜测出两个双伽马函数ψ恒等式,但原文式(8)
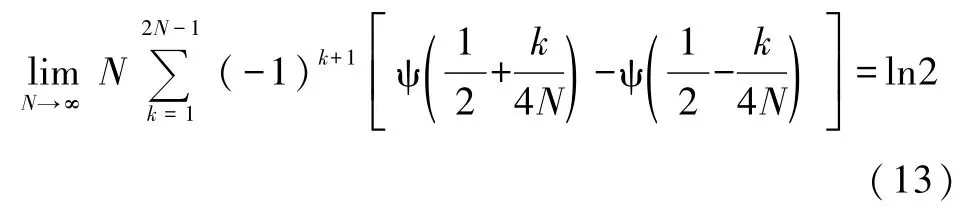
存在一些笔误,应该纠正为
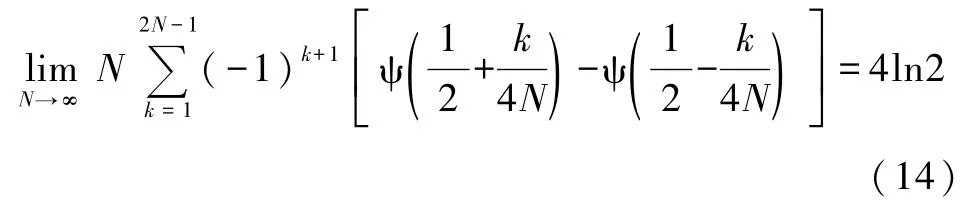
在正负离子二聚化情形下会存在正负离子间距不相等这一情况,原文作者给出的晶格能是以“短键长”(2λa和2μa分别表示链上和圆环上短键的长度)为长度尺寸的,其余无量纲常数则作为马德隆常数的定义.实际上,马德隆常数代表的是离子晶体晶格能中各离子间库仑能的总和,其大小要与晶体的几何构型,如维度、配位数等一致,因此其定义式要尽可能地囊括所有的结构参数以利于晶体能的计算[8,9].不难验证,在二聚化情形下晶格能具有对称性Uλ=U1-λ(0<λ<1),而原作者给出的马德隆常数αλ显然不具备这种对称性.此外,作者给出的晶格能中包含了“键长”(原文定义式的分母2λa和2μa分别表示链上和圆环上短键的长度)的概念,而在圆环上短键和长键之和并不等于原胞间距,此时“键长”并非是一个直观的物理量.因此,为了体现晶格能具有的对称性同时也为了计算的方便,我们建议把库仑势分母上的二聚化参数λ吸收到马德隆常数的定义中.我们给出的修正方案是
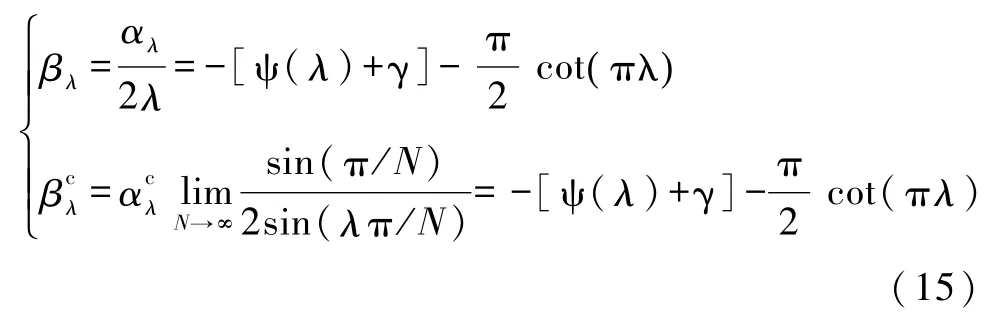
式中二聚化参数λ定义为原胞内正负离子间距与原胞间距的比值(链情形),或者原胞内正负离子间夹角与原胞间夹角的比值(圆环情形).修正后的马德隆常数如图1实线所示.此时,链上和圆环上的晶格能可以统一地写成,形式上更加简洁明了,功效上一旦给定马德隆常数则不需要额外的数学处理就可以立即知道晶格能的大小.
综上所述,本文完善了徐宝等人给出圆环上马德隆常数式(4)以及二聚化情形下马德隆常数式式(11)和式(15)的解析形式,同时也提出了二聚化情形下马德隆常数新的定义以便修正后的马德隆常数更能全面反映晶体静电势的对称性特征.
后记:在本文审稿期间,我们发现邱为钢老师也做了类似工作[10].
[1]Borwein D,Borwein J M,Taylor K F.Convergence of lattice sums and Madelung’s constant[J].Journal of Mathematical Physics,1985,26(11):2999-3009.
[2]周世勋.量子力学教程[M].2版.高等教育出版社,2009:26-34.
[3]杨展如.量子统计物理学[M].高等教育出版社,2007:147-150.
[4]Sutherland B.Beautiful models:70 years of exactly solved quantum many-body problems[M].World Scientific Publishing Co Ptc Ltd,2004:143-161.
[5]徐宝,吴洪业,赵建军,等.一维圆环上双原子链的马德隆常数[J].大学物理,2015,34(2):41-42.
[6]王竹溪,郭敦仁.特殊函数概论[M].北京:北京大学出版社,2012:69-83.
[7]梁昆淼.数学物理方法[M].刘法、廖国庆,修订.4版.北京:高等教育出版社,2010:64.
[8]黄昆.固体物理学[M].北京:北京大学出版社,2009:37-41.
[9]Pereira P C N,Apolinario S W S.Madelung energy of Yukawa lattices[J].Physical Review E,2012,86(4):046702.
[10]邱为钢.无穷求和与渐进展开[J].大学物理,2015,34(10):23-24.
Analytical solutions of Madelung constant of double atomic chain on circles
CHEN Bei1,LUO Qiang2,HAN Jiu-rong1
(1.School of Physical Science and Technology,Yangzhou University,Yangzhou,Jiangsu 225002,China;2.Department of Physics,Renmin University of China,Beijing 100872,China)
We give the analytical solutions of all the remaining expressions(the original equations(4),(11)and(15))and correct the identity of the digamma function(the original equation(8)),and propose a new definition of the Madelung constant in the situation of dimerization in a recent paper titled《Madelung constant of double atomic chain on circles in college physics》.
Madelung constant;double atomic chain;Analytical solution
O 481
A
1000-0712(2016)05-0050-03
2015-08-25;
2015-12-21
陈贝(1993—),女,江苏南京人,扬州大学物理科学与技术学院2012级本科生.
