稳态平板法测液体导热系数的分析

安艳伟，谢 亮

（北方工业大学理学院，北京 100144）

稳态平板法测液体导热系数的分析

安艳伟，谢 亮

（北方工业大学理学院，北京 100144）

用稳态平板法测定了不同温度下液体的导热系数.对冷却速率的计算分别采用线性拟合、逐差法等6种方法；并计算出了相应的导热系数.最终的导热系数计算结果表明，在冷却速率的6种计算方法中，线性拟合效果比较好.

稳态平板法；液体；冷却速率；导热系数

导热系数是表征材料导热性能的一个重要参数，它不仅是评价材料热学特性的依据，也是材料在设计应用时的一个依据.熔炼炉、传热管道、散热器、加热器，以及日常生活中水瓶、冰箱等都要考虑它们的导热程度大小，所以对导热系数的研究与测量显得很有必要，导热系数不仅与温度和压力有关，还与材料本身的性质、结构有关，因此确定大多数材料的导热系数都要用实验法确定.测量导热系数的方法主要为稳态法和非稳态法，前者主要有平板法，后者主要有瞬态热丝法、热线法和探针法等.基于稳态平板法导热系数测定仪的成本较低，被高校、科研单位和企业广为采用.对导热性能差的材料或隔热材料的导热系数的测定，稳态平板法是最为理想而准确的方法之一［1］.

目前，各高校测量导热系数的实验多以固体为测试样品.对于液体，由于导热系数较小，基本属于不良导热体，而且液体具有流动性，特别是在加热时，液体内因温差而形成的对流将使其导热系数的准确性降低.有的文献介绍了一种稳态圆筒法测水的导热系数［2］，温度范围只在0℃到室温的比较低范围内.有的文献介绍了用对比法测液体的导热系数［3］，需要在导热系数已知的标准溶液作对比的条件下进行.目前水在不同温度下的导热系数基本已知，但是还没有用稳态平板法对水的导热系数进行测定.本文作者自制测试液体样品盘，用稳态平板法对水的导热系数进行了测试研究，对稳态值的确定采用了重复测量的方法；对冷却速率的确定分别采用了线性拟合、逐差法等6种计算方法，并计算出了相应的导热系数.通过对比分析，给出了最佳方案.

1 实验原理

1.1 导热系数测量理论

1882年法国科学家傅里叶建立了热传导理论.当材料内部有温度梯度存在时，就有热量从高温处传向低温处，单位时间内通过单位面积的热量正比于物体内的温度梯度，其比例系数即为材料的导热系数.用公式表示为

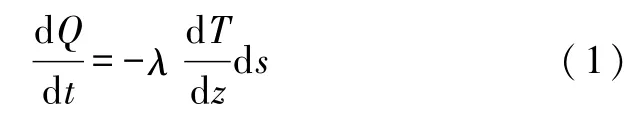
式（1）中，dQ/dt为传热速率，负号表示热量从高温处向低温处传递，λ为材料的导热系数，dT/dz为与面积ds垂直方向上的温度梯度.

1.2 稳态平板法测量原理

如图1所示，热流由上向下传导，当平板热传导系统达到稳态时，加热盘A在样品B内部形成一个稳定的温度分布，若忽略样品的侧面散热，可认为样品盘B的传热速率等于散热盘P的散热速率.

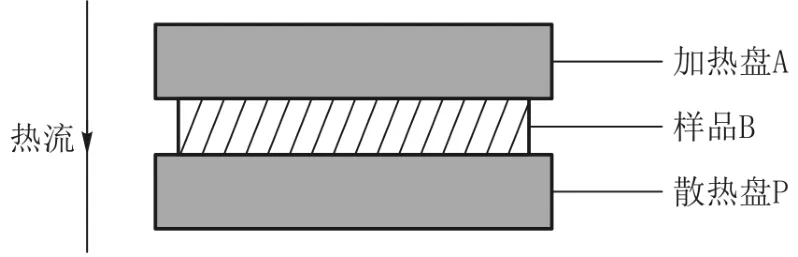
图1 热传导示意图

若样品B的厚度为h、表面积为s，其上下表面的温度分别为T1、T2，则dt时间内沿面积s垂直方向所传递的热量满足傅立叶热传导公式，由式（1）可知，样品B的传热速率为

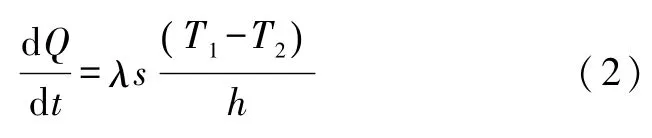
散热盘P在温度为T2时的散热速率为

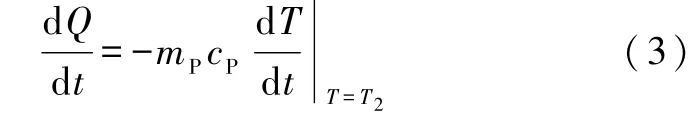
实验中散热盘P冷却速率的测量方法是，测出稳态时样品上下表面的温度T1、T2后，将样品B撤去，让加热盘A与散热盘P接触，当散热盘的温度上升到比T2高出一定的范围后，移开加热盘，每隔30 s记录散热盘温度随时间的变化情况，求出散热盘在T2时的冷却速率（dT/dt）|T=T2.

由于冷却速率与散热面积成正比，在散热盘P散热速率的测量时，散热面为上、下表面与侧面，而在稳态散热时，散热盘P的上表面中面积为是被水盘覆盖的，故对散热速率公式加以修正，修正后散热盘P的散热速率为

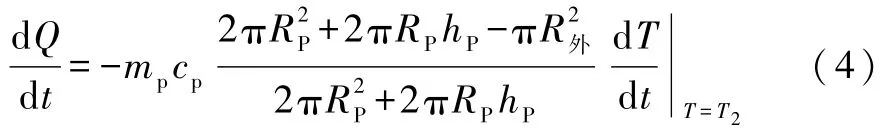
由式（2）、式（4）可得到导热系数表达式：

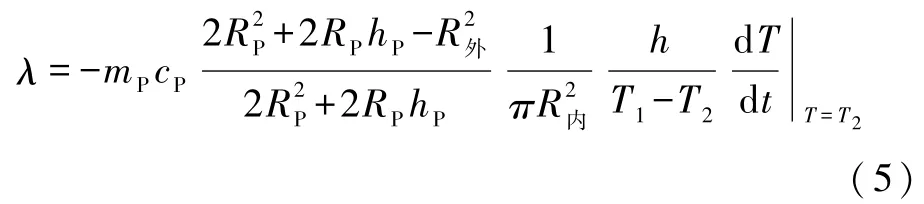
其中mP、cP、RP、hP分别为散热盘的质量、比热容、半径、厚度，R内、R外、h分别为样品盘的内、外半径、深度.由式（5）可知，在散热盘、测试样品固定不变的条件下，温差和冷却速率的误差大小是决定导热系数误差大小的两个主要因素.

2 实验器材与实验技巧

本实验使用YBF-2型导热系数测试仪，选用铜-康铜热电偶测温度，温差100℃时，其温差电势（以下简称电压）约为4.27 mV，该仪器配有量程0～20 mV，并能读到0.01 mV的数字电压表（数字电压表前端采用自稳零放大器，故无须调零）.导热系数计算式（5）中含有，在温差不太大时电压与温度的比值为常量，因此，计算时无须把电压值转换为温度值，直接代入电压值即可，可以减少由于转换引入的误差.

测试用水盘的制作：平板法测不良热导体的导热系数时，仪器说明书和一些文献所提供的样品厚度在10 mm左右［4-6］，本文选用外径为126.00 mm内径为119.00 mm，宽度9.20 mm的硬质聚氨酯泡沫塑料圆环（导热系数0.019～0.030 w/m·K，从而减少侧面散热），环两边用砂纸打磨平整，上外沿添加密封圈，下沿用AB胶粘在厚度为0.20 mm与其直径相同的圆铜片上（根据复合材料导热系数测定［7］可知，铜片的影响忽略不计），如图2所示，圆环上粘接两个内径为0.80 mm的排水管，以供水被加热后膨胀时排出.

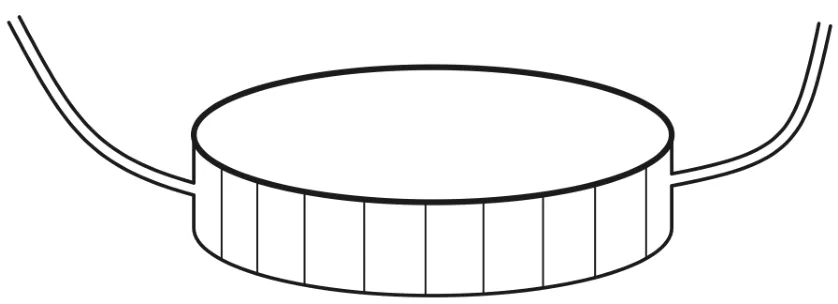
图2 水盘示意图

实验过程中为减小实验误差所做的处理：

1）减小热阻方法：热传导过程中由于接触表面不光滑，进而有微小空气泡产生热阻，实验时可以在接触面上涂上膏体［8-9］、油状物［10］或液体驱赶走空气泡.本实验中在上、下铜盘之间涂一层水，上、下铜盘的电压差值为0 mV，说明水在热传导过程中热阻可以忽略.

2）热电偶温度计探头处理：上、下铜盘上留有深至圆心的小孔来放置热电偶温度计探头.实验采用在探头上涂抹硅脂并用橡皮泥封住小孔口，以减小接触不良和小孔中空气对温度的影响.

3）散热方式的选择：通过实验发现采用对流散热方式，对上下盘的电压造成明显的波动性，而采用自然对流散热方式［11］上下盘的电压比较稳定，因此，本实验采用自然对流散热方式散热.

3 实验结果与分析

3.1 稳态值的测定

本实验对设定加热盘A的温度选择也有一定的局限性，最低温度一般应高于环境温度15℃左右，最高温度不能超过80℃，否则，温度太高水中容易产生气泡和对流影响水的热传导.水在不同温度下导热系数不同，实验选择低、中、高3个温度作为代表，将加热盘的温度分别设定为45.0℃、55.0℃、65.0℃，达到稳态时（10 min内电压基本不变），记录A盘和P盘的电压值，实验完毕更换水重复测试，每一个设定温度重复5次.结果见表1.

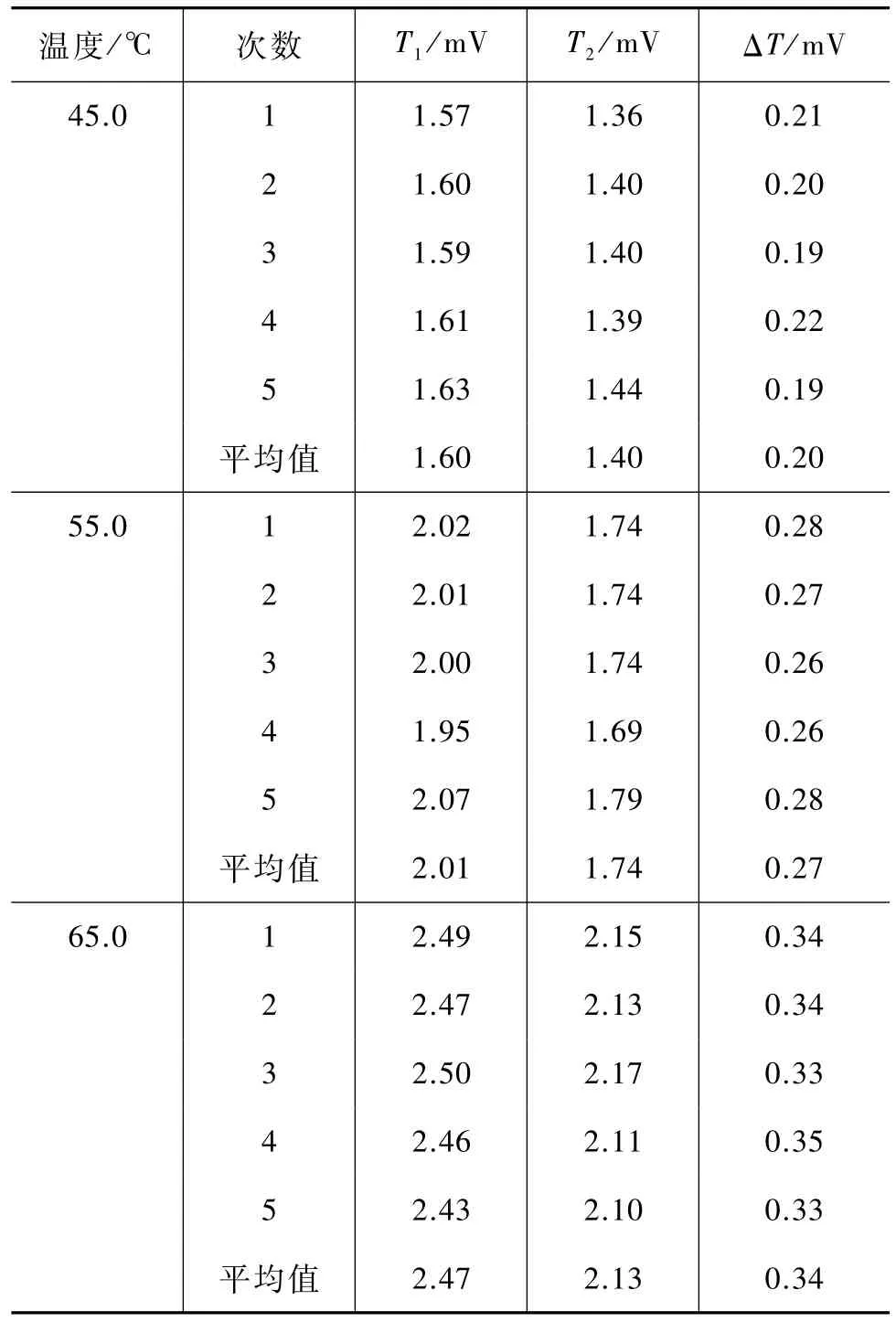
表1 稳态时A盘和P盘温度所对应的电压值室温：（25.0±0.5）℃

对表1的数据分析可知，在环境温度和设定加热盘温度相同的条件下测试，样品上下表面的电压值并非固定不变而是略有起伏，其原因与环境温度的起伏、测试时间长短、热电偶冷端的温度、水盘中水量的差别等因素有关.我们近似认为设定的3个温度下的5次测量属于等精度测量，取各自平均值作为其稳态时样品上下表面的电压值.

3.2 冷却速率的测定

散热时，散热盘采用自然对流散热的方式，对电压值在2.50～1.20 mV范围的冷却过程进行测试，每隔30 s记录散热盘电压随时间的变化情况，作T-t冷却曲线，如图3所示.

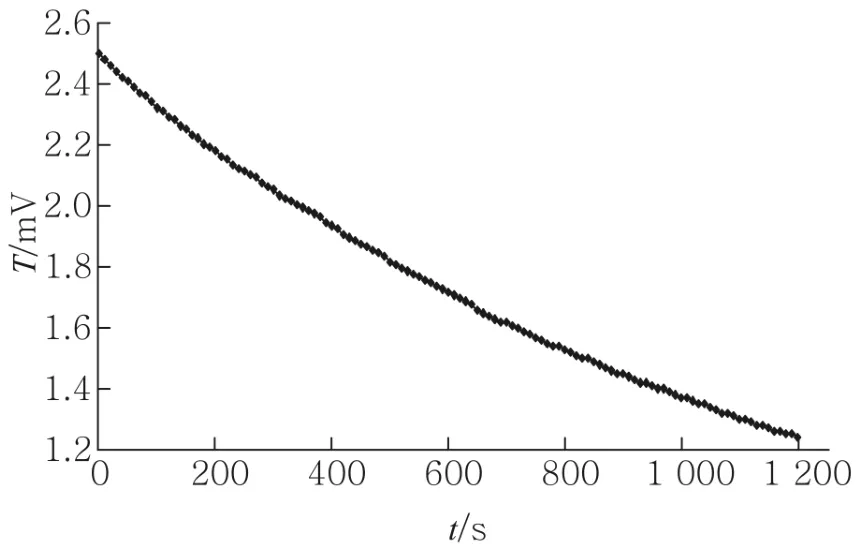
图3 散热盘冷却数据分布

求解每个设定温度下的冷却速率时，选取的冷却数据范围是从高于稳态时T2数值的0.2 mV左右至低于稳态时T2数值的0.2 mV左右为止.

有关冷却速率的求解方法有的文献采用了线性拟合［12］，有的文献采用了多项式拟合［13-15］，有的文献采用了指数拟合［4，16］.本文分别对45.0℃、55.0℃、65.0℃的冷却曲线进行3种曲线拟合：二阶多项式拟合、线性拟合和指数拟合，进一步得到冷却速率；又分别用近似法、逐差法和镜尺作图法得到冷却速率，总共6种方法得到的冷却速率结果见表2.

表2 冷却速率

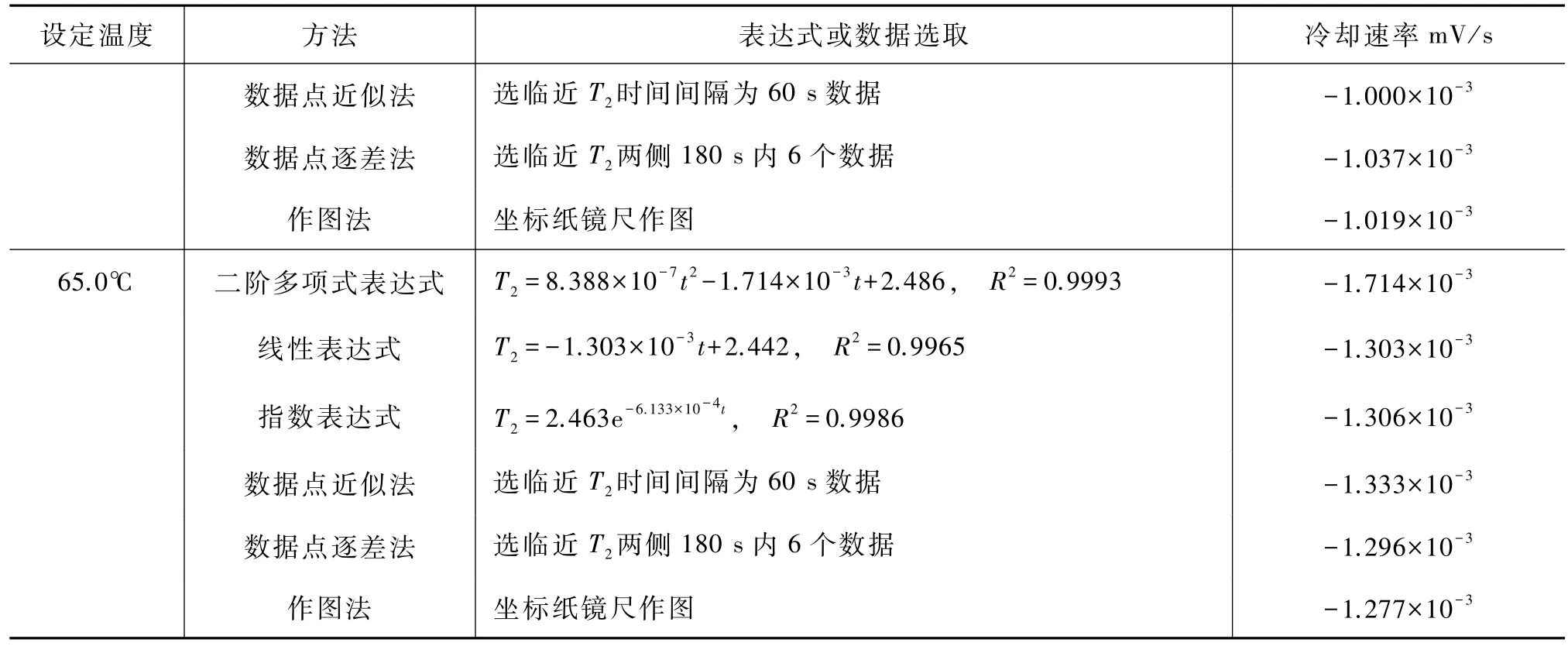
续表

由表2可知：对测试数据分别采用二阶多项式曲线拟合，线性表达式拟合和指数拟合，由相关系数说明各种拟合曲线与所对应表达式相符.3个温度下由多项式拟合所得冷却速率都偏大，另外5种方法所得冷却速率相差不大.

3.3 导热系数的计算

通过查铜-康铜热电偶分度表得到电压所对应的温度值；不同温度下水导热系数通过查阅资料得到.把查阅资料得到的水在相应温度下的导热系数当作理论值.具体数据见表3.

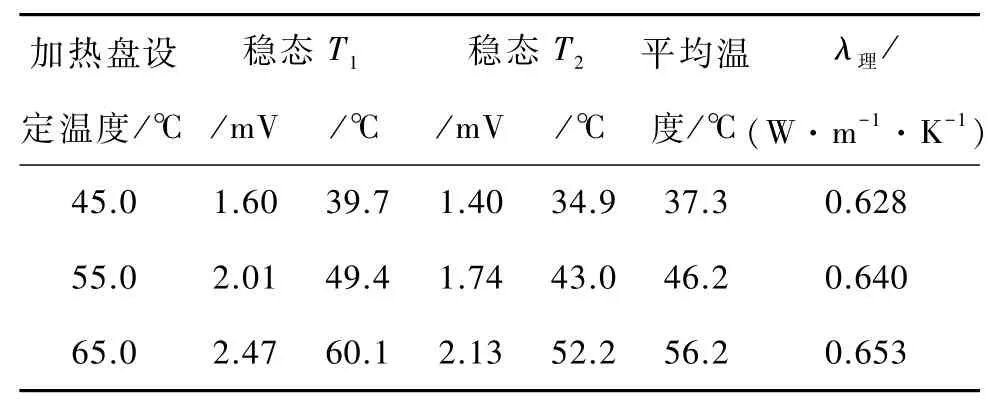
表3 水的温度及对应导热系数

实验中测得散热盘P的质量、直径和厚度的平均值分别为：mP=857 g，DP=130.00 mm，hP= 7.00 mm；水盘的内、外直径和深度的平均值分别为：D内=118.60 mm，D外=121.40 mm，h=9.20 mm.散热盘P的比热容为c=385 J/K·kg.将以上数据及稳态数据、冷却速率数据代人式（5）计算得到导热系数.把采用各种方法计算得到的导热系数与表3中所对应的导热系数相比得到相对误差，计算结果见表4.

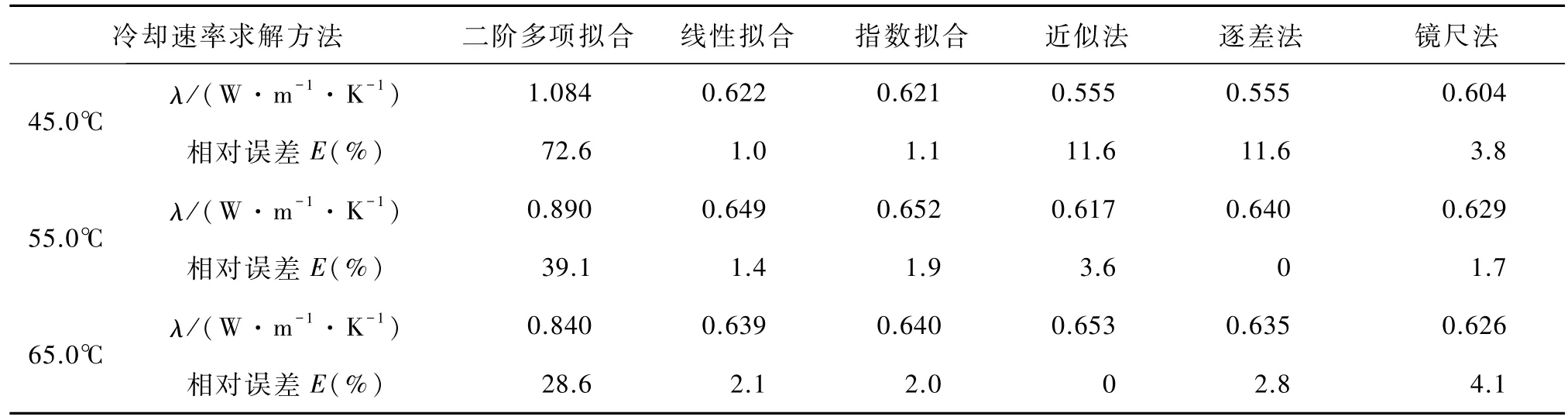
表4 导热系数

由表4可知，二阶多项拟合所得到的导热系数误差最大，实验中不宜使用.从3个温度对比来说，近似法、逐差法和镜尺法存在一定的随机性，例如在45.0℃条件下，逐差法和近似法误差比较大都超过5%，而在55.0℃条件下，逐差法误差最小，在65.0℃条件下，近似法误差最小.线性拟合和指数拟合相对误差结果比较接近，相对而言误差比较小.由于利用计算机软件处理数据，可减少人为因素引入的误差，因此，从简单直接、误差小方面考虑，用线性拟合求解冷却速率是比较好的方法.

3.4 不确定度分析

导热系数不确定度主要由稳态温差值和冷却速率两方面引入，现以常用的逐差法和线性拟合法为例分别估算不确定度.数字电压表的读数不确定度为0.01 mV，所以稳态电压值的不确定度均取0.01 mV，以常用的逐差法和线性拟合法为例估算结果见表5.从表5不确定度大小来看，线性拟合优于逐差法.

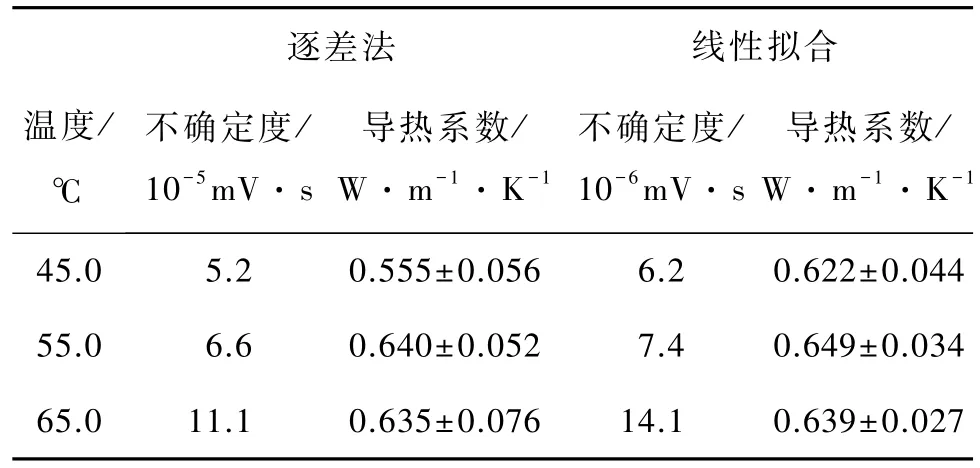
表5 逐差法和线性拟合法结果

4 结语

稳态温差值和冷却速率值的误差大小是影响导热系数误差大小的两个主要因素.通过用稳态平板法对水的导热系数测试研究发现，在重复稳态测量时，即使设定加热盘和环境温度不变，稳态所对应的样品上下表面的电压也有起伏，由于其差值比较小，其值的微小变化会对结果造成比较大的影响，因此，作者用多次测量的方法，来保证稳态值的准确性.目前，文献报导的稳态测量都是单次测量，其样品上下表面的温差值相对比较大，而对于温差比较小，采用多次稳态测量的还没有文献报导.对于冷却速率的计算，本文采用了6种方法，最终的导热系数计算结果表明，线性拟合法比较好，因此，在冷却速率的计算时，作者建议多用几种方法进行对比分析.不足之处是，使用YBF-2型导热系数测试仪，其电压表分辨率为0.01 mV，若设定加热盘温度太低，其稳态值所对应的上、下盘的电压值比较小，相对而言，仪器误差所占比例比较大；若设定加热盘温度太高，样品水内容易产生气泡和对流，因此，最合理的温度有待进一步实验研究.

［1］唐运林，朱肖平.新编大学物理实验［M］.重庆：重庆大学出版社，2004：46-48.

［2］李成仁，吕翎，曲业民，等.液体导热系数的测量［J］.物理实验，1993，14（3）：105-106.

［3］周其云.溶液导热系数测定仪的研制［J］.实验室研究与探索，1996，3：60-63.

［4］刘艳峰.泡沫塑料导热系数随温度变化规律的研究［J］.河南科学，2015，33（2）：160-163.

［5］金忆凡，吉唯峰，乔卫平，等.“稳态对比法”测量不良导体的导热系数［J］.物理实验，2012，32（1）：44-45.

［6］林琦，曹立翔，周威.水立方薄膜（ETFE膜）导热系数的测定［J］.实验科学与技术2011，9（5）：60-61，64.

［7］陈则韶，钱军，叶一火.复合材料等效导热系数的理论推算［J］.中国科学技术大学学报，1992，22（4）：416-424.

［8］冉凯华，冷雪松，王艳东.测量不良导体导热系数实验装置的改进［J］.实验室研究与探索，2013，32（9）：47-50.

［9］王国庆，朱冬生，林琳.吸附剂之间及其与铜表面之间的传热强化研究［J］.化学工程，1999，27（6）：13-15.

［10］李灵杰.带孔片状不良导体导热系数测试方法探究［J］.大学物理实验，2011，24（2）：59-61.

［11］官邦贵，秦炎福，王玉连，等.不良导体导热系数测量实验中两种冷却方式的对比研究［J］.物理与工程，2009，19（5）：45-46，63.

［12］舒晓玲，池荟，竺江峰.固体热导率测量仪的新发现［J］.大学物理实验，2013，26（5）：25-28.

［13］侯瑞宁，罗道斌，王虹.稳态法测导热系数的数据处理方法［J］.广西物理，2009，30（2）：45-47.

［14］魏永生，于晓东，李保民，等.用Mathematica处理和分析实验数据［J］.实验室研究与探索，2005，24（6）：62-64，87.

［15］易志俊，陈伟，李娜，等.基于DISLab温度传感器的导热系数测定［J］.大学物理实验，2014，27（4）：94-96.

［16］陆泽璇，张军朋.用Origin处理导热系数测定实验的数据［J］.大学物理实验，2013，26（6）：101-104.

Analysis on using stable plate method to measure the thermal conductivity of liquid

AN Yan-wei，XIE Liang
（College of Science，North China University of Technology，Beijing 100144，China）

The thermal conductivity of liquid at different temperatures has been measured by using the stableplate method.Six methods such as linear fitting，progressive difference and so on，are used in the calculation of cooling rate.Meanwhile，the corresponding thermal conductivity coefficients have been calculated.The final thermal conductivity calculation results show that the result given by linear fitting among the six different ways is the best.

stable plate method；liquid；cooling rate；thermal conductivity

O 551

A

1000-0712（2016）05-0019-05

2015-08-09；

2015-11-15

安艳伟（1969—），女，河北正定人，北方工业大学实验师，主要从事大学物理实验的教学与研究工作.