平面波作用下两种声强阵列的精度对比和数值分析*

王红卫　张龙

(1.华南理工大学 建筑学院，广东 广州 510640；2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640)



平面波作用下两种声强阵列的精度对比和数值分析*

王红卫1,2张龙1

(1.华南理工大学 建筑学院，广东 广州 510640；2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640)

从平面波作用下三维声强阵列的理论推导出发，通过声压、质点振速估计和声强谱计算，比较了正四面体传声器和六传声器的幅值误差和方向性误差，并在全消声室中对数值仿真的结果进行验证.研究结果表明：随着频率增加，幅值误差呈指数式增长，4 kHz范围内两种传声器的幅值误差均小于0.5 dB，满足精度要求，且正四面体传声器略优于六传声器；在平面波作用下正四面体传声器的方向性精度明显优于六传声器，当频率为8 kHz时六传声器的角度偏差已接近6°，而正四面体传声器角度偏差仅为1°，且全频域范围内角度偏差增长缓慢.

平面波；三维声强；传声器；声压；数值仿真；幅值误差；方向性误差

平面声波对于现代声学测量和仿真技术具有不可替代的理论意义.当接收点与声源足够远时，波阵面即可近似为平面，因此平面声波理论可用于远离声源情况的分析和测试.三维声强传声器阵列基于传统的双传声器法，通过快速傅里叶变换求出每对传声器之间的互谱Gij，进而确定中心位置的声强，在声功率测量、噪声源定位等方面应用较为广泛[1-3].文中分析了平面声波作用下三维传声器阵列的幅值和角度误差，有助于从理论上改进三维声强探头的生产工艺，进而提升其性能和测量的精确度.

文献[4]提出了一种基于有限差分的系统性误差计算方法，并将它应用于不同形式的传声器阵列以此来验证其有效性；文献[5]比较分析了球面声波作用下3种传声器阵列的能量密度和声强幅值随ka(波数和间距的乘积)的变化特性，并考虑了存在钢球散射作用时的精度差异；文献[6]则从一维声强探头的原理入手，以类比的方式提出了在高频范围内三维声强探头敏感性缺失的补偿策略，并通过数值计算验证了当存在相位匹配误差和界面反射的情况时，这种补偿策略依然适用；文献[7-8]虽给出了在平面声波作用下四传声器的幅值误差和相应的误差修正方案，但仿真的边界条件仍局限于入射声波方向取某个具体角度，以此来推测整个球面空间内的误差情况，由于模拟的样本数量有限因而不具有一般性.本研究则在理论推导和数值模拟的基础上比较了空间笛卡尔坐标系下1/8卦限内，入射角以10°为步长规则增加时幅值误差和方向性误差随频率f的变化情况，并结合实验数据予以分析验证.

1　平面波作用下三维声强的理论推导

相对于传统的声压法，三维声强阵列是通过空间中若干个点的声压值来推算几何中心位置的声压值和质点振动速度，最后代入相应定义求得声强.

1.1三维声强阵列的传声器布置

传声器阵列的空间布置方式与系统的有限差分误差密切相关.常见的布置方式有正四面体传声器阵列(简称四传声器)和六传声器阵列(简称六传声器)，文中分别比较了两个不同测试系统中心位置的声强，分析了这两种三维声强探头的误差及影响因素，其空间笛卡尔坐标系下的传声器分布如图1所示.

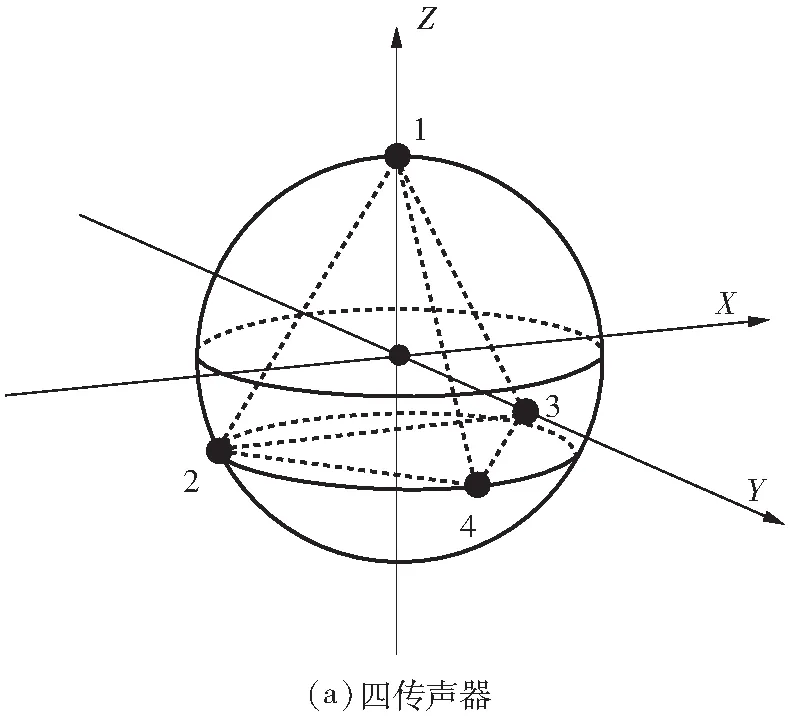
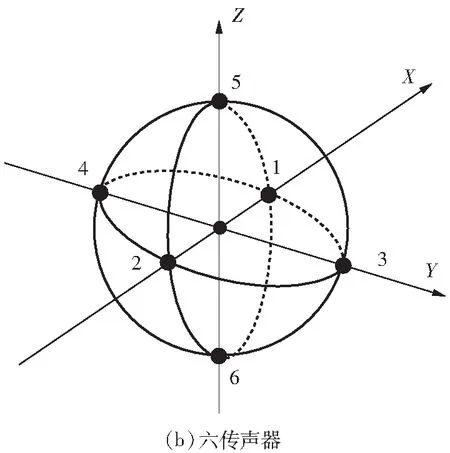
图1　传声器布置方式及坐标系统

假设球体的半径为R，所有传声器均分布在球面上，由于空间的对称性，两种布置方式球心与坐标原点均重合，根据几何关系可以推得各传声器的空间坐标，如表1、2所示.

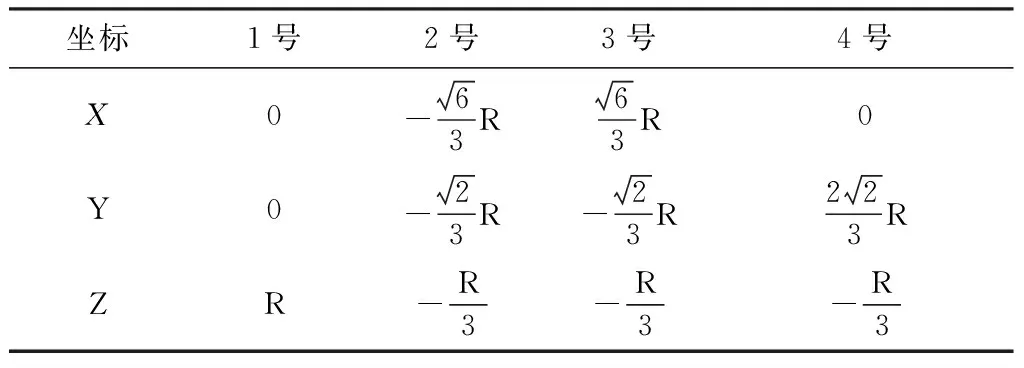
表1　四传声器阵列空间坐标Table 1　The space coordinates system of tetrahedral microphones

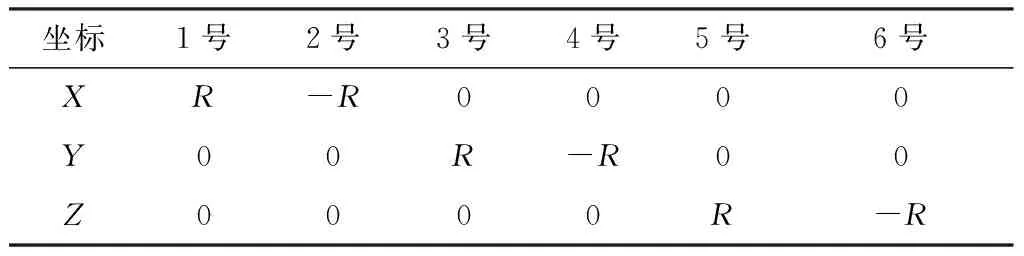
表2　六传声器阵列空间坐标

1.2声压估计

目前常用的三维声强阵列声压估计方法包括：取各点的算数平均值计算声压；几何中心额外增加虚拟传声器求得声压；加权平均值估计声压；泰勒公式展开估计声压等[6].这几种方法各有优点且适用范围不同，综合考虑上述几种估计方法的适用性及建立坐标系的方式后，文中声压估计采用式(1)所述的求算数平均值的方式.

(1)

式中，m表示某种布置方式的传声器个数，pi为各传声器位置的声压值.

1.3质点振速估计

质点振速在频域中可以表示为

Vi=(P2-P1)/j2πfρd

(2)

式中，P1、P2为每对传声器的声压，Vi表示沿1、2号传声器连线方向的质点振速，j为虚数单位，ρ表示空气密度，d为两传声器的间距.

结合传声器的空间坐标，可以得到VX、VY、VZ和各传声器声压之间的关系.

正四面体传声器声速估计：

(3)

六传声器声速估计：

(4)

1.4三维声强谱计算

由两信号的互相关函数可知[9]：

RPV())d

(5)

其中，RPV()表示声压和质点振速的互相关函数，p(·)和u(·)分别为声压和质点振速关于频率的函数.

类比于一维p-p探头声强与互谱的关系，可得到正四面体传声器几何中心位置声强谱分量：

(6)

六传声器声强谱分量：

(7)

式中，f为频率，Gij表示第i、j号传声器之间的单边互谱，Im表示取相关函数的虚部.

2　平面波作用下的误差分析

三维声强测试系统的误差包括有限差分误差和相位失配误差.有限差分误差主要是由于利用各点的声压估计中心位置的声压，且质点振速线性化过程中忽略了二阶及以上的无穷小.相位失配误差则是由于各个测量通道之间相位不匹配引起的.有限差分误差决定了频率的上限，且随着间距d增大高频误差增大；相位失配误差决定了频率的下限，且随着间距d减小低频误差增大.

文中采用Matlab对平面声波作用下的两种三维声强测试系统的有限差分误差进行仿真和数值计算.若系统不存在相位失配的情况，有限差分误差则表现为幅值、方向性与理论值的偏差.初始条件假定空气密度为1.21 kg/m3，声速为340 m/s，外接球半径为36.7 mm.入射波方向向量在XY平面上的投影与X轴夹角为φ，方向向量与Z轴夹角为θ，φ和θ的取值即决定了入射平面波的方向.XZ平面上φ、θ与坐标轴的关系如图2所示.

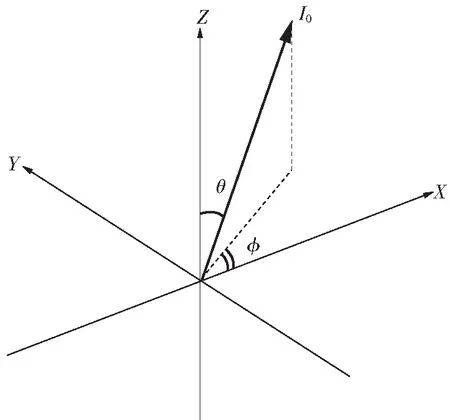
图2　平面波入射方向角度示意图

假设φ和θ均以0°为起始点，以10°为步长逐渐增加到90°.分别计算每一种入射方式下几何中心位置处的声强估计值，确定所有入射方式下估计值和理论值的平均相对误差，并对最终结果进行归一化处理.

2.1幅值误差比较与分析

幅值误差的理论计算公式如下：

(8)

(9)

式中：E为幅值误差大小；I表示正四面体传声器或六传声器几何中心位置的幅值估计值，此值可通过定义传声器阵列的空间分布从而计算声强谱得到；IA则为该入射方式下声强的给定值.

图3为在平面波作用下，正四面体传声器和六传声器的幅值误差随频率的变化情况，此数据是基于多种入射方式的统计分析结果.

由图3可以看出，随着频率f的增加，幅值误差呈指数关系增长.在f<1 kHz的频段内，两者相差不大，均小于0.1 dB；而当f>1 kHz时，正四面体传声器的幅值误差小于六传声器，4 kHz时，正四面体传声器幅值误差仅为0.25 dB，在可听频域范围内具备较高的精度.从图中还可以看出，高频段内正四面体传声器的幅值误差增长速度小于六传声器，6 kHz时两者差值为0.4 dB，而到10 kHz时差值则增加到0.9 dB.这一方面来源于系统的有限差分误差，由于每对传声器的距离d与幅值误差呈正相关，当外接球半径一定时，六传声器的有效频率上限小于四传声器；另一方面，六传声器若考虑除沿轴3对传声器外的其余12种组合，平均幅值误差及误差最大值均有不同程度的下降.上述结果与文献[10-11]结论相互印证.

图3　不同传声器的幅值误差随频率的变化

Fig.3The magnitude bias between different probes as frequency increases

为了进一步分析传声器摆放位置对误差的影响，分别计算沿X、Y、Z轴的幅值误差，计算公式如下[12-13]：

(10)

式中,EX、EY、EZ为声强估计值沿X、Y、Z轴方向的幅值误差分量，IA，X、IA，Y、IA，Z为声强给定值沿X、Y、Z轴方向的幅值误差分量.

平面波作用下两种传声器阵列沿X、Y、Z轴的幅值误差如图4所示.

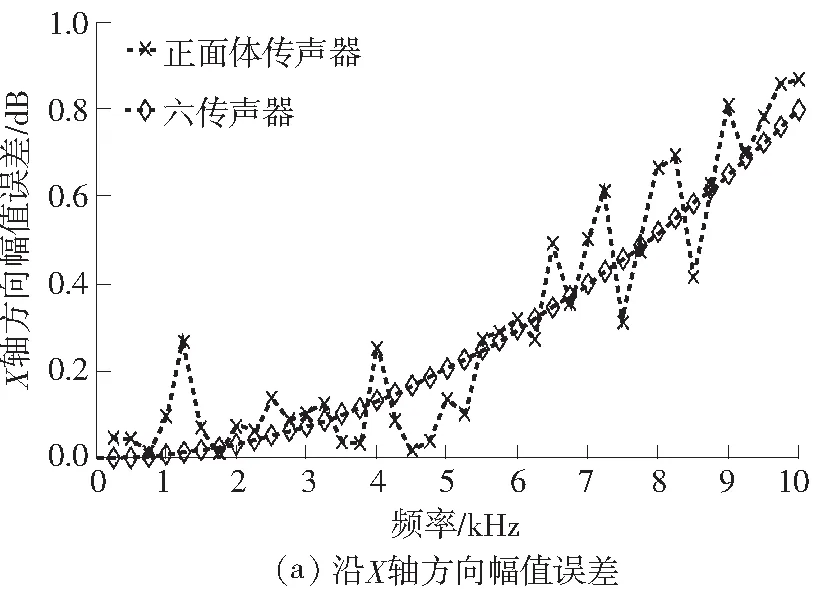
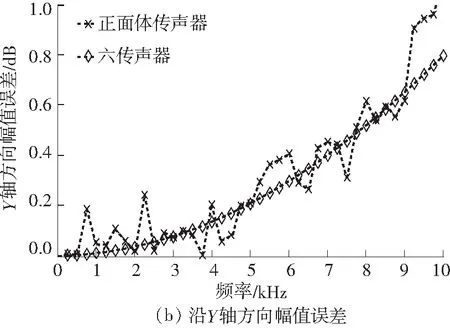
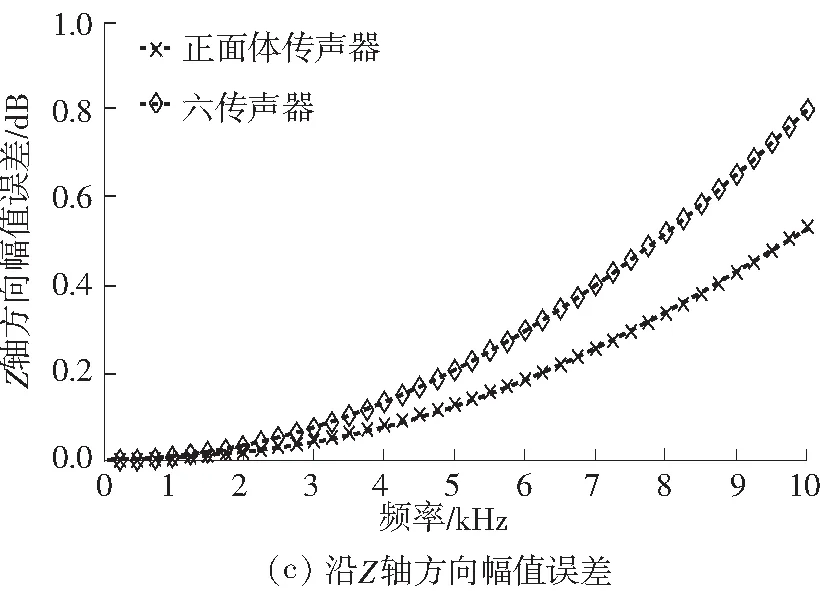
图4　沿不同坐标轴方向的幅值误差

由图4可见，当f>2.5 kHz 时，沿X、Y轴方向两者曲线上升趋势基本吻合，误差相差不大；当f<2.5 kHz时，沿X、Y轴方向正四面体传声器幅值误差略大于六传声器，最大误差小于0.4 dB；而沿Z轴方向正四面体传声器的精度明显优于六传声器.

2.2角度误差比较与分析

在平面波作用下，正四面体传声器和六传声器的方向性误差随频率的变化情况如图5所示.

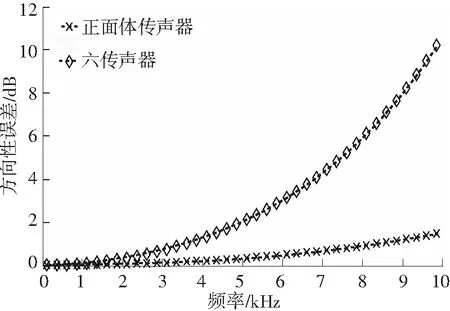
图5　不同传声器的方向性误差随频率的变化

Fig.5The differences in directional bias between different probes as frequency increases

由图5可见，随着频率f增加，两者的方向性误差均有不同程度的升高；六传声器在f=8kHz时，角度偏差已接近6°，精度较低；正四面体传声器高频误差虽有提升，但10kHz时，角度偏差仅为1.8°.由此可见对于平面波作用下的方向性偏差，正四面体传声器相对于六传声器具有较大的优势.

3　全消声室实验验证

3.1实验平面波近似条件

为了进一步确保数值计算的结果符合实际情况，在全消声室中对系统误差进行实验验证，图6为实验现场所拍照片，点声源与传声器阵列几何中心距离大于2m，传声器阵列外接球半径约为15mm.相对于理想状态下的平面波测试，幅值结果相差约0.000 2dB，1kHz时角度相差约1.2°，因此实验可近似认为在平面波作用下进行[14].

图6　全消声室测试现场图

3.2三维声强系统校准

考虑到各传声器之间可能存在相位不匹配的情况，且不同传声器灵敏度不同，导致电压信号输出不一致而产生固有偏差，因此文中采用测量传递函数的方法对三维声强测量系统进行校准.

校准的主要步骤包括测量标定因子、基准和非基准传递函数计算、利用传递函数修正误差3个方面.对于文中所述实验，假定4号传声器为基准传声器，并标定其幅值，测得声强标定因子C4，利用式(11)计算基准传声器与其他传声器之间的传递函数，利用式(12)计算非基准传声器之间的传递函数.

(11)

(12)

式中，Tij表示两个传声器之间的传递函数；ω为角频率；d为两传声器之间的距离.

3.3实验系统与测量结果

实验采用Core Sound公司生产的Tetra-Mic型正四面体传声器阵列探头，具有较高的灵敏度和较宽的频率响应.测量系统主要由信号采集、信号输出、控制3个模块组成，如图7所示.在数值仿真中，设定各参数初始值与传声器阵列的空间尺度和几何分布保持一致[15-17].

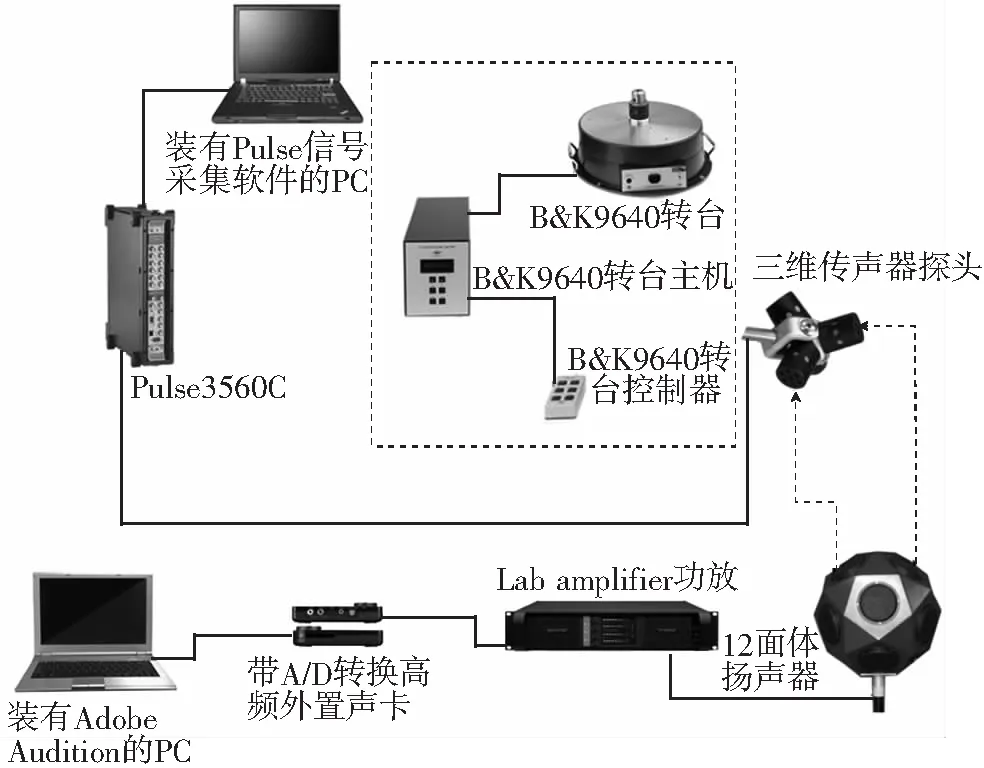
图7　消声室实验系统示意图Fig.7　The system diagram of the experiment in an anechoic chamber

图8　仿真与实测误差比较

Fig.8Comparison of directional bias between predicted and measured data

测试初始位置均采用激光测距仪进行旋转定位，确保声源、4号传声器、几何中心处于同一平面.在全消声室中控制转台以10°为步长顺时针旋转，记录每个测点的相对角度偏差，并计算其平均值.由图8所示实验结果可知，在中频范围内，正四面体传声器角度偏差实测值与仿真值吻合较好，两者最大差值处仅为3°.实验结果进一步表明，在1kHz到3kHz内，数值仿真的结果是合理的.

4　结语

研究平面波作用下三维声强阵列的精度对于噪声源定位、现场法测量隔声、声功率测量等具有重要的现实意义.传声器阵列的空间分布方式和声压振速的估计方法共同决定了几何中心位置的声强测量精度.文中采用数值仿真的方式比较了正四面体传声器和六传声器的幅值和方向性误差，并讨论了平面波入射角沿不同方向入射时，误差随频率的变化情况.研究结果表明：在不考虑室内混响声能和扩散的情况下，两者在可听频域范围内幅值误差均满足测试精度要求；而从方向性误差上看，正四面体传声器明显优于六传声器，尤其是在高频段，两者差值接近6°.相对于六传声器，正四面体传声器降低了成本却提高了测试精度，完全适用于平面声场下的建筑声学测量.

[1]程志伟，叶子文，刘雯.声压法和声强法在车身隔声性能测量中的应用和对比 [J].噪声与振动控制,2012，32(1)：174-177.

CHENG Zhi-wei，YE Zi-wen，Liu Wen，et al.Comparison of sound pressure method and sound intensity method in application to the measurement of sound insulation preformance of vehicle’s body [J].Noise and Vibration Control，2012，32(1)：174-177.

[2]杨文林，彭伟才，张俊杰.非消声水池声强法声功率测试的数值模拟 [J].中国航船研究,2012，7(2)：91-97.

YANG Wen-lin，PENG Wei-cai，ZHANG Jun-jie，et al.Numerical investigation of radiated sound power by sound intensity technology in non-anechoic tank [J].Chinese Journal of Ship Research，2012，7(2)：91-97.

[3]张宸维，李志远，陆益民，等.基于声强技术的叉车变速器噪声源识别研究 [J].工程机械,2011，42(5)：25-29.ZHANG Chen-wei，LI Zhi-yuan，LU Yi-min，et al.Research on noise source identification of forklift transmission based on sound intensity technology [J].Construction Machinery and Equipment，2011，42(5)：25-29.

[4]PASCAL J C，LIB J F.A systematic method to obtain 3D finite-difference formulations for acoustic intensity and other energy quantities [J].Journal of Sound and Vibration，2008，310：1093-1111.

[5]LOCEY L L.Analysis and comparison of three acoustic energy density probes [D].Utah America：Brigham Young University Physics and Astronomy，2004.

[6]SUZUKI H，ANZAI M，OGURO S，et al.Performance evaluation of a three dimensional intensity probe [J].Journal of the Acoustical Society of Japan，1995,16：233-238.

[7]TAKESHI I，HIROKAZU T，HISANOBU M，et al.Numerical evaluation of three-dimensional sound intensity mea-surement accuracies and a proposal for an error correction method [J].Acoustical Science & Technology，2013，34(1)：34-41.

[8]SUZUKI H，OGURO S，ONO T.A sensitivity correction method for a three-dimensional sound intensity probe [J].Acoustical Science & Technology，2000，21(5)：259-265.

[9]CHUNG J Y，POPE J.Practical measurement of acoustic intensity-the two microphone cross spectral method [C]∥Inter-Noise and Noise-Con Congress and Conference Proceedings.San Francisco:[s.n.]，1978：893-900.

[10]WIEDERHOLD C P，GEE K L，BLOTTER Jonathan D，et al.Comparison of multi-microphone probe design and processing methods in measuring acoustic intensity [J].Journal of the Acoustical Society of America，2014，135：2797-2807.

[11]FREDERIC L，JEAN N.A computer simulation of sound power determination using two-microphone sound intensity measurements [J].Journal of the Acoustical Society of America，1992，91：2042-2055.

[12]BROWN H R.DETERMINING A.The direction to a sound source in air using vector sound-intensity probes [J].Journal of the Acoustical Society of America，2011，129：219-224.

[13]JACOBSEN F.An overview of the sources of error in sound power determination using the intensity technique [J].Applied Acoustics，1997(50)：155-166.

[14]MIAH K H，HIXON E L.Design and performance eva-luation of a broadband three dimensional acoustic intensity measuring system [J].Journal of the Acoustical Society of America，2010，127：2338-2346.

[15]MUHLESTEIN M B，THOMAS D C，GEE K L.Time-domain effects of rigid sphere scattering on measurement of transient plane waves [J].Journal of the Acoustical Society of America，2014，136：13-21.

[16]JACOBSEN F.A comparison of two different sound intensity measurement principles [J].Journal of the Acous-tical Society of America，2005，118：1510-1517.

[17]CHUNG J Y.Cross-spectral method of measuring acoustic intensity without error caused by instrument phase mismatch [J].Journal of the Acoustical Society of America，1978，64：1613-1616.

s： Supported by the National Natural Science Foundation of China (51278198)and the Fund of China Scholarship Council(201308440043)

Accuracy Comparison Between Two Sound Intensity Arrays in Plane Wave and the Corresponding Numerical Analysis

WANGHong-wei1,2ZHANGLong1

(1. School of Architecture，South China University of Technology，Guangzhou 510640，Guangdong，China；2. State Key Laboratory of Subtropical Building Science，South China University of Technology，Guangzhou 510640，Guangdong，China)

On the basis of the theoretical derivation of three-dimension sound intensity arrays in plane wave，firstly，the sound pressure and the particle velocity are estimated，and the sound intensity spectrum is calculated. Then，a comparison of amplitude bias and directional bias is made between a tetrahedral microphones system and a six-microphone system. Finally，the numerical simulation results are verified through experiments in an anechoic chamber. It is found that (1) the magnitude bias expands exponentially as frequency increases； (2) the amplitude biases of the two systems are both less than 0.5 dB within the range from 0 Hz to 4 kHz，which means that the systems both meet the accuracy requirements； (3) the tetrahedral microphones system is superior to the six-microphone system； and (4) the directional bias of six-microphone system is close to 6° at a frequency of 8 kHz，while that of tetra-hedral approach is only 1° and increases slowly in the whole frequency domain，which means that the tetrahedral microphones system exhibits higher directional accuracy than the six-microphone system.

plane wave； three-dimension sound intensity； microphone； sound pressure； numerical simulation； amplitude bias； directional bias

1000-565X(2016)07-0090-06

2016-03-16

国家自然科学基金资助项目(51278198)；国家留学基金资助项目(201308440043)；华南理工大学中央高校基本科研业务费专项资金资助项目(2014zz0021)

王红卫(1975-)，男，博士，副教授，主要从事建筑和环境声学研究.E-mail：wanghw@scut.edu.cn

TU 212doi： 10.3969/j.issn.1000-565X.2016.07.014