Multilinear Fractional Integrals and Commutators on Generalized Herz Spaces

Yueshan Wangand Yuexiang He

Department of Mathematics，Jiaozuo University，Jiaozuo，Henan 454003，China



Multilinear Fractional Integrals and Commutators on Generalized Herz Spaces

Yueshan Wang∗and Yuexiang He

Department of Mathematics，Jiaozuo University，Jiaozuo，Henan 454003，China

.Suppose→b=（b1，···，bm）∈（BMO）m，IΠbα，mis the iterated commutator of→b and the m-linear multilinear fractional integral operator Iα，m.The purpose of this paper is to discuss the boundedness propertiesof Iα，mand IΠbα，mon generalizedHerz spaces with general Muckenhoupt weights.

Multilinear fractional integral，generalized Herz space，commutator，Muckenhoupt weight.

AMS Subject Classifications:42B20，42B35

1　Introduction

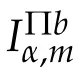
We list some results mentioned above.

Theorem 1.1（see［4］）.Let m≥2 and 0＜α＜mn.Suppose 1/p=1/p1+···+1/pm，1/q=satisfies thecondition，andthen there exists a constant C independent of）such that

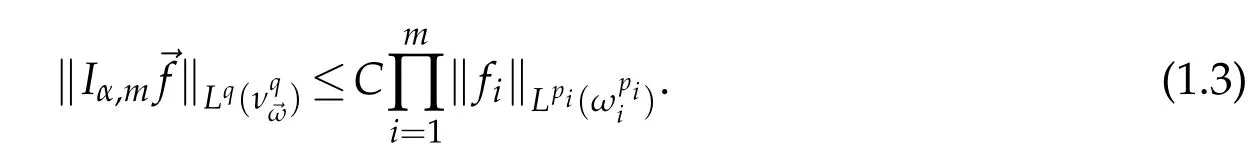
Theorem 1.2（see［5］）.Let 0＜α＜mn andthen there exists a constant C＞0 such that

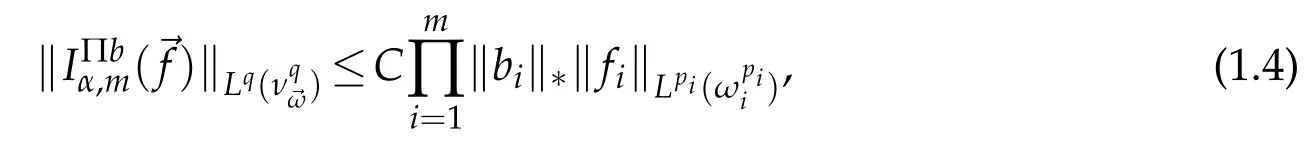
Let Bk=｛x∈Rn:|x|≤2k｝and Ck=BkBk-1for any k∈Z.Denote χk=χCkfor k∈Z，where χCkis the characteristic function of the set Ck.The following weighted Herz space was introduced by Lu and Yang in［10］.

Let σ∈R，0＜p，q＜∞and ω1，ω2be two weight functions on Rn.The homogeneous weighted Herz space˙Kσ，pq（ω1，ω2）is defined by

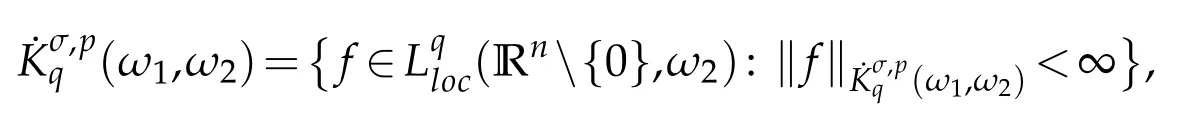
where

In 2000，Lu，Yabuta and Yang in［11］obtained boundedness results for sublinear operators on weighted Herz spaces with general Muckenhoupt weights.Recently，many authors considered the boundedness of operators and their commutators on weighted Herz type spaces.Wang in［12］proved that the intrinsic square functions are bounded on weighted Herz type Hardy spaces.In［13］，Hu and Wang considered parametric Marcinkiewicz integral and its commutator on Weighted Herz spaces.

In［14］，Komori and Matsuoka introduced generalized Herz spaces.

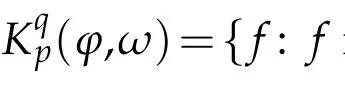
where

Let δ＞0，we say ω∈RD（δ）（centered reverse doubling）if there is a positive numbers C such that

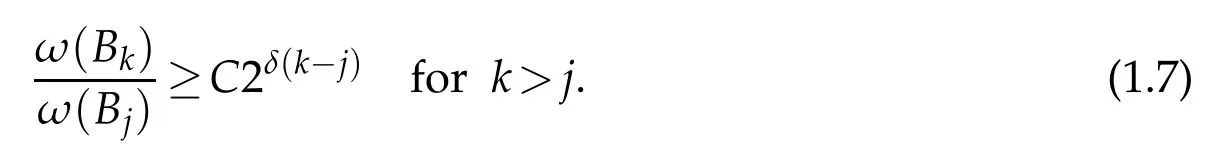
Komori and Matsuoka considered the boundedness of singular integral operators and fractional integral operators on generalized Herz spaces in［14］，and as corollaries of their general theory，they obtained the boundednessof these operators on weighted Herz spaces.Hu，He and Wang in［15］considered the boundedness properties of commutator operators generated by BMO function and fractional function Iαon the generalized Herz spaces.

The aim of the present paper is to investigate the boundedness of multilinear fractional integral operator and its iterated commutator on the generalized Herz spaces.Our results can be formulated as follows.

Theorem 1.3.Let 0＜qi＜∞，0＜αi＜n，let 1＜p1i，p2i＜∞，and let

for i=1，···，m.Set

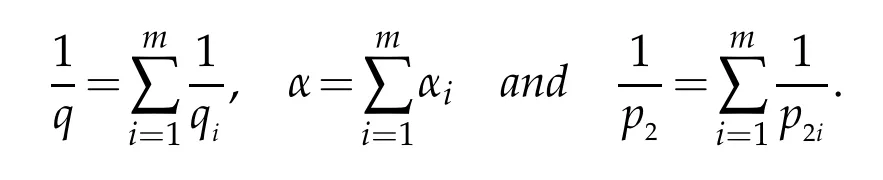
Suppose

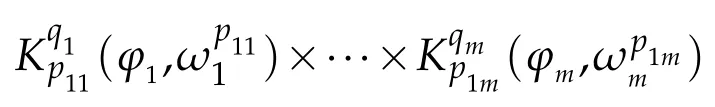
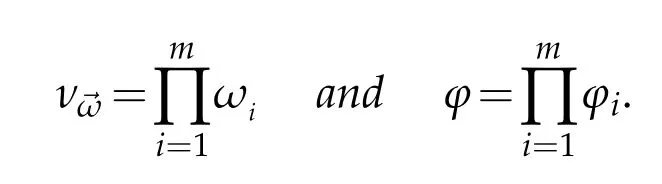
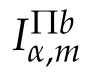
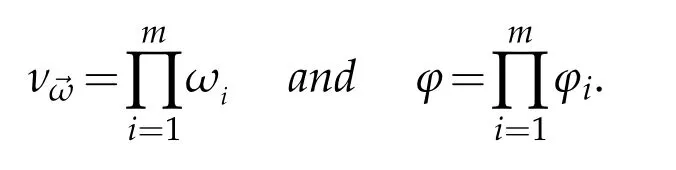
Remark 1.1.In the case m=1，when b1≤0，the condition（2）in Theorem 1.3 is equivalent to the condition that ω∈Ap11，p21，but when b1＞0，（2）is stronger than Ap11，p21-condition. Komori and Matsuoka in［14］showed that the condition（2）is the best possible by a counterexample.

Let ϕi∈D（0，σi）in Theorem 1.3 and Theorem 1.4，we have

Corollary 1.1.Let 0＜qi＜∞，0＜αi＜n，let 0≤σi＜n（1-1/p1i），let 1＜p1i，p2i＜∞，and let

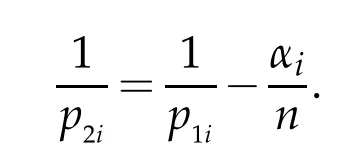
Set

2　Definitions and preliminaries

We begin with some properties of Apweights which play a great role in the proofs of our main results.

A weight ω is a nonnegative，locally integrable function on Rn.Let B=B（x0，rB）denote the ball with the center x0and radius rB.For any λ＞0，let λB=B（x0，λrB）.For a given weight function ω and a measurable set E，we also denote the Lebesgue measure of E by|E|and set weighted measure ω（E）=REω（x）dx.

A weight ω is said to belong to Apfor 1＜p＜∞，if there exists a constant C such that for every ball B⊂Rn，

where s′is the dual of s such that 1/s+1/s′=1.The class A1is defined by replacing the above inequality with

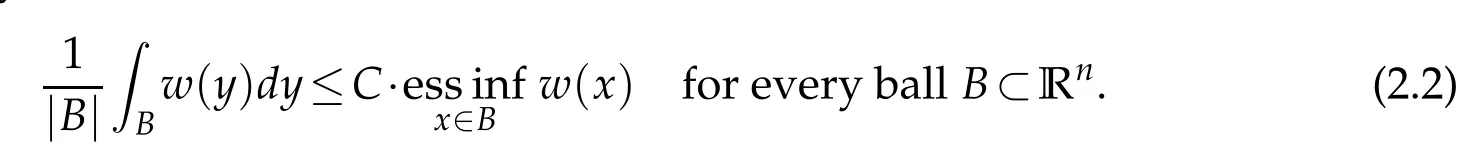
A weight ω is said to belong to A∞if there are positive numbers C and δ so that

for all balls B and all measurable E⊂B.It is well known that

The classical Apweight theory was first introduced by Muckenhoupt in the study of weighted Lp-boundedness of Hardy-Littlewood maximal function in［16］.

Lemma 2.1.Suppose ω∈Apand the following statements hold.

（i）For any 1≤p＜∞，there exists a positive numbers C such that

（ii）For some δ＞0，ω∈RD（δ），that is

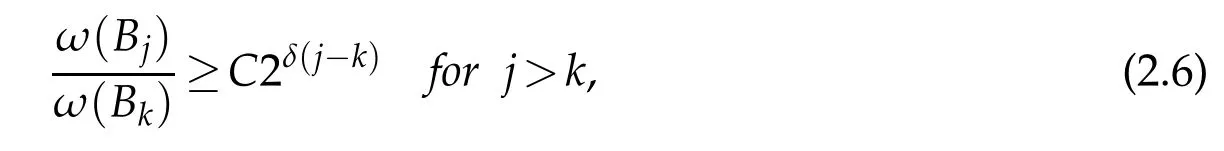
（iii）For any 1＜p＜∞，there is some¯r，1＜¯r＜p such that ω∈A¯r.

We also need another weight class Ap，qintroduced by Muckenhoupt and Wheeden in［17］to studied weighted boundedness of fractional integral operators.

Given 1≤p≤q＜∞.We say that ω∈Ap，qif there exists a constant C such that for every ball B⊂Rn，the inequality

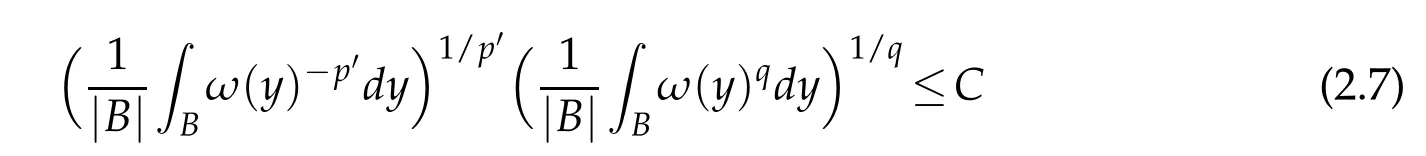
holds when 1＜p＜∞，and the inequality

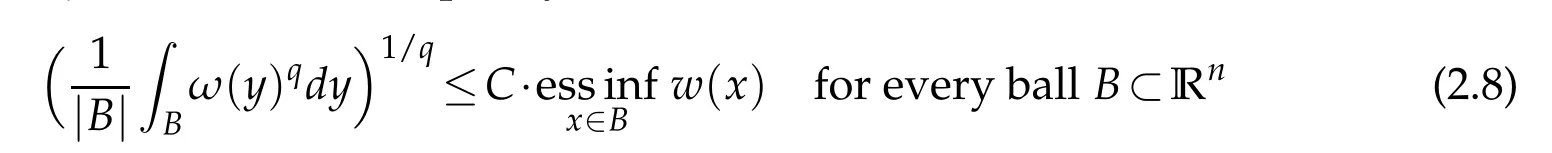
holds when p=1.

By（2.7），we have

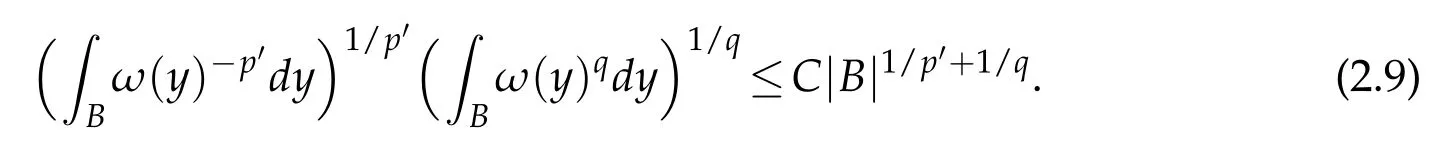
We summarize some properties about weights Ap，q（see［17，18］）.

Lemma 2.2.Given 1≤p≤q＜∞，

（i）ω∈Ap，qif and only if ωq∈A1+q/p′，

（ii）ω∈Ap，qif and only if ω-p′∈A1+p′/q，

（iii）If p1＜p2and q2＞q1，then Ap1，q1⊂Ap2，q2.

Let us recall the definition of multiple weights.For m exponents p1，···，pm，we write，and let q＞0.GivensetWe say that→ω satisfies the A→p，qcondition if it satisfies

By Remark 3.3 in［4］，we have

Lemma 2.3.Let 1/q=1/q1+···+1/pm.If 1≤pi≤qi，ωi∈Api，qifor i=1，···，m，then

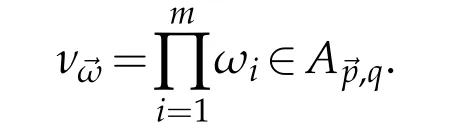
Lemma 2.4（see［4］）.Let 0＜α＜mn，and，and letthen

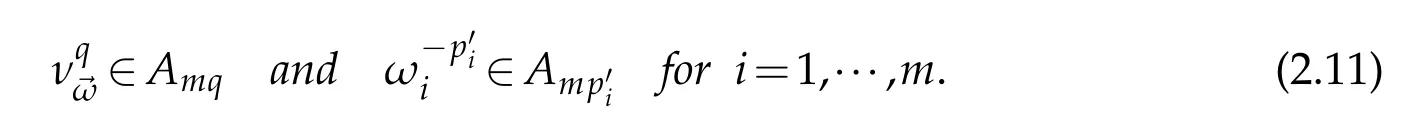
Following［19］，a locally integrable function b is said to be in BMO if

where bB=|B|-1RBb（y）dy.

Lemma 2.5（see［9］）.Suppose ω∈A∞and b∈BMO.Then for any 1≤q＜∞and r1，r2＞0，we have

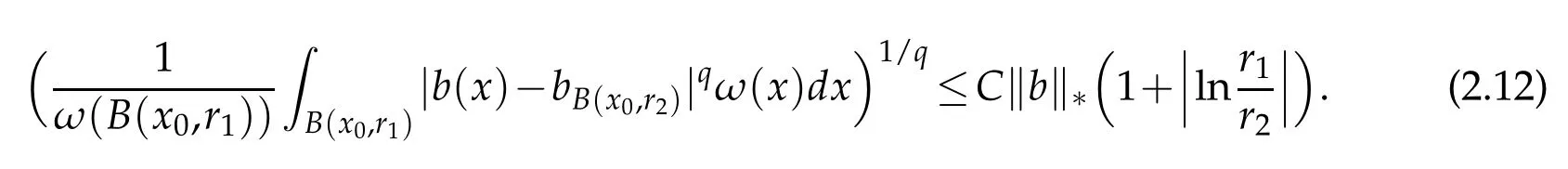
3　Proof of Theorem 1.3

Without loss of generality，we only prove Theorem 1.3 for the case m=2.The method can be extended for any m-linear case without any essential difficulty.

On the other hand，if ϕl∈D（al，bl），l=1，2，we have

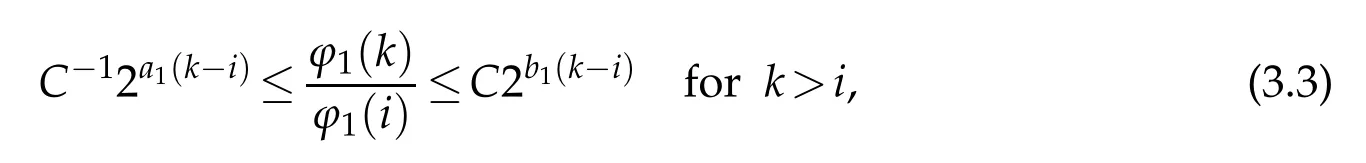
and

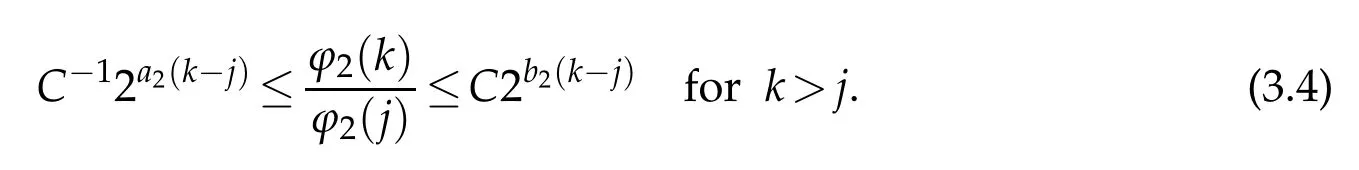
We have the following conclusions.

Theorem 3.1.Let 0＜αl＜n，1＜p1l，p2l＜∞and

for l=1，2.Suppose

We assume that，for l=1，2，

Then

where ν→ω=ω1ω2，and

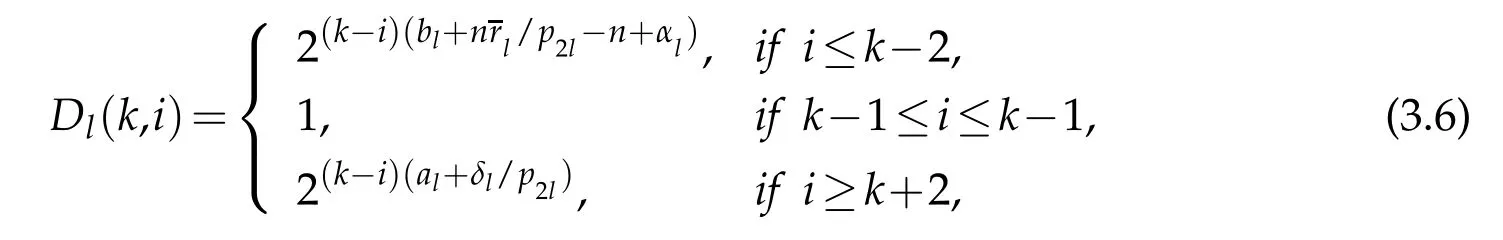
for l=1，2.

This means D1（k，i）=D2（k，j）=1 for k-1≤i，j≤k+1.

In the other case，we see that

for x∈Ck，y1∈Ci，and y2∈Cj.Then

By H¨older's inequality，we get

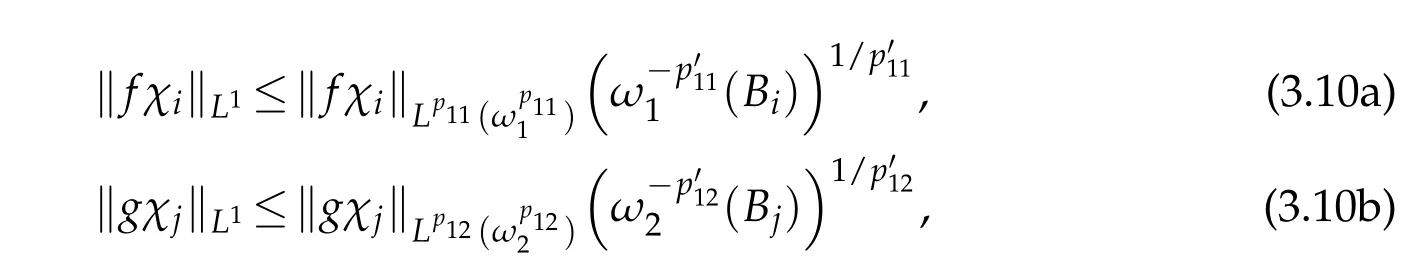
and

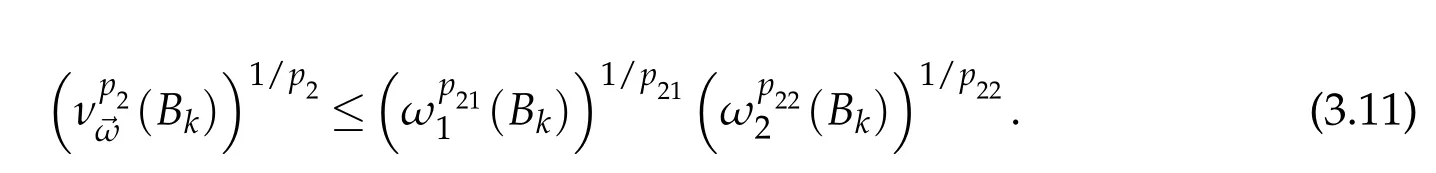
we get

and

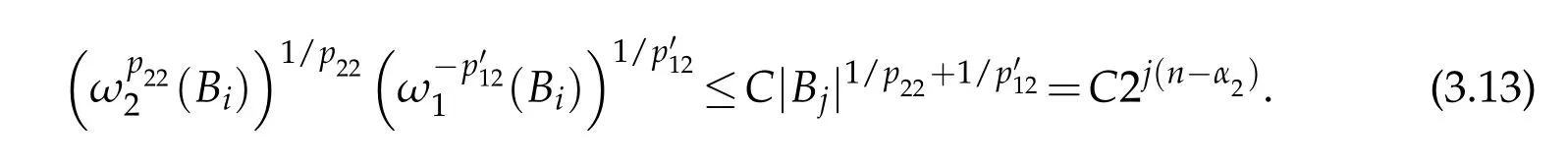
Then，by（3.9）-（3.13），

When i≤k-2，j≤k-2，by（3.1），（3.3），（3.4）and（3.14），we have

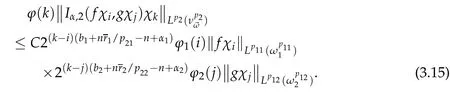
When i≤k-2，j≥k+2，by（3.1）-（3.4），we have

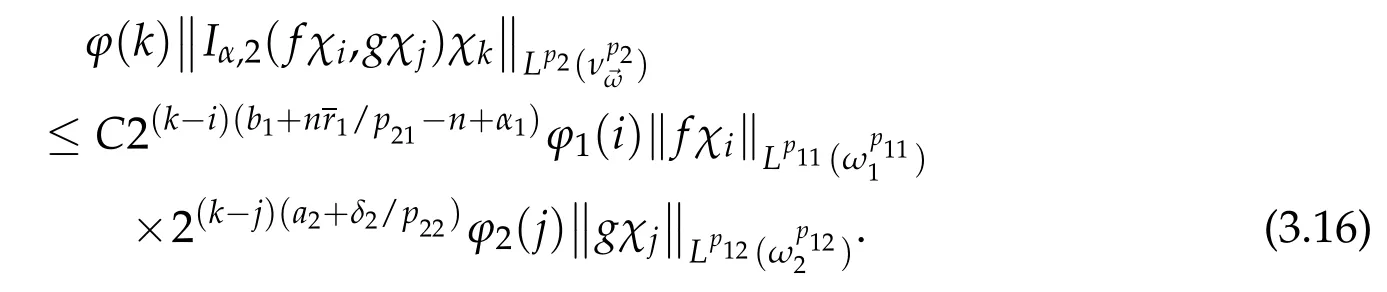
By symmetry，when i≥k+2，j≤k-2，we have

When i≥k+2，j≥k+2，by（3.2）-（3.4），we get

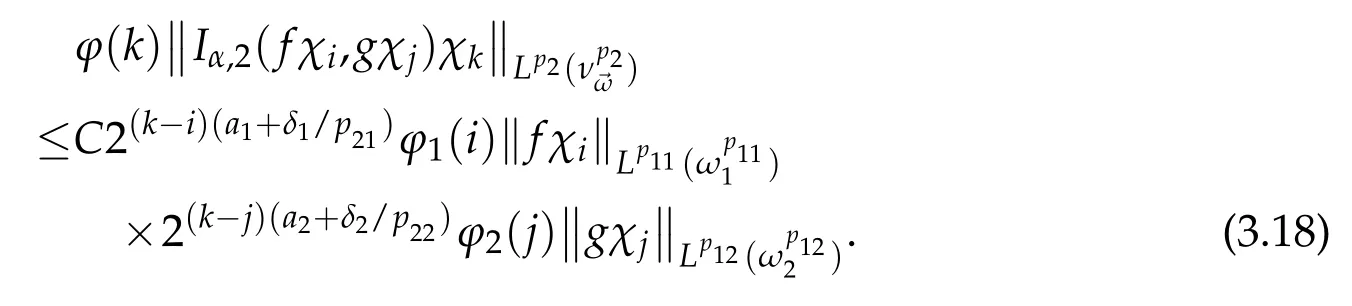
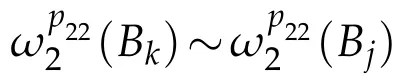
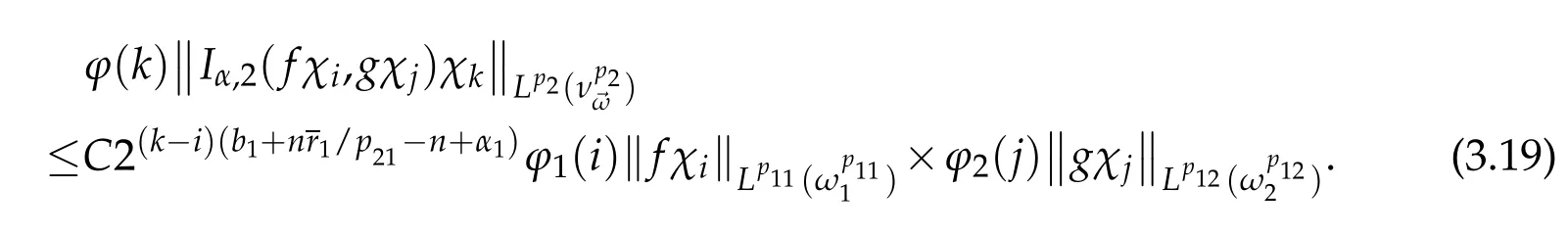
Similar to the estimates（3.19），we can verify（3.5），（3.6）in the following case:k-1≤i≤k+1，j≤k-2，k-1≤i≤k+1，j≥k+2 and i≥k+2，k-1≤j≤k+1.Thus we obtain

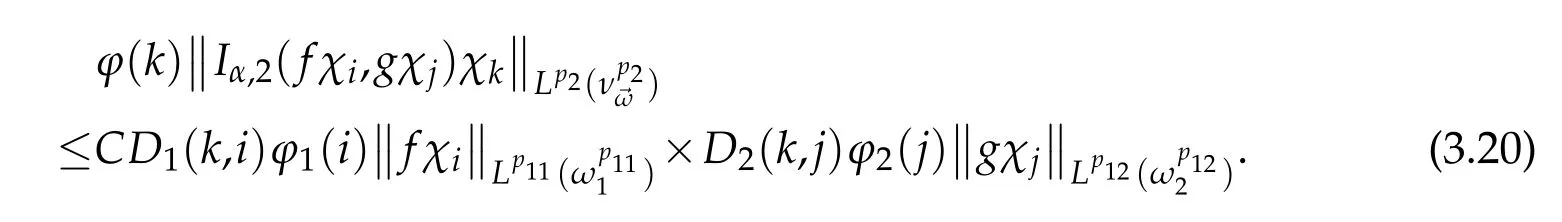
Thus，we complete the proof.

Now，we give the proof of Theorem 1.3. Proof of Theorem 1.3.For l=1，2，since

we get

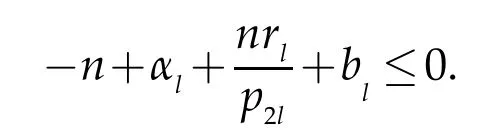
Thus

If p2＞1，by Minkowski's inequality and Theorem 3.1，we have

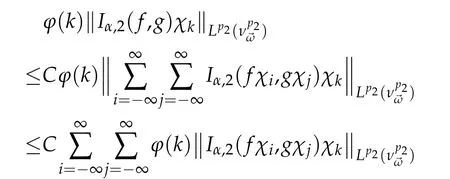
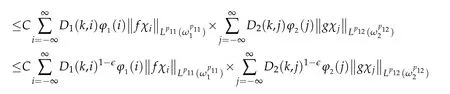
for any 0＜ǫ＜1，since D1（k，i）+D2（k，j）→0 whenever i，j→±∞.

If 0＜p2≤1，note the fact

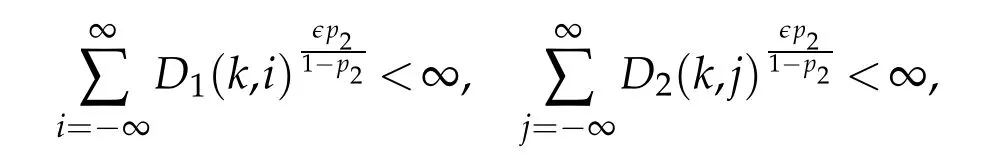
then by Theorem 3.1，the inequality（∑|ai|）p2≤∑|ai|p2，and H¨older's inequality，we have

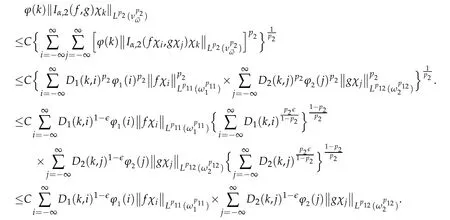
Since 0＜q＜∞，then by H¨older's inequality，=CN1×N2.

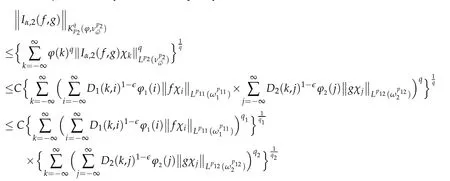
It's enough to show that

By the symmetry，we only give the estimate for N1.

By（3.21）we get

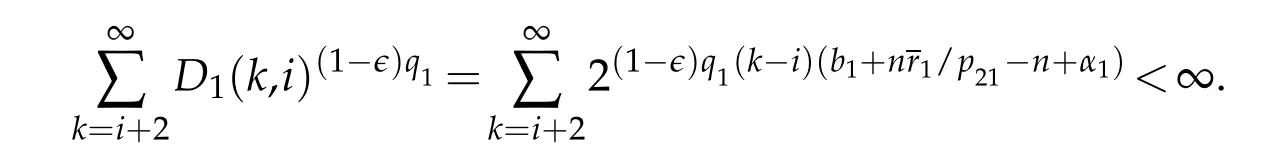
Then，if 0＜q1≤1，from the inequality

we obtain

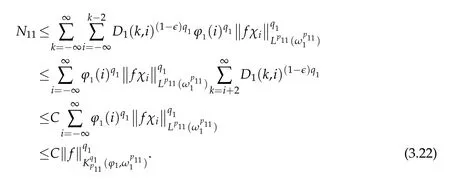
Note that

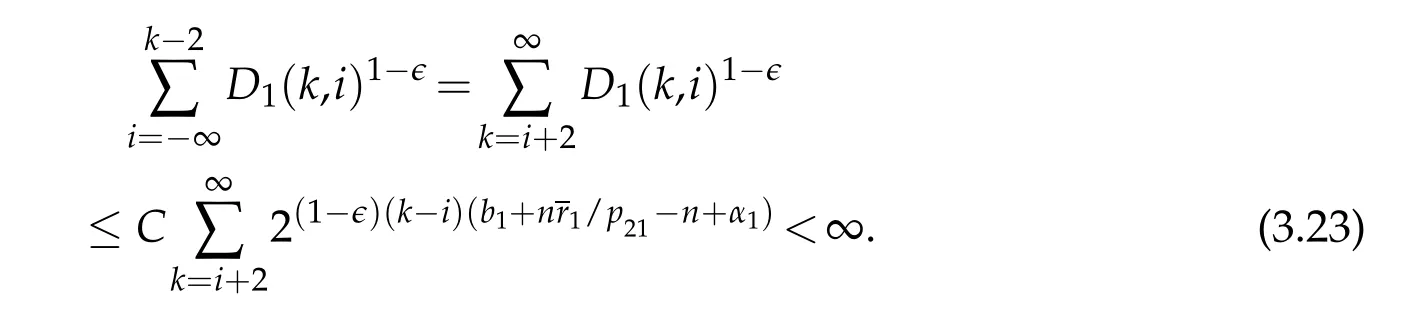
Then for q1＞1，we have

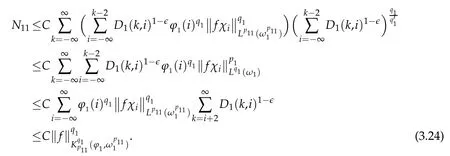
Since D1（k，i）=1 for i=k-1，k，k+1，then

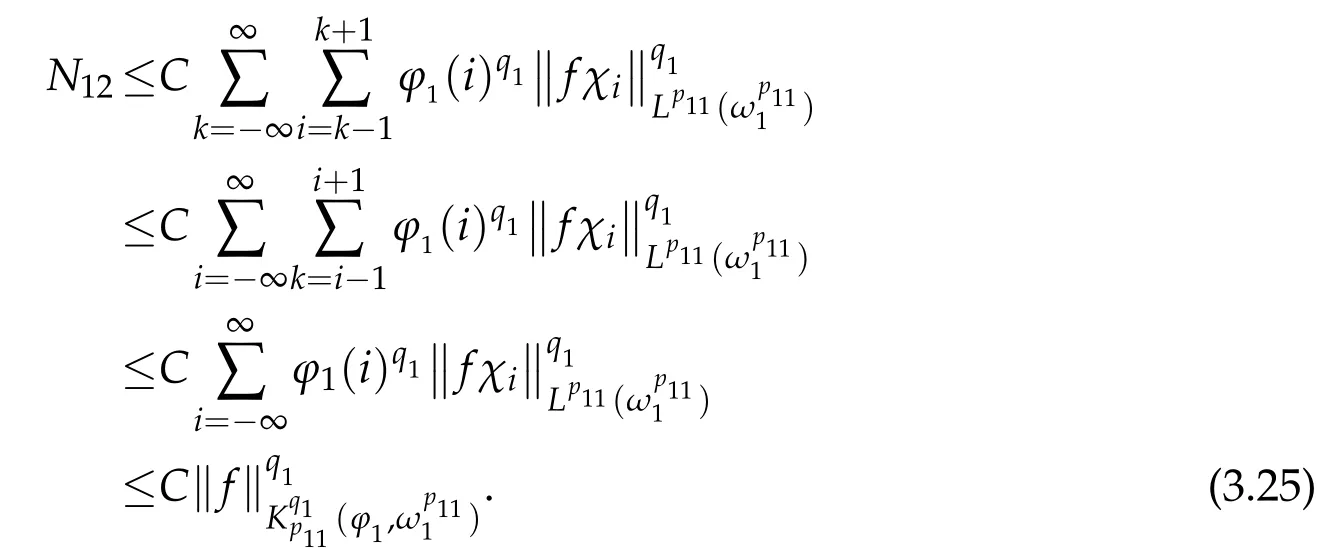
Thus，we have obtained

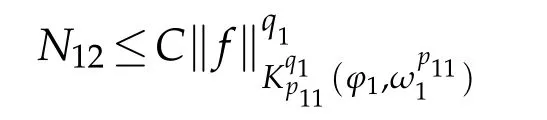
holds for any 0＜q1＜∞.

Let us now turn to estimate the last term N13.If 0＜q1≤1，then

Since a1+δ1/p21＞0，we have

Thus

Note that

Then for q1＞1，we have

This completes the proof of Theorem 1.3.

4　Proof of Theorem 1.4

According to the proof of Theorem 1.3，we just need to prove the following result. Theorem 4.1.Under the hypothesis of Theorem 3.1，if（b1，b2）∈（BMO）2，then

where ν→ω=ω1ω2，and

for l=1，2.

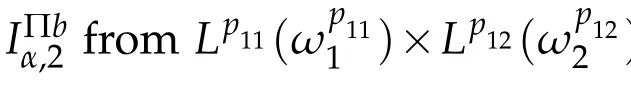
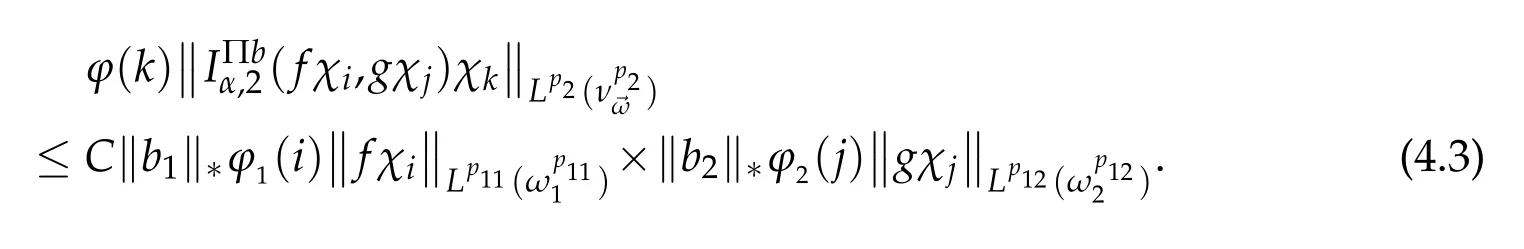
This means E1（k，i）=E2（k，j）=1 if k-1≤i，j≤k+1.

Taking

Then

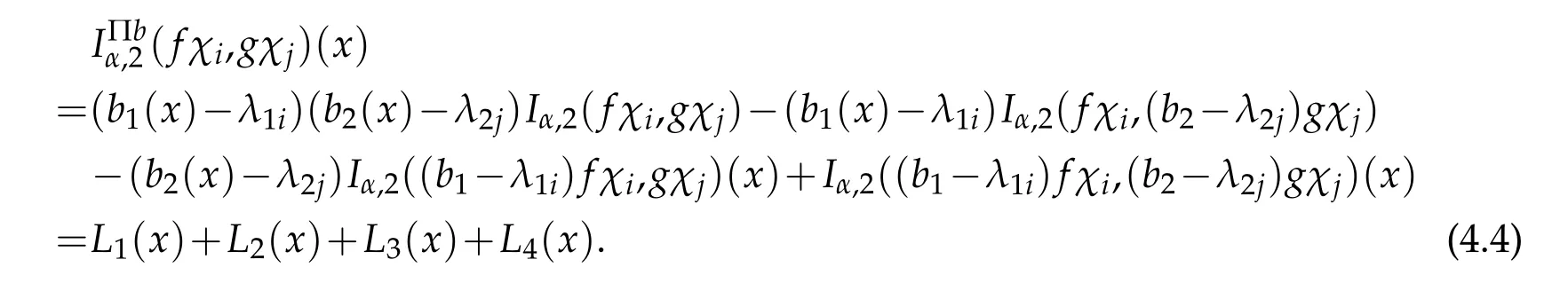
Thus

Now，we will estimate each Jm（m=1，2，3，4），separately.

Applying（3.8）-（3.10b），

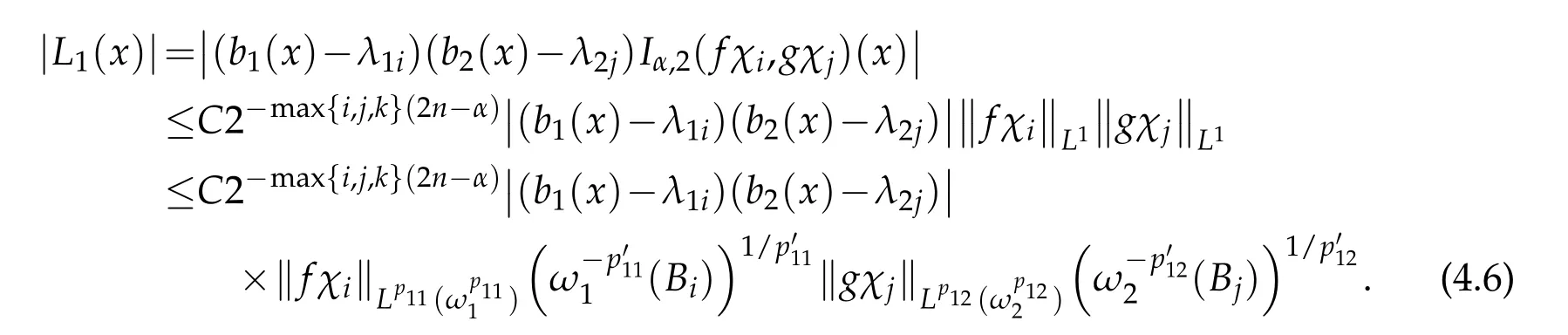
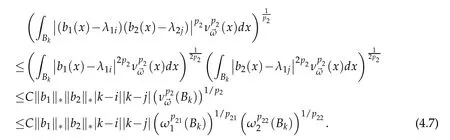
If 0＜p2＜1/2，then by H¨older's inequality and Lemma 2.5 we have

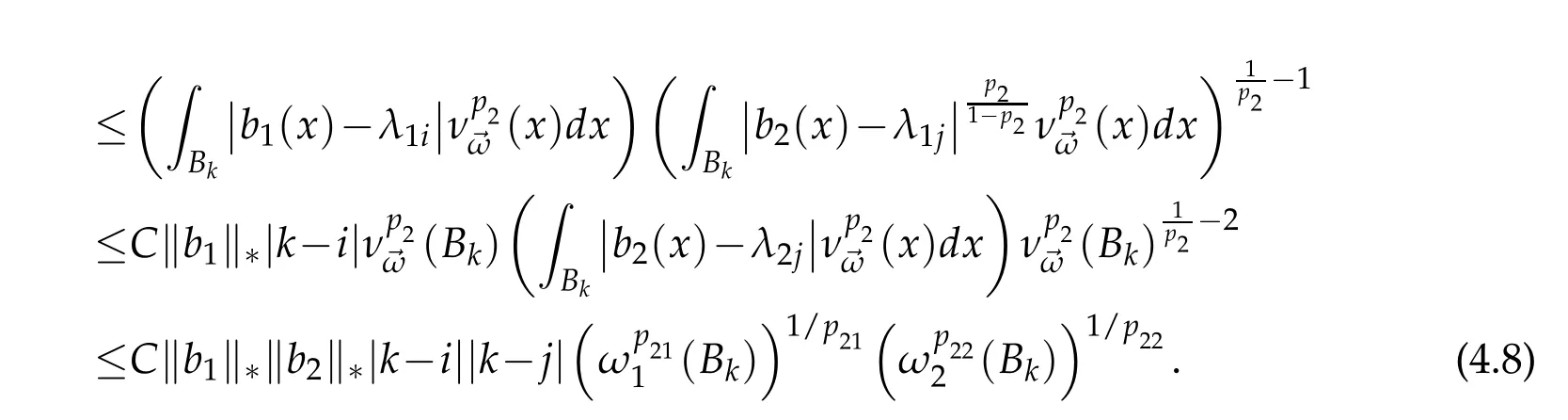
Then by（3.12），（3.13），

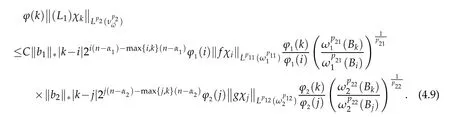
Similar to the estimates in（3.20），we get

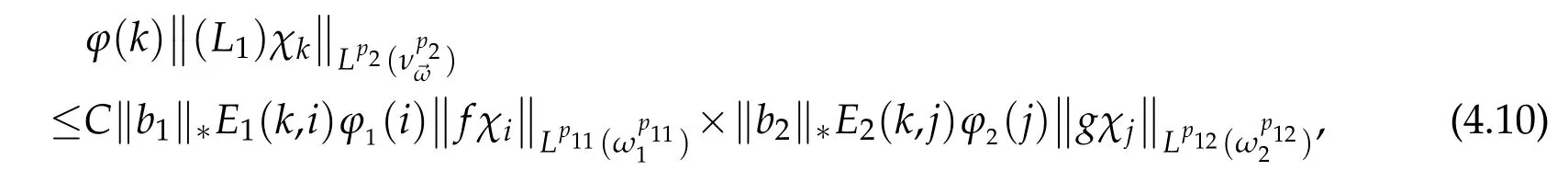
where E1（k，i）and E2（k，j）satisfy（4.2）.

Applying（3.8）and H¨older's inequality，

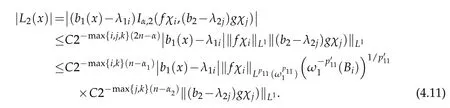
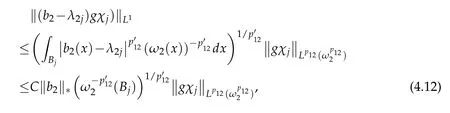
Then by（3.10b）-（3.12）

By symmetry，we also get

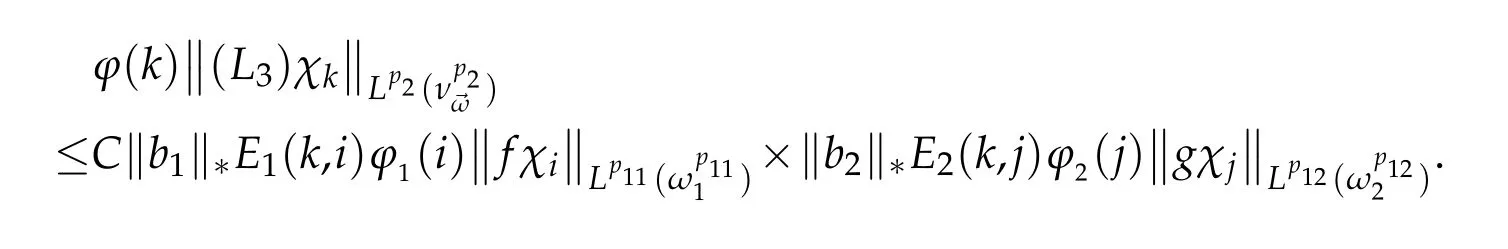
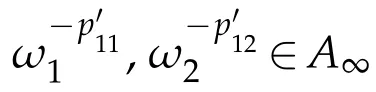
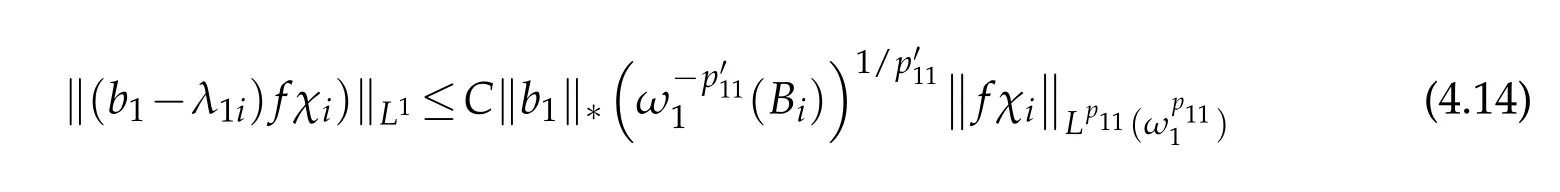
and

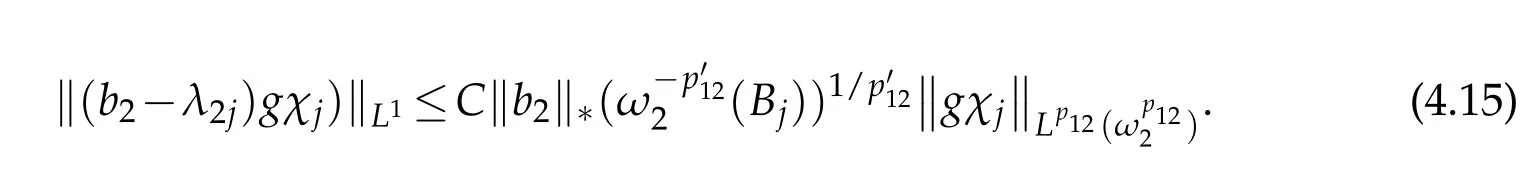
Then

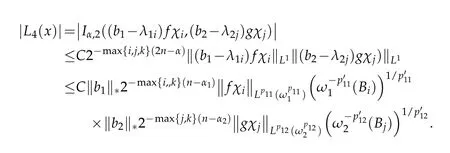
Thus

Then，the proof of Theorem 1.4.is completed

［1］L.Grafakos，On multilinear fractional integrals，Stud.Math.，102（1992），49-56.

［2］C.E.Kenig and E.M.Stein，Multilinearestimates andfractionalintegration，Math.Res.Lett.，6（1996），1-15.

［3］L.Grafakos and N.Kalton，Some remarks on multilinear maps and interpolation，Math. Ann.，319（2001），151-180.

［4］K.Moen，Weighted inequalities for multilinear fractional integral operators，Collect Math.，60（2009），213-238.

［5］S.Chen and H.Wu，Multiple weighted estimates for commutators of multilinear fractional integral operators，Sci.China Math.，56（2013），1879-1894.

［6］X.Chen and Q.Xue，Weighted estimates for a class of multilinear fractional type operators，J.Math.Anal.Appl.，362（2010），355-373.

［7］Z.Si and S.Lu，Weighted estimates for iterated commutators of multilinear fractional operators，Acta Math.Sin.，28（2012），1769-1778.

［8］G.Pradolini，Weighted inequalities and point-wise estimates for the multilinear fractional integral and maximal operators，J.Math.Anal.Appl.，367（2010），640-656.

［9］Y.Hu and Y.Wang，Multilinear fractional integral operators on generalized weighted Morrey spaces，J.Inequal.Appl.，（323）（2014），18 pages.

［10］S.Lu and D.Yang，The decomposition of the weighted Herz spaces on Rnand its applications，Sci.China Ser.A，38（2）（1995），147-158.

［11］S.Lu，K.Yabuta and D.Yang，Boundedness of some sublinear operators in weighted Herztype spaces，Kodai Math.J.，23（3）（2000），391-410.

［12］H.Wang，Some estimates of intrinsic square functions on the weighted Herz-type Hardy spaces，J.Inequal.Appl.，62（2015），22 pages.

［13］Y.Hu and Y.Wang，Parametric Marcinkiewicz integrals on weighted Herz Spaces，Miskolc Math.Notes，16（2）（2015），869-885.

［14］Y.Komori and K.Matsuoka，Boundedness of several operators on weighted Herz spaces，Journal of Function Spaces and Applications，7（1）（2009），1-12.

［15］Y.Hu，Y.He and Y.Wang，The commutators of fractional integrals on generalized Herz spaces，Journal of Function Spaces，2014，Article ID 428493，6 pages.

［16］B.Muckenhoupt，Weighted norm inequalities for the Hardy maximal function，Trans.Amer. Math.Soc.，165（1972），207-226.

［17］B.Muckenhoupt and R.Wheeden，Weighted norm inequalities for fractional integrals，Trans.Amer.Math.Soc.，192（1974），261-274.

［18］J.Garca-Cuervaand J.L.Rubio de Francia，Weighted Norm Inequalities and Related Topics，North-Holland，Amsterdam，1985.

［19］F.John and L.Nirenberg，On functions of bounded mean oscillation，Commun.Pure Appl. Math.，14（1961），415-426.

.Email addresses:wangys1962@163.com（Y.Wang），heyuexiang63@163.com（Y.He）

22 October 2015；Accepted（in revised version）22 January 2016