Commutators ofLittlewood-PaleyOperatorsonHerz Spaces with Variable Exponent

Hongbin Wangand Yihong Wu

1School of Science，Shandong University of Technology，Zibo，Shandong 255049，China

2Department of Recruitment and Employment，Zibo Normal College，Zibo，Shandong 255130，China



Commutators ofLittlewood-PaleyOperatorsonHerz Spaces with Variable Exponent

Hongbin Wang1，∗and Yihong Wu2

1School of Science，Shandong University of Technology，Zibo，Shandong 255049，China

2Department of Recruitment and Employment，Zibo Normal College，Zibo，Shandong 255130，China

.Let Ω∈L2（Sn-1）be homogeneous function of degree zero and b be BMO functions.In this paper，we obtain some boundedness of the Littlewood-Paley Operators and their higher-order commutators on Herz spaces with variable exponent.

Herz space，variable exponent，commutator，area integral，Littlewood-Paley gλ∗function.

AMS Subject Classifications:42B25，42B35，46E30

1　Introduction

The theory of function spaces with variable exponent has extensively studied by researchers since the work of Kov´aˇcik and R´akosn´ık［7］appeared in 1991.In［9］and［10］，the authors proved the boundedness of some Littlewood-Paley operators on variable Lpspaces，respectively.

Given anopenset E⊂Rn，and ameasurable function p（·）:E-→［1，∞），Lp（·）（E）denotes the set of measurable functions f on E such that for some λ＞0，

This set becomes a Banach function space when equipped with the Luxemburg-Nakano norm

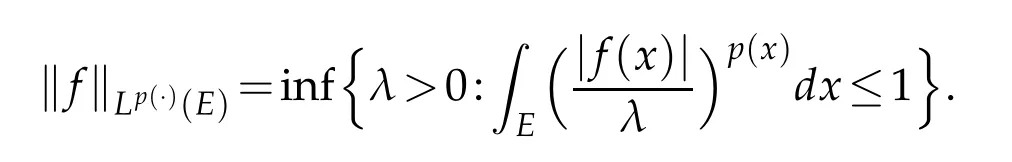
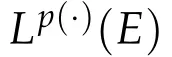
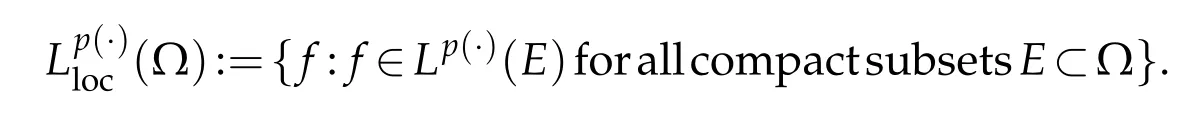
Define P0（E）to be set of p（·）:E-→（0，∞）such that

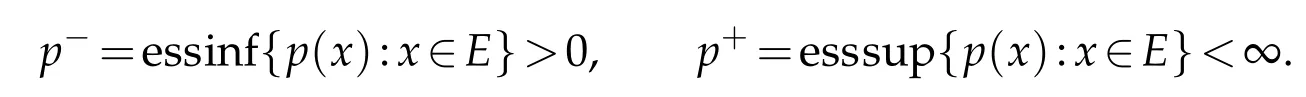
Define P（E）to be set of p（·）:E-→［1，∞）such that

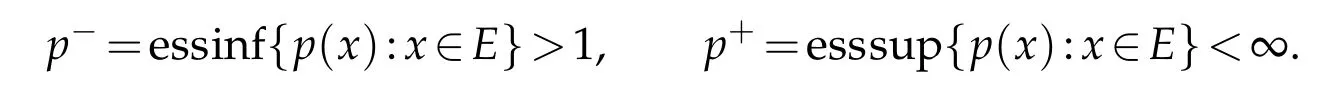
Denote p′（x）=p（x）/（p（x）-1）.

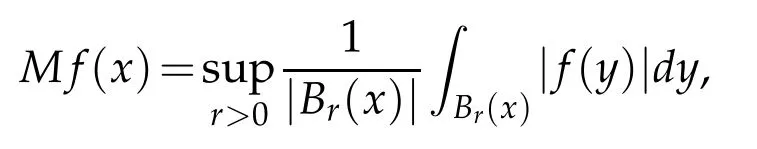
where Br（x）=｛y∈Rn:|x-y|＜r｝.Let B（Rn）be the set of p（·）∈P（Rn）such that the Hardy-Littlewood maximal operator M is bounded on Lp（·）（Rn）.In addition，we denote the Lebesgue measure and the characteristic function of a measurable set A⊂Rnby|A| and χArespectively.The notation f≈g means that there exist constants C1，C2＞0 such that C1g≤f≤C2g.

In variable Lpspaces there are some important lemmas as follows.

Lemma 1.1.If p（·）∈P（Rn）and satisfies

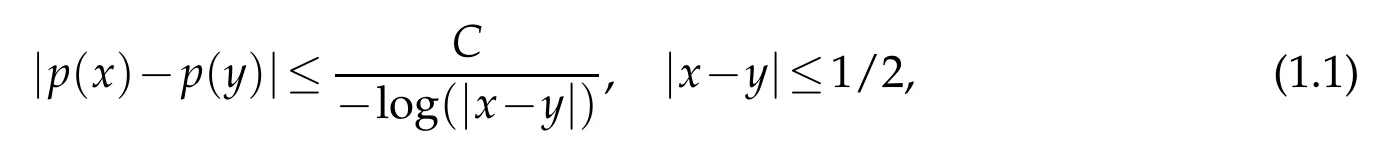
and

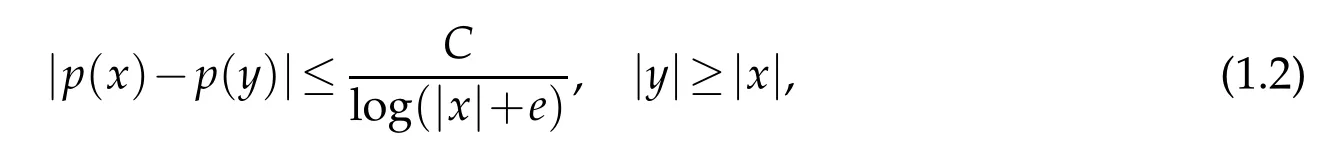
then p（·）∈B（Rn），that is the Hardy-Littlewood maximal operator M is bounded on Lp（·）（Rn）.

Lemma 1.2（see［7］）.Let p（·）∈P（Rn）.If f∈Lp（·）（Rn）and g∈Lp′（·）（Rn），then fg is integrable on Rnand

where

This inequality is named the generalized H¨older inequality with respect to the variable Lpspaces.

Lemma 1.3（see［5］）.Let q（·）∈B（Rn）.Then there exists a positive constant C such that for all balls B in Rnand all measurable subsets S⊂B，

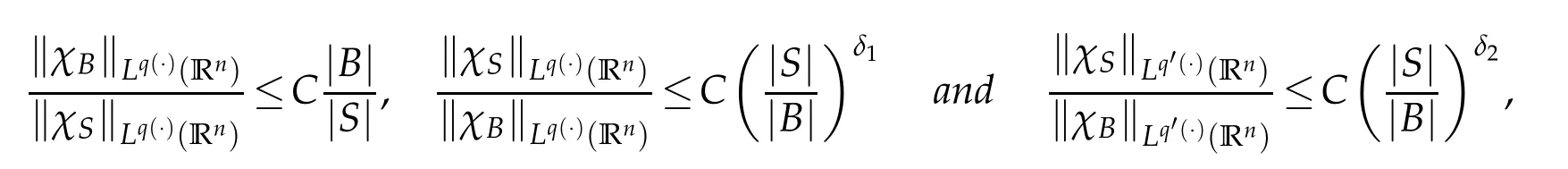
where δ1，δ2are constants with 0＜δ1，δ2＜1.

Throughout this paper δ1，δ2is the same as in Lemma 1.3.

Lemma 1.4（see［5］）.Suppose q（·）∈B（Rn）.Then there exists a constant C＞0 such that for all balls B in Rn，

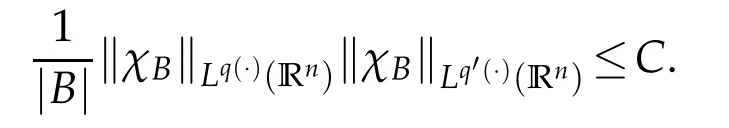
Next we recall the definition of the Herz-type spaces with variable exponent.Let Bk=｛x∈Rn:|x|≤2k｝and Ak=BkBk-1for k∈Z.Denote Z+and N as the sets of all positive and non-negative integers，χk=χAkfor k∈Z，˜χk=χkif k∈Z+and˜χ0=χB0.

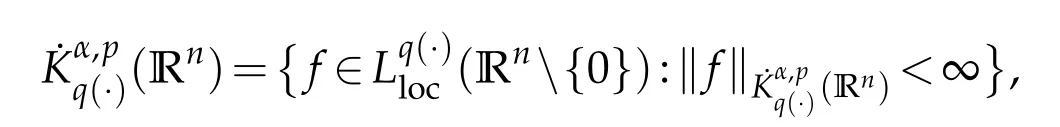
where

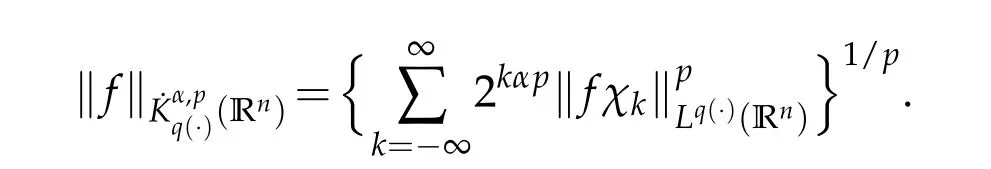
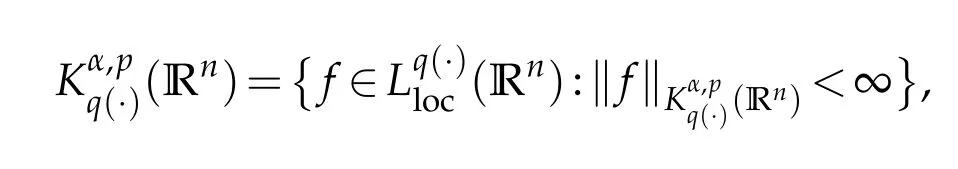
where

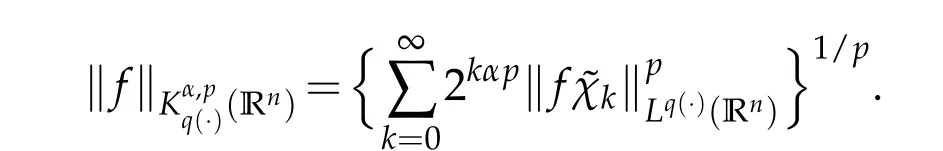
Supposethat Sn-1is the unit sphereof Rn（n≥2）equipped with normalized Lebesgue measure.Let Ω∈L1（Rn），be homogeneous function of degree zero and

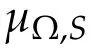
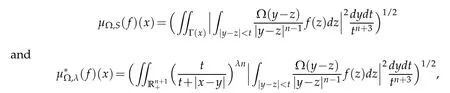
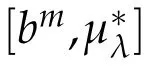
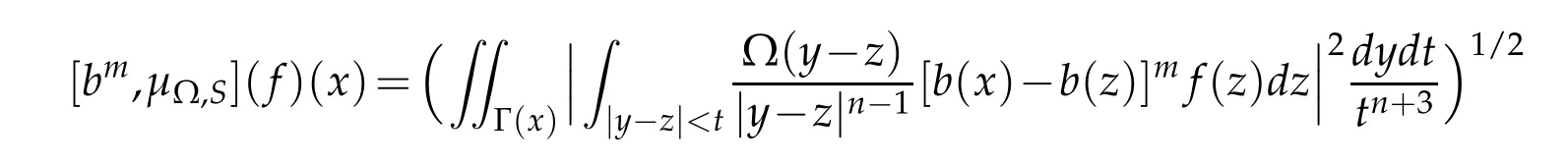
and

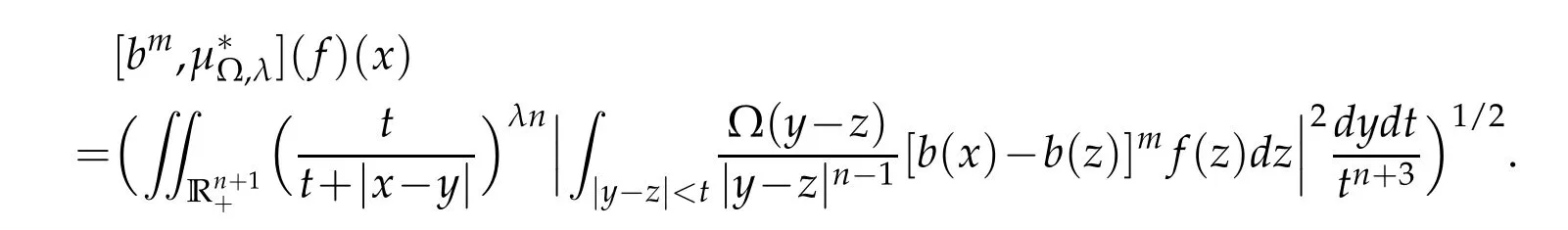
Motivated by［8，9］，we will study the boundedness for the Littlewood-Paley operators and their commutators on the Herz space with variable exponent，where Ω∈L2（Sn-1）.

2　Estimate for the Littlewood-Paley operators

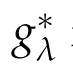
A nonnegative locally integrable function ω on Rnis said to belong to Ap（1＜p＜∞），if there is a constant C＞0 such that

where p′=p/（p-1），Q denotes a cube in Rnwith its sides parallel to the coordinate axes and|Q|denotes the Lebesgue measure of Q.

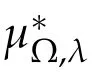
Lemma2.1（see［3］）.Suppose that Ω∈Ls（Sn-1）（s＞1）satisfying（1.3）.Ifω∈Ap/β，max｛s′，2｝= β＜p＜∞，then there is a constant C，independent of f，such that

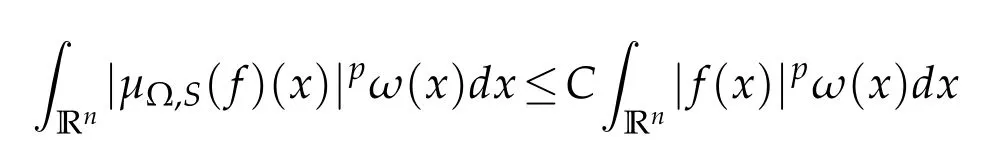
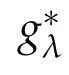
Now we give the main theorem in this section.

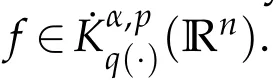
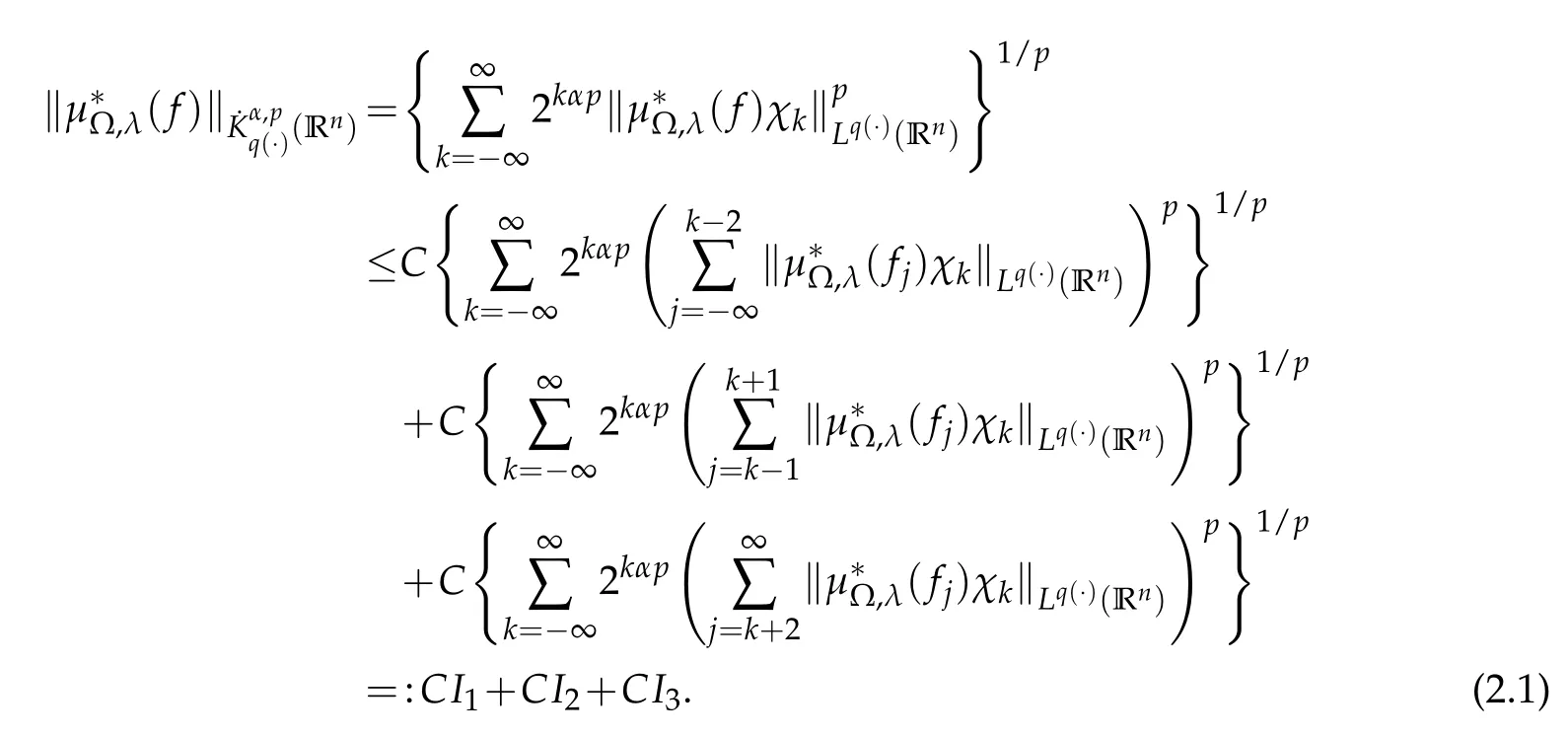
we have

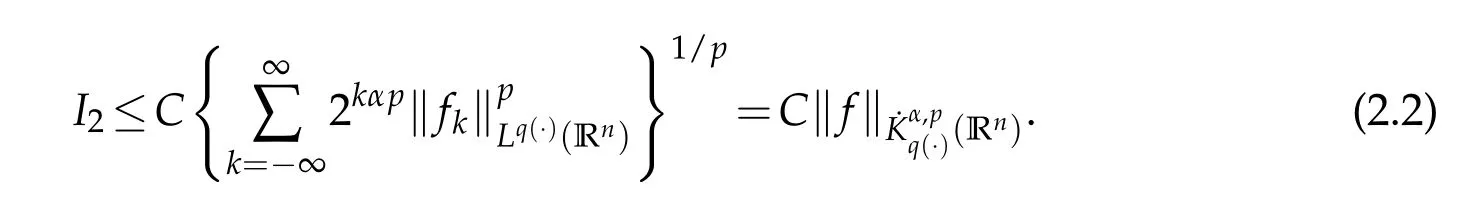
Now we estimate I1.By the Minkowski inequality we have

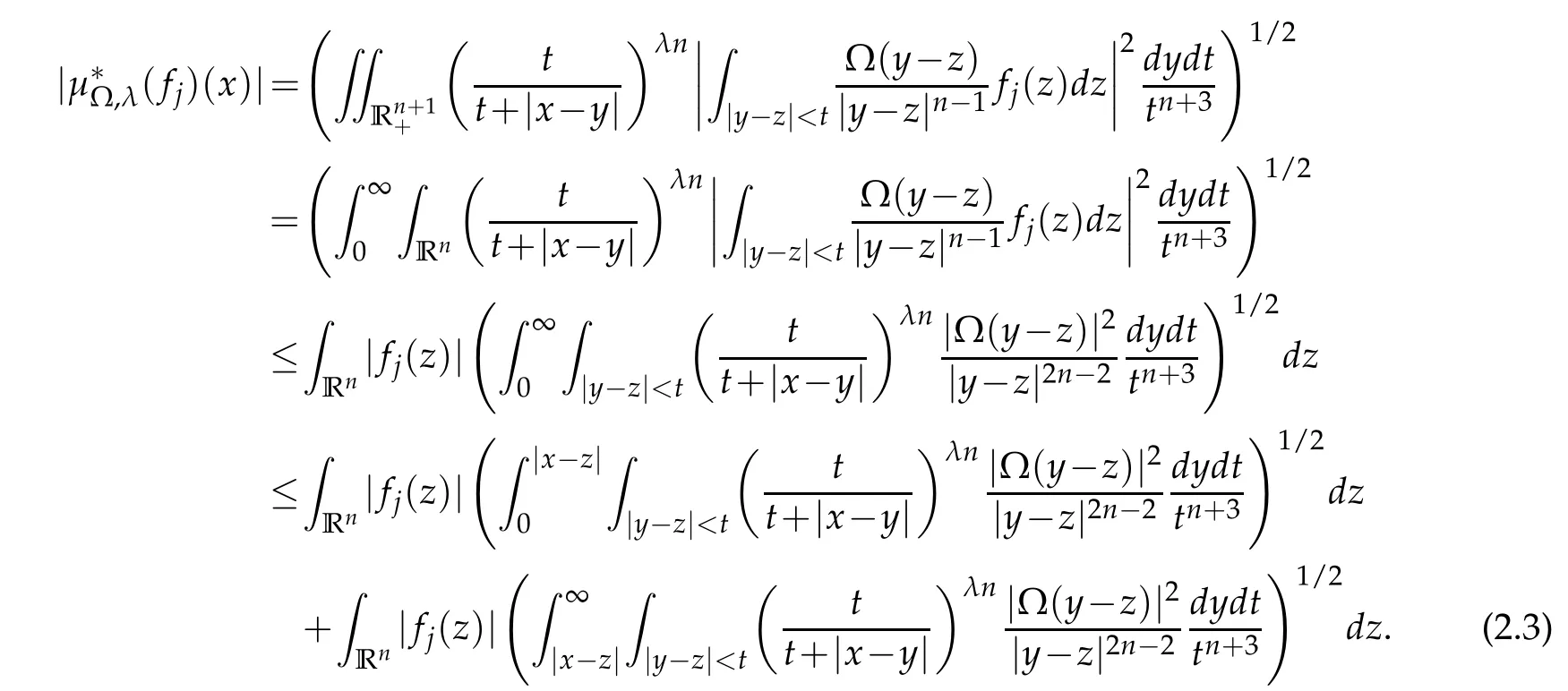
Note that z∈Ajand|y-z|＜t.So we know that|y-z|～|y|，then for Ω∈L2（Sn-1）we have

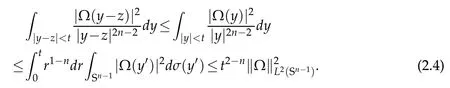
For λ＞2，we take 0＜θ＜（λ-2）n.Since|x-z|≤|x-y|+|y-z|≤|x-y|+t，by（2.4）we have

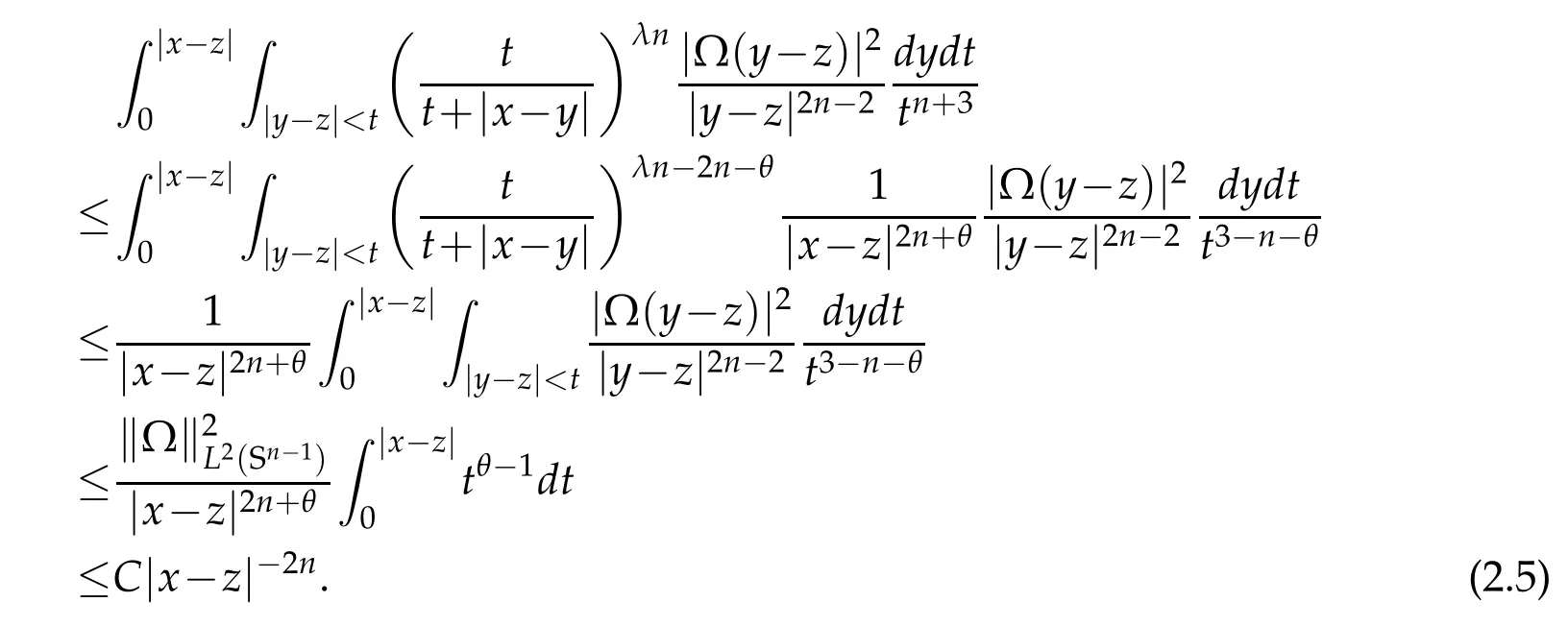
Similarly，noting that|y-z|～|y|，by（2.4）we have

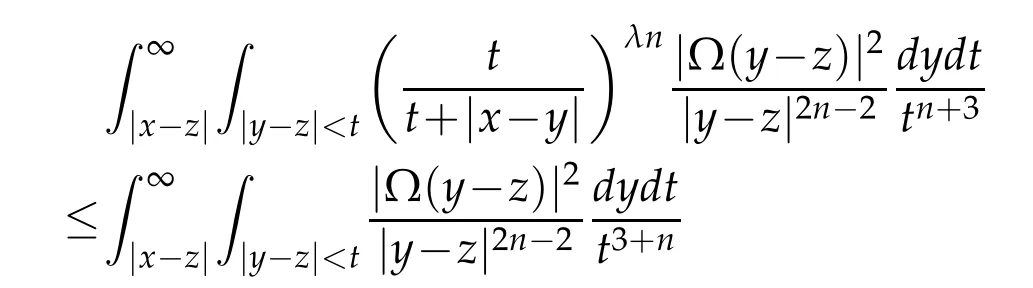
Note that x∈Ak，z∈Ajand j≤k-2.By（2.5），（2.6）and the generalized H¨older inequality we have

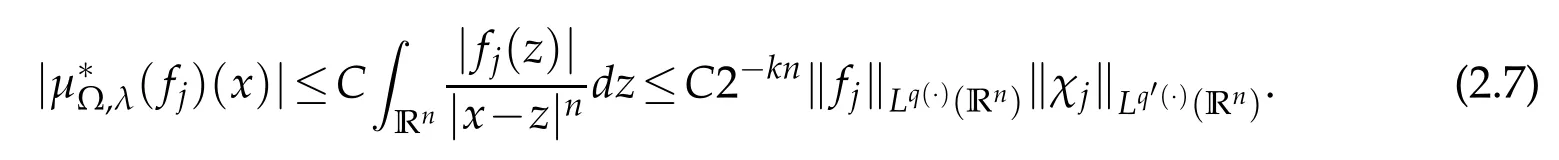
By Lemma 1.3 and Lemma 1.4，we have

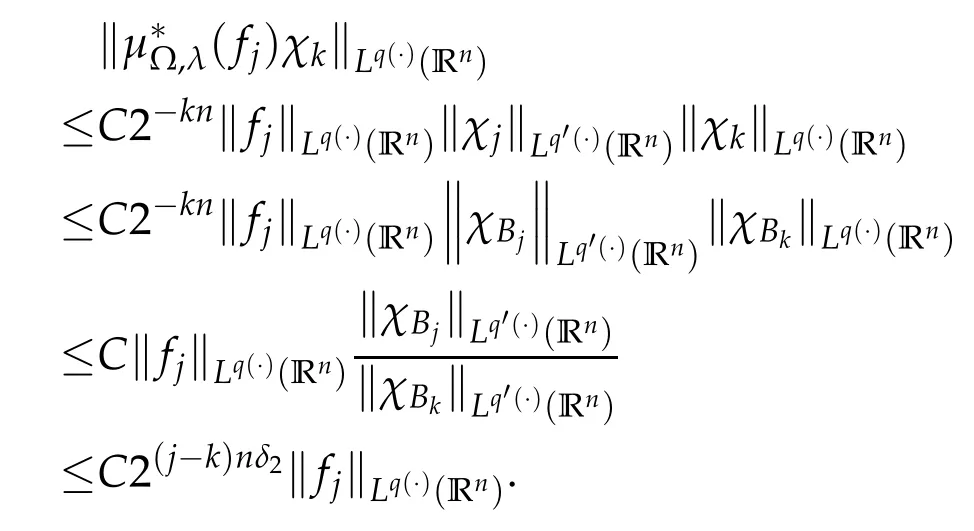
Thus we obtain

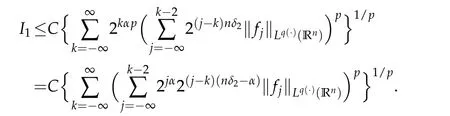
If 1＜p＜∞，take 1/p+1/p′=1.Since nδ2-α＞0，by the H¨older inequality we have

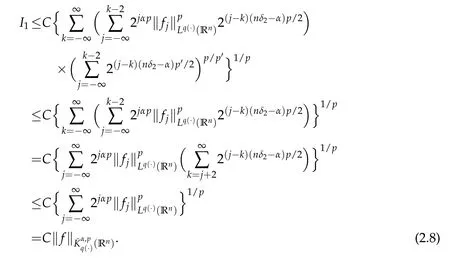
If 0＜p≤1，then we have

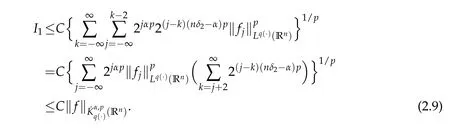
Let us now estimate I3.Note that x∈Ak，y∈Ajand j≥k+2，so we have|y-z|～|y|. By（2.3）-（2.6）and the generalized H¨older inequality we have

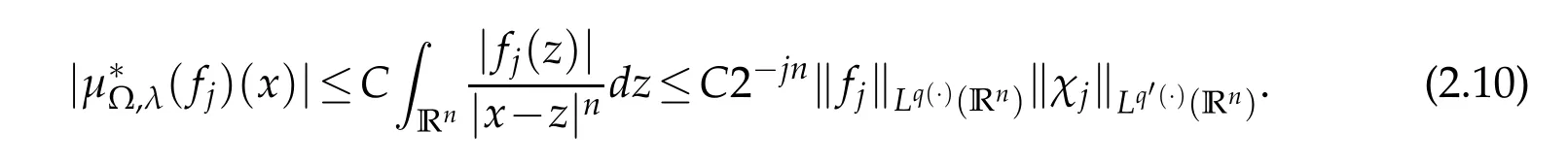
By Lemma 1.3 and Lemma 1.4，we have

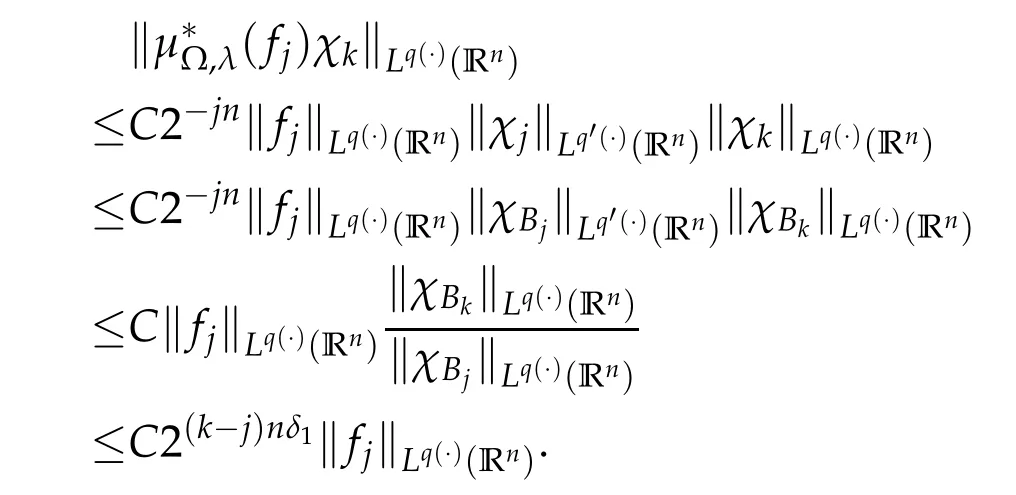
Thus we obtain

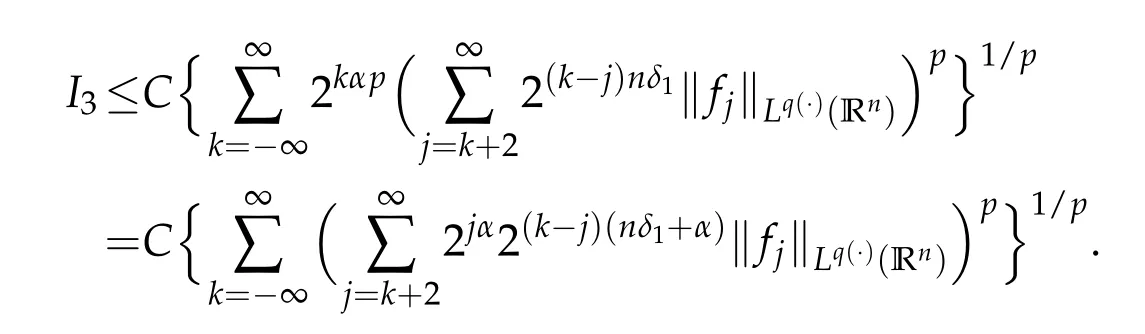
If 1＜p＜∞，take 1/p+1/p′=1.Since nδ1+α＞0，by the H¨older inequality we have

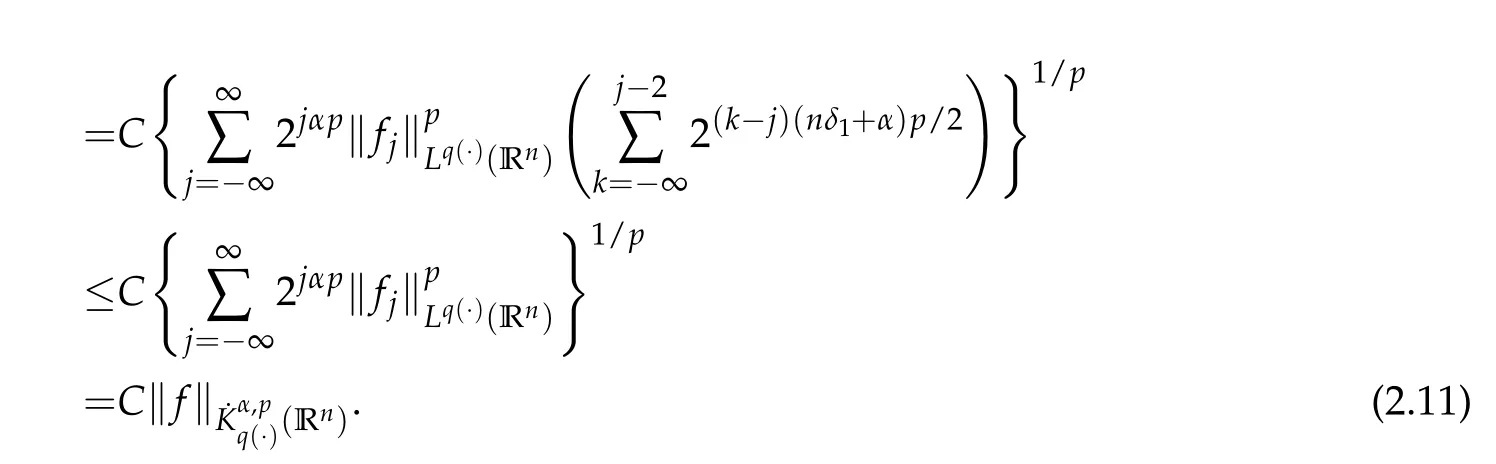
If 0＜p≤1，then we have

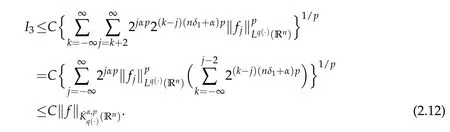
Therefore，by（2.1），（2.2），（2.8），（2.9），（2.11）and（2.12），we complete the proof of Theorem 2.1.

3　BMO estimate for the commutators of Littlewood-Paley operators

Let us first recall that the space BMO（Rn）consists of all locally integrable functions f such that

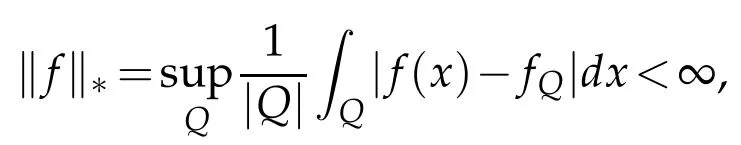
where fQ=|Q|-1RQf（y）dy，the supremum is taken over all cubes Q⊂Rnwith sides parallel to the coordinate axes and|Q|denotes the Lebesgue measure of Q.

Let b∈BMO（Rn）.The weighted（Lp，Lp）boundedness of［b，µΩ］have been proved by Ding，Lu and Yabuta［4］.

Lemma 3.1（see［4］）.Suppose that Ω∈Ls（Sn-1）（s＞1）satisfying（1.3）.For an integer m≥1，if b∈BMO（Rn）and ω∈Ap/β，max｛s′，2｝=β＜p＜∞，then there is a constant C，independent of f，such thatZ

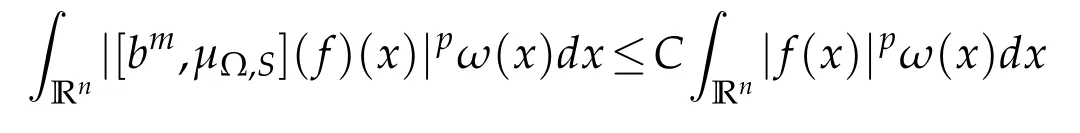
and

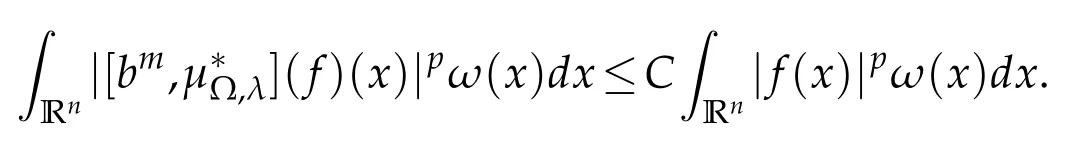
By Lemma 3.1 and Lemma 2.2，it is easy to get the（Lp（·）（Rn），Lp（·）（Rn））-boundedness of the commutators［bm，µΩ，S］and［bm，µ∗Ω，λ］.

Next，we will give the corresponding result about the commutator［b，µΩ］on Herztype Hardy spaces with variable exponent.

In the proof of Theorem 3.1，we also need the following lemma.

Lemma 3.2（see［6］）.Let p（·）∈B（Rn），m be a positive integer and B be a ball in Rn.Then we have that for all b∈BMO（Rn）and all j，i∈Z with j＞i，

where Bi=｛x∈Rn:|x|≤2i｝and Bj=｛x∈Rn:|x|≤2j｝.

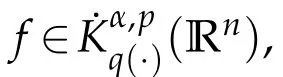
Then we have

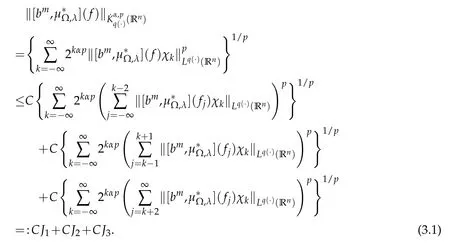
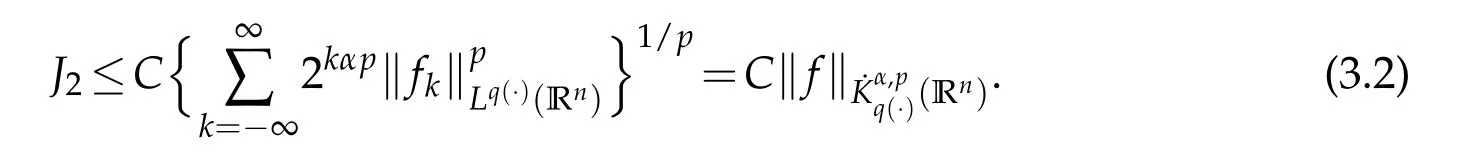
Now we estimate J1.By the Minkowski inequality we have

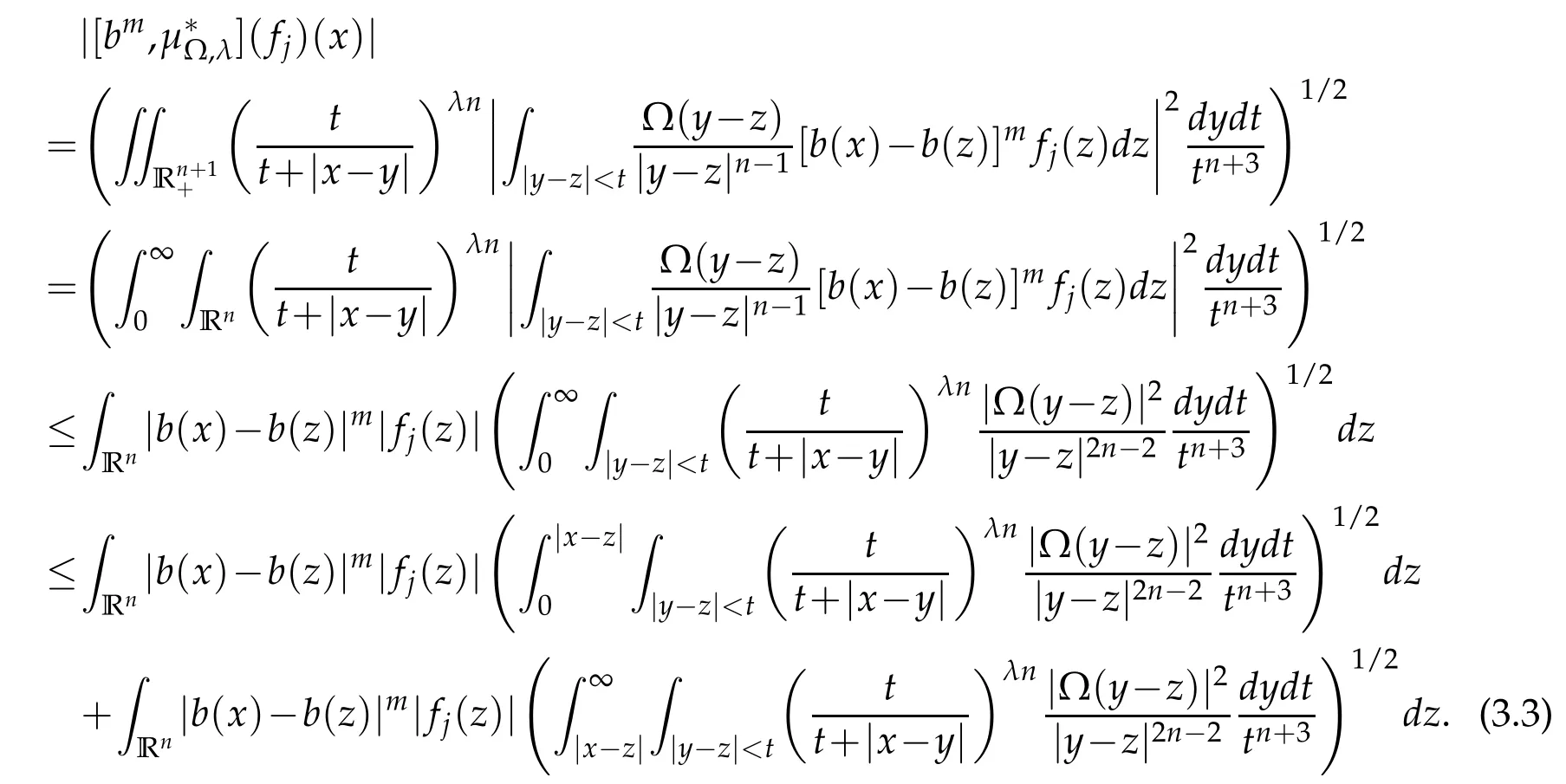
Note that x∈Ak，z∈Ajand j≤k-2.By（2.5），（2.6）and the generalized H¨older inequality we have

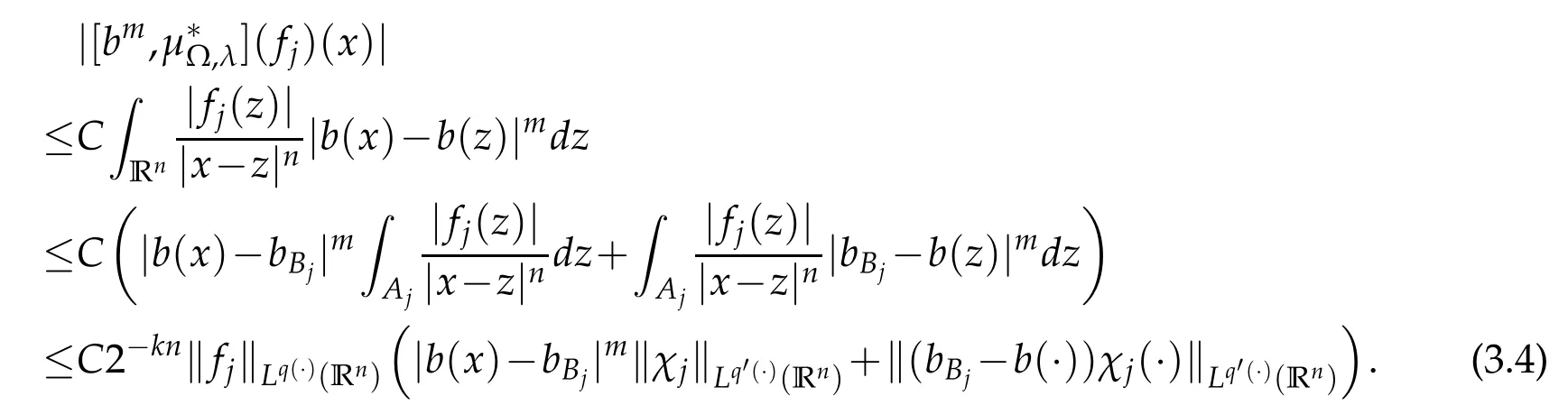
By Lemma 1.3，Lemma 1.4 and Lemma 3.2 we have

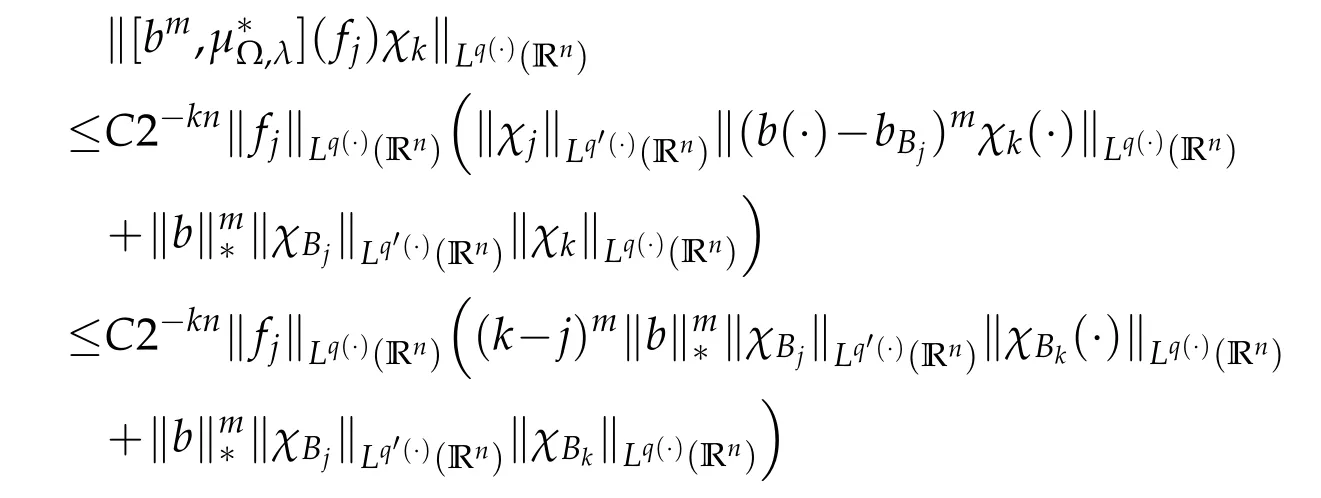
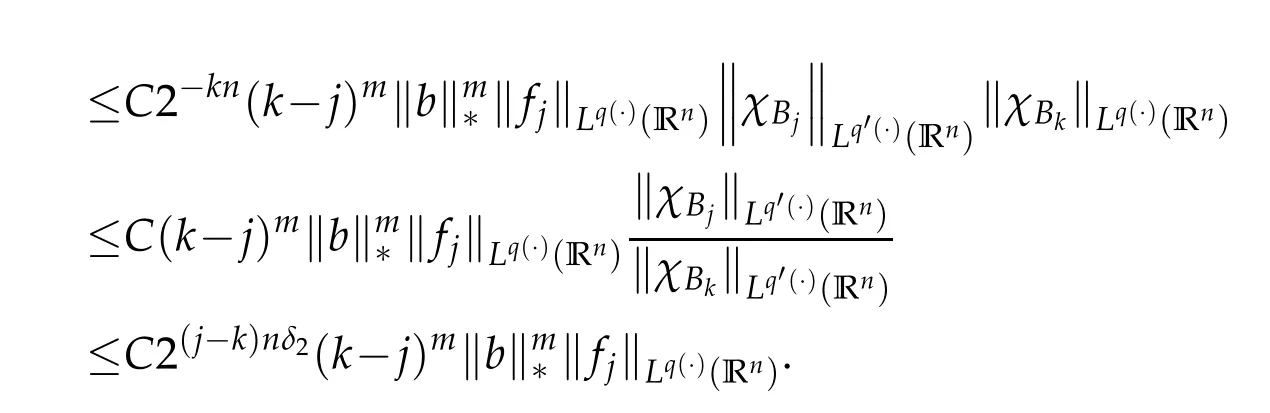
Thus we obtain

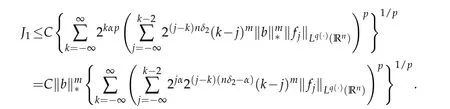
If 1＜p＜∞，take 1/p+1/p′=1.Since nδ2-α＞0，by the H¨older inequality we have

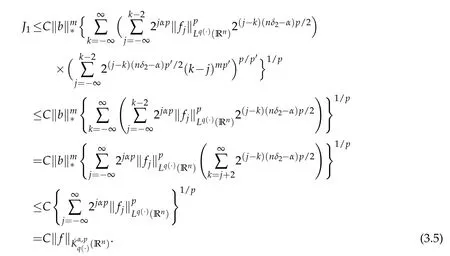
If 0＜p≤1，then we have

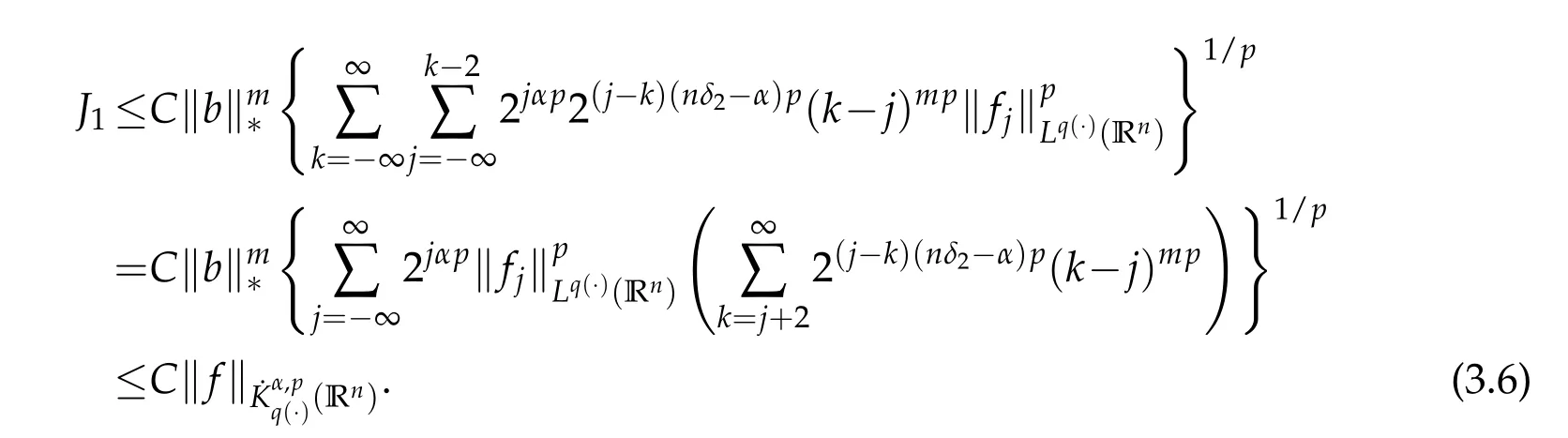
Let us now estimate J3.Note that x∈Ak，y∈Ajand j≥k+2，so we have|y-z|～|y|.

Similar to（3.4），we get

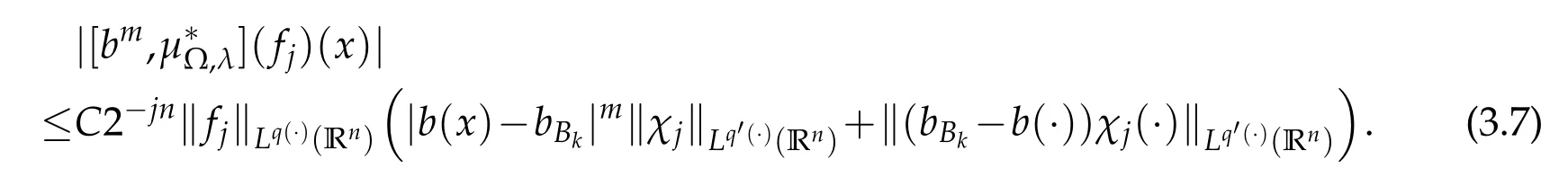
By Lemma 1.3，Lemma 1.4 and Lemma 3.2，we have

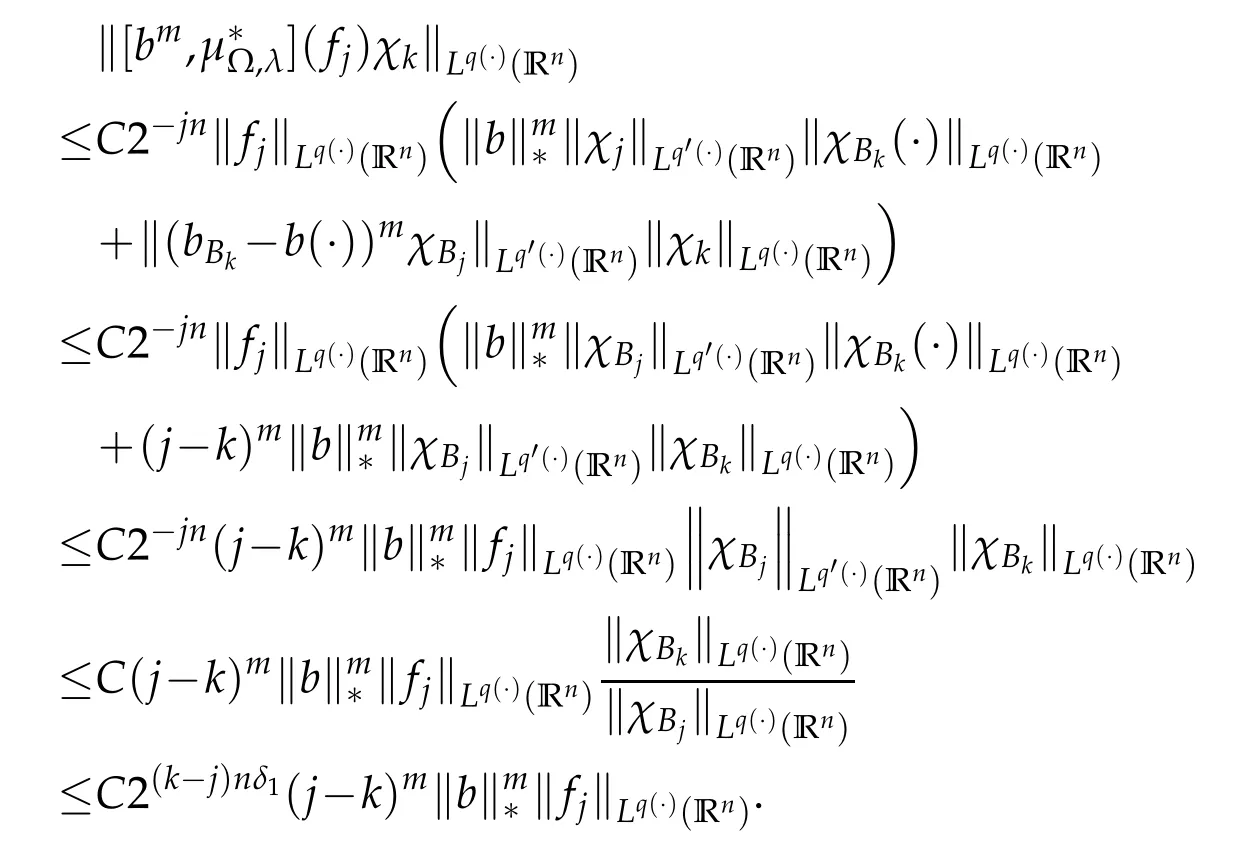
Thus we obtain

If 1＜p＜∞，take 1/p+1/p′=1.Since nδ1+α＞0，by the H¨older inequality we have

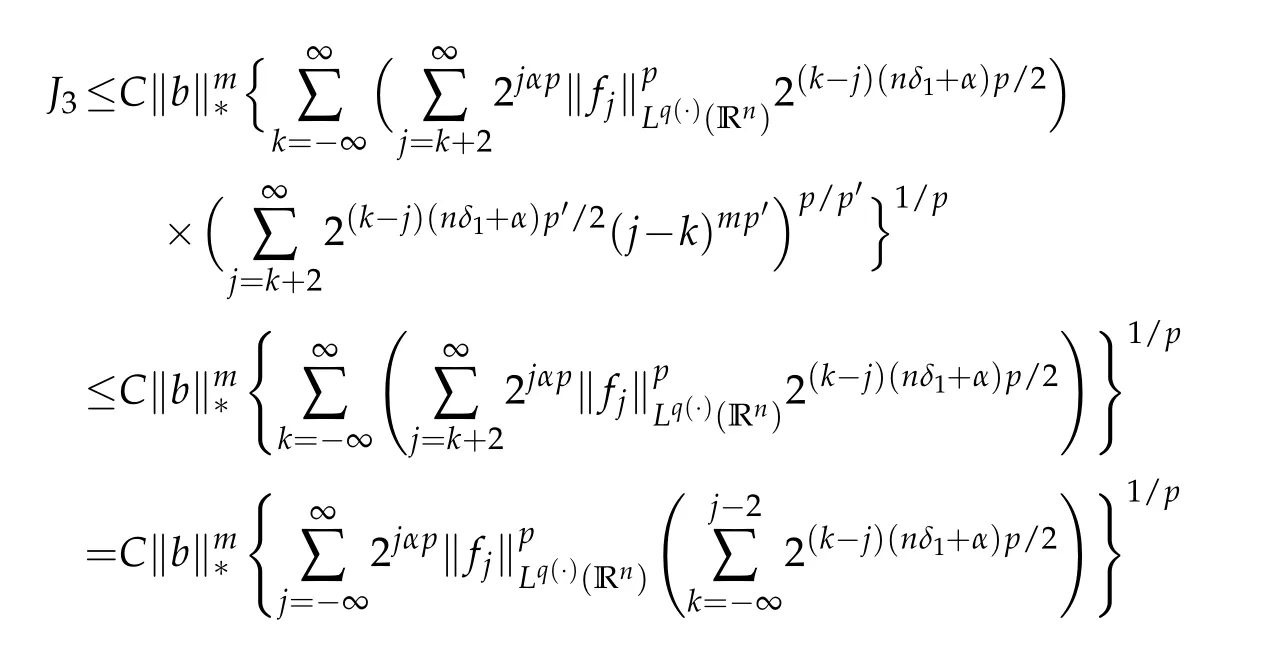
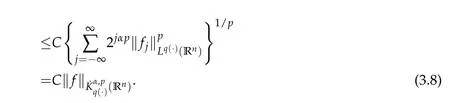
If 0＜p≤1，then we have

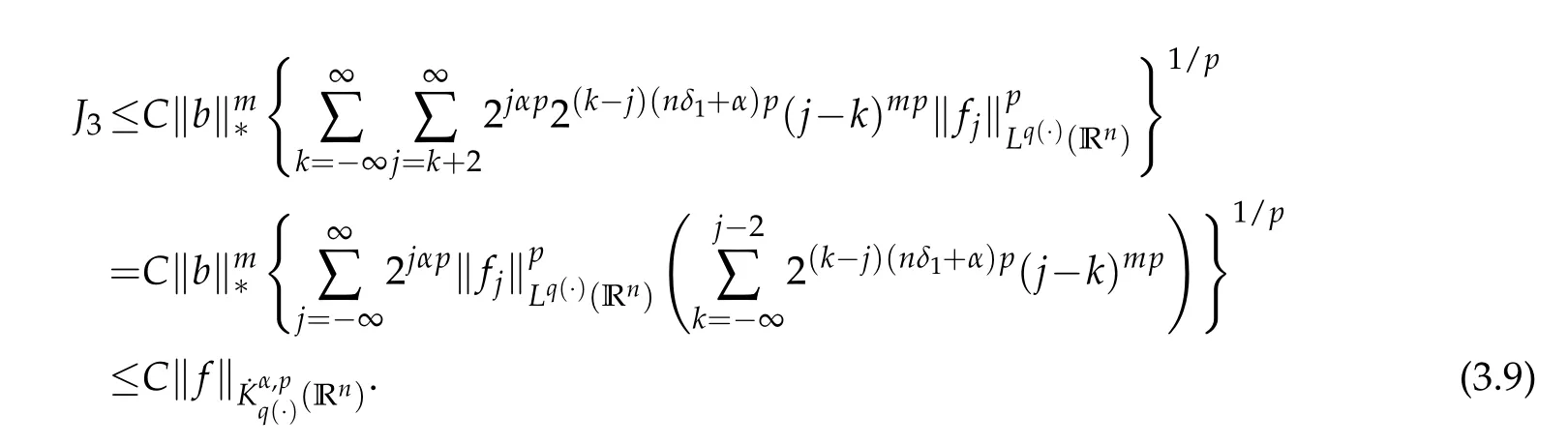
Therefore，by（3.1），（3.2），（3.5），（3.6），（3.8），（3.9），we complete the proof of Theorem 3.1.

Since［bm，µΩ，S］（f）（x）≤Cλ［bm，µ∗Ω，λ］（f）（x），we easily obtain the following theorem.

Acknowledgments

The authors are very grateful to the referees for their valuable comments.

［1］C.Capone，D.Cruz-Uribe and A.Fiorenza，The fractional maximal operator and fractional integrals on variable Lpspaces，Rev.Mat.Iberoamericana，23（2007），743-770.

［2］D.Cruz-Uribe，A.Fiorenza，J.M.Martell and C.P´erez，The boundedness of classical operators on variable Lpspaces，Ann.Acad.Sci.Fen.Math.，31（2006），239-264.

［3］Y.Ding，D.Fan and Y.Pan，Weighted boundedness for a class of rough Marcinkiewicz integral，Indiana Univ.Math.J.，48（1999），1037-1055.

［4］Y.Ding，S.Luand K.Yabuta，On commutators of Marcinkiewiczintegrals with rough kernel，J.Math.Anal.Appl.，275（2002），60-68.

［5］M.Izuki，Boundedness of sublinear operators on Herz spaces with variable exponent and application to wavelet characterization，Anal.Math.，36（2010），33-50.

［6］M.Izuki，Boundedness of commutators on Herz spaces with variable exponent，Rend.del Circolo Mate.di Palermo，59（2010），199-213.

［7］O.Kov´aˇcik and J.R´akosn´ık，On spaces Lp（x）and Wk，p（x），Czechoslovak Math.J.，41（1991），592-618.

［8］Z.Liu and H.Wang，Boundedness of Marcinkiewicz integrals on Herz spaces with variable exponent，Jordan J.Math.Stat.，5（2012），223-239.

［9］H.Wang，Z.Fu and Z.Liu，Higher-order commutators of Marcinkiewicz integrals and fractional integrals on variable Lebesgue spaces，Acta Math.Sci.Ser.A China Ed.，32（2012），1092-1101.

［10］L.Wang and S.Tao，Parameterized Littlewood-Paley operators and their commutators on Lebesgue space with variable exponent，Anal.Theory Appl.，31（2015），13-24.

.Email addresses:wanghb@sdut.edu.cn（H.Wang），wfapple123456@163.com（Y.Wu）

11 December 2015；Accepted（in revised version）11 April 2016