Some Approximation Properties of Certain q-Baskakov-Beta Operators

Ruirui Liu，Xiaomin Huand Huating Wu

InstituteofMathematics，HangzhouDianziUniversity，Hangzhou，Zhejiang310018，China



Some Approximation Properties of Certain q-Baskakov-Beta Operators

Ruirui Liu，Xiaomin Hu∗and Huating Wu

InstituteofMathematics，HangzhouDianziUniversity，Hangzhou，Zhejiang310018，China

.In this paper，we propose the q analogue of modified Baskakov-Beta operators.The Voronovskaja type theorem and some direct results for the above operators are discussed.The rate of convergence and weighted approximation by the operators are studied.

q-Baskakov-Beta operators，rate of convergence，weighted approximation.

AMS Subject Classifications:41A25，41A35

1　Introduction

In recent years，the application of q calculus is the most interesting areas of research in the approximation theory（e.g.，［1］）.Lupas¸［2］and Phillips［3］proposed generalizations of Bernstein polynomials based on the q-integers.More results on q-Bernstein operators were investigated（e.g.，［4，5］）.Gupta and Aral［6，7］proposed certain q-analogues of the Baskakov operators and studied some approximation properties of q-Baskakov operators.

In approximation theory the Durrmeyer type integral modification of certain discrete operators is also an active area of research.Cai［8］investigated the convergence of modification of Durrmeyer type q-Baskakov operators.Gupta and collaborators（see［9-13］，etc.）introducedseveralimportant q analoguesofdifferent Durrmeyertypeoperatorsand established interesting approximation results.In［14］，Gupta observed that the Baskakov operators by taking weight functions of Beta basis function give better approximatin results.Wang［15］also estimated asymptotic formula for Baskakov Beta operators in generalized form.

The aim of this paper is to study the approximation properties of cerntain generalization of Baskakov Beta operators，based on q-integer.We first recall some concept ofq-calculus，which can be found in［16］.In what follows，q is a real number satisfying 0＜q＜1.

For k∈N，the q integer and q factorial are given by

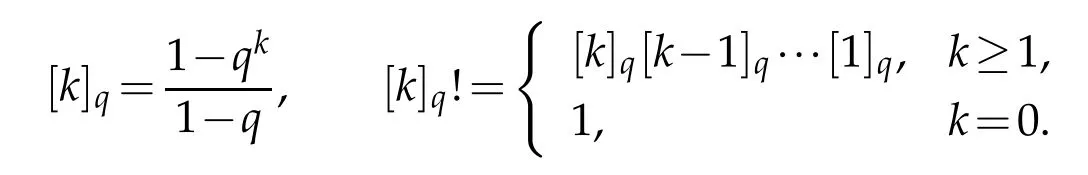
The q-binomial coefficients are defined as

The q-Pochhammer symbol is defined as

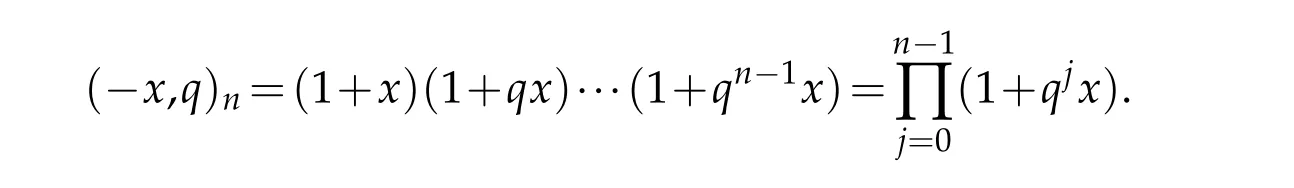
The q-Jackson integrals and the q-improper integrals are defined as（see［17，18］）

and provided the sum converge absolutely.

The q-Gamma integral（see［19］）is defined by

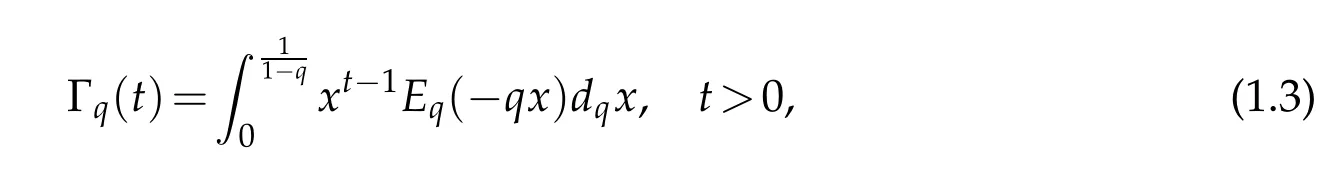
where

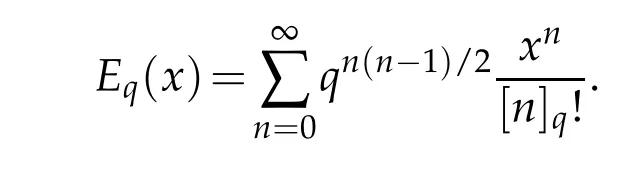
Also Γq（t+1）=［t］qΓq（t），Γq（1）=1.

The q-Beta integral（see［19］）is defined by

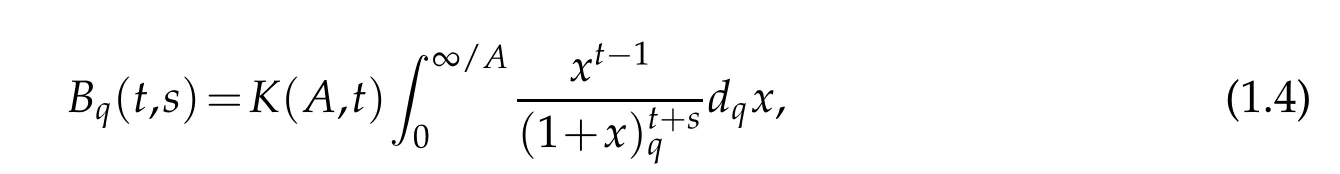
whereIt was observed in that K（x，t）is a q-constant，i.e.，K（qx，t）=K（x，t）.In particular for any positive integer n，one has

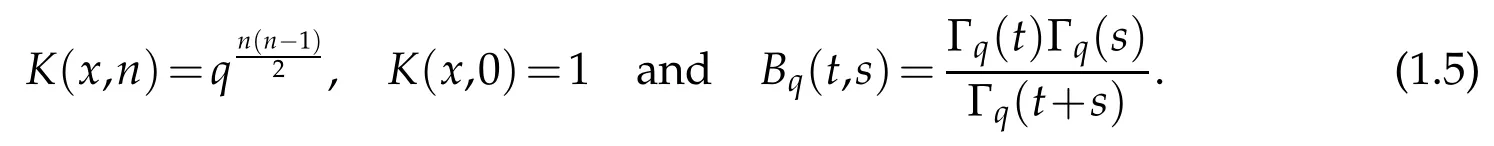
The q-derivative Dqis given by

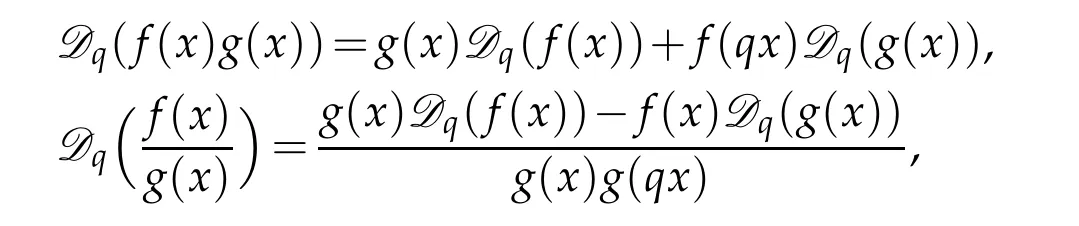
Recently，Aral and Gupta［21］introduced a different q-generalization of the classical Baskakov operators.For f∈C［0，∞），q＞0 and each positive integer n，the operators introduced in［21］are defined as

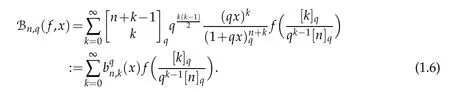
We denote by CB［0，∞）the space of all real valued continuous bounded funtion f defined on［0，∞），endowed with the norm

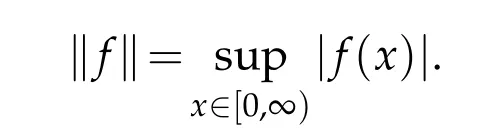
For every n∈N，f（x）∈CB［0，∞），the certain q-Baskakov Beta operators D∗n，q（f，x）are defined as

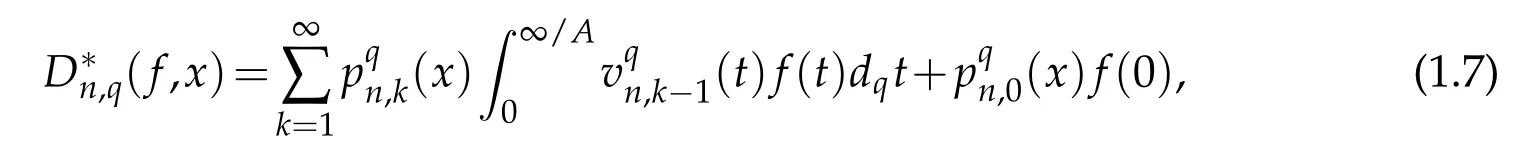
where x∈［0，∞），and

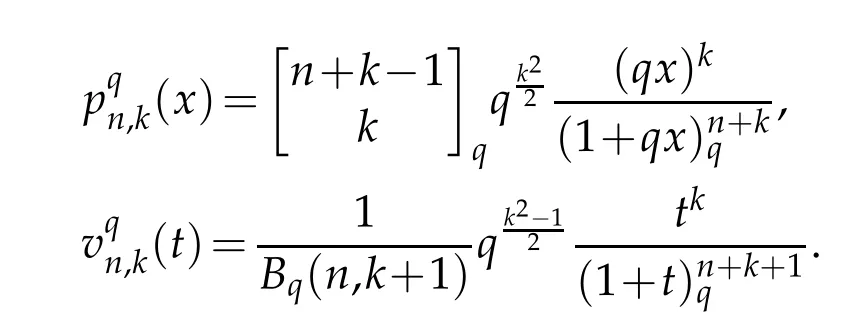
The above q-analogues of Baskakov Beta operators are defined on q∈（0，1）.And these operators are linear and reproduce only the constant functions.The present paper is organized as follows:in the first section，we present the basic notations and the definitions of q analogues of Baskakov Beta operators.In the second section，we give the moment estimates and establish the recurrence relation for the moments of the operators by the q-derivatives.In Section three we give the basic convergence theorem and Voronovskaja type theorem.Section four and five，we study the local approximation and the rate of convergence of the operators.And we also estimate the weighted approximation properties.

2　Moment estimates

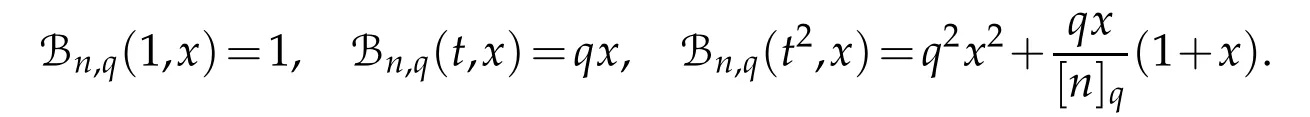
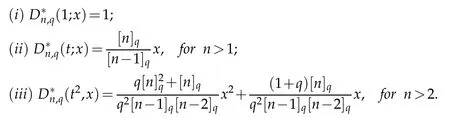
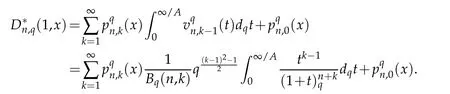
Using（1.1），（1.4），（1.5）and Lemma 2.1，we may write

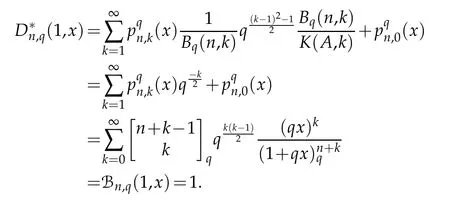
Similarly，

From Lemma 2.1，we get

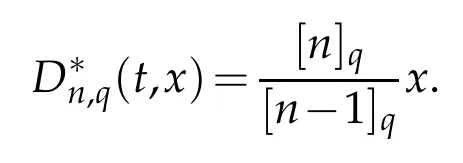
Finally，

Using

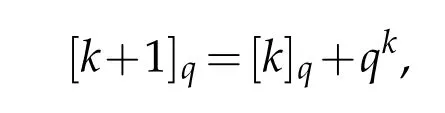
we have

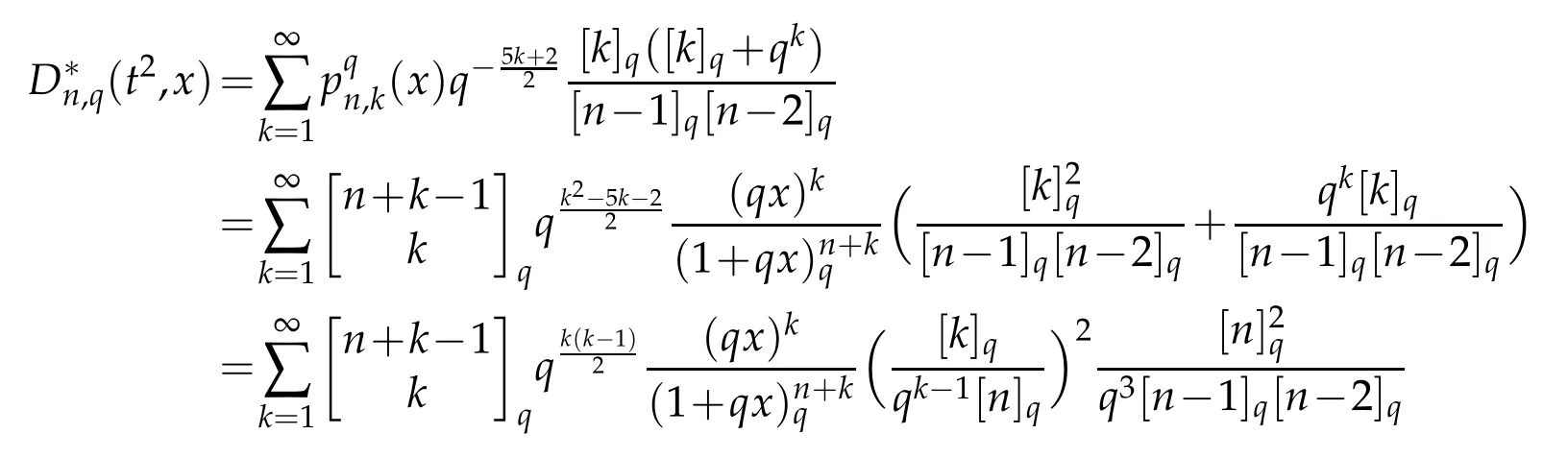
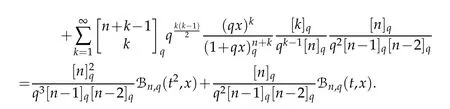
Again using Lemma 2.1，we obtain

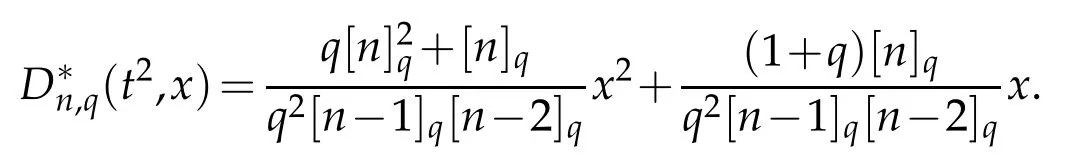
Thus，we complete the proof.

Remark 2.1.Let n＞2 be a given number.For every 0＜q＜1，from Lemma 2.1 we have

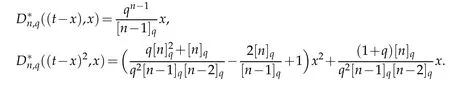
Proposition 2.1（see［7］）.For n，k≥0，we have

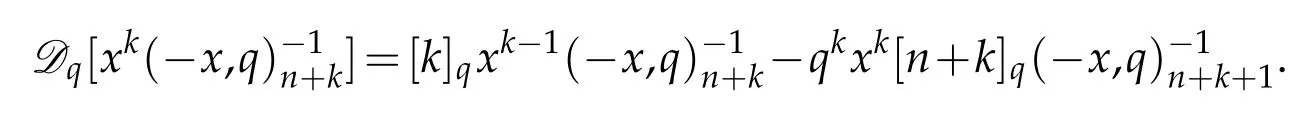
Remark 2.2.For n，k∈N，from Proposition 2.1，we have

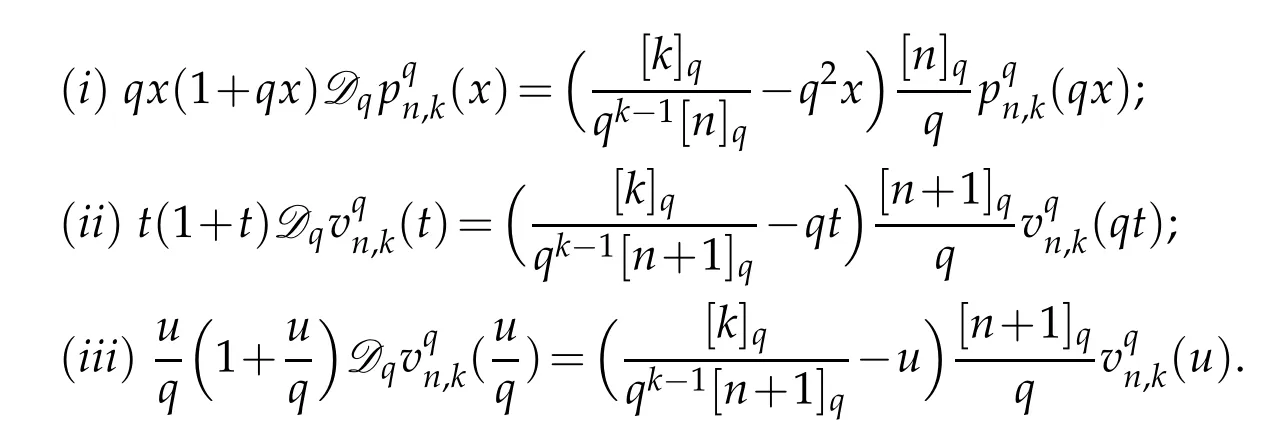
Proposition 2.2.If we define the mth order（m∈N）moment as

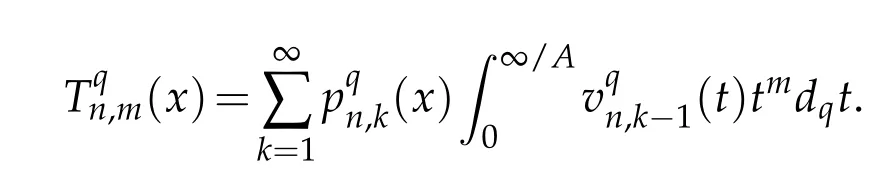
Then，for n＞m+2 the following recurrence relation holds

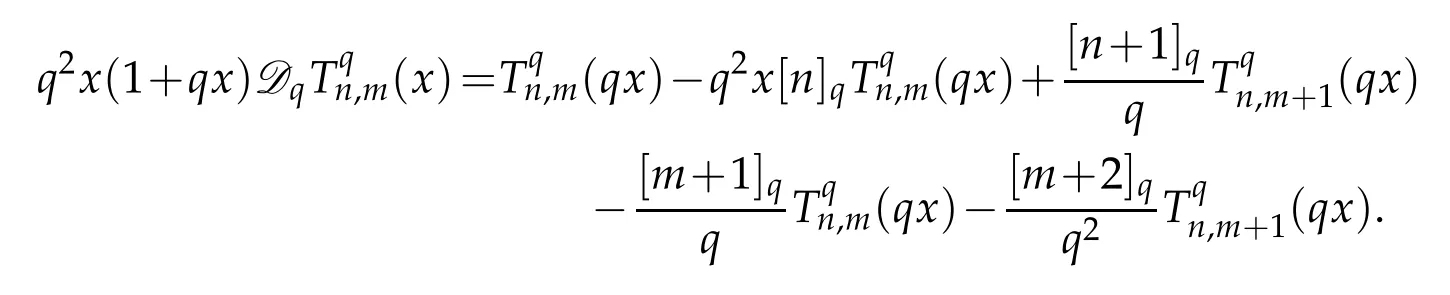
Since［k］q=［k-1］q+qk-1，we obtain

Let us consider

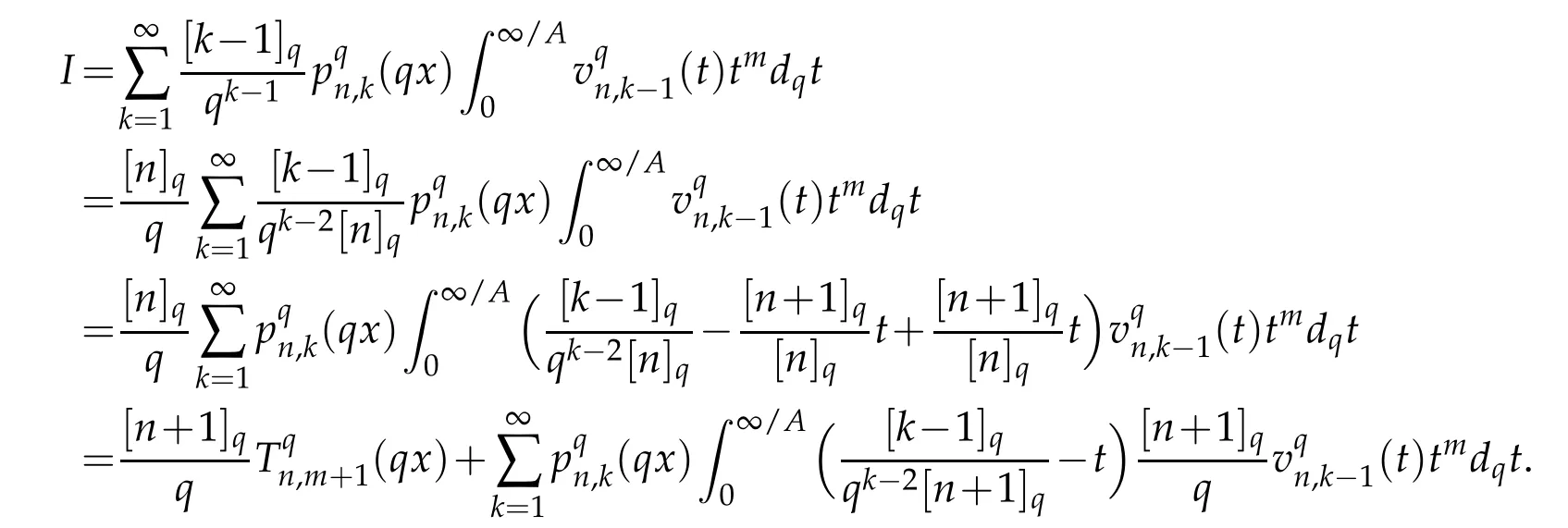
Again using Remark 2.2（iii），we get

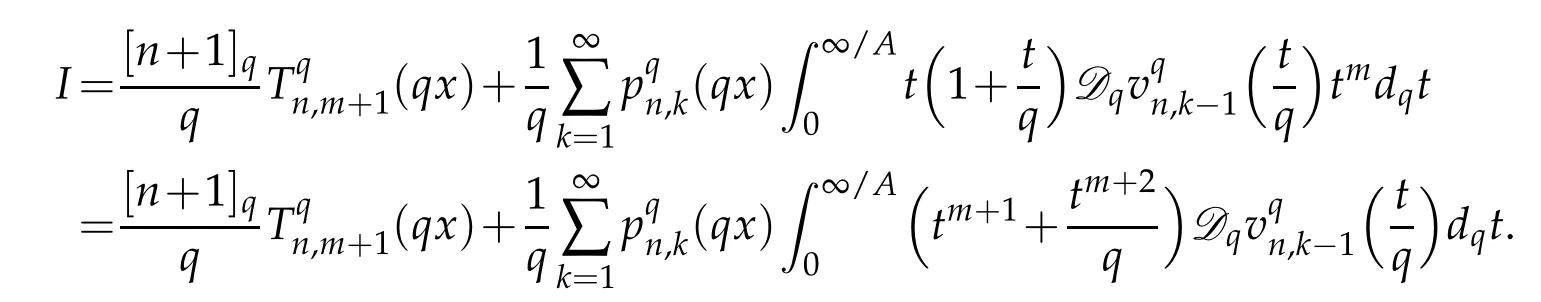
Using the q-intergal by parts

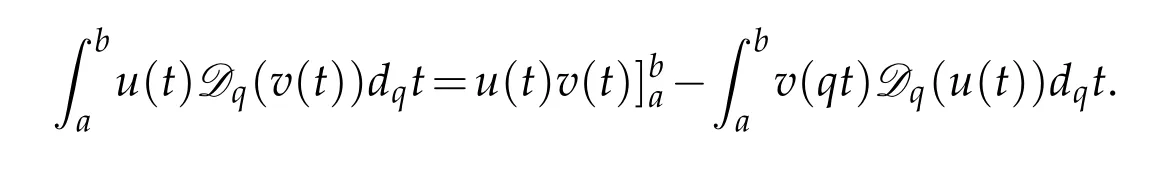
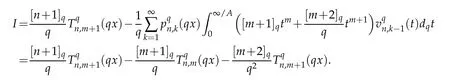
Finally，we have

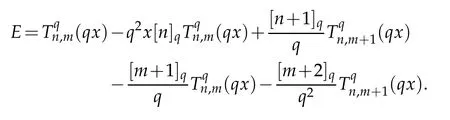
This completes the proof of the recurrence relation.

Lemma 2.3.For all f∈CB［0，∞），n=1，2，···，and q∈（0，1），we have

在辽宁，监管部门要求银行将“公平信贷”原则贯穿信贷管理全程，从业务受理、客户评级、放款约束、贷后管理等方面，检查是否存在可能影响公平信贷的政策，取消不合理的条款、要求和做法。在重庆，监管部门划分机构、片区，组织机构负责人和一线客户经理，对全市6000余家民营工业企业进行全覆盖式走访、回访，对民企广泛关注的困难和问题拿出切实举措，目前已现场为民企解决各类融资问题30个，落实资金24.6亿元。在浙江，监管部门组织银行对全省授信10亿元以上企业进行筛选，探索建立优质企业“白名单”，对暂时遇到困难但仍有发展前景的企业，主动开展帮扶，助力企业提前做好债券兑付安排，推动市场化法治化债转股落地。

Proof.For x∈［0，∞），we get

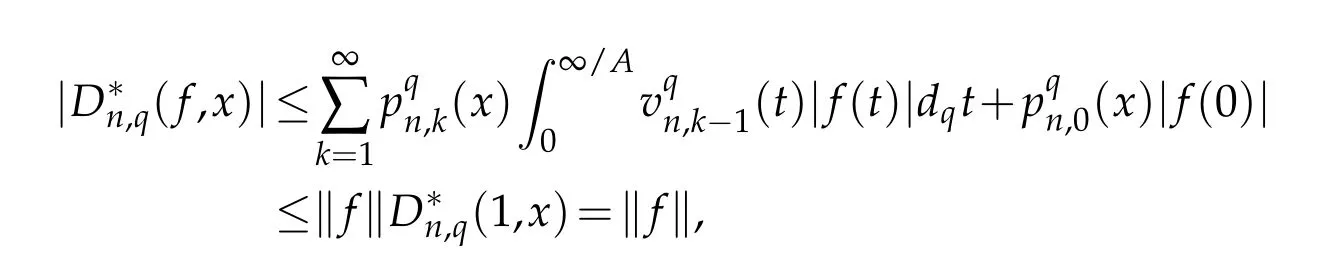
which completes the proof.

3　Direct theorems

Theorem 3.1.Let qn∈（0，1）.Then the sequence｛D∗n，qn（f）｝converges to f uniformly on［0，A］，A＞0 for each f∈CB［0，∞）if and only if limn→∞qn=1.

Theorem 3.2（Voronovskaja type theorem）.Assume that qn∈（0，1），qn→1 and qnn→a as n→∞.For any f∈CB［0，∞），if f′，f′exists on［0，∞），the following equality holds

uniformly on any［0，A］，A＞0.

Proof.Let x∈［0，∞）be arbitrary but fixed.From the Taylor's theorem，we may write

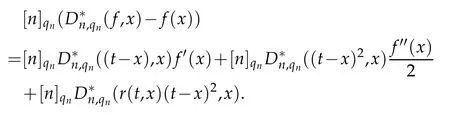
In view of Remark 2.1，we have

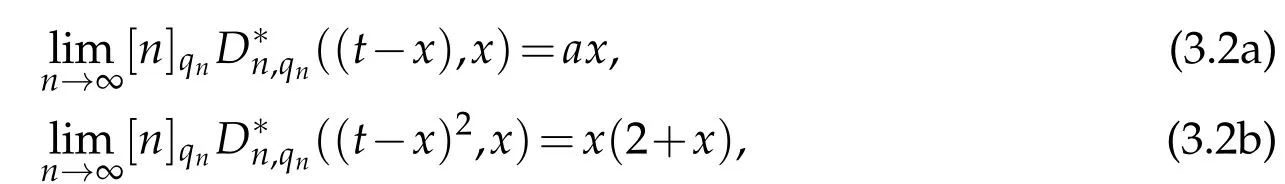
uniformly in x∈［0，A］.

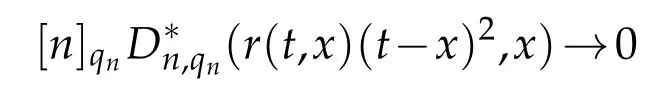
uniformly in x∈［0，A］，when n→∞.By the Cauchy-Schwartz inequality，we have

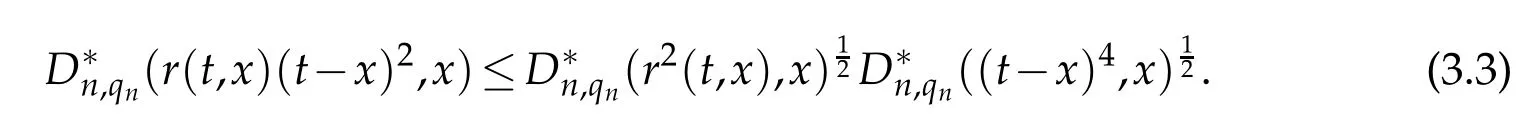
We observe that r2（x，x）=0 and r2（·，x）=0∈CB［0，∞）.Then it follows from Theorem 3.1 that

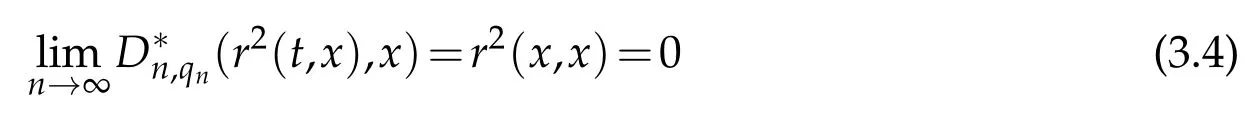
uniformly in x∈［0，A］.Now from（3.3），（3.4）we getNow combining（3.1）-（3.5），we get the required result.

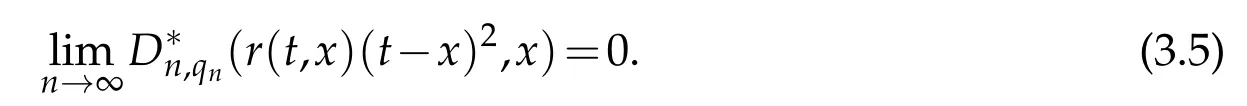
Let δ＞0 and W2∞=｛g∈CB［0，∞）:g′，g′∈CB［0，∞）｝.For f∈CB［0，∞），we consider the following K-function:

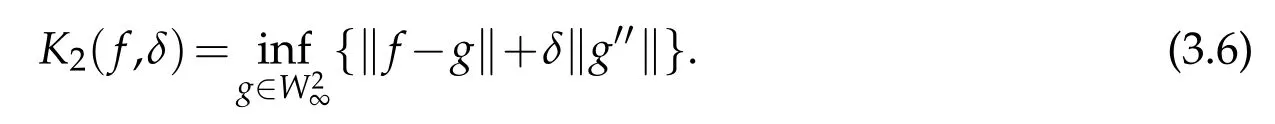
By seeing［22］，there exist an absolute constant C＞0 such that

where

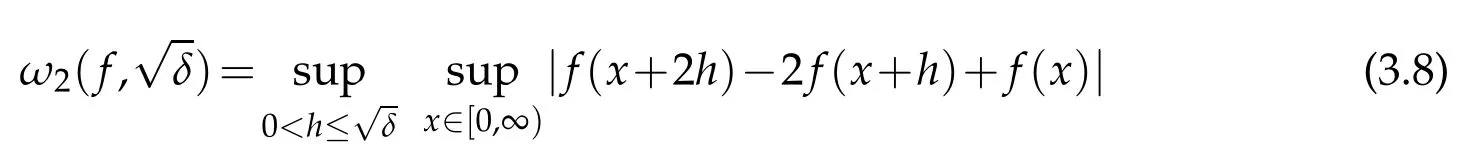
is the second order modulus of continuity.The usual modulus of continuity for f∈CB［0，∞）is given by

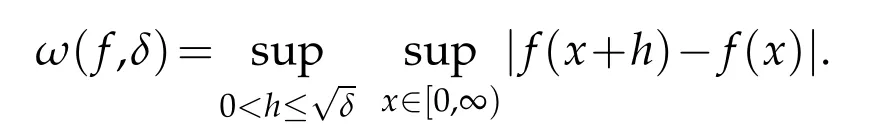
Theorem 3.3.Let f∈CB［0，∞）and q∈（0，1），then for every x∈［0，∞），there exists an absolute constant C＞0，such that

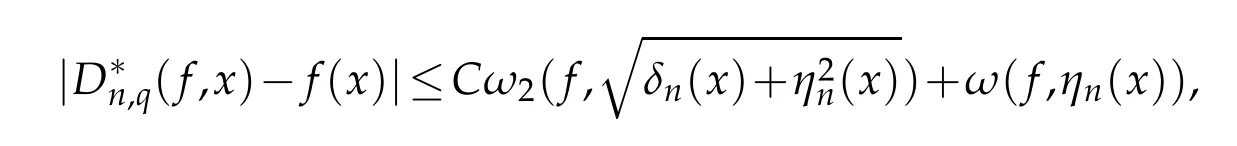
where

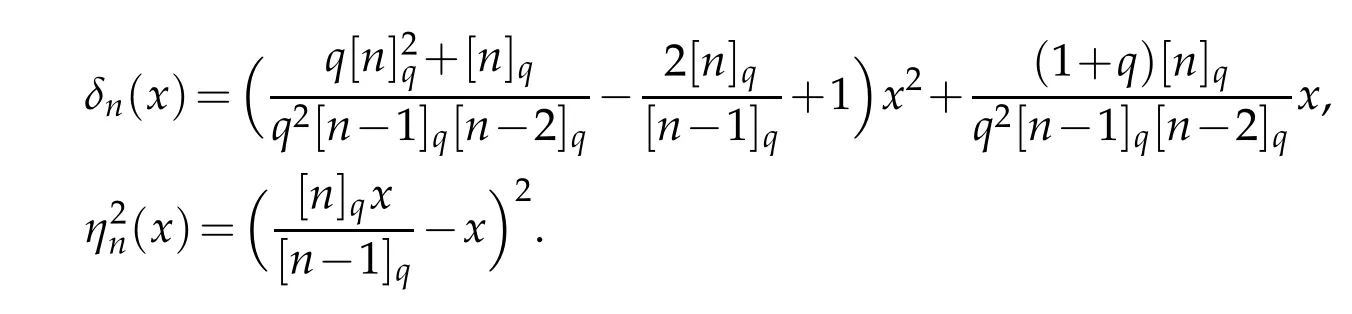
Proof.we define

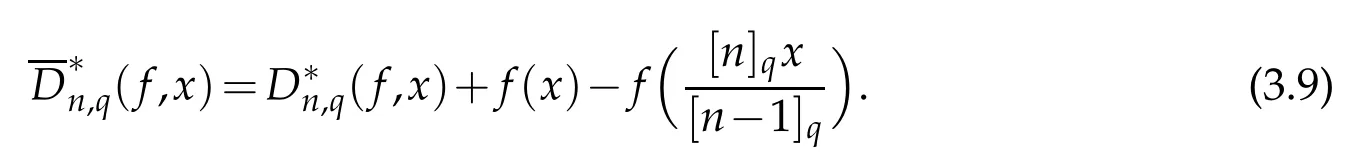
From Lemma 2.1，we obtain

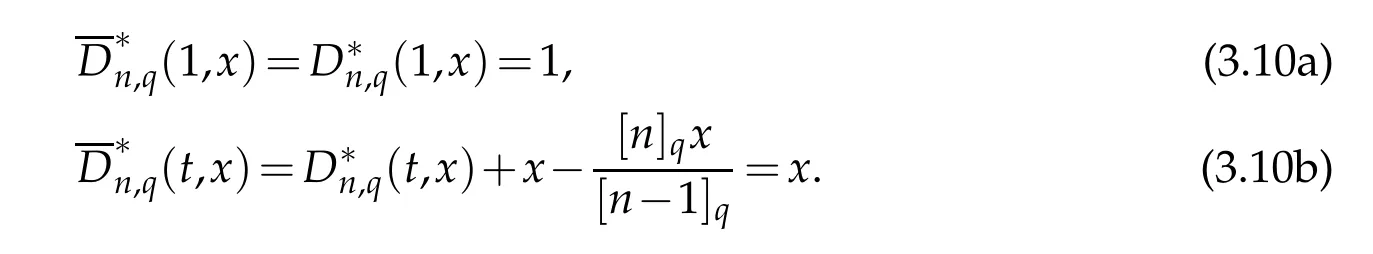
Let g∈W2∞，using Taylor's formula，we have

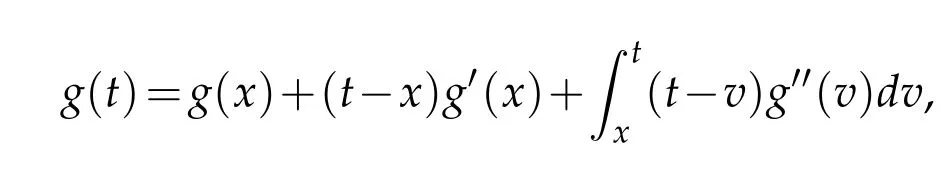
We get

Which implies that

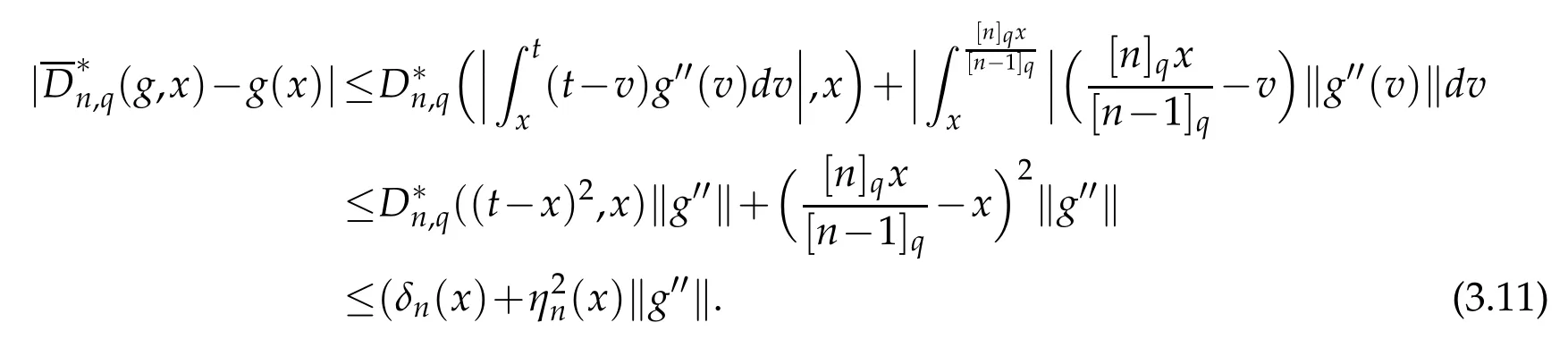
In view of（3.9），we obtain

From Lemma 2.3，we get

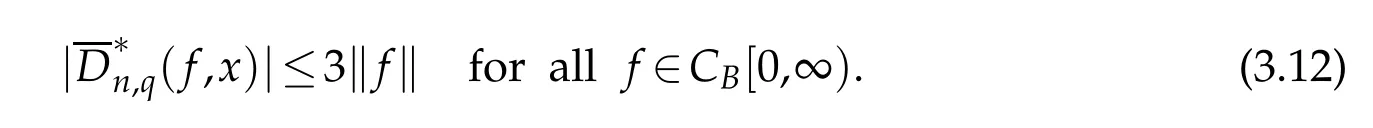
Using（3.11），（3.12）in（3.9），we obtain

Taking the infimum on the right hand side over all g∈W2∞and applying（3.6）we get

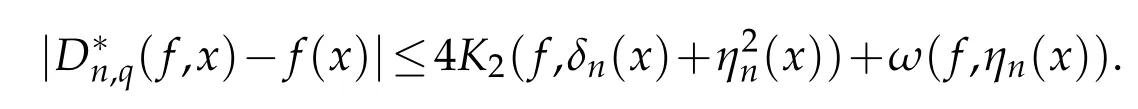
Using（3.7），we have

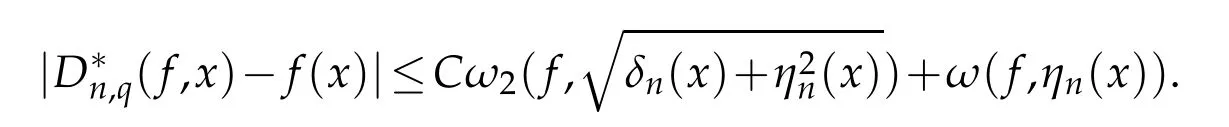
This completes the proof.

4　Rate of convergence

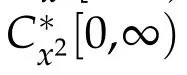
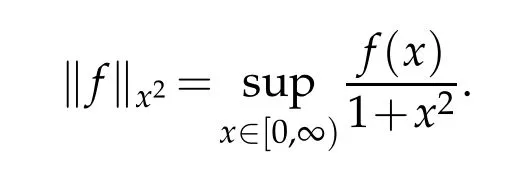
The usual modulus of continuity of f on the closed interval［0，a］，a＞0 is

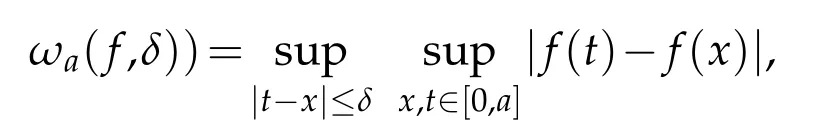
we know that for a function f∈Cx2［0，∞），the modulus of continuity ωa（f，δ））tends to zero.

Now we give a rate of convergence theorem for the operators D∗n，q.

Theorem 4.1.Let q∈（0，1）and ωa+1（f，δ））be its modulus of continuity on the finite interval［0，a+1］⊂［0，∞），where a＞0，then for every f∈Cx2［0，∞），we have

where

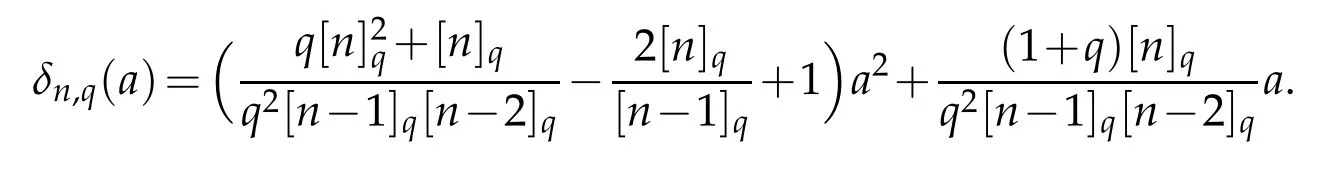
Proof.For x∈［0，a］and t＞a+1，since t-x＞1，we have

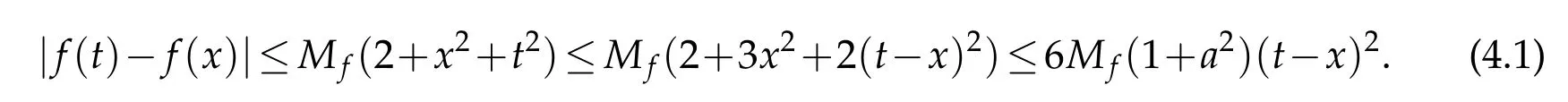
For x∈［0，a］and t≤a+1，we get

with δ＞0.

From（4.1）and（4.2），we can write

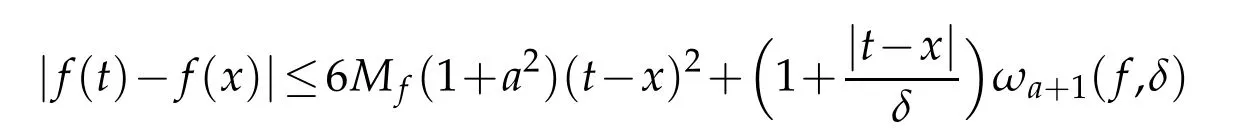
for x∈［0，a］and t＞0.Hence，by Schwarz's inequality we have

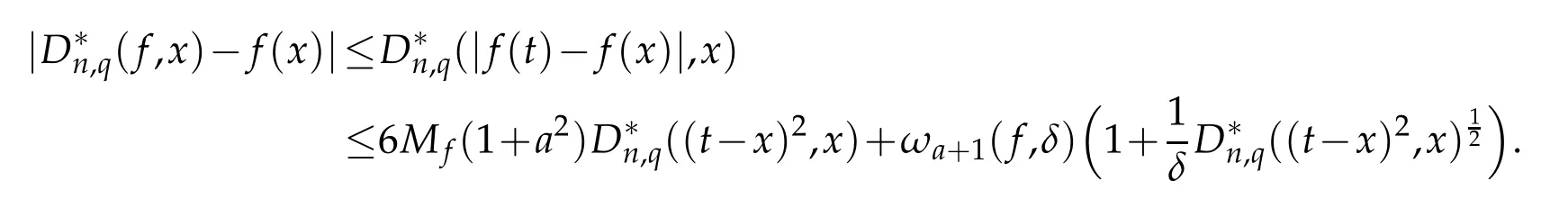
Using Remark 2.1，for every q∈（0，1）and x∈［0，a］，we obtain

where

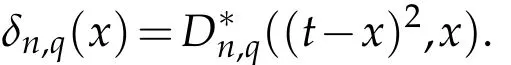
By taking

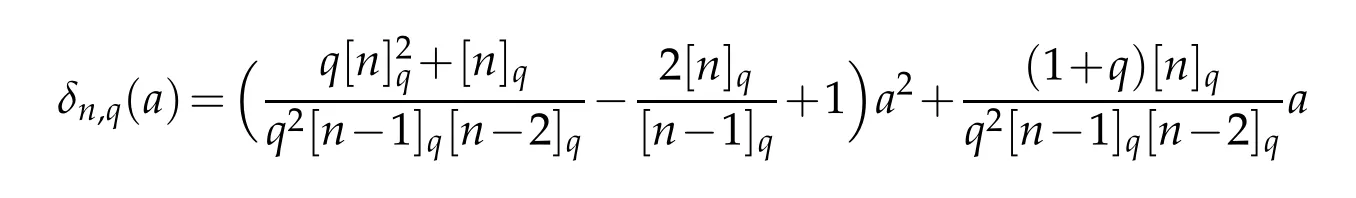
and

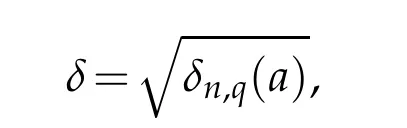
we get the assertion of our theorem.

5　Weighted approximation

We shall discuss the weighted approximation theorems in this section，and we assume that｛qn｝is a sequence such that qn∈（0，1）and qn→1 as n→∞.

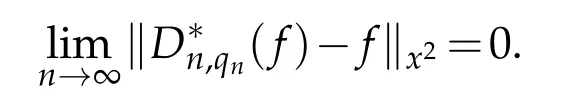
Proof.Using the Korovkin's theorem in［23］，it is sufficient to verify the following three conditions

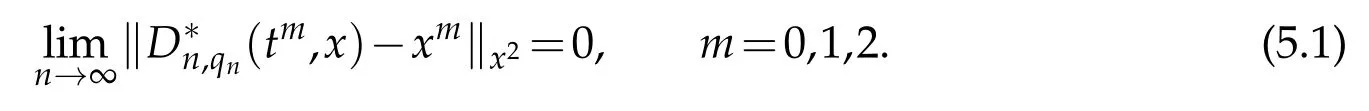
Since

the first condition of（5.1）is fulfilled for m=0.

By Lemma 2.2，we have for n＞1

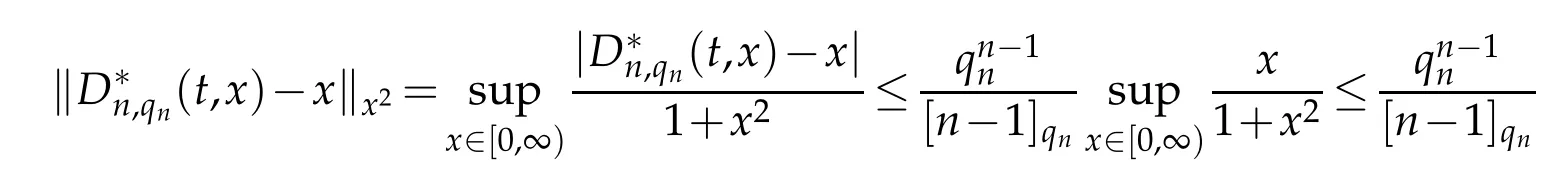
and the second condition of（5.1）holds for m=1 as n→∞.

Again using Lemma 2.2，we can write for n＞2

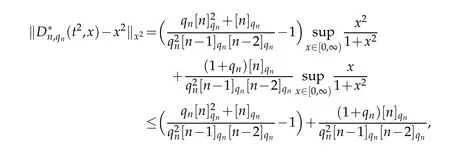
which implies that

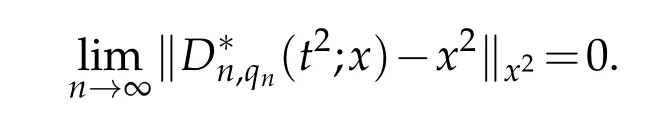
Thus the proof is completed.

Next we give the theorem to approximation all function in Cx2［0，∞）in the following.This type of result for locally integrable functions is discussed in［24］.

Theorem 5.2.For each f∈Cx2［0，∞）and α＞0，we have

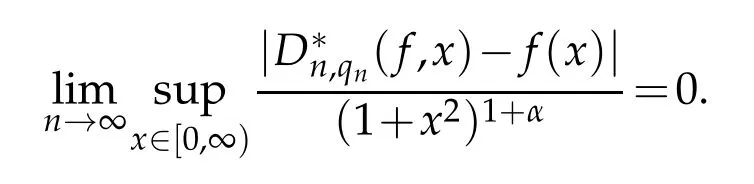
Proof.Let x0∈［0，∞）be arbitrary but fixed，we have

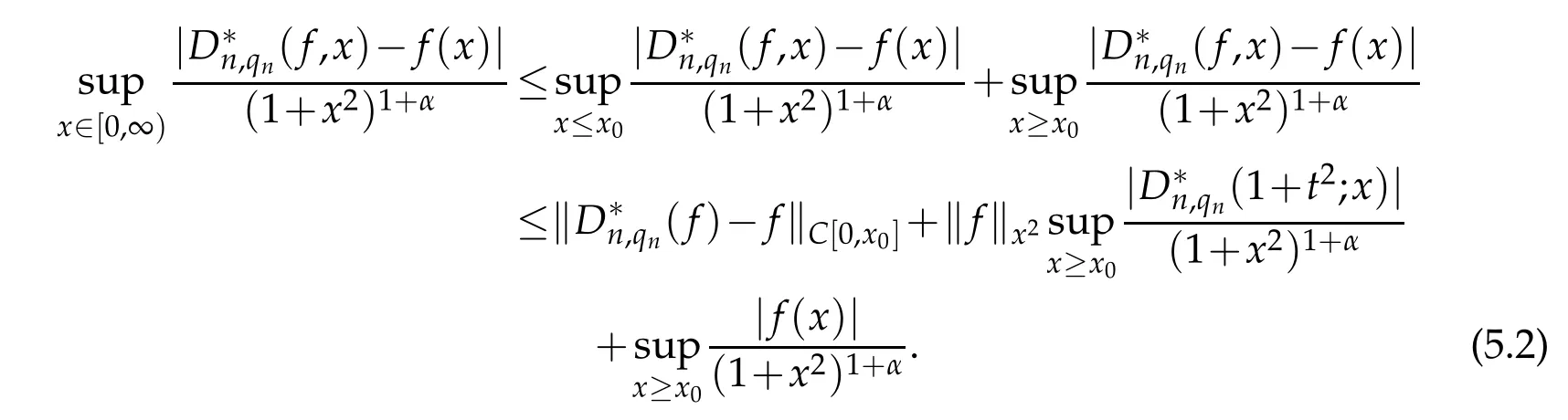
Since

we get

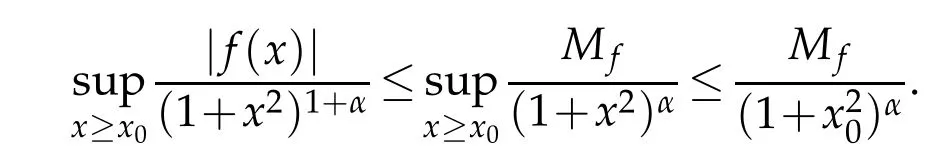
Let ε＞0 be arbitrary，we choose x0to be so large that

In view of Theorem 3.1，we obtain

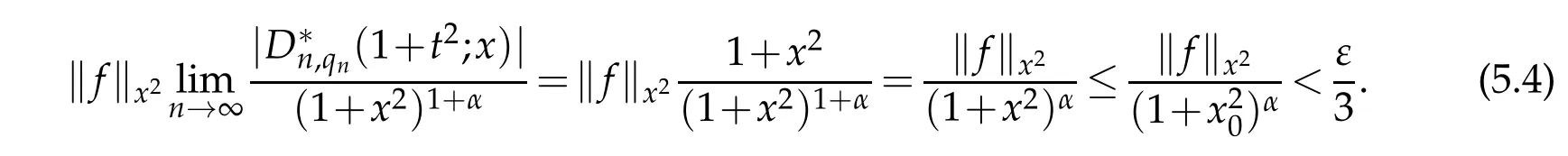
Now using Theorem 4.1，the first term of the inequality（5.2）implies that

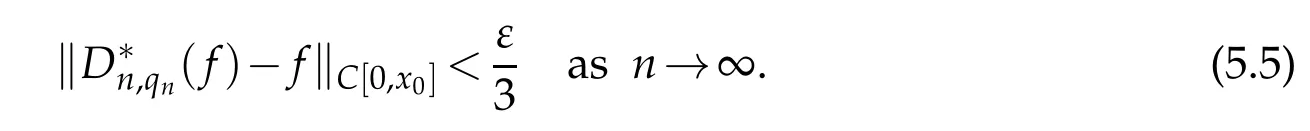
Combining（5.3）-（5.5），we get the desired result.

Acknowledgments

The authors would like to express their sincere gratitude to the referees for many helpful comments on this paper.

［1］C.Zhao and Q.B.Cai，Approximation properties of a kind of q-Beta operators，J.Comput. Anal.Appl.，18（2015），291-298.

［2］A.Lupas¸，A q-Analogue of the Bernstein Operator，Seminar on Numerical and Statistical Calculus，University of Cluj-Napoca，9（1987），85-92.

［3］G.M.Phillips，Bernstein polynomials based on the q-integers，Ann.Numer.Math.，4（1996），511-518.

［4］S.Ostrovska，q-Bernstein polynomials and their iterates，J.Approx.Theory，123（2003），232-255.

［5］H.P.Wang，Voronovskaya-type formulas and saturation of convergence for q-Bernstein polynomials for 0＜q＜1，J.Approx.Theory，145（2007），182-195.

［6］A.Aral and V.Gupta，On q-Baskakov type operators，Demonstratio Mathematica，42（2009），109-122.

［7］A.Aral and V.Gupta，Generalized q Baskakov operators，Math.Slovaca.，61（2011），619-634.

［8］Q.B.Cai and X.M.Zeng，Convergence of modification of Durrmeyer type q-Baskakov operators，Georgian Math.J.，19（2012），49-61.

［9］V.Gupta，On certain type Durrmeyer type q Baskakov operators，Ann.Univ.Ferrara.，56（2010），295-303.

［10］X.M.Zeng，V.Gupta and O.Agratini，Approximation by B´ezier Variant of the Baskakov-Kantorovich operators in the case 0＜α＜1，Rocky Mountain J.Math.，44（2014），317-327.

［11］V.Gupta and A.Aral，Approximation by q Baskakov Beta operators，Acta Mathematicae Applicatae Sinica，English Series，27（2011），569-580.

［12］V.Gupta and H.Sharma，Recurrence formula and better approximation for q Durrmeyer operators，Lobachevskii J.Math.，32（2011），140-145.

［13］V.Gupta and H.Wang，The rate of convergence of q-Durrmeyer operators for 0＜q＜1，Math. Methods Appl.Sci.，31（2008），1946-1955.

［14］V.Gupta，A note on modified Baskakov type operators，Approx.Theory Appl.，10（1994），74-78.

［15］Li Wang，The Voronovskaja type expansion formula of the modified Baskakov-Beta operators，J.Baoji Univ.Arts Sci.Nat.Sci.，25（2005），94-97.

［16］V.G.Kac and P.Cheung，Quantum Calculus，Springer-Verlag，New York，2002.

［17］F.H.Jackson，On a q-definite integrals，Quart.J.Pure Appl.Math.，41（1910），193-203.

［18］T.H.Koornwinder，q-specialfunctions，FacultyofMathematicsandComputerScience，Plantage Muidergracht，24（2005），1018.

［19］A.De Sole and V.G.Kac，On integral representationof q-gamma and q-beta functions，Rend. Mat.Accad.Lincei，16（2005），11-29.

［20］T.Ernst，The History of q-Calculus and a New Method，Preprint，2001.

［21］V.Gupta and A.Aral，Approximation by q Baskakov Beta operators，Acta Mathematicae Applicatae Sinica，English Series，27（2011），569-580.

［22］R.A.DeVore and G.G.Lorentz，Constructive Approximation，Springer，Berlin，1993.

［23］A.D.Gadzhiev，Theorems of the type of PP Korovkin type theorems，Mat.Zametki，20（1976），781-786.

［24］A.D.Gadjiev，R.O.EfendiyevandE.Ibikli，On Korovkin type theoremin the spaceof locally integrable functions，Czech.Math.J.，53（2003），45-53.

.Email addresses:Rrui Liu@126.com（R.R.Liu），mathhuxm@163.com（X.M.Hu），1182740572@qq.com（H.T.Wu）

22 March 2016；Accepted（in revised version）7 June 2016