On Growth of Polynomials with Restricted Zeros
2016-10-24AbdullahMirandParrey
Abdullah Mirand G.N.Parrey
1Department of Mathematics,University of Kashmir,Srinagar,190006,India
2Department of Mathematics,Islamia College of Science and Commerce,Srinagar,190002,India
On Growth of Polynomials with Restricted Zeros
Abdullah Mir∗and G.N.Parrey
1Department of Mathematics,University of Kashmir,Srinagar,190006,India
2Department of Mathematics,Islamia College of Science and Commerce,Srinagar,190002,India
.Let P(z)be a polynomial of degree n which does not vanish in|z|<k,k≥1. It is known that for each 0≤s<n and 1≤R≤k,In this paper,we obtain certain extensions and refinements of this inequality by involving binomial coefficients and some of the coefficients of the polynomial P(z).
Polynomial,maximum modulus princple,zeros.
AMS Subject Classifications:30A10,30C10,30C15
1 Introduction and statement of results
Let Pnbe the class of polynomials
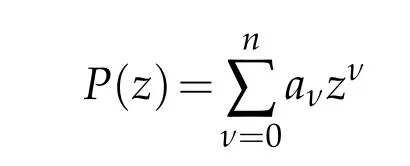
of degree n,z being a complex variable and P(s)(z)be its sthderivative.For P∈Pn,let M(P,R)=max|z|=R|P(z)|.It is well known that

and
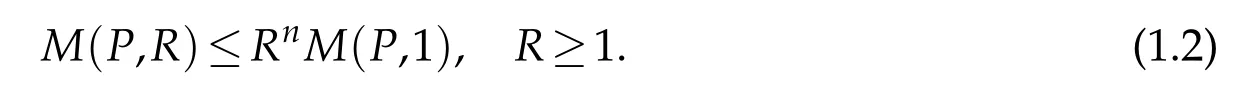
The inequality(1.1)is a famous result of S.Bernstein(for reference,see[9])whereas the inequality(1.2)is a simple consequence of Maximum Modulus Principle(see[8]).It was shown by Ankeny and Rivlin[1]that if P∈Pnand P(z)/=0 in|z|<1,then(1.2)can be replaced by

Recently,Jain[5]obtained a generalization of(1.3)by considering polynomials with no zeros in|z|<k,k≥1 and simultaneously have taken into consideration the sthderivative of the polynomial,(0≤s<n),instead of the polynomial itself.More precisely,he proved the following result.
Theorem 1.1.If P∈Pnand P(z)/=0 in|z|<k,k≥1,then for 0≤s<n,

and
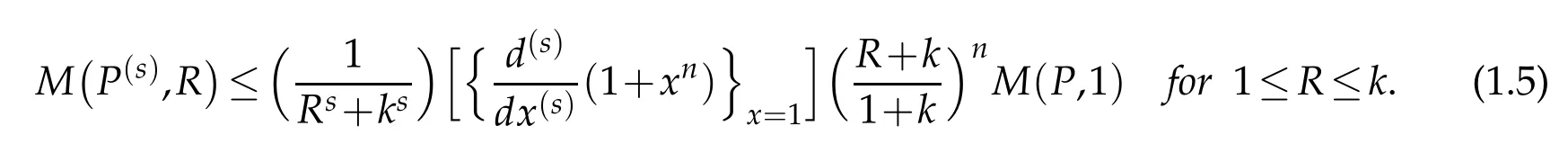
Equality holds in(1.4)(with k=1 and s=0)for P(z)=zn+1 and equality holds in(1.5)(with s=1)for P(z)=(z+k)n.
In this paper,we obtain certain extensions and refinements of the inequality(1.5)of the above theorem by involving binomial coefficients and some of the coefficients of polynomial P(z).More precisely,we prove
Theorem 1.2.If P∈Pnand P(z)/=0 in|z|<k,k>0,then for 0≤s<n and 0<r≤R≤k,we have
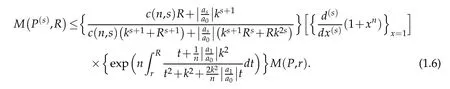
The result is best possible(with s=1)and equality in(1.6)holds for P(z)=(z+k)n.
Remark 1.1.Since if P(z)/=0 in|z|<k,k>0,then by Lemma 2.5(stated in Section 2),we have for 0≤s<n,

which can also be taken as equivalent to

Since R≤k,if we take t=R in(1.8),we get
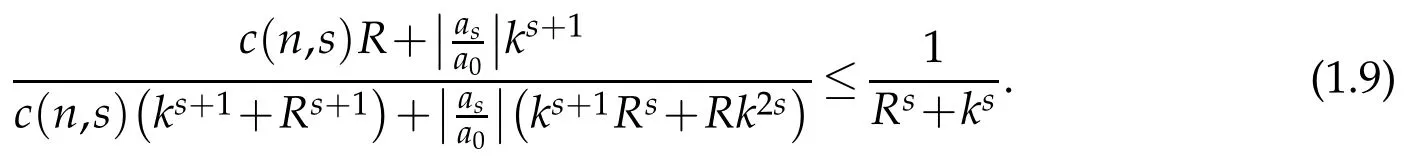
Also
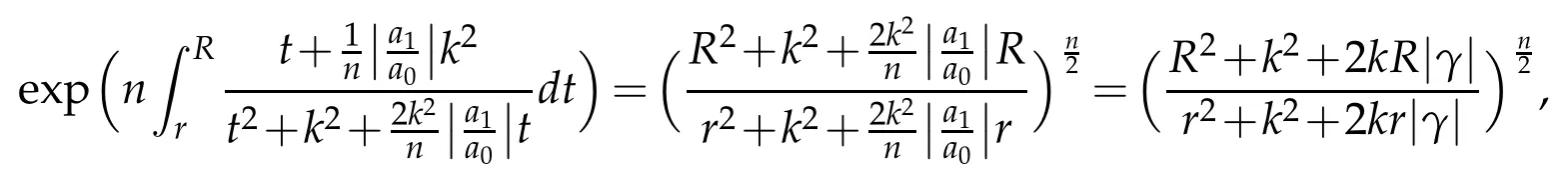
where γ=ka1/na0,has absolute value≤1,according to inequality(2.4)of Lemma 2.5.
Now as
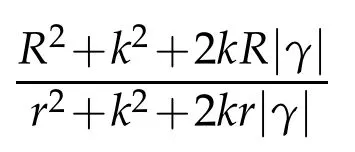
is an increasing function of|γ|in[0,1],hence

Combining(1.9)and(1.10),the following result immediately follows from Theorem 1.2. Corollary 1.1.If P∈Pnand P(z)/=0 in|z|<k,k>0,then for 0≤s<n and 0<r≤R≤k,we have
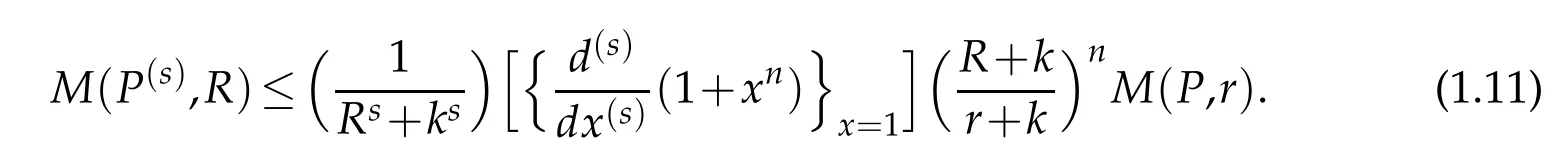
The result is best possible(with s=1)and equality in(1.11)holds for P(z)=(z+k)n. Remark 1.2.For r=1,Corollary 1.1 reduces to inequality(1.5).
Next we prove the following theorem which gives an improvement of Corollary 1.1(for 1≤s<n),which in turn as a special case provides an improvement and extension of the inequality(1.5).In fact,we prove
Theorem 1.3.If P∈Pnand P(z)/=0 in|z|<k,k>0,then for 1≤s<n and 0<r≤R≤k,we have

The result is best possible(with s=1)and equality in(1.12)holds for P(z)=(z+k)n. Remark 1.3.Since P(z)/=0 in|z|<k,k>0,therefore,for every λ with|λ|<1,it follows by Rouche's theorem that the polynomial P(z)-λm,has no zeros in|z|<k,k>0 and hence applying inequality(2.4)of Lemma 2.5(stated in Section 2),we get

If in(1.13),we choose the argument of λ suitably and note|a0|>m,from Lemma 2.3,we get
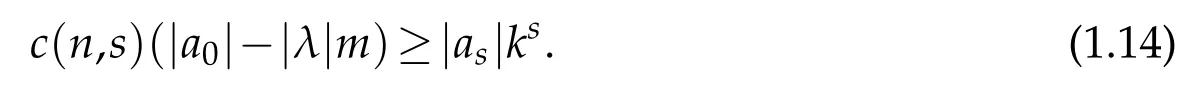
If we let|λ|→1 in(1.14),we get
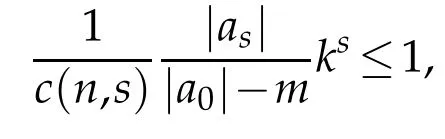
which further implies by using the same arguments as in Remark 1.1,that

and
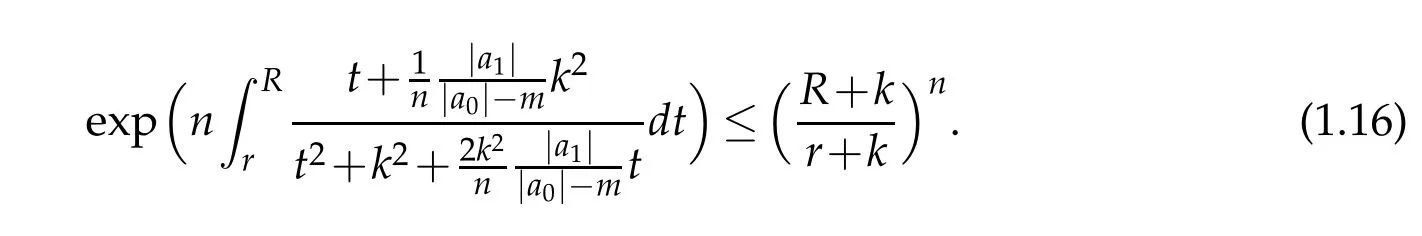
Now,using(1.15)and(1.16)in(1.12),the following improvement of Corollary 1.1(for 1≤s<n)and hence of inequality(1.5)immediately follows from Theorem 1.3.
Corollary 1.2.If P∈Pnand P(z)/=0 in|z|<k,k>0,then for 1≤s<n and 0<r≤R≤k,we have
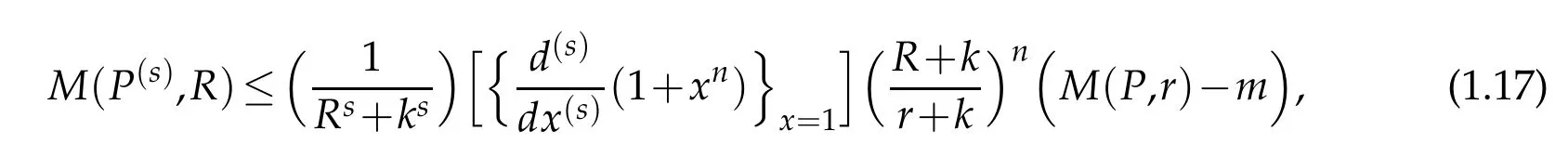
where m=min|z|=k|P(z)|.
The result is best possible(with s=1)and equality in(1.17)holds for P(z)=(z+k)n. Remark 1.4.The inequalities(1.11)and(1.17)were also recently proved by Mir(see[7]).
2 Lemmas
For the proof of these theorems,we need the following lemmas.
The first lemma is due to Aziz and Rather[2].
Lemma 2.1.If P∈Pnand P(z)/=0 in|z|<k,k≥1,then for 1≤s<n,we have
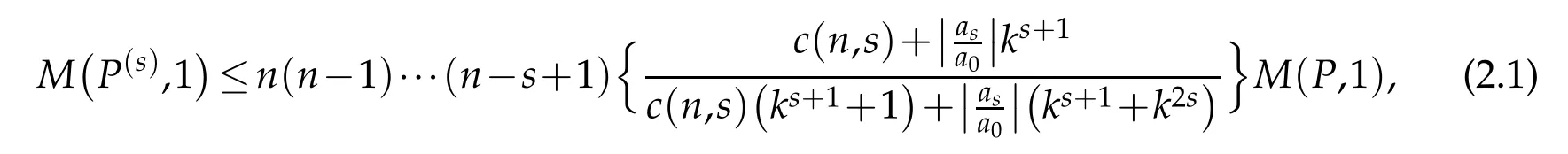
where c(n,j)are the binomial coefficients defined by
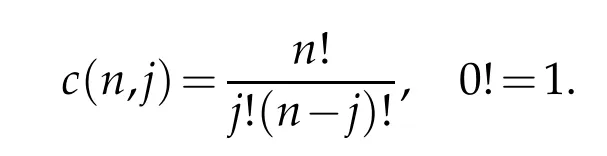
From Lemma 2.1,we easily get
Lemma 2.2.If P∈Pnand P(z)/=0 in|z|<k,k≥1,then for 0≤s<n,we have
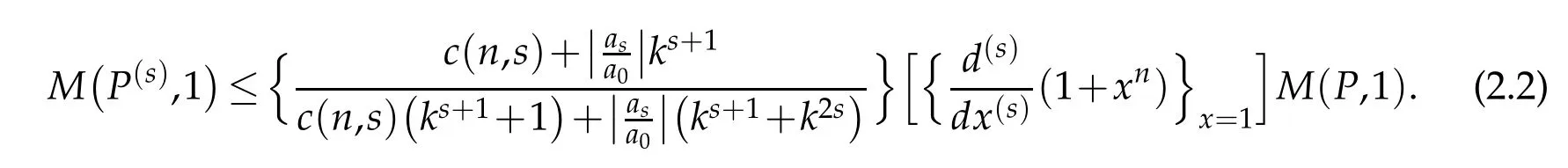
Lemma 2.3.If P∈Pnand P(z)/=0 in|z|<k,k>0,then|P(z)|>m for|z|<k,and in particular
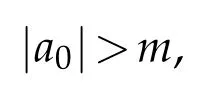
where m=min|z|=k|P(z)|.
The above lemma is due to Gardner,Govil and Musukula[4].
Lemma 2.4.If P∈Pnand P(z)/=0 in|z|<k,k≥1,then for 1≤s<n we have
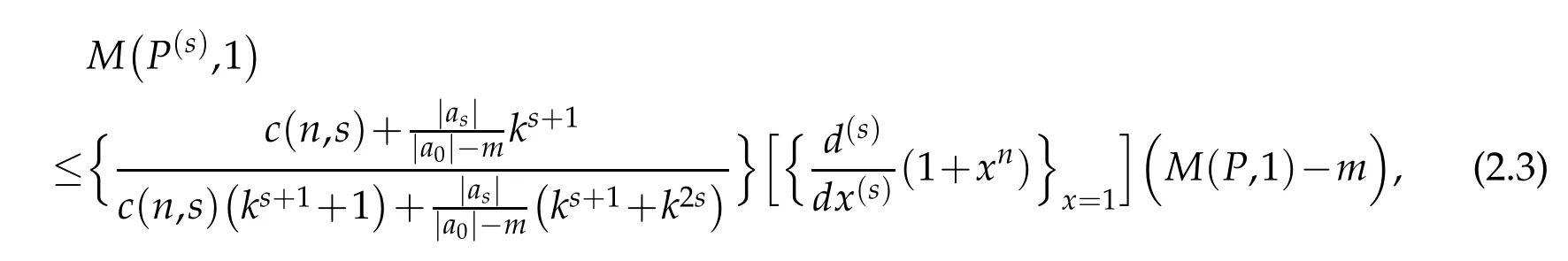
where m=min|z|=k|P(z)|.
The above lemma is due to Mir[7].
Lemma 2.5.If P∈Pnand P(z)/=0 in|z|<k,k>0,then for 0≤s<n,we have

Proof.Since
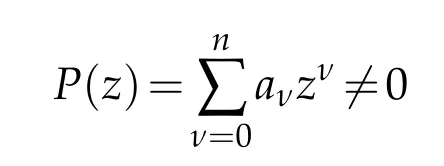
in|z|<k,k>0.Let z1,z2,···,znbe the zeros of P(z),then|zν|≥k;1≤ν≤n,and we have

where ω(n,s)is the sum of all possible products of z1,z2,···,zntaken s at a time.From(2.5c)and(2.5d),we get

which completes the proof of Lemma 2.5.
Lemma 2.6.If
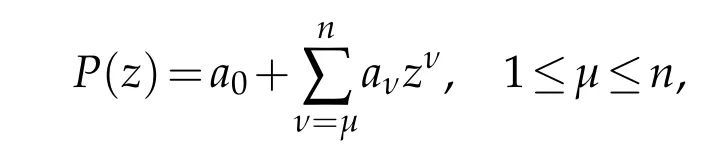
is a polynomial of degree n having no zeros in|z|<k,k>0,then for 0<r≤R≤k,we have
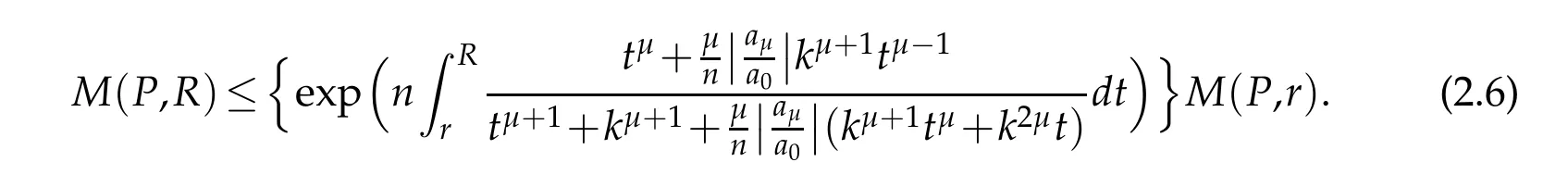
The above result is due to Jain[6].
Lemma 2.7.If
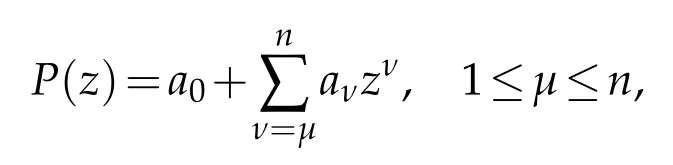
is a polynomial of degree n having no zeros in|z|<k,k>0,then for 0<r≤R≤k,we have
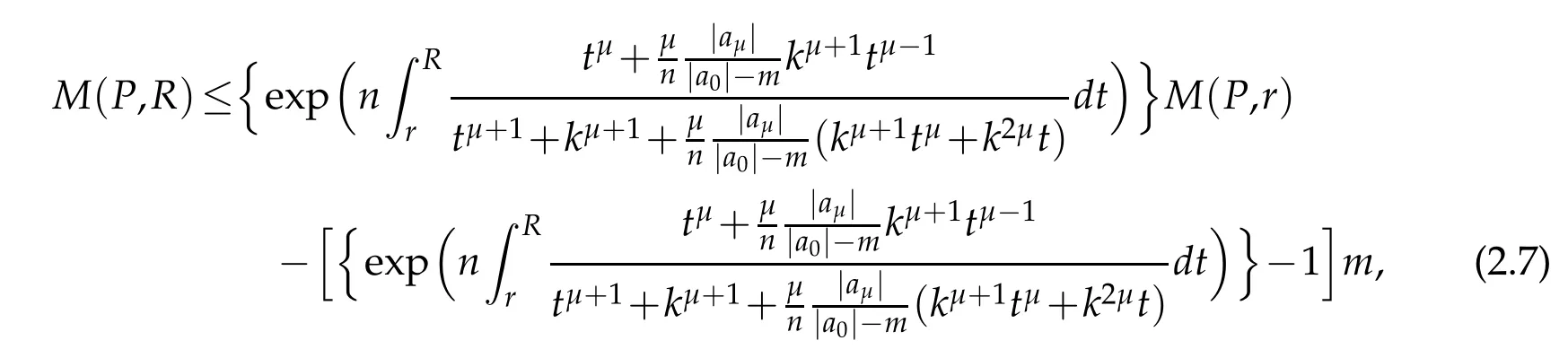
where m=min|z|=k|P(z)|.
The above lemma is due to Chanam and Dewan[3].
3 Proofs of theorems
Proof of Theorem 1.2.Since P(z)/=0 in|z|<k,k>0,the polynomial P(Rz)has no zero in |z|<k/R,k/R≥1.Hence using Lemma 2.2,we have for 0≤s<n,
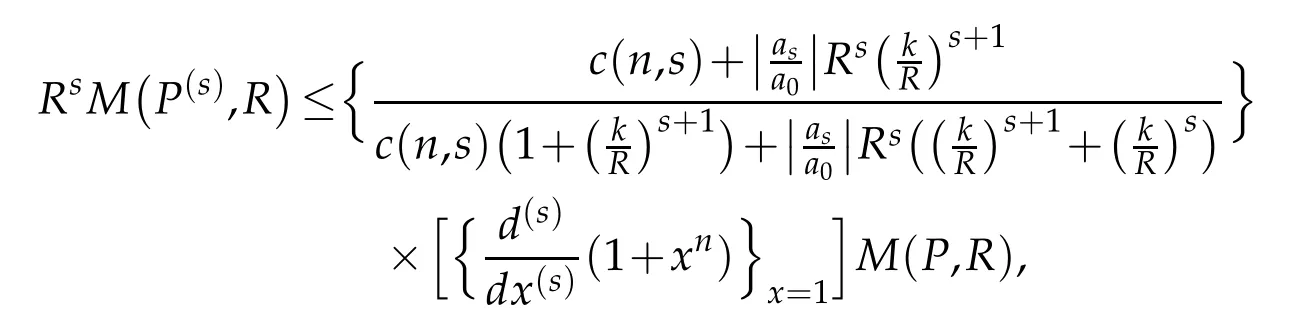
which gives
Now,if 0<r≤R≤k,then by Lemma 2.6,we obtain forµ=1,

Combining(3.1)and(3.2),we obtain
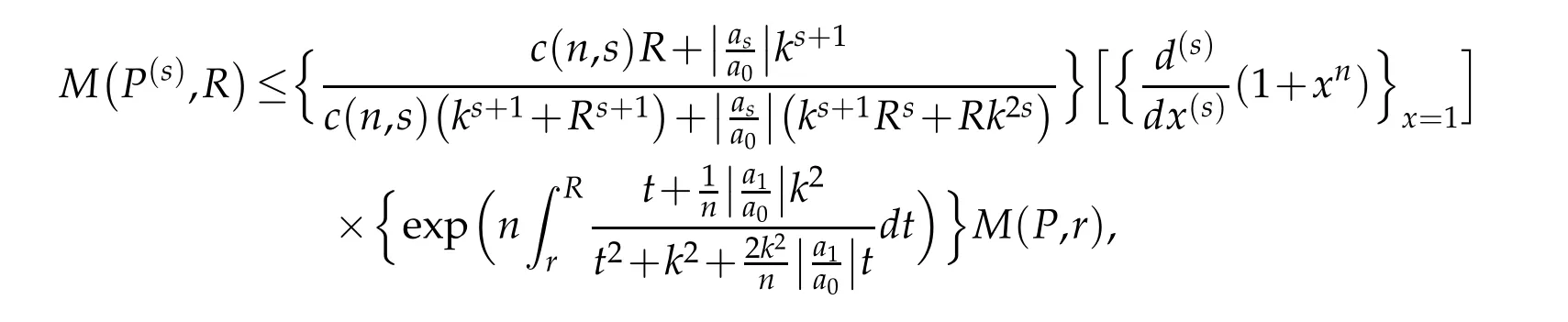
which proves Theorem 1.2.
Proof of Theorem 1.3.Since P(z)has no zero in|z|<k,k>0,the polynomial P(Rz)has no zero in|z|<k/R,k/R≥1.Hence using Lemma 2.4,we have for 1≤s<n,
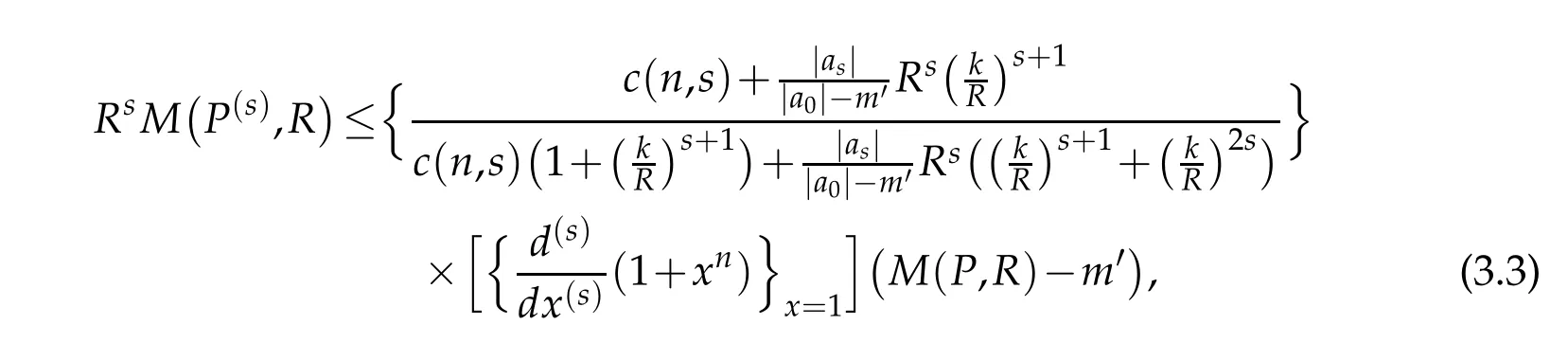
where m′=min|z|=kR|P(Rz)|=min|z|=k|P(z)|=m.This gives
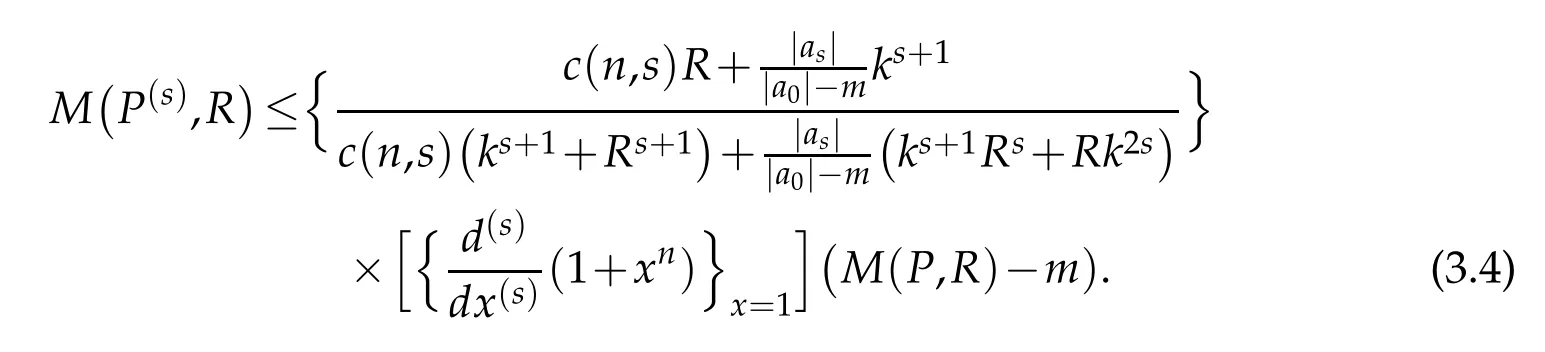
The above inequality when combined with Lemma 2.7(forµ=1)gives inequality(1.12)and this completes the proof of Theorem 1.3.
[1]N.C.Ankeny andT.J.Rivlin,On a theoremofS.Bernstein,PacificJ.Math.,5(1955),849-852.
[2]A.Aziz and N.A.Rather,Some Zygmund type Lqinequalities for polynomials,J.Math. Anal.Appl.,289(2004),14-29.
[3]B.Chanam and K.K.Dewan,Inequalities for a polynomial and its derivative,J.Math.Anal. Appl.,336(2007),171-179.
[4]R.B.Gardner,N.K.Govil and S.R.Musukula,Rate of growth of polynomials not vanishing inside a circle,J.Ineq.Pure Appl.Math.,6(2)(2005),1-9.
[5]V.K.Jain,A generalization of Ankeny and Rivlin's result on the maximum modulus of polynomials not vanishing in the interior of the unit circle,Turk.J.Math.,31(2007),89-94.
[6]V.K.Jain,On maximum modulus of polynomials with zeros outside a circle,Glasnik Mate.,29(1994),267-274.
[7]A.Mir,Inequalities for the growth and derivatives of a polynomial,African Diaspora J. Math.,18(2015),18-25.
[8]Q.I.Rahman and G.Shmeisser,Analytic Theory of Polynomials,Oxford University Press,New York,2002.
[9]A.C.Schaeffer,Inequalities of A.Markoffand S.Bernstein for polynomials and relatedfunctions,Bull.Amer.Math.Soc.,47(1941),565-579.

.Email address:mabdullah mir@yahoo.co.in(A.Mir)
14 November 2015;Accepted(in revised version)6 May 2016
杂志排行
Analysis in Theory and Applications的其它文章
- Multilinear Fractional Integrals and Commutators on Generalized Herz Spaces
- Characterizations of Null Holomorphic Sectional Curvature of GCR-Lightlike Submanifolds of Indefinite Nearly K¨ahler Manifolds
- Commutators of Lipschitz Functions and Singular IntegralswithNon-Smooth KernelsonEuclideanSpaces
- Commutators ofLittlewood-PaleyOperatorsonHerz Spaces with Variable Exponent
- A Characterization of MRA Based Wavelet Frames Generated by the Walsh Polynomials
- Box Dimension of Weyl Fractional Integral of Continuous Functions with Bounded Variation
