基于LWE的单层同态云计算方案

王旭阳　 胡爱群　 方　昊

(东南大学信息科学与工程学院, 南京 210096)



基于LWE的单层同态云计算方案

王旭阳 胡爱群 方昊

(东南大学信息科学与工程学院, 南京 210096)

为了实现安全的远程操作,通过分析研究一次或单层的同态运算,构造了一个基于错误学习(LWE)的单层同态云计算方案(sLHCC).首先,根据解密者是否知道LWE问题中所使用的随机向量,构造了2个不同的单层同态加密方案sLHE1和sLHE2,并得到了相应的sLHCC方案.该方案在保持LWE问题困难性的基础上,实现了云端单次的同态加和乘运算.根据合理的操作约定和同态结果,用户可以在不泄露操作需求(密文)的情况下,执行远程操作和控制.结果表明,与其他同态加密方案相比,sLHCC的公钥尺寸从传统的矩阵降为向量,从而减小了密文尺寸和云端的存储需求.

云计算;格密码;错误学习;同态;远程操作

随着智能终端的快速发展,远程操作和控制已经被越来越多的用户所接受.用户将远端的操作和控制对象以及相应的操控按照特定方式命名,便可通过云端实现对操作和控制对象的操控.然而,在实际应用中用户操作和信息传输的安全性却没有得到足够的保障[1].随着计算能力的日益强大,攻击者对于密码系统的攻击能力也不断提升.为了提高安全性,人们不得不提高安全参数的长度,并对传统密码学模型进行改进.然而,量子计算机强大的并行计算能力,使其具有解决传统密码学模型中困难问题的能力.

作为格密码的载体,格的研究虽然有着长达200多年的历史,但成为密码学上的研究热点却仅在近来这二十多年.与传统密码学模型不同,格困难问题可以归约为一般问题,在这一特性下,攻击基于具体格问题构造的密码系统等同于求解相应的格困难问题.1997年Ajtai[2]率先给出了上述特性的一个肯定性归约结果.文献[3-4]获得了一系列与格困难问题归约有关的结果,为构造满足相应安全需求的格密码系统提供了理论支持.

本文基于LWE问题构造了单层同态云方案sLHCC.该方案在保持LWE问题困难性的基础上,实现了云端单次的同态加和乘运算.根据合理的操作约定和同态结果,用户可以在不泄露操作需求(密文)的情况下,执行远程操作和控制.

1　基本概念

对于任意实数r,⎣r⎤=⎣r+1/2⎤表示距离r最近的整数.对于任意正整数θ,poly(θ)表示非特指的多项式函数,negl(θ)表示非特指的θ阶可忽略函数.

1.1格

1.2高斯分布

对于任意正实数s>0,数学期望为c∈Rn、标准差为s的高斯分布定义如下:

∀y∈Rnρs,c(y)=e-π‖y-c‖2/s2

当s=1,c=0时,可将ρs,c(y)的下标省去,用ρ(y)代替.简单起见,下文中假设所有算法都能有效地按照高斯分布抽样.

对于任一格空间L,离散高斯分布定义如下:

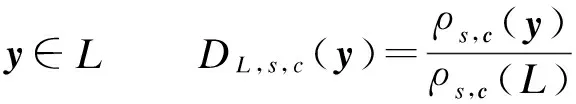
1.3LWE困难问题

定义1(误差学习(LWE))给定Zq上一概率分布χ和Ax,χ上任意多个抽样,求解x.

1.4同态

公钥体制的加密方案ε通常由密钥生成算法KeyGen、加密算法Encrypt、评估算法Evaluate和解密算法Decrypt四个算法组成[5-10].密钥生成算法和加解密算法与传统加密方案类似.评估算法中,通过输入公钥pk、密文组(c1,c2,…,ct)和某一电路C,得到一个新的密文c,其中t≥2为同态运算涉及的明文数量.

定义3(同态算法的正确性)给定密钥生成算法KeyGen,支持t个以上输入的电路C和t明文(m1,m2,…,mt),如果对于任意生成的密钥对(pk,sk)和通过ci=Encrypt(pk,mi)加密得到的密文组(c1,c2,…,ct),等式Decrypt(sk,Evaluate(pk,C,(c1,c2,…,ct)))=C(m1,m2,…,mt)成立,则称同态公钥加密方案ε=(KeyGen,Encrypt,Evaluate,Decrypt)正确.

2　单层同态加密方案

目前,研究者们已构造出大量的同态乃至全同态加密方案[5-10].在构造同态方案的过程中,通常遵循2个研究方向:① 强化方案的自我修正能力,加强方案在同态运算层数方面的能力直至实现真正的全同态运算;但这会导致方案复杂化,公共参数、公私钥和密文等数量都可能急剧增大[5,7-10].② 在保证足够安全性和同态运算层数的情况下,尽量减小各种参数数量,从而使得方案简单化[6-7].

2) sLHE1.Encrypt(pk,sk,m1,m2,…,mt):给定加密信息mi∈GF(p1),根据分布χ随机选择高斯参量ei∈Zq,输出密文ci=mi+aix+ei(modq)和相应的同态计算需求.

3) sLHE1.Evaluate(c1,c2,…,ct):通过同态加 (可以一次多个密文) 和同态乘(一次2个密文),计算并输出同态加结果cA和同态乘结果cM.

4) sLHE1.Decrypt(sk,cA,cM):根据不同评估情况进行解密.

显然,sLHE1方案实现了单次的同态加和同态乘运算.由于加密方和解密方为同一用户,加、解密方拥有了方案使用过程中的所有随机数,从而使得sLHE1方案拥有比其他格密码方案更高的解密成功率.

结论1当mi∈GF(p1)时,sLHE1方案的密文可以被正确解密.

证明为简单起见,假定仅有2个密文参与同态加和同态乘运算(即t=2),则

(cA-(a1+a2)x)-e1-e2)(modq)=

(m1+m2)(modq)

(cM+a1xa2x-a1c2x-a2c1x-e1m2-e2m1-e1e2)(modq)=

(m1m2)(modq)

事实上,当同态加密文数不大于t时,仍有(m1+m2)≤q-1,则

(cA-(a1+a2+…+at)x)-e1-e2-…-et)(modq)=

(m1+m2+…+mt)(modq)

式中,cA=c1+c2+…+ct.证毕.

值得注意的是,sLHE1方案并不是一个标准的加密方案.sLHE1加密和解密都是由同一用户进行的,故公、私钥可以互换或者同时作为加密密钥.用户可以通过预处理来简化运算过程中的计算复杂度.

由于解密方知道加密方加密时所使用的高斯随机向量,因此在解密过程中不会因为相应的随机向量产生误差.但在实际应用中,解密方难以同时获得这些信息.为了解决这一问题,给定公共参数p2=p1/2,将sLHE1方案改进为单层同态加密方案sLHE2.sLHE2方案由以下4个算法组成.

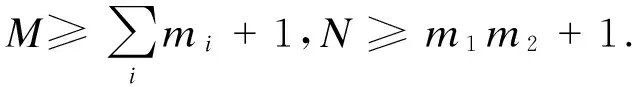
3) sLHE2.Evaluate(c1,c2,…,ct,M,N):通过同态加 (可以一次多个密文) 和同态乘(一次2个密文),计算并输出同态加结果cA和同态乘结果cM.

4) sLHE2.Decrypt(sk,cA,cM):根据不同评估情况进行解密.

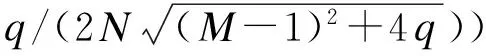
证明证明方法与结论1类似.需要注意的是,解密时需要成功消去高斯随机向量带来的密文噪音,即M(e1+e2+…+et)≤q/2和N(e1m2+e2m1+Ne1e2)≤q/2.

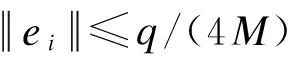
M(e1+e2+…+et)≤q/2

2N(e1m2+e2m1+Ne1e2)≤

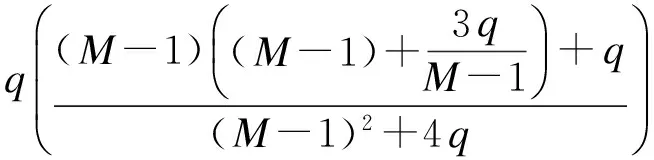
证毕.

3　单层同态云计算方案

远程操作和控制问题描述如图1所示.首先,用户将远程操作和控制对象按照特定方式命名得到明文,并通过不同的运算定义不同操控.加密方将得到的明文和运算需求发送到云端.云端通过同态运算将相应结果发送给解密方,解密方解密后便可通过运算结果实现对操作对象的操控.

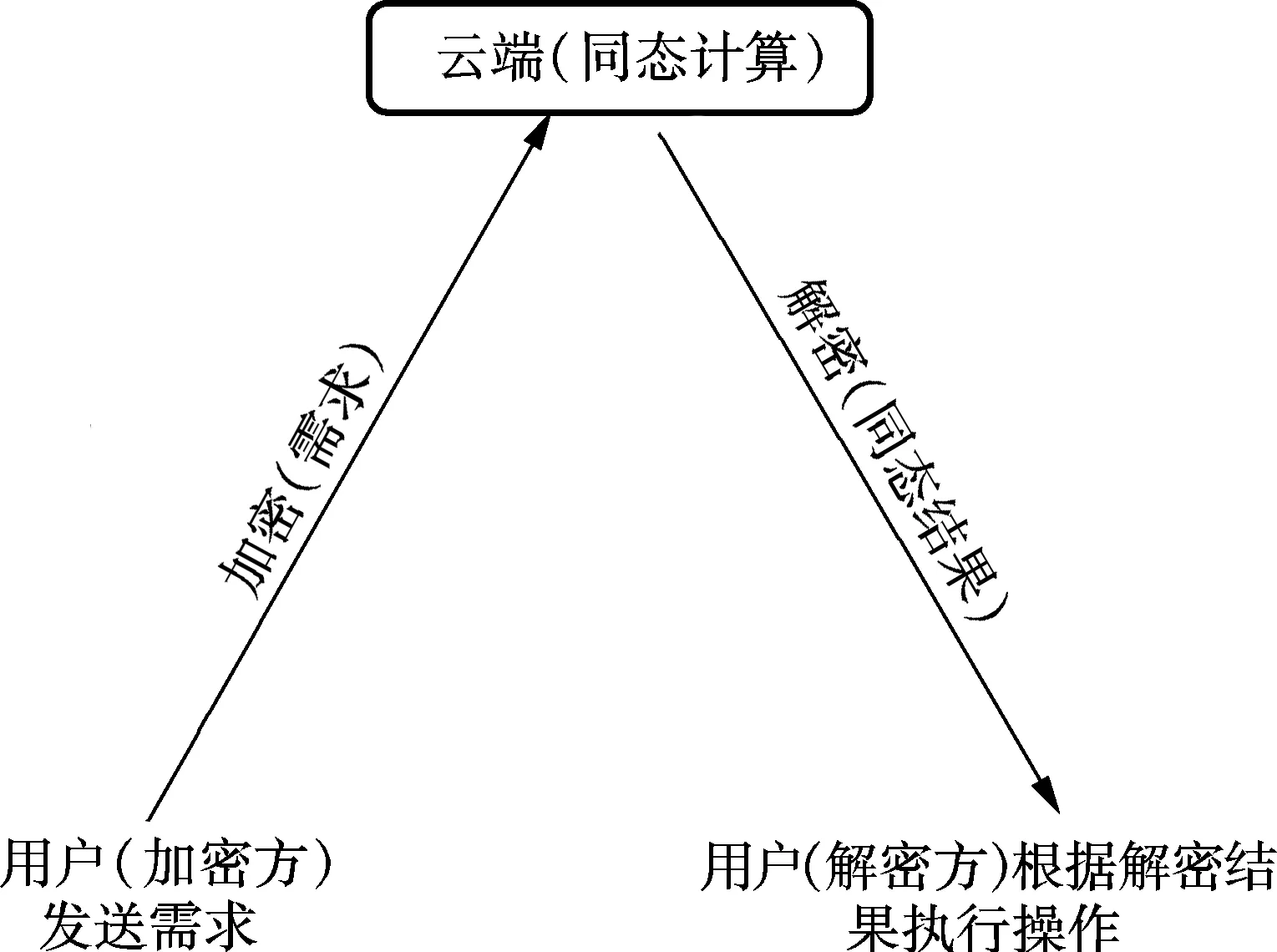
图1　远程操作和控制问题描述

给定公共参数p={p1(sLHE1),p2(sLHE2)},并用op={+,·}表示同态运算集合,根据方案sLHE1或sLHE2构造出安全单层同态云计算方案(sLHCC).需要注意的是,选定了sLHE方案后,整个sLHCC方案须依据同一sLHE方案构造.sLHCC方案由以下4个算法组成.

1) sLHCC.KeyGen(1n):用户通过sLHE1.KeyGen或sLHE2.KeyGen得到相应的公私钥(pk,sk).

2) sLHCC.Encrypt(sk,pk,m):用户根据云同态计算明文信息m∈GF(p)确定参数t,q和p.通过sLHE1.Encrypt或sLHE2.Encrypt,按同态计算顺序输出密文(c1,c2,…,ct,ο),其中ο∈op表示某种同态运算.

3) sLHCC.Evaluate(c1,c2,…,ct,ο):根据用户需求,服务器端通过sLHE1.Evaluate或sLHE2.Evaluate计算同态加 (可以一次多个密文) 或者同态乘(一次2个密文),并输出结果cA和cM.

4) sLHCC.Decrypt(sk,cA,cM):用户根据不同同态情况通过sLHE1.Decrypt或sLHE2.Decrypt进行解密.

结论3当m∈GF(p)时,sLHCC方案的密文可以被正确解密.

容易发现sLHCC方案的公、私钥是相互独立抽取的,因此即使用户重复使用同一私钥,云端也难以得到相应的私钥.事实上,云端破解方案获取私钥的困难等同于求解相应的LWE困难问题.根据文献[2,5,11-15]中关于格困难问题和一般问题相互归约的结论可知,LWE问题在给定参数下的复杂度为NP∩coNP[2,14-15].这意味着在多项式时间内求解相应的LWE问题是不可能的,攻击者也不可能在多项式时间内破解相应的方案.

为了讨论sLHCC方案的安全性,下面给出不可区分选择明文安全(IND-CPA)的定义[5].

结论4单层同态云计算方案sLHCC是IND-CPA的.

证明由引理1可知,sLHE1.Encrypt和sLHE2.Encrypt加密得到的密文与Zq上的随机均匀抽样是计算不可区分的.在信息传输过程中没有泄露任何与密文有关的信息,因此,云端得到的密文仍与Zq上的随机均匀抽样是计算不可区分的.对于均匀抽样,易知pr[φ(pk,Evaluate,Encryptpk(0))=1≈pr[φ(pk,Evaluate,Encryptpk(1))=1,即任意多项式敌手φ获得的优势AdvCPA(φ)=negl(n),因此sLHCC是IND-CPA的.

4　复杂度分析

执行一轮sLHCC方案所需的计算复杂度见表1.与常见的同态方案[5-7]只能支持GF(2)计算不同,sLHCC方案支持更大范围(GF(p))内数据的计算.由于一次减操作所需的计算量与一次加操作相同,故此处将其视为同一操作.

表1　单轮sLHCC方案的复杂度分析

在sLHCC方案中,将加、解密两方视为同一用户,拥有共同的私钥,因此当解密者知道进行加密操作的高斯向量值时,解密者可以通过直接计算成功解密,而不用担心其他格密码体制中由于随机参数导致的解密成功率问题.由此可知,本方案不需要通过多次运行来增加解密成功率.故而采用本方案可以减少相应的参数尺寸.表2给出了本方案与一般LWE加密方案时的参数尺寸比较.由表可知,与LWE加密方案相比,虽然sLHCC的私钥尺寸没有明显变化,但是公钥尺寸从传统的矩阵降为向量,从而减小了密文尺寸和云端的存储需求.同时,执行一次sLHCC方案所能加密的明文数量大于普通LWE加密方案.因此,在对非单个明文进行加密运算时,sLHCC方案较一般LWE加密方案拥有更高效的执行效率.

表2　参数尺寸比较

5　结语

本文以格困难问题LWE为基础,构造了一个单层同态云计算方案sLHCC.与基于传统密码学方案相比,sLHCC在理论上拥有更好的安全性和抗攻击能力.在实际应用中,除去密文使用到了私钥外,公、私钥之间互信息为零,这使得用户不需要频繁更新用户私钥.此外,该方案每次只需执行单层同态运算,相比一般LWE加密方案,sLHCC拥有更小的参数尺寸.这些优势增加了方案的效率,减小了云端存储的空间占用,为构造安全可存储的单层同态云计算方案提供了基础.

References)

[1]Aguilar-Melchor C, Fau S, Fontaine C, et al. Recent advances in homomorphic encryption: A possible future for signal processing in the encrypted domain[J].IEEESignalProcessMag, 2013, 30(2): 108-117. DOI:10.1109/msp.2012.2230219.

[2]Ajtai M. Generating hard instances of lattice problems[C]//ProceedingsoftheTwenty-EighthAnnualACMSymposiumonTheoryofComputing. New York: ACM, 1996: 99-108. DOI:10.1145/237814.237838.

[3]Wang X Y, Hu A Q. Complexity analysis of lattice hard problems[J].JournalofCryptologicResearch, 2015, 2(1): 1-16.

[4]Micciancio D, Regev O. Lattice-based cryptography[M]//Post-quantumcryptography. Berlin: Springer, 2009: 147-191. DOI:10.1007/978-3-540-88702-7_5.

[5]Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[J].SIAMJournalonComputing, 2014, 43(2): 831-871.

[6]Boneh D, Gentry C, Halevi S, et al. Private database queries using somewhat homomorphic encryption[M]//AppliedCryptographyandNetworkSecurity. Berlin: Springer, 2013: 102-118. DOI:10.1007/978-3-642-38980-1_7.

[7]Van Dijk M, Gentry C, Halevi S, et al. Fully homomorphic encryption over the integers[C]//Advancesincryptology—EUROCRYPT2010. Berlin: Springer, 2010: 24-43.

[8]Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[C]//Proceedingsofthe3rdInnovationsinTheoreticalComputerScienceConference. New York: ACM, 2012: 309-325.

[9]Brakerski Z. Fully homomorphic encryption without modulus switching from classical GapSVP[C]//AdvancesinCryptology—CRYPTO2012. Berlin: Springer, 2012: 868-886. DOI:10.1007/978-3-642-32009-5_50.

[10]Gentry C, Sahai A, Waters B.Homomorphic encryption from learning with errors: Conceptually-simpler,asymptotically-faster,attribute-based[C]//AdvancesinCryptology—CRYPTO2013. Berlin: Springer, 2013: 75-92. DOI:10.1007/978-3-642-40041-4_5.

[11]Micciancio D, Peikert C. Hardness of SIS and LWE with small parameters[C]//AdvancesinCryptology—CRYPTO2013. Berlin: Springer, 2013: 21-39. DOI:10.1007/978-3-642-40041-4-2.

[12]Brakerski Z, Langlois A, Peikert C, et al. Classical hardness of learning with errors[C]//Proceedingsofthe45thAnnualACMSymposiumonTheoryofComputing. New York: ACM, 2013: 575-584. DOI:10.1145/2488608.2488680.

[13]Aharonov D, Regev O. Lattice problems in NP ∩ coNP[J].JournaloftheACM, 2005, 52(5): 749-765. DOI:10.1145/1089023.1089025.

[14]Peikert C. Limits on the hardness of lattice problems in lpnorms[J].ComputationalComplexity, 2008, 17(2): 300-351. DOI:10.1007/s00037-008-0251-3.

[15]Regev O. The learning with errors problem[C]//ProceedingsofIEEEConferenceonComputationalComplexity. Berlin: Springer, 2010: 191-204.

Single-layer homographic cloud computing scheme based on LWE

Wang Xuyang Hu Aiqun Fang Hao

(School of Information Science and Engineering, Southeast University, Nanjing 210096, China)

To achieve safe remote operation, a single-layer homographic cloud computing scheme(sLHCC) based on learning with errors(LWE) is constructed by analyzing one-time-layer or single-layer homomorphic operation. First, according to whether the decryption accesses the random vector in LWE problem or not, two different single-layer homographic encryption schemes, named sLHE1 and sLHE2, are proposed, and the corresponding sLHCC schemes are put forward. The sLHCC schemes can realize one-time homomorphic addition and one-time homomorphic multiplication in cloud with maintaining the difficulty of LWE problem. According to the reasonable operation agreement and homomorphism results, users can execute the remote operation and control without leaking operation requirements (ciphertexts). The results show that compared with other homomorphic encryption schemes, the size of the public key of the sLHCC schemes reduces from matrix to vector, inducing the decrease of the ciphertext size and the demands of the cloud storage.

cloud computing; lattice-based cryptography; learning with errors(LWE); homographic; remote operation

10.3969/j.issn.1001-0505.2016.05.008

2016-01-21.作者简介: 王旭阳(1985—),男,博士生;胡爱群(联系人),男,博士,教授,博士生导师,aqhu@seu.edu.cn.

国家重点基础研究发展计划(973计划)资助项目(2013CB338003).

TP309.7

A

1001-0505(2016)05-0945-05

引用本文: 王旭阳,胡爱群,方昊.基于LWE的单层同态云计算方案[J].东南大学学报(自然科学版),2016,46(5):945-949. DOI:10.3969/j.issn.1001-0505.2016.05.008.