基于字典学习的超分辨率显微CT图像重建

姚佳丽　 李中源　 吴华珍　 李　光　 罗守华

(东南大学生物科学与医学工程学院, 南京 210096)



基于字典学习的超分辨率显微CT图像重建

姚佳丽 李中源 吴华珍 李光 罗守华

(东南大学生物科学与医学工程学院, 南京 210096)

为提高显微CT重建图像的空间分辨率,提出了一种基于字典学习的超分辨率图像重建算法．首先,将重建图像进行网格细化,并使用面积权值模型实现对投影过程的精确建模．然后,选择高质量的图像作为训练样本,采用K-SVD算法构建图像字典．基于该图像字典,利用正交匹配追踪算法实现对重建图像的稀疏表达,并以此作为稀疏项约束引入到重建算法的目标函数中．最后,使用梯度下降法求解目标函数．实验结果表明:与传统的基于插值的超分辨率重建算法相比,所提算法的超分辨率结果在图像对比度、边缘保持方面具有优势,并且保留了更多的图像高频信息,从而有效提高了重建图像的空间分辨率．

超分辨率重建;字典学习;面积权值;微计算机断层扫描技术

微计算机断层扫描技术(又称显微CT)是一种非破坏性、非介入式、高分辨率的成像技术,能够在不破坏样本的情况下了解样本的内部显微结构,从而被广泛应用于医学、药学、材料学、工业无损探测等领域．在保证X射线安全剂量的前提下,重建图像的空间分辨率是各种应用中所关注的最重要的指标之一,它的提高对于显微CT在各领域中的进一步应用具有显著意义[1]．然而,在实际成像过程中,重建图像空间分辨率的提高往往受限于设备的物理条件和实际应用要求,如X射线辐射剂量、扫描时间、探测器配置以及扫描的几何结构等．因此,提高显微CT成像的空间分辨率成为研究的热点和难点．

目前的解决方案可分为以下3类[2]:① 通过缩短探测器孔隙宽度及探测器单元间距,提高探测器的分辨率;但该方案会受到物理硬件条件的限制[3],若探测器单元大小超过衍射极限,还需要考虑衍射造成的影响．② 通过局部成像,将感兴趣区域放大,以提高投影的空间分辨率[3];但该方案会导致投影数据横向截断,理论上不能实现精确重建,重建图像往往存在杯状伪影,从而导致图像质量下降．③ 改变扫描方式以提高采样频率,具体实现方式包括探测器中心偏置1/4像素扫描技术[4]、射线源焦点摆动法[5]及像素错位技术[6]等;但该方案对机械精度要求较高,并且多次曝光会使X射线的辐射剂量加倍．

近年来,压缩感知理论在图像放大、去噪及恢复等领域得到越来越多的关注,在该理论基础上建立的基于学习的超分辨率重建算法成为相关研究的热点．Freeman等[7]提出了基于样本图像学习的超分辨率重建算法,充分利用自然图像集,实现了基于学习的超分辨率重建算法的扩展和开发; Wang等[8]提出了一种基于实例的超分辨率重建算法,通过对图像块之间稀疏性关联的学习，重建了高分辨率图像;Jeong等[9]利用K均值算法学习构建了分类字典,并利用分类字典实现了单幅图像的重建．上述算法通过对高、低分辨率训练样本的学习,建立了一种高低分辨率的对应关系,相比于传统的基于插值的超分辨率重建算法[10]可获得更多的细节信息．然而,目前关于这类算法的研究主要集中于自然图像．本文将字典学习的方法应用到CT超分辨率图像重建中．通过将重建图像网格细化和使用精度更高的系数矩阵,采用字典学习的方法对重建图像进行稀疏表达,并作为重建算法的稀疏项约束,利用直接获得的投影数据进行超分辨率图像重建．

1　超分辨重建模型的建立

图像离散化后,CT图像重建可以转化为如下的代数方程:

(1)

式中,vj为重建图像V的像素值,其中,j=1,2,…,N,N=Nwid×Nhei为重建图像的像素点总数,Nwid,Nhei分别为重建图像的宽度和高度,即V∈RNwid×Nhei;投影数据矩阵P的元素pi表示第i条投影射线的投影值,其中,i=1,2,…,M,M=Mproj×Mbin为投影射线总数,Mproj,Mbin分别为投影的角度数和探测器的宽度,即P∈RMproj×Mbin;系数矩阵W的元素wij为投影系数,表示第j个像素对第i个投影值的贡献．式(1)可写成矩阵相乘的形式,即

WV=P

(2)

传统采样过程中,将重建图像V离散化为Nwid×Nhei的离散图像(见图1(a)),每个像素的大小与探测器像元的大小相同．王丽艳等[11]从采样定律和压缩感知理论出发,利用稀疏表示的先验知识,证明可通过原有的低数据量测量进行高精度图像重建．由此提出了一种超分辨重建模型,将重建图像V进一步细分为ηNwid×ηNhei,其中η∈Z为超分辨因子,且η>1．超分辨因子为2时重建图像的超分辨率网格的示意图见图1(b),重新离散化后像素的大小为探测器像元大小的1/η．

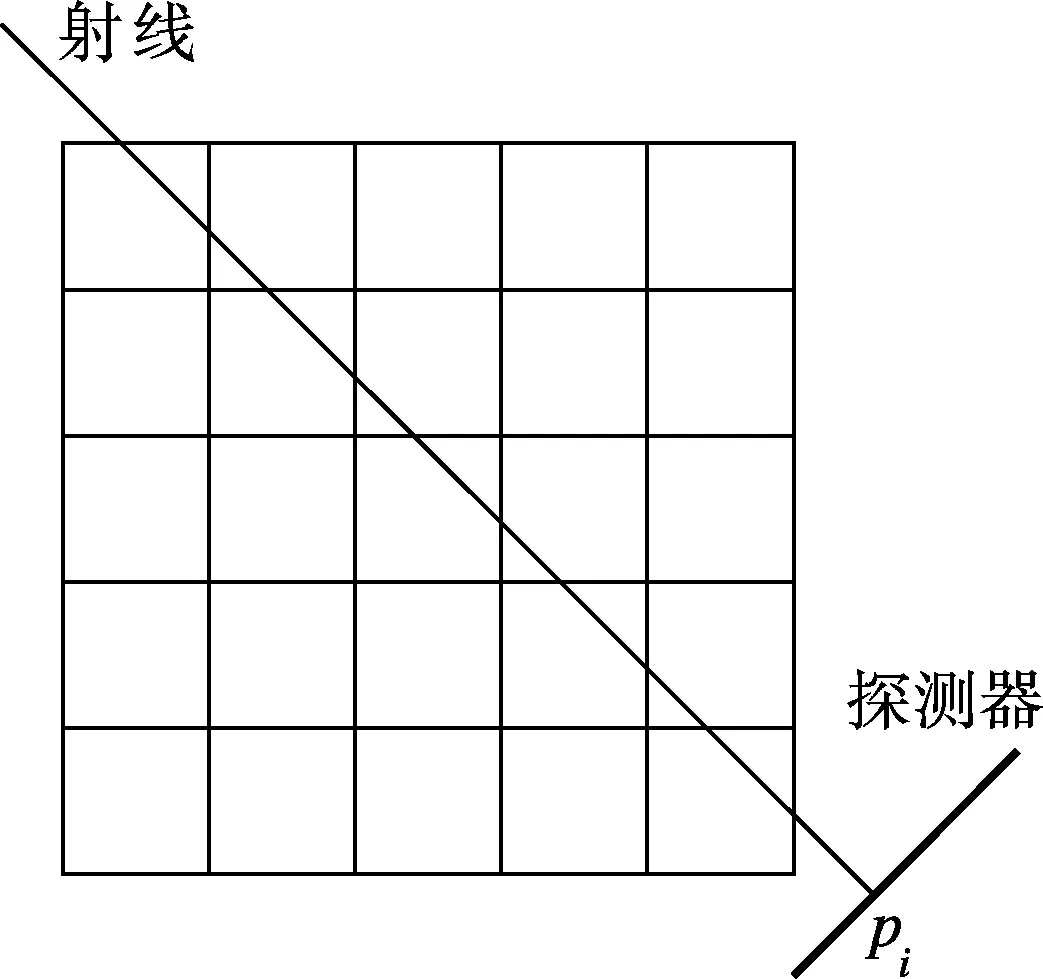
(a) 重建图像网格

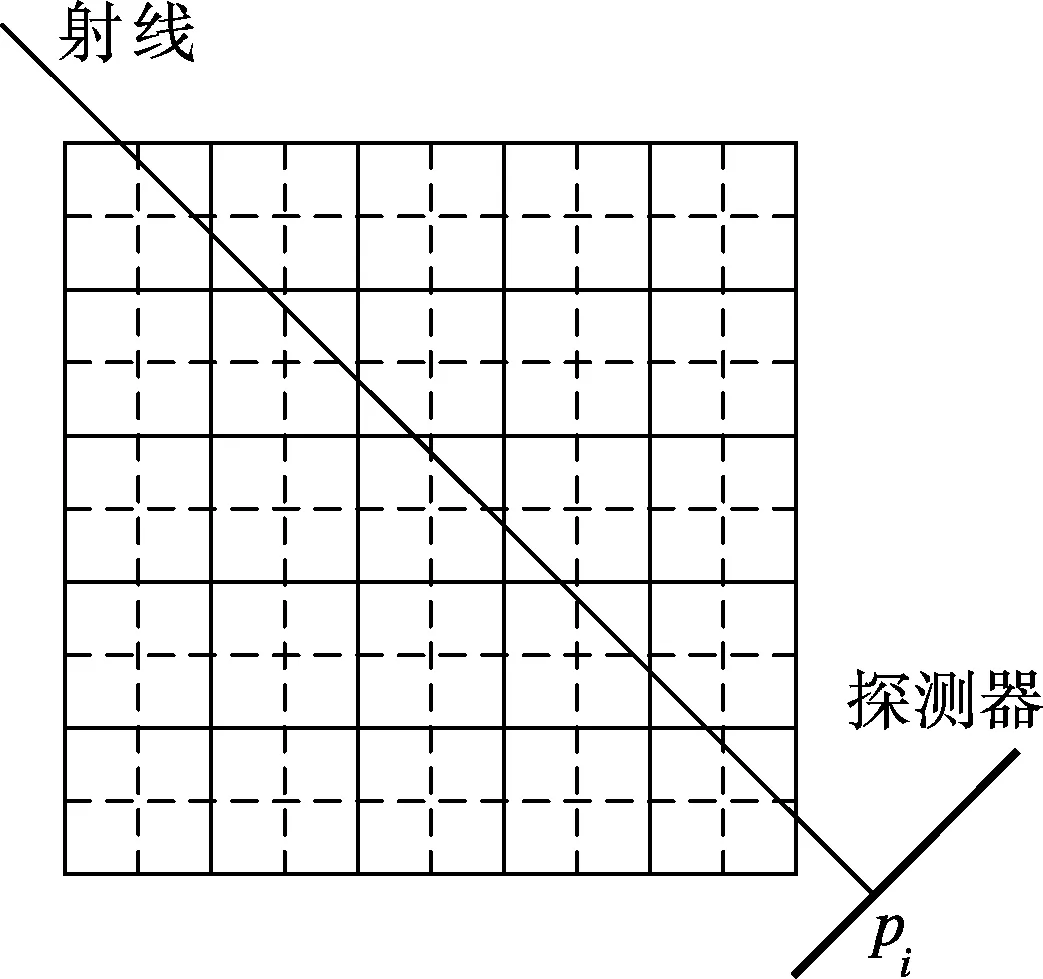
(b) 重建图像的超分辨率网格

根据提出的重建模型,CT图像重建转化为新的代数方程:

AX=P

(3)

式中,X∈RηNwid×ηNhei为图像V经过超分辨率网格细化后的重建图像;A为图像V经过超分辨率网格细化后的系数矩阵,其元素aij为投影系数．在压缩感知理论下,假设重建图像X经过某种变换φ作用后稀疏化,利用原有的投影数据P,可以重建出空间分辨率提高了η2的图像．重建过程为求解稀疏优化的问题,即

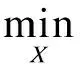
s.t.AX=P

(4)

超分辨重建的目的在于尽可能保持图像的高频信息,即需要对投影过程进行精确建模并对系数矩阵精确求解,因此aij的获取是重建算法中的关键．常用方法为长度权值法(见图2(a)),即将射线看作没有宽度的直线,将其与图像像素相交的长度作为该像素对射线贡献的权值(即图2(a)中箭头标注的线段长度);该方法简单易行,但精度较低,难以满足本文算法的要求．为此,本文采用如图2(b)所示的面积权值法来确定权重,即将射线视作具有宽度的射束,将其与像素方块重叠的面积作为贡献的权值(即图中阴影区域的面积)．与长度权值法相比,面积权值法虽然计算复杂,但更符合工程实际,重建图像质量更优．

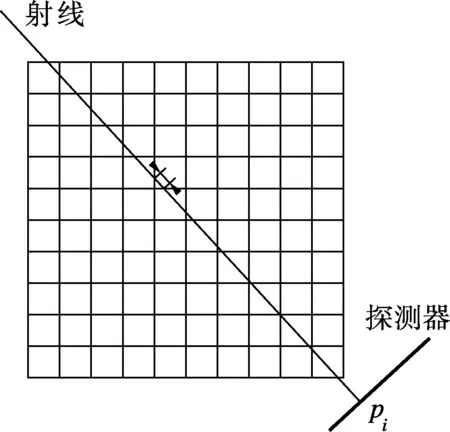
(a) 长度权值法

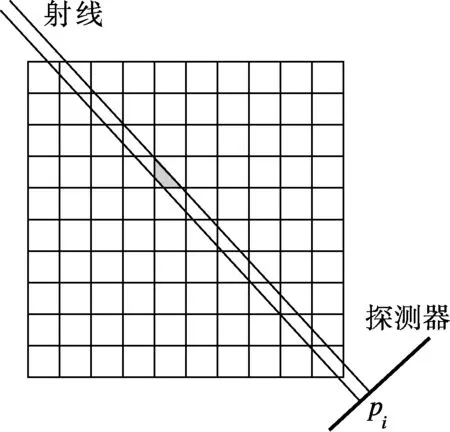
(b) 面积权值法

以等角扇束扫描方式为例,在二维平面上,当射线源旋转至某一投影角度时,计算相邻2条投影射线在像素边界的交点坐标,以及被穿过的像素在整个重建图像中的索引号,并将其保存到数组中;然后,从第1个交点坐标开始,根据相邻射线在像素边界的交点情况,确定射线束与像素格相交的多边形形状．图3(a)为射线束穿过重建区域的示意图．图中,tim表示第i条投影射线与像素网格的交点,m=1,2,…,10为交点的索引号．

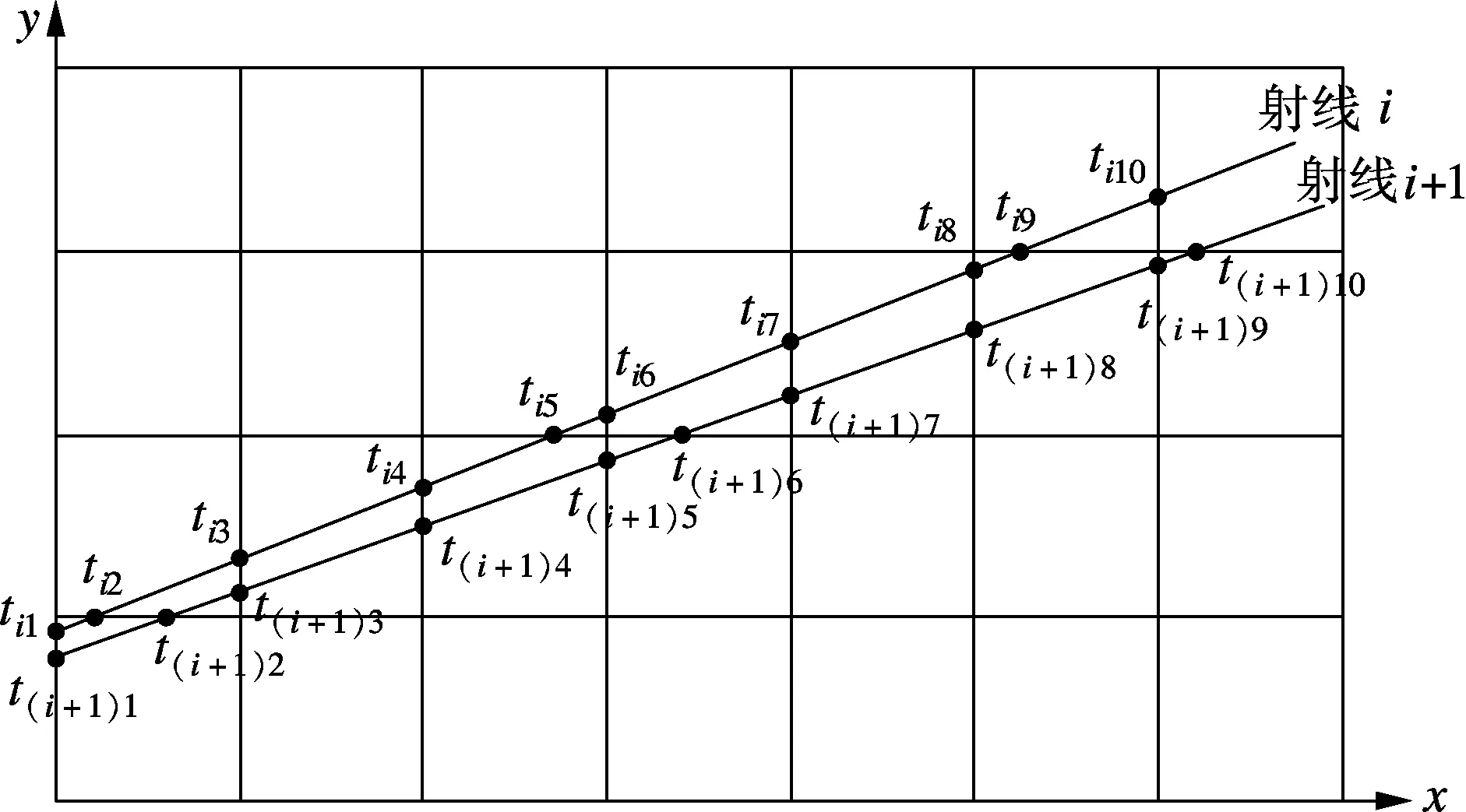
(a) 射线束穿过重建区域的示意图

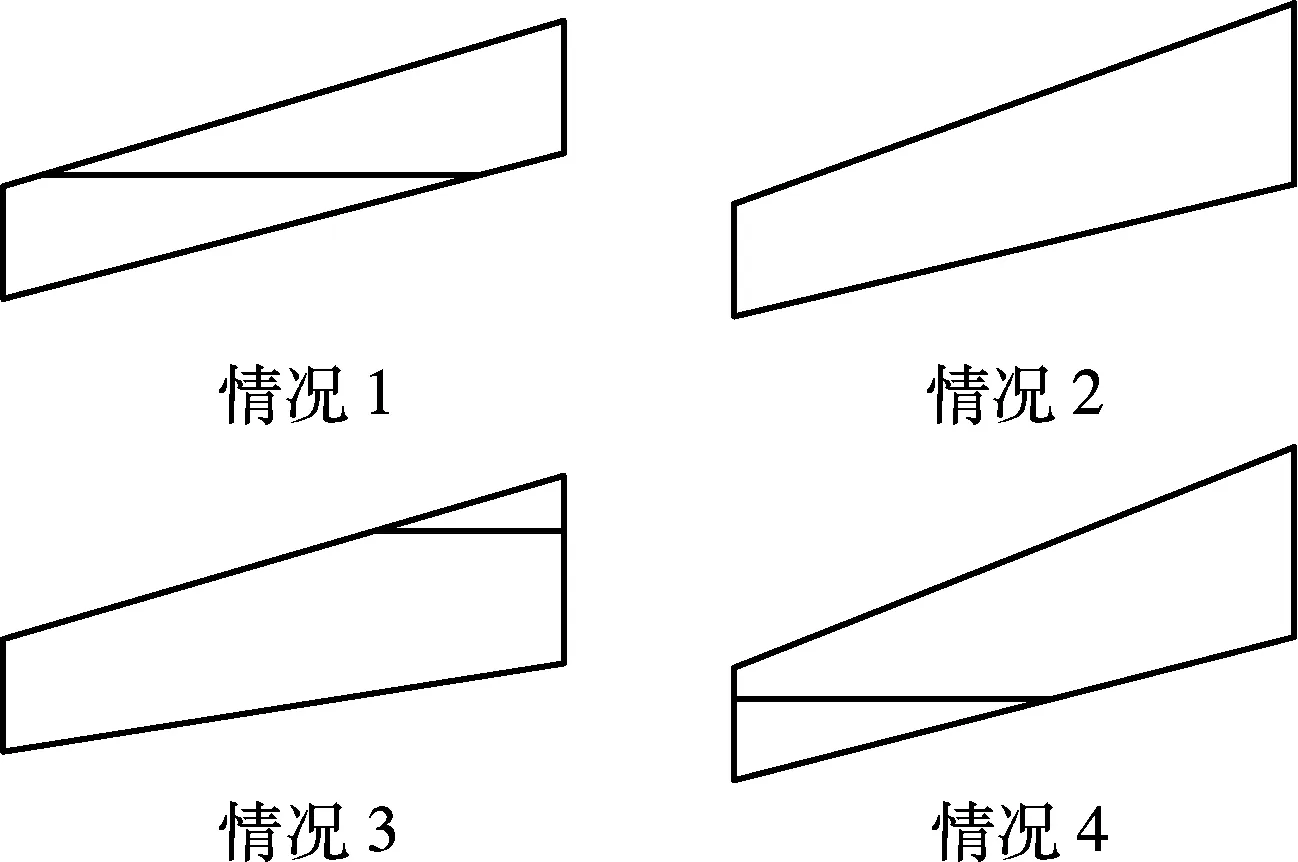
(b) 射线束与像素格相交产生多边形组合的一般情况

相邻射线可能穿过不同的像素格,产生不同的多边形组合(见图3(b))．由图可知,情况1下,射线束穿过2个像素,与像素格相交的区域分别形成2个不规则多边形;情况2下,射线束穿过1个像素,与像素格相交的区域形成平行四边形;情况3和情况4下,射线束穿过2个像素,与像素格相交的区域分别形成三角形和不规则多边形．根据交点坐标值计算面积大小,并将其作为该像素对该射线束的贡献值,即权值aij．继续在各自的交点数组中遍历下一个交点坐标,若一个交点数组优先遍历结束,另一个交点数组需要继续遍历,直到最后一个交点．

除上述讨论的一般情况外,对于一些特殊的个别情况,例如射线斜率为±1、相邻射线从重建区域的不同边界射入等,讨论方法类似．

2　基于字典学习的方法

2.1字典表达

根据稀疏表示理论,信号可通过有限的字典原子的线性组合来表示．因此,图像块可表示为

(5)

给定字典后,需要找到表示图像块x的稀疏表达,即确保稀疏表示系数α中非零个数最少,等价于求解如下的优化问题:

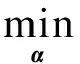
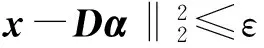
(6)

式中,ε≥0为误差限．

引入拉格朗日常数δ,可将式(6)改写成如下的非约束形式:

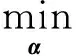
(7)

一般采用贪婪算法(如正交匹配追踪算法[12])来求解式(6)或式(7)．即在迭代过程中,选择与信号残差最匹配的原子,将其正交投影到被选择原子所构成的空间中,重新计算残差信息,直至残差满足预先设定的误差限．

2.2字典学习

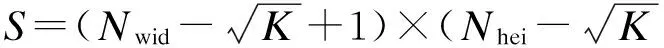
(8)

式(8)等价于求解以下任一目标函数:

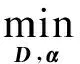
s.t.∀s,‖αs‖0≤T0

(9)

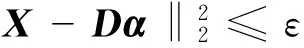
(10)

式中,T0为稀疏度．

本文使用高剂量图像作为训练样本,利用K-SVD算法[13]获取合适的字典．该算法对字典D中的原子逐个进行更新,因此可将式(9)细化到每一个信号,即

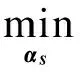
s.t.‖αs‖≤T0

(11)

K-SVD算法的目的在于使得式(11)值最小,联合式(9)和式(11)将目标函数修改为下式进行求解:

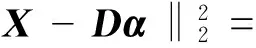
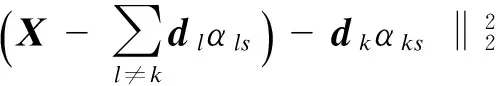
(12)

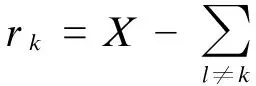
3　基于字典学习的图像重建算法

CT图像重建算法中的迭代重建算法抗噪性能较好,伪影抑制能力较强,并且在无完备投影数据的情况下仍能重建出质量较好的图像,因此得到了广泛的应用．另外,字典学习的方法不仅引入了先验知识,减少了方程数量,还包含了图像的结构信息．将字典学习的方法与图像的迭代重建算法相结合,便可有效实现超分辨率图像重建．图像重建的过程即为求解以下目标函数:

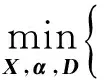
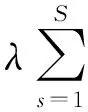
(13)

式中,Es为从离散图像X中提取图像块的矩阵函数,且Es∈RK×N;λ为正则化系数．式(13)中第1项表示最小化计算投影与测量投影之间的差异,为保真项;第2项为使用字典进行图像稀疏分解的先验惩罚项．式(13)的目标函数可分解为如下2个函数交替求解:

1) 固定D和X求解αs,即

(14)

2) 根据字典D和αs更新X,即

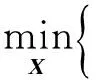
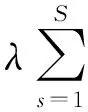
(15)

式(15)为二次凸函数形式,可利用梯度下降法求解．

4　实验

利用本文算法进行超分辨率图像重建,以验证超分辨模型和本文算法的有效性．投影数据由苏州海斯菲德信息科技有限公司HiscanM-1000型小动物CT拍摄小鼠获得．CT扫描管电压为40kV,管电流为200μA．用于重建的投影数据大小为992×360,其中992表示探测器的宽度,360表示投影的角度数．原始重建图像的大小为886×886像素,按照本文模型重建后的图像大小为1 772×1 772像素．为获得高质量的图像以作为训练图像字典的样本,在360°范围内按圆形轨迹扫描方式均匀采集了1 800个角度的投影图,并使用FBP算法重建得到高质量的图像．以8×8像素大小的图像块对该高质量图像进行采样,得到训练集,字典大小设定为64×256,其中64为图像块按行重排为列向量后的行数,256为字典的原子个数．训练时选取的稀疏度为3,迭代次数为20．训练得到的图像字典如图4所示．

图4　基于高质量图像训练获得的图像字典

实验中,设置图像初始值X0=0．计算机配置为Inteli5-2400,3.10GHzCPU．为验证本文算法的性能,将其与以下2种传统的基于插值的超分辨率重建算法进行比较:① 双线性插值后处理算法(简称为算法1),即利用基于面积权值的迭代重建算法得到原始图像,再使用双线性插值算法将图像插值为1 772×1 772像素的图像;② 投影数据一维径向线性插值前处理算法(简称为算法2),即将投影数据在探测器宽度上进行线性插值算法处理,得到1 984×360大小的投影数据,再使用FBP算法重建为1 772×1 772像素大小的图像．

选取不同λ进行对比实验后得出,当λ=1.0时本文算法的结果相对更好．CT图像的数据位数为12,显示窗宽为2 483,窗位为1 434．图5所示为3种算法的重建结果．

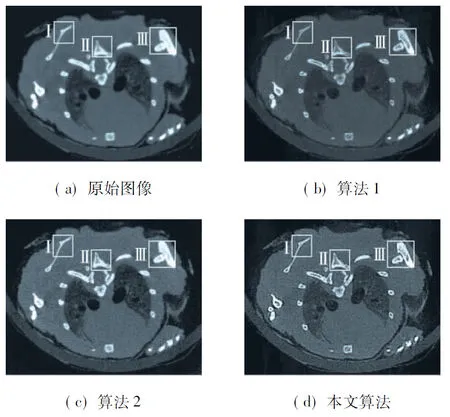
图5　3种算法下小动物CT的重建图像

为更好地观察各算法的重建结果,分别选取图5中代表性区域Ⅰ,Ⅱ,Ⅲ进行放大,结果见图6．图6(a)为原始图像直接放大后的结果,模糊程度较大,很难观察到图像的细节信息,且边缘有锯齿状伪影．图6(b)和(c)分别为基于算法1和算法2的重建图像,具有一定的超分辨率效果,能够观察到被放大后的图像细节,且边缘基本不存在锯齿状伪影;但图像对比度不高,细节信息的层次感不强．图6(d)为基于本文算法的重建图像,与图6(b)和(c)相比,在图像对比度、细节层次的丰富性和边缘保持方面更具有优越性,超分辨率效果更好．

为客观评价算法的性能,分别选取图5中代表性区域Ⅰ,Ⅱ,Ⅲ来计算相邻像素灰度方差(SMD),它是用于衡量图像清晰程度的最常用的评价函数之一[14]．计算结果见表1．由表可见,基于本文算法的重建图像的SMD参数明显高于其他2种算法,表明所得的重建图像清晰度最高．

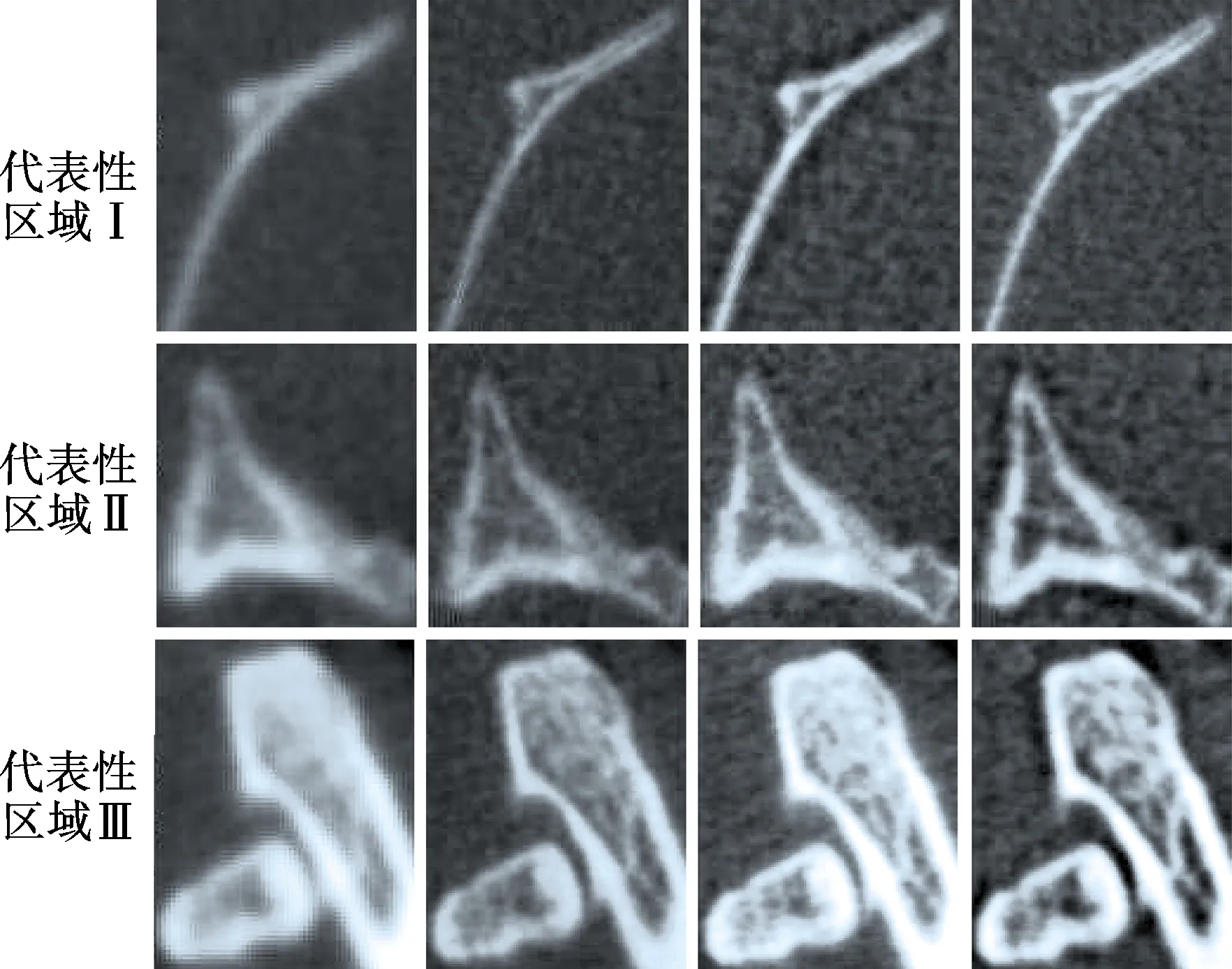
(a) 原始图像　(b) 算法1　(c) 算法2　(d) 本文算法

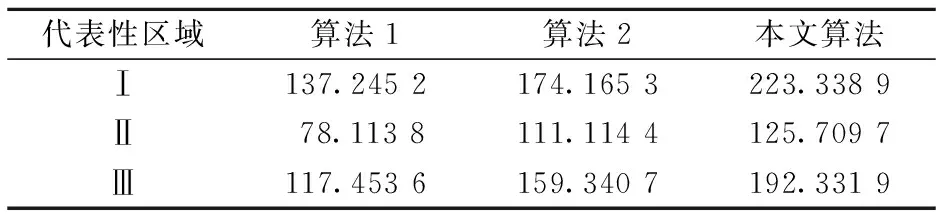
表1　重建图像中3处代表性区域的相邻像素灰度方差

此外,选取各重建图像中多处具有代表性的边缘,计算并绘制了调制传递函数(MTF)[15]曲线,结果见图7．由图可见,基于算法1和算法2的重建图像的MTF曲线下降速度明显快于采用本文算法时的情况,表明利用本文算法得到的重建图像中高频信息保留得最完整,算法的优越性得到进一步验证．

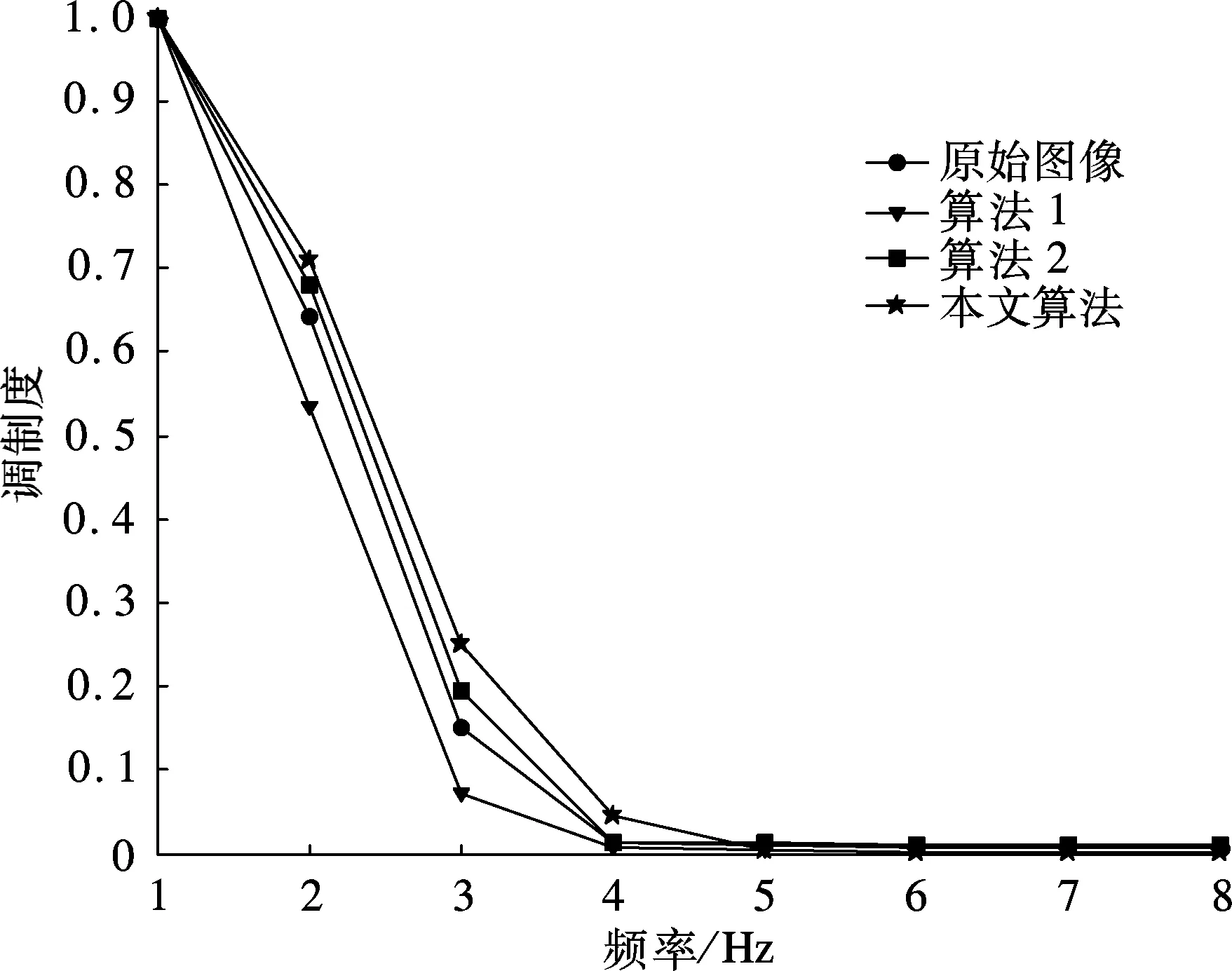
图7　重建图像的MTF曲线

下面利用由苏州海斯菲德信息科技有限公司提供的Hiscan H-100型高分辨率CT拍摄木质牙签获得的投影数据,对3种重建算法的性能进行比较．图8给出了3种算法的重建图像．图9为重建图像中代表性区域Ⅰ,Ⅱ放大后的结果．由图9中箭头所指区域可见,采用本文算法时孔洞结构保留得最清晰、完整．

综上可知,本文算法较其他算法在图像清晰度、细节的完整性和边缘保持方面有比较明显的优势．

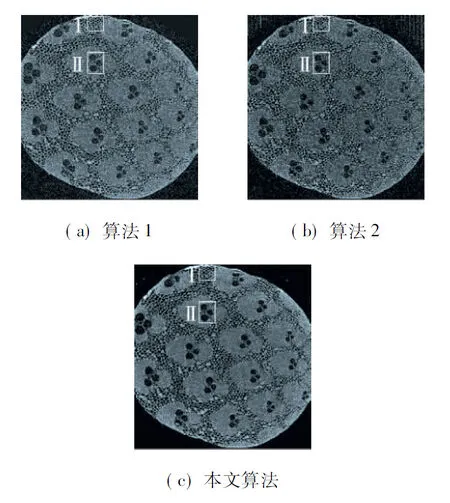
图8　高分辨率CT下3种算法的重建图像

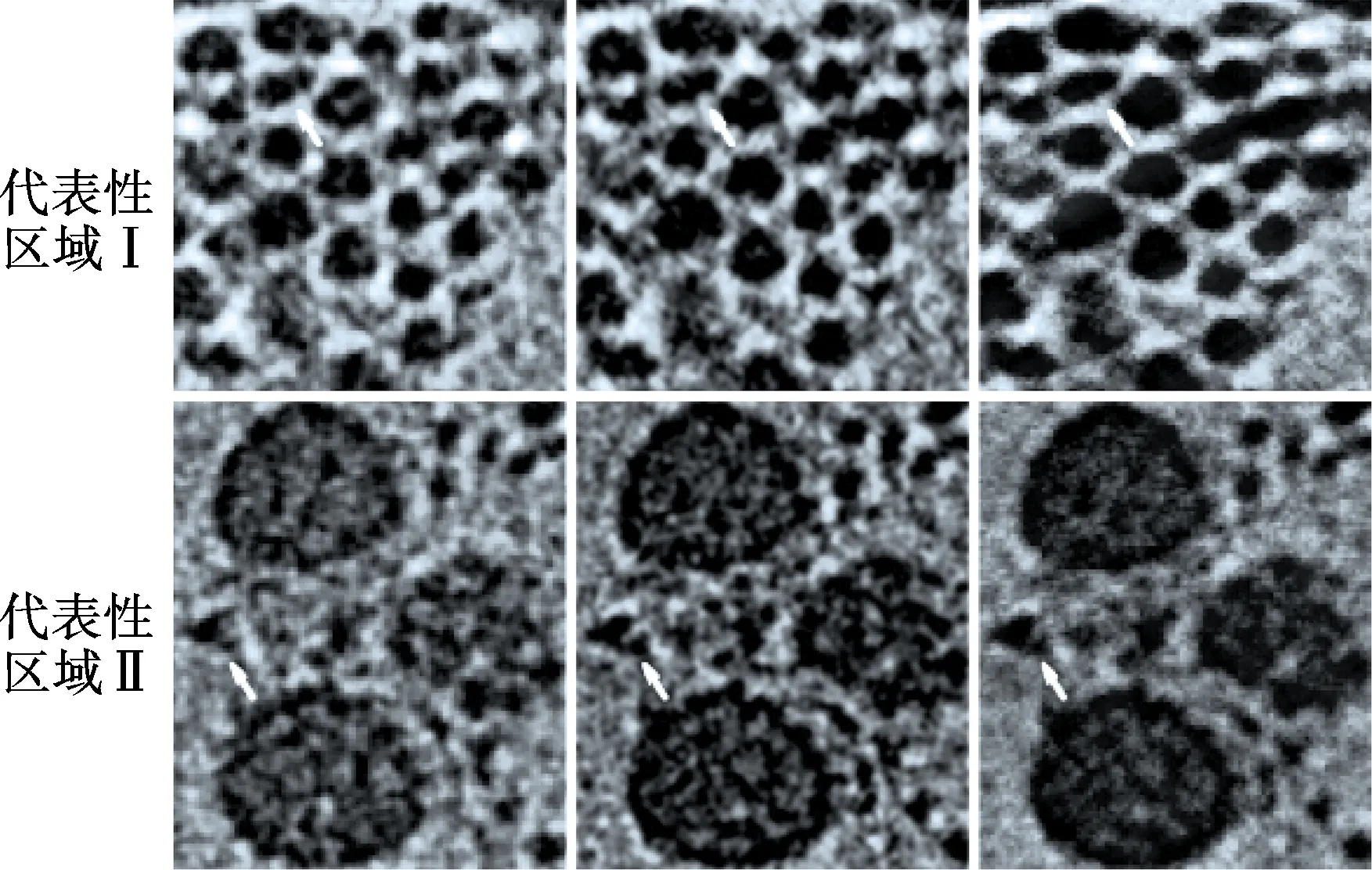
(a) 算法1　　　　(b) 算法2　　　　(c) 本文算法

5　结语

本文将压缩感知理论和图像迭代重建算法相结合,提出了一种基于字典学习的超分辨率重建算法．在无需改变CT的硬件系统、机械结构以及不需要对投影数据插值的情况下,通过将重建图像网格细化,使用字典学习加迭代的方法进行稀疏求解,并在迭代过程中将原始的长度权值转换为精度更高的面积权值,从而获得了分辨率更高的重建图像．实验结果表明,较之传统的基于插值的超分辨率重建算法,本文算法在图像高频信息的保留、图像细节的完整性和边缘保持方面具有优势,从而有效提高了重建图像的空间分辨率．本文算法是在空域上实现的,故而可以扩展到三维锥束模型的求解上,但由此带来的大规模数据量问题和算法效率下降问题有待进一步研究．

References)

[1]Ritman E L. Vision 20/20: Increased image resolution versus reduced radiation exposure[J].MedicalPhysics, 2008, 35(6): 2502-2512.DOI:10.1118/1.2919112.

[2]Park S C, Park M K, Kang M G. Super-resolution image reconstruction: A technical overview[J].IEEESignalProcessingMagazine. 2003, 20(3): 21-36. DOI:10.1109/msp.2003.1203207.

[3]Ffohr T G, Stiemtoffer K, Suss C, et a1.Novel ultrahigh resolution data acquisition and image reconstruction for multi-detector row CT[J].MedicalPhysics, 2007, 34(5): 1712-1723. DOI:10.1118/1.2722872.

[4]魏东波, 傅健, 李斌, 等. 提高三维ICT成像空间分辨率的扫描方式及其重建算法[J]. 航空动力学报, 2007, 22(5): 768-772. DOI:10.3969/j.issn.1000-8055.2007.05.014.

Wei Dongbo, Fu Jian, Li Bin, et al. Scan mode and its reconstruction algorithm for improving spatial resolution of 3D-ICT[J].JournalofAerospacePower, 2007, 22(5): 768-772. DOI:10.3969/j.issn.1000-8055.2007.05.014. (in Chinese)

[5]Lonn A H R. Computed tomography system with translatable focal spot:USA, 5173852[P]. 1992-12-22.

[6]傅健, 谭忍泊, 赵峰. 一种用于CT空间分辨率增强的图像重建方法[J]. 航空动力学报, 2013, 28(5): 971-976.

Fu Jian, Tan Renbo, Zhao Feng. An image reconstruction method for improving CT spatial resolution[J].JournalofAerospacePower, 2013, 28(5): 971-976. (in Chinese)

[7]Freeman W T, Jones T R, Pasztor E C. Example-based super-resolution[J].IEEEComputerGraphicsandApplications, 2002, 22(2):56-65. DOI:10.1109/38.988747.

[8]Wang J, Zhu S, Gong Y. Resolution enhancement based on learning the sparse association of image patches[J].PatternRecognitionLetters, 2010, 31(1):1-10. DOI:10.1016/j.patrec.2009.09.004.

[9]Jeong S C, Song B C. Fast super-resolution algorithm based on dictionary size reduction usingk-means clustering[J].ETRIJournal, 2010, 32(4): 596-602.

[10]Gilman A, Bailey D G, Marsland S R. Interpolation models for image super-resolution[C]//The4thIEEEInternationalSymposiumonElectronicDesign,Test&Applications. Hong Kong,China, 2008: 55-60. DOI:10.1109/delta.2008.104.

[11]王丽艳, 韦志辉, 罗守华, 等. 压缩感知在Micro-CT图像超分辨重建中的应用[J]. 中国图象图形学报, 2012, 17(4): 487-493.

Wang Liyan, Wei Zhihui, Luo Shouhua, et al. Image super reconstruction for micro-CT based on compressed sensing[J].JournalofImageandGraphics, 2012, 17(4): 487-493. (in Chinese)

[12]Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].IEEETransactionsonInformationTheory, 2012, 58(2): 1094-1121.

[13]Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing over-complete dictionaries for sparse representation[J].IEEETransactionsonSignalProcessing, 2006, 54(11): 4311-4322. DOI:10.1109/tsp.2006.881199.

[14]Jarvis R A. Focus optimization criteria for computer image processing[J].Microscope, 1976, 24(2): 163-180.

[15]American Society for Testing and Materials(ASTM). E1441-00(2005) Standard guide for computed tomography(CT) imaging[S]. West Conshohocker, Pennsylvania,USA: ASTM, 2005.

Super-resolution image reconstruction for micro-CT based on dictionary learning

Yao Jiali Li Zhongyuan Wu Huazhen Li Guang Luo Shouhua

(School of Biological Sciences and Medical Engineering, Southeast University, Nanjing 210096, China)

To improve the spatial resolution of reconstructed images for micro computed tomography(micro-CT), a super-resolution image reconstruction algorithm based on dictionary learning is proposed. First, the reconstructed image grid is refined and the area weight model is used to achieve accurate modeling of the projection process. Then, high quality images are selected as the training samples. The K-means singular value decomposition (K-SVD) algorithm is adopted to train the image dictionary. On the basis of the image dictionary, the orthogonal matching pursuit algorithm is used to implement sparse representation of the reconstructed image, which is introduced into the objective function of the reconstruction algorithm as a sparse constraint. Finally, the gradient descent method is adopted to solve the objective function. The experimental results show that compared to the conventional interpolation-based super-resolution reconstruction algorithms, the proposed algorithm has advantages on the image contrast and the edge preservation, and retains more high frequency information of images, effectively improving the spatial resolution of the reconstructed images.

super-resolution reconstruction; dictionary learning; area weight; micro computed tomography(micro-CT)

10.3969/j.issn.1001-0505.2016.05.010

2016-01-06.作者简介: 姚佳丽(1991—)，女，硕士生；罗守华(联系人)，男，博士，副教授，luoshouhua@seu.edu.cn.

国家自然科学基金资助项目(61127002，61179035).

TP391.1

A

1001-0505(2016)05-0957-07

引用本文: 姚佳丽,李中源,吴华珍,等.基于字典学习的超分辨率显微CT图像重建[J].东南大学学报(自然科学版),2016,46(5):957-963. DOI:10.3969/j.issn.1001-0505.2016.05.010.