纳米磁粒子磁矩翻转模型与星形线的计算

杨　柳，孙玉泉，文　晓

（北京航空航天大学　数学与系统科学学院，北京　100191）

纳米磁粒子磁矩翻转模型与星形线的计算

杨柳，孙玉泉，文晓

（北京航空航天大学数学与系统科学学院，北京100191）

在微积分中有许多关于星形线的计算问题，本文通过介绍一个关于星形线的应用实例，说明星形线来源于实际的应用具有重要的应用价值，在此基础上我们对相关的计算问题进行归纳和总结.

星形线；定积分应用；纳米磁畴；磁矩翻转

星形线、心形线、笛卡儿叶形线等是微积分中常见的一些特殊的曲线，在数学中我们经常进行一些与这些曲线相关的计算.实际上这些曲线都有一定的应用背景，来自于实际的应用问题，在分析相关问题时具有重要作用.下面我们通过一个来自于相关领域前沿研究中的实际问题，给出一个与星形线相关的应用背景，说明这些曲线不只存在于微积分相关的计算当中.

1　磁畴磁矩的翻转模型

纳米单磁颗粒磁矩在磁场的影响下可以改变和保持其定向的性质是现代磁记录产业的基础.这一原理在信息存储和生物医学等方面都起着重要作用［1,2,3,4,5,6］.下面我们来介绍一下纳米单磁颗粒磁矩在磁场的影响下方向变化的模型，首先假设研究球形的单畴粒子，具有单轴各向异性，易磁轴方向为z轴.

用M表示该粒子的磁矩，根据上面的假设，当该粒子不受外界影响时，各项异性能关于易磁轴对称，因此仅和磁矩在z轴上的分量有关，自由能量可表示为：

其中是粒子的体积，为各项异性常数，单位为.当时，该能量在M与z轴夹角为0和时最小，在夹角为时能量最大.

图1　能量密度分布［2］

当粒子的磁矩达到平衡状态时，其磁矩会指向使其能力最低的方向，当0和为最小能力方向时，这两个方向就是磁矩的稳定方向.

当粒子到外磁场H中时，磁场产生的磁场能为-μ0M· HV0，其中常数是磁导率.此时该粒子具有的总能量为：

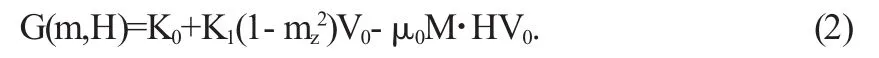
根据粒子达到平衡状态时，磁矩指向使其能力最低的方向这样性质，当粒子受到外磁场影响时其能力最低点和磁矩方向会发生相应的变化.下面我们就分析外加磁场对能力最低点的影响.为了表示方便，我们将能力进行相应的无量纲的变换.因为我们只关心G（m,H）的最值点的变化，因此，我们忽略掉（2）式中的常数项，并除以适当的常数可得到

其中m是与磁矩M同方向的单位向量，ha是和磁场H同方向的向量.

在单项各向异性的条件下，由于对称的原因，在平衡状态下磁化强度在于易磁轴z轴和外磁场ha所确定的平面内.因此使用球坐标表示，令m与z轴夹角为θ，ha与z轴夹角为θh，则有：

将（3）式表示为：

其中haz=hacosθh，ha⊥=hasinθh分别是ha在z轴的平行和垂直分量.

如前所述在ha=0时，能量在θ=0时最小，因此这是一个平衡位置，同样的相反方向θ=π也是平衡位置.当时，能量值取得最大.现在，如果我们运用一个和最初磁化相反的小的外部磁场（θ=0或π）.当ha逐渐增大时会达到一个最大值和一个最小值消失的临界位置.对于这一临界状态的ha取值记做hSW.当ha＞hSW时，自由能将只存在一个最小值和一个最大值.这就意味着当磁场ha＜hSW时，粒子将保持在沿着z轴的初始位置，而一旦ha＞hSW，对应于逆转方向，磁场将转变为只剩下一个最小能量，此时磁化方向将发生翻转.

下面我们分析当ha与z轴的夹角不是零时，其临界值的变化情况.显然临界磁场hSW是θh的函数，或者haz和ha⊥表示的直角坐标下的函数.临界点构成了存在两个最小值的区域和只存在一个最小值的区域之间的分界线.在（5）式中将haz和ha⊥看作参数，θ为自变量，临界点必然满足：

通过求解方程组（6），可以得到下面的等式：

将haz和ha⊥看作函数，θ为参数，可得表达式

由上面等式所定义的曲线如图2所示：

图2　在平面haz和ha⊥上的Stoner-Wohlfarth星形线

这正是我们熟悉又陌生的星形线.

由极坐标表示可以得到：

特别地当θh=0时，可以很容易的验证

因此，当外磁场分量对应的点（ha,ha⊥）位于星形线以外，则只有一个最小能点存在，当该点不是初始平衡点时，磁化方向将会发生改变.相反的，当磁场对应的点（ha,ha⊥）位于星形线以内，仍然存在自由能的两个最小值，即两个稳定的平衡.

这个磁化运动的动力学模型说明，星形线和我们在微积分中遇到的大部分问题一样，它不是我们为了做题而凭空创造的产物.这些问题大都来源于实际的问题，并且对分析和解决问题有着非常重要的作用.

2　星形线计算问题

下面我们总结一下与星形线相关的计算问题，为了计算方便我们统一使用下面的表达式：

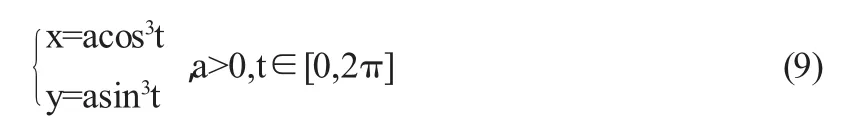
（1）星形线所围的面积：

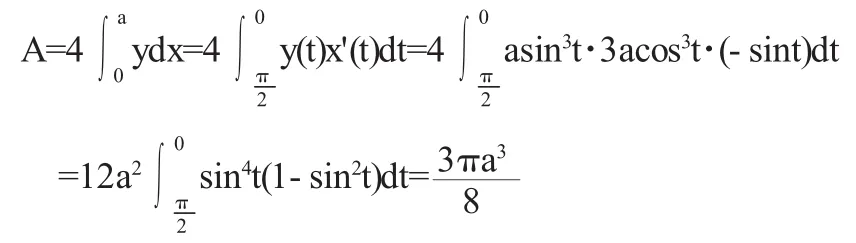
（2）星形线的周长：

（3）星形线绕x轴的旋转体体积：

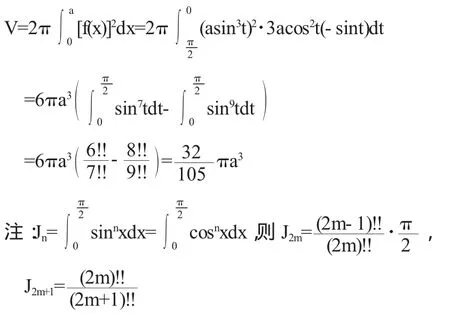
（4）星形线绕x轴的旋转曲面面积：

〔1〕Bean C P，Livingston J D.Superparamagnetism［J］.Journal of Applied Physics，1959，30（4）：S120-S129.

〔2〕d’Aquino M.Nonlinear magnetization dynamics in thinfilms and nanoparticles［D］.PhD thesis，Universitadeglistudi di Napoli“Federico II”，Facolta di Ingegneria，2004.URL http://www.fedoa.unina.it/148，2004.

〔3〕Liu Y，Sellmyer D J，Shindo D.Handbook of Advanced Magnetic Materials：Vol 1.Nanostructural Effects.Vol 2.Characterization and Simulation.Vol 3.Fabrication and Processing.Vol 4.Properties and Applications［M］.Springer Science&Business Media，2008.

〔4〕GuimarãesAP.Principlesofnanomagnetism［M］.Springer Science&Business Media，2009.

〔5〕Pankhurst Q A，Thanh N T K，Jones S K，et al.Progressinapplicationsofmagneticnanoparticlesin biomedicine［J］.Journal of Physics D：Applied Physics，2009，42（22）：224001.

〔6〕Pankhurst Q A，Connolly J，Jones S K，et al.Applications of magnetic nanoparticles in biomedicine［J］.Journal of physics D：Applied physics，2003，36（13）：R167.

O172.2

A

1673-260X（2016）09-0001-02

2016-06-18

国家自然科学基金（11201020）；北京航空航天大学教学改革项目（4303006）