伽利略相对运动变换式的理解与记忆

周建芳，袁五届，张金锋，尹新国

（淮北师范大学　物理与电子信息学院，安徽　淮北　235000）

伽利略相对运动变换式的理解与记忆

周建芳，袁五届，张金锋，尹新国

（淮北师范大学物理与电子信息学院，安徽淮北235000）

在绝对时空观下，相对运动满足伽利略变换式，该内容一直是大学物理课程教学的重点和难点.结合多年的教学经验，本文分别对伽利略相对运动变换式的理解与巧妙记忆进行了探讨，创新性地提出了三种帮助理解与记忆的方法.本文的研究，将对学生深刻地理解和牢固地掌握伽利略相对运动变换式具有一定的指导作用，对教师的课堂教学与复习巩固也具有一定的参考价值.

相对运动；伽利略速度变换；伽利略加速度变换

1　引言

当研究问题所涉及的运动速度远小于真空中光速（3×108米/秒）的条件下，时间与空间具有绝对性，即时间流逝与空间距离不依赖于参考系的选择，这种绝对时空观与日常经验相符合.在这样的绝对时空观下，同一个物体的运动在不同运动着的参考系下，他们运动的描述是不同的，即运动的描述具有相对性.目前，在很多大学物理教材以及一些期刊论文中很容易推导出这种相对运动满足伽利略变换关系［1-3］；但是，如何选择两个相对运动的坐标系，学生往往存在误区，如何深入地理解伽利略速度变换式和伽利略加速度变换式的物理含义，如何巧妙地记忆变换式的各种形式，在已有的教材中讲解甚少.根据本人多年的教学经验，分别对这两种变换式的理解和记忆作如下深入探讨.

2　变换式的理解与记忆

一个运动的物体A在两个相互平动的参考系K与K'下,他们相对运动的描述满足如下的伽利略变换式［1,2］：

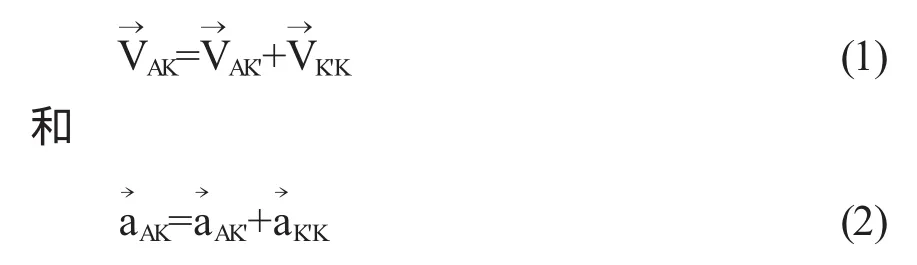
2.1理解

一些教材在推导伽利略变换式（1）和（2）时，常选择静止的坐标系为K，运动的坐标系为K'，从而得到运动的绝对量、相对量和牵连量之间的变换关系，具体变换关系如下［1,2］：

这里绝对量表示物体A相对于静止坐标系的值，相对量表示物体A相对于运动坐标系K'的值，牵连量表示运动坐标系K'相对于静止坐标系K的值.对于（3）和（4）的理解，由于坐标系K与K'之间是相互运动的，K'也可以认为是静止的，而K认为是相对K'反向运动的，从而学生在选择K与K'时，很容易混淆绝对量与相对量，牵连量也容易错选为反向［4,5］.所以，在教学中，更建议初学者用带有明确下标注的变换式（1）和（2），慎用变换式（3）和（4）.

尤其要注意的是，对于变换式（1）与（2），学生经常误认为K一定要为静止坐标系，其实K也可以是运动坐标系，所以，K与K'的选择可以是任意的.另外，对于运动的物体A如果可看作质点或是可看作只有平动没有转动的刚体，那么A与两坐标系（参照物）K与K'的选择也都是任意的，我们可根据解题的方便任意选择A、K与K'.

2.2记忆

结合多年的教学经验，本文提出了如下三种帮助理解和记忆的方法.

方法1：加法原则［重写（1）与（2）］：

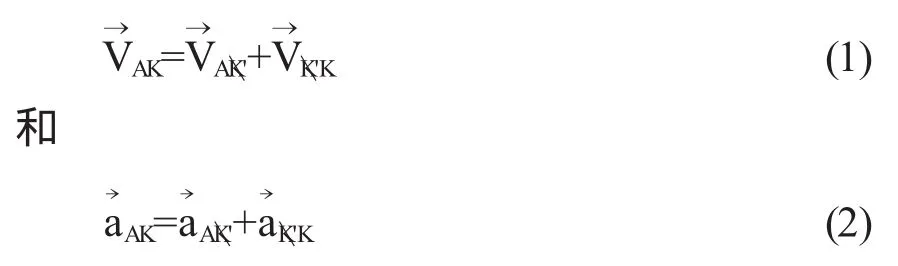
变换式（1）与（2）的右边分别表示两项速度与两项加速度相加，等式中下标注A、K、K'任意两者互换后等式仍成立.根据下标注，我们可以这样加强上述加法原则的记忆：等式右边前一项下标注的第二个字母与后一项下标注的第一个字母相同并可抵消，剩下的两字母即为变换式左边的下标注.

方法2：减法原则［变换（1）与（2）］：

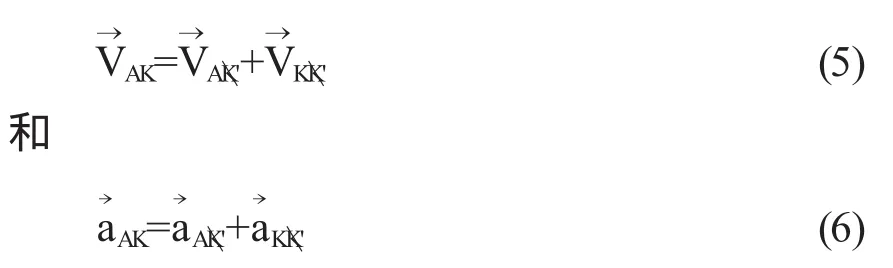
变换式（5）与（6）的右边分别表示两项速度与两项加速度相减，等式中下标注A、K、K'任意两者互换后等式仍成立.根据下标注，我们可以这样加强上述减法原则的记忆：等式右边前一项下标注的第二个字母与后一项下标注的第二个字母相同并可抵消，剩下的两字母即为变换式左边的下标注.

方法3：下标注相减原则：

对于等式（1）、（2）、（5）、（6）或它们变换后的各种形式，均可根据如下的下标注相减原则加强记忆：等式右边所有项下标注的两字母写成第一个字母减第二个字母，然后再根据项的加或减进行相应的加减运算，最后得到相减的两字母即为等式左边的下标注.以等式（1）和（5）为例.对于等式（1），右边下标注字母（A-K'）+（K'-K）=A-K，即得到等式左边的下标注AK；对于等式（5），右边下标注字母（A-K'）-（K-K'）=A-K，即得到等式左边的下标注AK.

3　总结

对于伽利略速度变换与加速度变换，形式的选择灵活多样，正确的选择变换形式是求解问题的关键和前提.本文对伽利略相对运动变换式进行了深入的理解和探讨，并创造性地提出了帮助理解和记忆的三种方法：加法原则、减法原则以及下标注相减原则.为了学生能够很好地理解和掌握伽利略相对运动变换，在讲授完变换式的推导后，教师要及时地对变换式的理解和记忆进行剖析，并辅助于典型例题，安排两到四个例子进行讲解.本文的研究，将对学生牢固地掌握伽利略相对运动变换具有一定的指导作用，对教师的课堂与复习教学也具有一定的参考价值.

〔1〕胡盘新，汤毓骏，钟季康.普通物理学简明教程（第二版，上册）［M］.北京：高等教育出版社，2007.

〔2〕孙厚谦.大学物理（第一版，上册）［M］.湖南师范大学出版社，2014.

〔3〕王墨林.相对运动与速度相加原理［J］.物理教师，2013，34（10）：85-86.

〔4〕杨庆怡.相对运动的描述及相关问题的处理［J］.广西大学学报（自然科学版），2006（31）：184-185.

〔5〕杨勇.论质点的绝对运动、相对运动、牵连运动［J］.科教文汇，2014（295）：49-50.

G642.3

A

1673-260X（2016）09-0005-02

2016-05-11

安徽省自然科学基金项目（1508085MA04）；安徽省高等学校自然科学研究项目（KJ2015ZD33，KJ2016B006）；安徽省高校优秀青年人才支持计划重点项目（gxyqZD2016410）；淮北师范大学教研项目（jy14142，jy13234）；人社部和人社厅联合资助的留学回国人员择优资助项目