基于弹塑性压力中性层偏移的棒材二辊矫直回弹模型

马自勇，马立峰, 2，黄庆学，马立东，楚志兵，黄志权



基于弹塑性压力中性层偏移的棒材二辊矫直回弹模型

马自勇1，马立峰1, 2，黄庆学1，马立东1，楚志兵1，黄志权1

(1. 太原科技大学山西省冶金设备设计理论与技术重点实验室，山西太原，030024；2. 吉林大学超塑性与塑性研究所，吉林长春，130000)

基于二辊矫直变形工艺特点和弹塑性压力中性层偏移理论，确定应力中性层的位置；在考虑中性层偏移和材料硬化的条件下，结合二辊矫直理论和矫直变形应力−应变关系，提出新的双线性矫直拟合方法；在此基础上利用微元法对棒料内部的金属进行弹塑性变形分析，给出新弯矩比公式的同时，提出中性层偏移半径比的概念；最后，结合纯弯回弹理论建立棒料矫直挠度回弹数学模型，并就中性层偏移对棒料矫直回弹影响进行实验分析和验证。实验结果表明：回弹理论计算值与实验数据吻合较好，其最大相对误差为6.45%，明显低于忽略中性层偏移时的相对误差31.65%，证明了理论分析的正确性和模型的有效性。

棒材矫直；中性层偏移半径比；回弹模型；实验分析

随着石油、船舶、汽车等制造行业的飞速发展，对高强度合金钢棒材的需求量和质量要求日益提高，其中直线度要求达到1 mm/m，甚至小于0.5 mm/m，否则后续加工中材料的去除量非常大，损耗严重，成本急剧增加，因此，对棒料矫后直线度的要求十分严格。二辊矫直作为棒料精整的最后一道工序，是保证棒料矫后直线度指标的关键技术。二辊矫直是一个复杂的弹塑性变形过程[1]，存在部分弹性变形，在卸载后弹性变形会立即恢复原态，出现回弹现象。回弹的结果使得棒料的残余曲率发生严重变化，降低棒料的直线度，得到的棒料矫后直线度大于1 mm/m。由矫直曲率比公式[2]可知，无论是板料还是管棒材的矫直均是利用回弹来实现的。回弹量决定了矫直辊辊形的设计和工艺参数的制定，回弹量的预测精度也通过反弯量来影响棒料的残余挠度，最终得到高质量的矫直棒料，因此，准确有效地预测回弹是获得稳定的高精度棒料的基础。对于回弹问题，诸多学者进行了大量的研究[3−14]，但在预测棒料回弹量时都未考虑中性层偏移对回弹的影响，得到的回弹计算模型精度不高。官英平等[15]研究表明，在一定相对圆角半径下，中性层内移对板料弯曲回弹的相对误差可达70%以上。相对于纯弯曲中性层偏移计算，运用本文的弹塑性压力中性层偏移理论计算精度至少提高了3.46倍。因此，本文作者基于棒料二辊矫直变形特点和弹塑性压力中性层偏移理论，结合材料硬化规律和棒料弹塑性变形的力学关系，推导出棒料矫直过程中的挠度回弹计算模型，提出中性层偏移半径比的概念，分析了中性层偏移对回弹计算精度的影响，为后续深入研究高强度合金钢棒材矫直机理和矫直辊辊型优化设计与工艺模型的建立提供数据基础。

1 棒料矫直挠度回弹模型的建立

1.1 基本假设

1) 变形前后棒料的横截面仍保持为平面，垂直于棒材轴线，且截面不发生畸变，截面上应变为线性分布。

2) 棒料是连续均质的弹塑性体，且弹性变形为线性，符合Hooke定律并认为塑性流动符合经典弹塑性理论的卸载规律。

3) 棒料在矫直过程中忽略截面的变形，并认为应变中性层与应力中性层重合。

4) 满足塑性变形体积不变原则, 并且拉压变形部分金属的硬化规律相同，即应力−应变关系一致。

矫直过程中，棒材旋转前进受凸辊压弯，并在压弯处产生塑性压缩(下阴影部分)与拉伸(上阴影部分)变形，如图1所示。在弹塑性变形区外层，切向应变为拉应变，切向应力为拉应力；变形区内层，切向应变为压应变，切向应力为压应力[16]。由假设3)知径向应变；同时各纤维间压应力可以忽略不计，因此，棒材矫直过程应力−应变状态如图2所示。

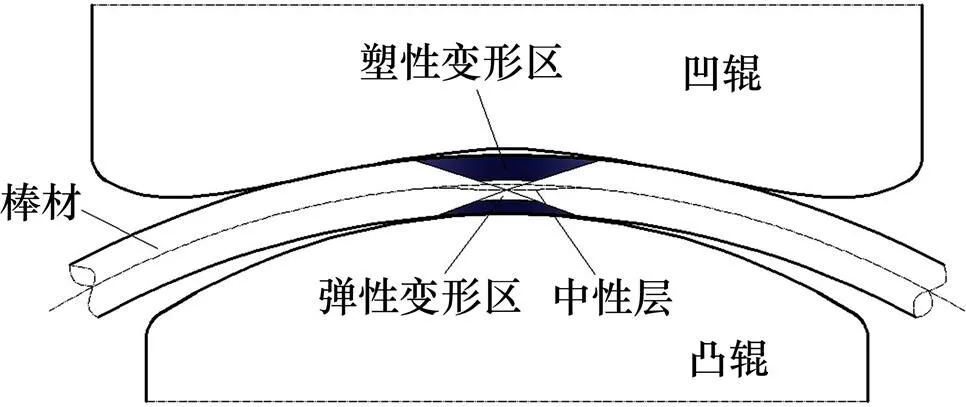
图1 棒材矫直弹塑性变形区域

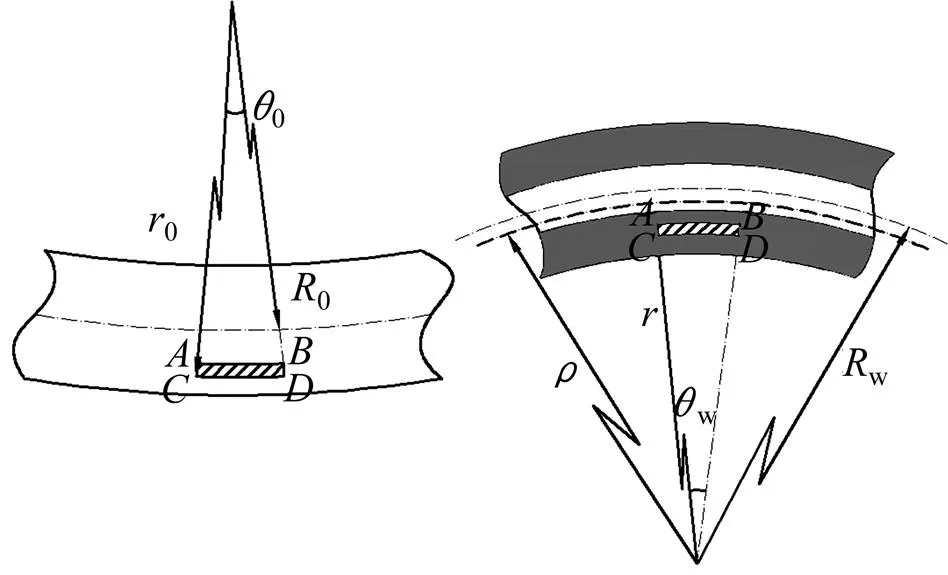
图2 棒材矫直变形区应力−应变示意图

1.2 基于弹塑性压力的中性层偏移分析

1.2.1 中性层偏移几何应变分析

进入矫直工序前，棒料在长度范围内基本都存在径向任意方位的弯曲，其弯曲程度各不同，但它们都会在矫直辊中央段统一为相同方位的弯曲，呈现扁担弯形态，为了便于理论分析，一般将初始弯曲简化为扁担形式的弯曲。现假设微元体起初为拉伸状态，则矫直反弯后该位置处于压缩状态，如图2所示。由于被矫直的棒料原始弯曲程度不大，可认为棒料中性层与几何中心轴是重合的，则棒料中性层处金属纤维原始长度0为

式中：0为初始弯曲半径；为微元体初始弯曲角；

式中：0为微元体初始弯曲半径。

棒材微元体被反弯后中性层长度w为

式中：为微元体所处位置半径。

棒材在反弯前后中性层的长度不变，即

最终

式中：w为反弯半径。

1.2.2 中性层偏移塑性变形应力−应变分析

由增量理论[17]

可得到塑性变形应力关系：

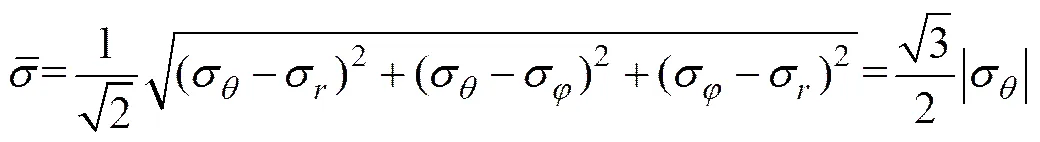
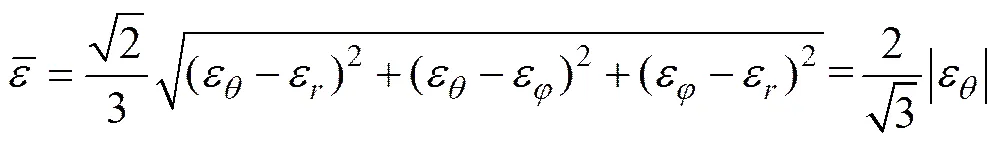
塑性变形拉伸区切向应力分布函数[18]为

定义势函数1为

边界条件为

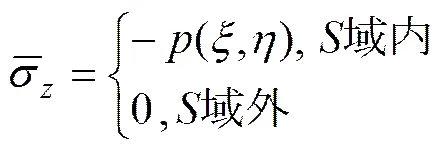
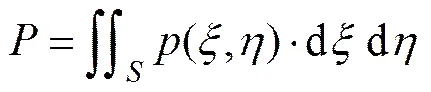
定义的势函数可简化为

凸辊对棒材施加的矫直压力与塑性区径向应力的关系为

1.2.3 基于弹塑性压力的中性层位置确定

同时，

联立消去得：

由于理论推导过程中使用半空间假设，与棒材在凸辊上的接触情况有差异，因此，使用修正系数，得

1.3 内弯矩分析

棒材矫直过程中应力−应变分布如图4所示。

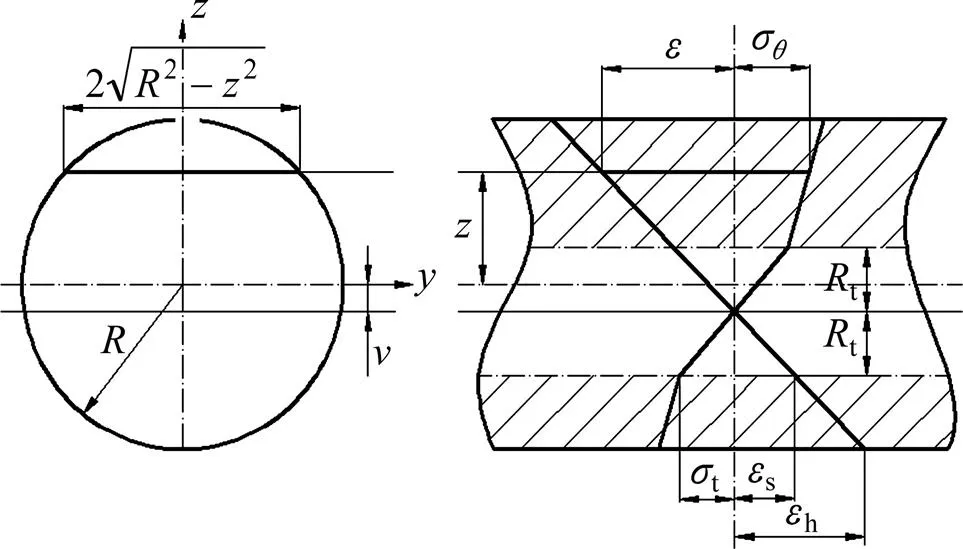
图4 棒材矫直应力−应变图

听中，充分利用暂停键，让学生选答案，较容易的可以复述整个句子，较难的提取关键词，并对照原文再听一遍。对于关键信息，涉及听力场景词，或者影响做题的句子，学生听不出来的，先提取关键词，然后连词成句，比对原文，勾出错误的地方，再听一遍，直至听出为止。这有利于培养学生抓取关键信息的听力，同时有助于听辨能力的培养。

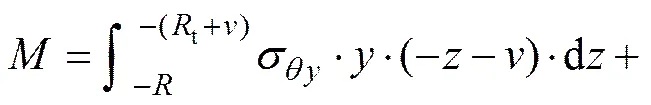
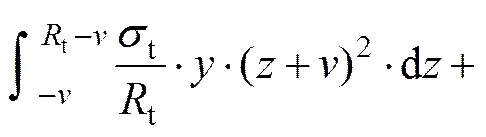
将式(25)化简得

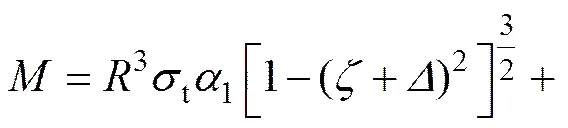
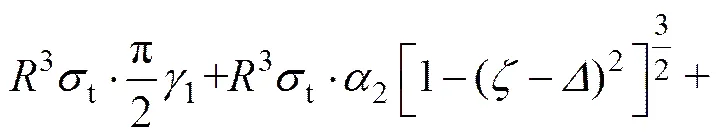
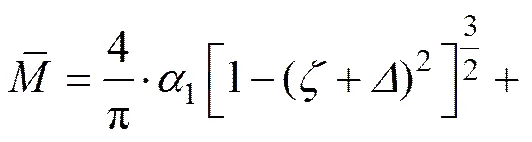
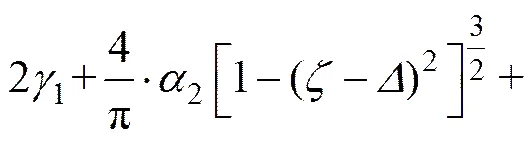
式中：

1.4 回弹模型推导

由于棒材在进入矫直机前存在一定的原始挠度，根据平面假设知，棒材截面处有初始应变

棒材微段弯曲过程示意图如图5所示。根据基本假设1)和初始当量应变定义，棒材微段截面上任意点的弹性弯曲应变、加载后应变及卸载后残余应变分别为

式中：为弹性模量；为棒材断面对轴的惯性矩。

在加载和卸载过程中，

将式(29)~(31)代入式(33)可得：

(a) 初始曲率；(b) 反弯曲率；(c) 残余曲率(与初始曲率反向)；(d) 残余曲线(与初始曲率同向)；(e) 弹性曲率

图5 棒材微段弯曲过程示意图

Fig. 5 Bending process diagram of bar micro-segment

因此，棒材矫直回弹挠度计算模型为

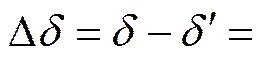
式中：为三点弯曲中两端点间的距离。

2 棒材矫直回弹挠度实验

2.1 实验路线及目的

在WAW1000万能试验机进行拉伸试验，得到40Cr和42CrMo合金钢2种棒材的室温拉伸应力−应变曲线，利用Origin软件对所得曲线进行线性拟 合，为挠度回弹计算模型构建提供参数支持。弯曲试验在10 t液压式压力试验机上进行，通过测量棒材跨中反弯和回弹后的挠度值来验证挠度回弹计算模型的准确性。

2.2 室温单向拉伸实验

通过拉伸实验可以获得材料的屈服强度、伸长率和抗拉强度等参数，这些参数是影响棒材回弹的重要因素。本文以40Cr和42CrMo棒材为例进行拉伸实验，得到其应力−应变曲线如图6所示。

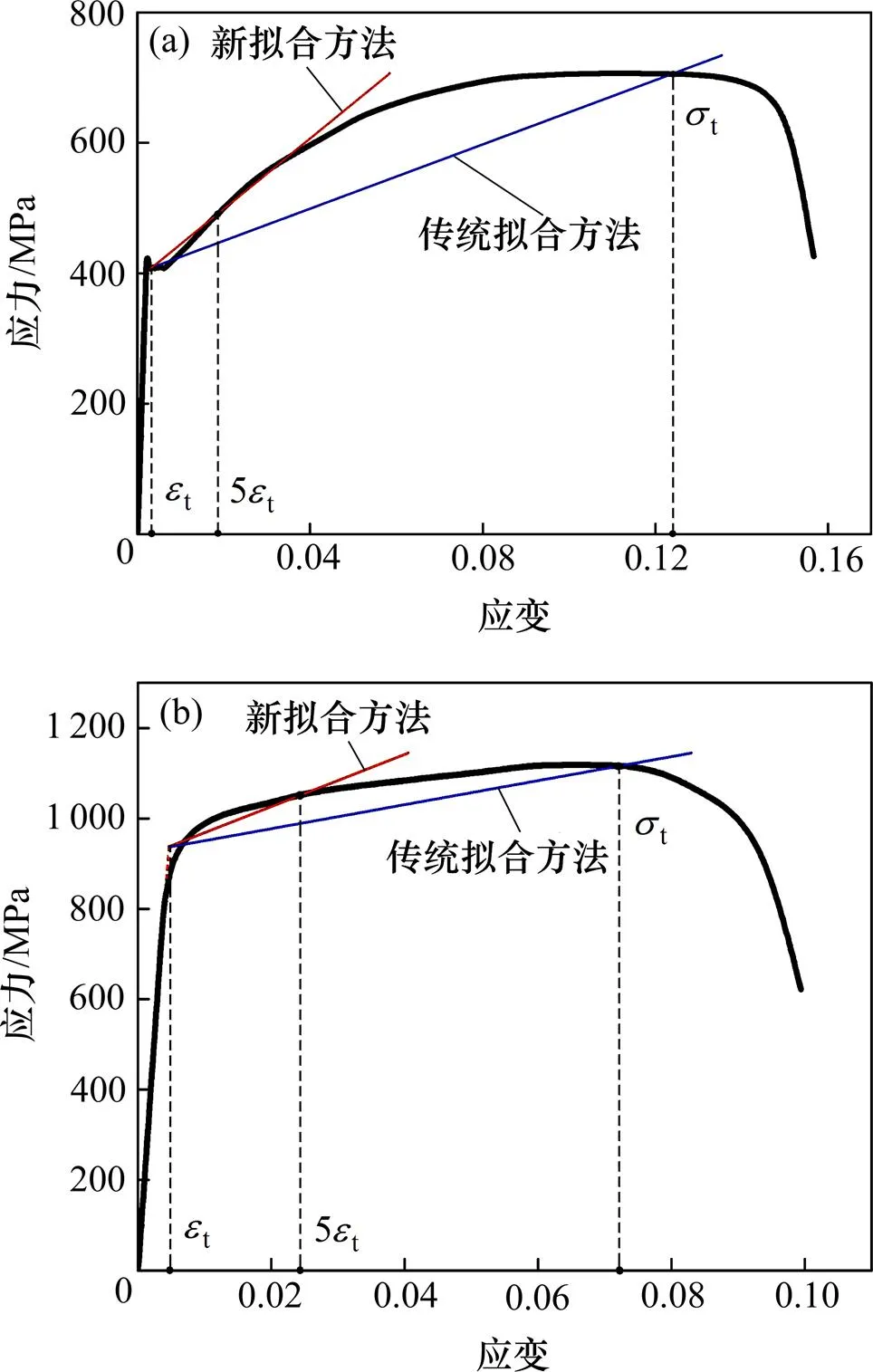
(a) 40Cr；(b) 42CrMo

表1 不同材质的力学性能

2.3 弯曲实验

采用棒材弯曲回弹测试对棒材挠度进行测试，测试方案如图7所示，百分表用于测定棒材跨中的位移。

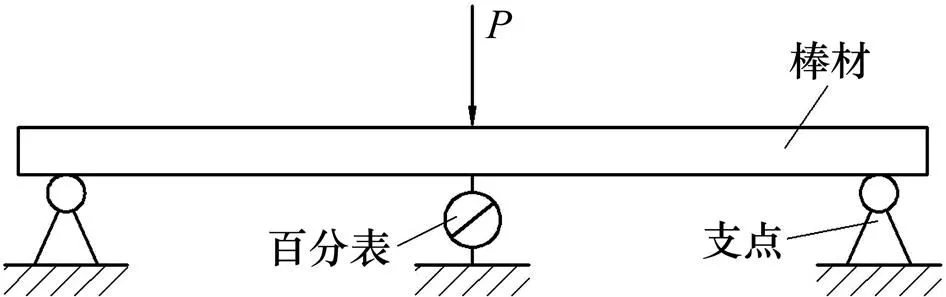
图7 挠度测量示意图

40Cr压下量分别为10，15，20和30 mm；42CrMo压下量分别为10，15和20 mm。每次压下速度为10 mm/min，压下动作完毕后，用百分表测量跨中位移3次并记录取平均值，测量记录完成就开始卸载，卸载速度为100 mm/min。

对棒材进行弯曲试验，载荷−位移曲线如图8所示，在开始的弹性阶段，载荷和位移呈明显的线性变化关系。随着载荷的增加，棒材跨中位移不断增加，当载荷增大到18 kN左右时，棒材开始屈服，之后棒材跨中位移的增加速度迅速增大，而载荷的增加速度则减缓。当位移增加至30 mm和20 mm时，开始卸载。将实验所得数据整理计算即可得到棒材弯曲的回弹值，结果见表2。

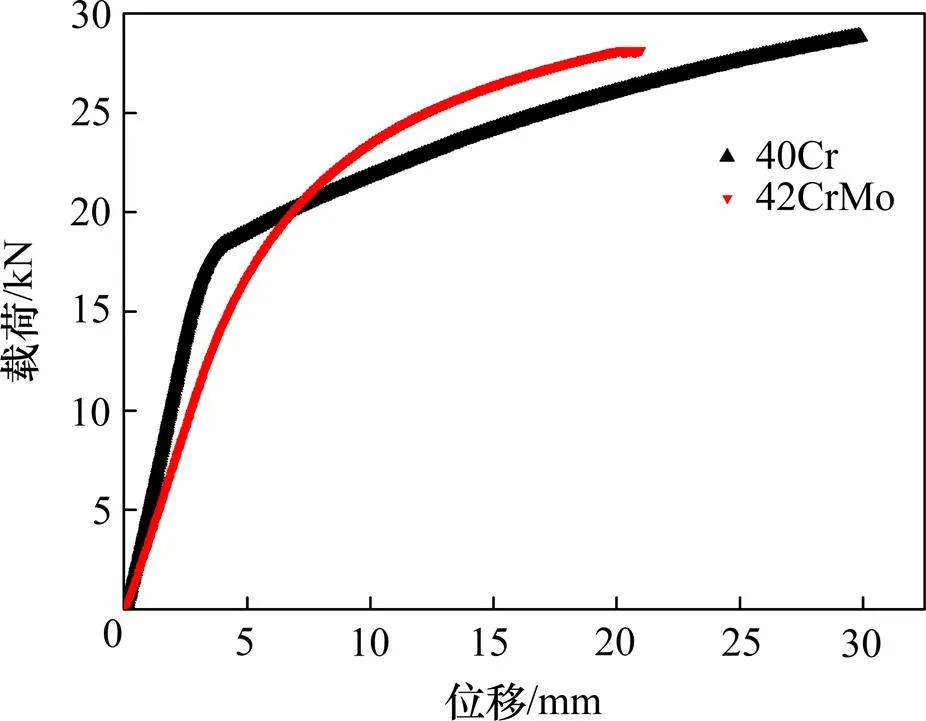
图8 载荷−位移曲线

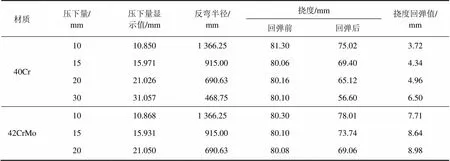
表2 基于试验所测得的回弹值

3 结果分析与讨论

3.1 中性层偏移对回弹的影响

二辊矫直过程中性层偏移会改变棒材截面应力−应变的状态，从而改变棒材内弯矩的计算，最终影响回弹和棒材的矫后直线度。40Cr和42CrMo的曲线如图9所示。

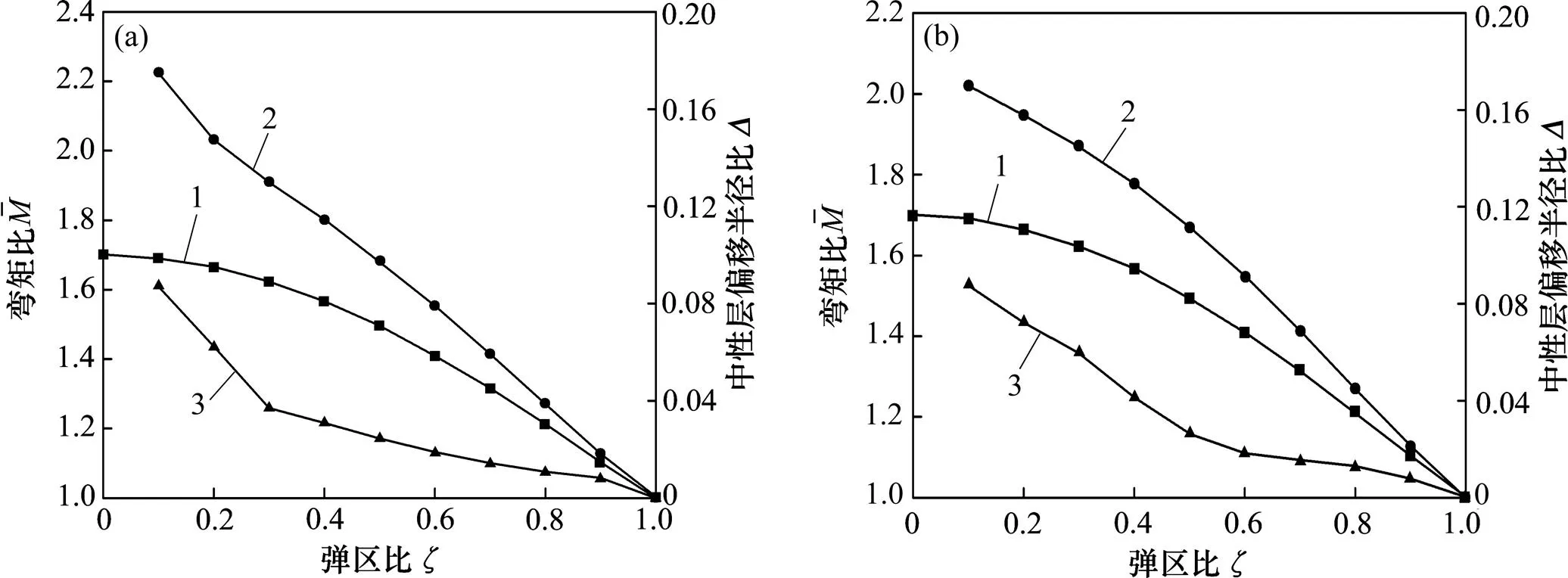
(a) 40Cr；(b) 42CrMo 1—Δ=0时曲线；2—Δ≠0时曲线；3—曲线。

(a) 40Cr；(b) 42CrMo 1—=0；2—≠0。

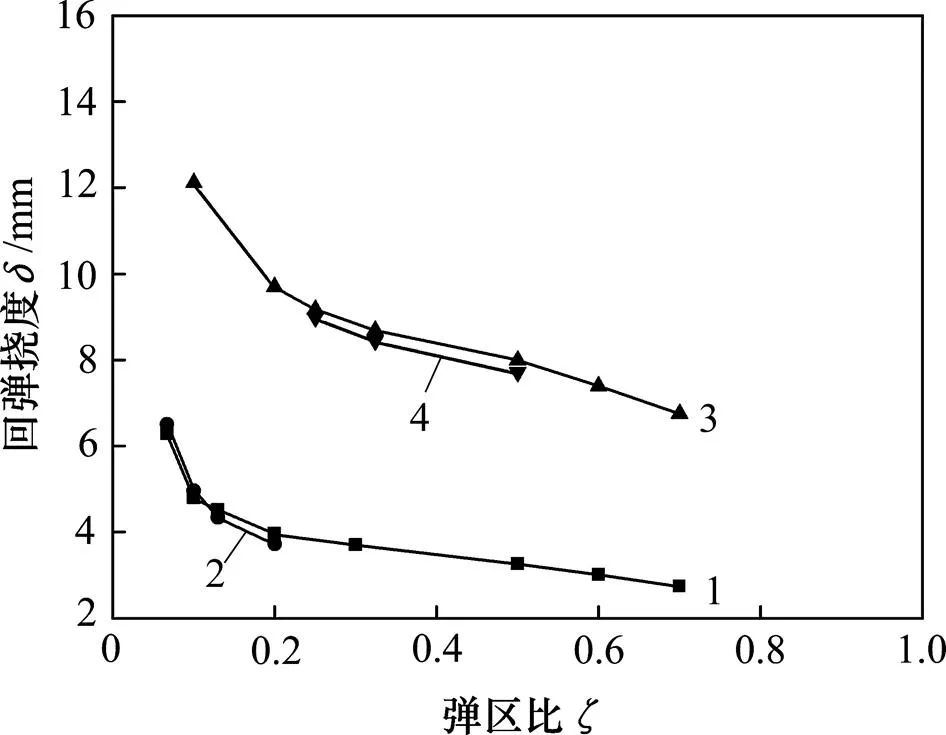
图10 回弹挠度与弹区比的关系

Fig. 10 Relationship between of deflection and elastic region value

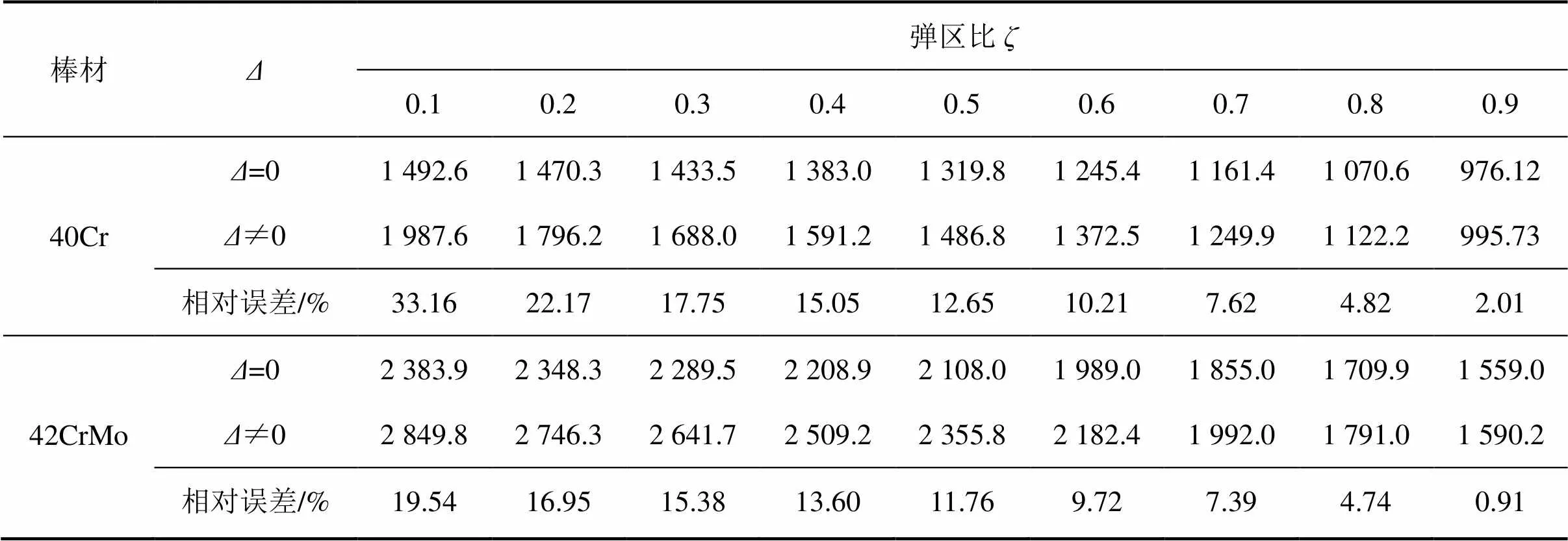
表3 中性层偏移对弯矩的影响

3.2 材料的力学性能对回弹的影响

实验所用的是材料分别是40Cr和42CrMo，它们的力学性能参数见表1，图12所示为2种棒材弯曲回弹后的形状。

(a) 40Cr；(b) 42CrMo

1—40Cr回弹理论值；2—40Cr回弹实验值；3—42CrMo回弹理论值；4—42CrMo回弹实验值。

图12所示为不同材料的挠度与弹区比关系曲线。从图12可知：在考虑材料硬化条件下，考虑中性层偏移的棒材矫直挠度回弹计算理论值与实验值基本一致。它们随着弹区比增大而减小，其中，42CrMo理论值与实验值的相对误差很小，在2.12%~3.63%范围内；而40Cr理论值与实验值相对误差为3.22%~ 6.45%，这主要是由于双线性拟合模型更接近42CrMo的应力−应变曲线，40Cr的应力−应变存在屈服平台，与42CrMo相比，其双线性硬化拟合精度较低。同时，从图12可以看出：42CrMo回弹挠度比40Cr棒材的大，这说明金属材料性能对回弹挠度影响较大。这是因为在相同的弹区比时，屈服强度高的42CrMo弯曲所需要的力矩大，最终卸载后回弹弯矩也大[25]，因此42CrMo棒材回弹挠度比40Cr的大。

3.3 曲率对回弹的影响

挠度与曲率关系曲线如图13所示。从图13可以看出：随着曲率的增大，棒材回弹挠度越大；这是因为曲率增大，反弯半径就越小，棒材弯曲程度愈大，进而回弹挠度增大。同时，2种材料的回弹挠度理论值与实验值基本一致，40Cr与42CrMo最大相对误差分别为6.45%和3.63%，低于不考虑中性层偏移时的31.65%和9.91%，表明式(30)计算精度较高。

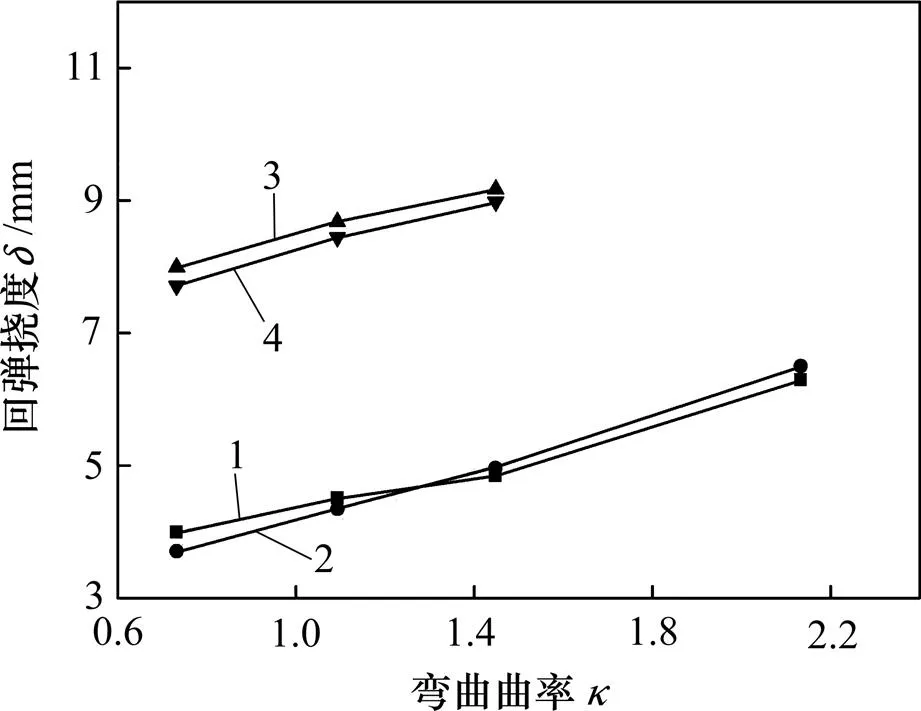
1—40Cr回弹理论值；2—40Cr回弹实验值；3—42CrMo回弹理论值；4—42CrMo回弹实验值。

4 结论

1) 建立了棒材矫直回弹挠度计算模型，可对高精度棒材二辊矫直过程中回弹挠度进行计算和分析。实验证明了该模型的正确性，对提高棒材矫直精度及完善其弯曲弹塑性变形理论提供了理论参考。

2) 基于二辊矫直变形特点和矫直理论，得到棒材矫直所需要的最大应变不超过5的结论，提出了在应变至5之间进行拟合的新双线性矫直拟合方法。与传统的拟合方法相比，40Cr与42CrMo的拟合校正决定系数由0.833 1和0.946 5提高到0.936 1和0.983 7，拟合精度分别提高了10.30%和3.72%。

3) 棒材回弹挠度不仅与矫直过程棒材受力状态、材料力学性能和曲率有关，还与棒材同矫直辊的接触位置有关。棒材回弹挠度随着中性层偏移值、材料屈服强度和曲率增大而增大。40Cr与42CrMo 2种棒材最大相对误差分别为6.45%和3.63%，低于不考虑中性层偏移和材料硬化时的31.65%和9.91%。

[1] 王云. 棒材二辊矫直过程及关键技术研究[D]. 秦皇岛: 燕山大学机械工程学院, 2013: 3−4.WANG Yu. Study on process and key technology of two-roll straightening[D]. Qinhuangdao: Yanshan University. School of Mechanical Engineering, 2013: 3−4.

[2] 崔甫. 矫直技术与理论的新探索[M]. 北京: 冶金工业出版社, 2010: 8−9.CUI Fu. The New Exploration of straightening technology and theory[M]. Beijing: Metallurgical Industry Press, 2010: 8−9.

[3] LI Heng, SHI Kaipeng, YANG He, et al. Springback law of thin-walled 6061-T4 Al-alloy tube upon bending[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(suppl 2): 357−363.

[4] 岳睿. 带状金属板材弯曲的回弹[J]. 塑性工程学报, 2009, 16(2): 29−33.YUE Rui. Study on the springback for narrow steel sheet[J]. Journal of Plasticity Engineering, 2009, 16(2): 29−32.

[5] 张冬娟, 崔振山, 李玉强, 等. 宽板大曲率半径纯弯曲回弹量理论分析[J]. 工程力学, 2006, 23(10): 77−81.ZHANG Dongjuan, CUI Zhenshan, LIYuqiang, et al. The springback of wide metal sheet after large radius pure bending[J]. Engineering Mechanics, 2006, 23(10): 77−81.

[6] GU R J, YANG H, ZHAN M, et al. Research on the springback of thin walled tube NC bending based on the numerical simulation of the whole process[J]. Computational Materials Science, 2008, 42(4): 537−549.

[7] ZHENG Q, AOYAMA T, SHIMIZU T, et al. Experimental and numerical analysis of springback behavior under elevated temperatures in micro bending assisted by resistance heating[J]. Procedia Engineering, 2014, 81: 1481−1486.

[8] 刘婧瑶, 唐承统, 宁汝新. 薄壁管纯弯曲塑性成形分析及回弹计算[J]. 塑性工程学报, 2009, 16(2): 5−9, 14.LIU Qianyao, TANG Chengtong, NING Ruxin. Plastic- formation analysis and springback calculating of thin-wall tube pure-bending[J]. Journal of Plasticity Engineering, 2009, 16(2): 5−9, 14.

[9] BURANATHITI T, CAO Jian. An effective analytical model for springback prediction in straight flanging process[J]. International Journal of Material and Product Technology, 2004, 21(1/2/3): 137−153.

[10] 贾美慧, 唐承统. 不锈钢管材弯曲成形回弹预测模型研究[J]. 北京理工大学学报, 2012, 32(9): 910−914.JIA Meihui, TANG Chengtong. Springback prediction model on tube bending formation of stainless steel[J]. Transactions of Beijing Institute of Technology, 2012, 32(9): 910−914.

[11] 张深, 吴建军. 空间弯管的回弹预测[J]. 航空学报, 2011, 32(5): 953−960.ZHANG Shen, WU Jianjun. Spring-back prediction of non- planar tube bending[J]. Acta Aeronauticaet Astronautic Sinica, 2011, 32(5): 953−959.

[12] ZHU Y X, LIU Y L, LI H P, et al. Springback prediction for rotary-draw bending of rectangular H96 tube based on isotropic, mixed and Yoshida-Uemori two-surface hardening models[J]. Materials and Design, 2013, 47: 200−209.

[13] 刘海燕, 金霞. 板料成形的回弹预测方法研究[J]. 机械制造与研究, 2008, 37(6): 40−44.LIU Haiyan, JIN Xia. Springback prediction method research of sheer metal forming[J]. Journal of Machine Design and Research, 2008, 37(6): 40−44.

[14] 潘昌平. 管材弯曲回弹及弯管机控制系统的研究[D]. 长春: 吉林大学机械科学与工程学院, 2008: 17−25.PAN Changping. Research on the bending spring-back of thin-walled tube and the control system of tube bending machine[D]. Changchun: Jilin University. College of Mechanical Science and Engineering, 2008: 17−25.

[15] 官英平, 张庆, 赵军. 中性层内移对弯曲回弹的影响[J]. 锻压技术, 2007, 32(2): 26−27.GUAN Yingping, ZHANG Qing, ZHAO Jun. Influence of neutral layer inside displacement on bending spring-back[J]. Forging & Stamping Technology, 2007,32(2): 26−27.

[16] 陈石保. 金属圆棒料弯曲回弹的探讨[J]. 锻压技术, 1991(4): 38−40.CHEN Shibao. The discussion on bending springback of metal bar[J]. Forging & Stamping Technology, 1991(4): 38−40.

[17] 俞汉清, 陈金德. 金属塑性成形原理[M]. 北京: 机械工业出版社, 1999: 121−122.YU Hanqing, CHEN Jinde. The principle of metal plastic forming[M]. Beijing: China Machine Press, 1999: 121−122.

[18] 张伟玮, 韩聪, 谢文才, 等. 管材弯曲回弹对内高压成形的影响及补偿方法[J]. 哈尔滨工业大学学报, 2014, 46(7): 36−39. ZHANG Weiwei, HAN Cong, XIE Wencai, et al. The effect of springback of CNC bending on hydro-formed sub-frame and compensation methods[J]. Journal of Harbin Institute of Technology, 2014, 46(7): 36−39.

[19] JOHNSON K L, 徐秉业, 罗学富. 接触力学[M]. 北京: 高等教育出版社, 1992: 51−58.JOHNSON K L, XU Bingye, LUO Xuefu. Contact mechanics[M]. Beijing: Higher Education Press, 1992: 51−58.

[20] 余同希, 章亮炽. 塑性弯曲理论及其应用[M]. 北京: 科学出版社, 1992: 43−44.YU Tongxi, ZHANG Liangzhi. Plastic bending theory and application[M]. Beijing: Science Press, 1992: 43−44.

[21] 肖景容, 姜奎华. 冲压工艺学[M]. 北京: 机械工业出版社, 2006: 116−117.XIAO Jingrong, JIANG Kuihua.The stamping technology[M].Beijing: Machinery Industry Press, 2006: 116−117.

[22] 赵军, 曹宏强, 展培培, 等. 纯弯曲过弯矫直等价原理及其试验验证[J]. 机械工程学报，2012, 48(8): 28−33.ZHAO Jun, CAO Hongqiang, ZHAN Peipei, et al. Pure bending equivalent principle for over-bend straightening and experimental verification[J]. Journal of Mechanical Engineering, 2012, 48(8): 28−33.

[23] 崔甫. 矫直原理与矫直机械[M]. 北京: 冶金工业出版社, 2007: 8−9.CUI Fu. Straightening principles and straightening machine[M]. Beijing: Metallurgical Industry Press, 2007: 8−9.

[24] 闫长林. Φ8~32 mm棒材矫直机结构参数及工艺参数研究[D]. 沈阳: 东北大学机械工程与自动化学院, 2010: 40−41.YAN Changlin. Research on structural parameters and process parameters of Φ8−32 mm bar straightening machine[D]. Shenyang: Northeastern University. School of Mechanical Engineering and Automation, 2010: 40−41.

[25] 李恒, 杨合, 宋飞飞, 等. 材料性能波动下TA18钛管绕弯回弹行为[J]. 稀有金属材料与工程, 2014, 43(1): 64−71. LI Heng, YANG He, SONG Feifei, et al. Springback rules of TA18 titanium tube upon rotary draw bending under variations of material properties[J]. Rare Metal Materials and Engineering, 2014, 43(1): 64−71.

Neutral layer offset rebound model based on elastic-plastic pressure

MA Ziyong1, MA Lifeng1, 2, HUANG Qingxue1, MA Lidong1, CHU Zhibing1, HUANG Zhiquan1

(1. Metallurgical Equipment Design Theory and Technology Key Laboratory of Shanxi Province, Taiyuan University of Science and Technology, Taiyuan 030024, China; 2. Superplasticity & Plasticity Institute, Jilin University, Changchun130000, China)

The location of stress neutral layer was determined considering the process characteristics of two-roll straightening and the neutral layer offset theory of elastic-plastic pressure. Considering the neutral layer offset and material hardening conditions, the new bilinear fitting method which was combined with two-roll straightening theory and stress-strain was proposed. On the basis of fitting method and neutral layer offset, the elastic-plastic deformation of element was analyzed, the formula of new moment ratio was given, and a new concept of neutral layer offset radius ratio was also put forward. Finally, the calculation model of bar straightening springback deflection combined with the pure bending springback theory was established, and then the influence of neutral layer offset rebound to accuracy of two-roll straightening was analyzed and verified by experiments. The results show that theoretical data ​​are in good agreement with experimental data; the maximum relative error is 6.45%, which is lower than 31.65% when the neutral layer offset is ignored. The validity of theoretical analysis and model is proved.

bar straightening; neutral layer offset radius ratio; springback model; experimental analysis

10.11817/j.issn.1672-7207.2016.09.016

TG386.3+1

A

1672−7207(2016)09−3020−11

2015−05−14；

2015−09−19

国家重点基础研究发展规划(973计划)项目(2012CB722800)：中国博士后科学基金资助项目(2012M520677)：国家自然科学基金资助项目(51105264，51404160)：山西省科技攻关项目(20130321010-03) (Project(2012CB722800) supported by the National Basic Research Development Program (973 Program) of China; Project(2012M520677) supported by the National Science Foundation for Post-doctoral Scientists of China; Projects(51105264, 51404160) supported by the National Natural Science Foundation of China; Project(20130321010-03) supported by the Ministry of Major Science & Technology of Shanxi Province)

马立峰，教授，从事轧钢工艺与设备研究；E-mail: malifengfqh@163.com

(编辑 赵俊)