基于双环法回转体测量机在线温度误差补偿

钟莹，刘佳，李杏华



基于双环法回转体测量机在线温度误差补偿

钟莹，刘佳，李杏华

(天津大学精密测试技术与仪器国家重点实验室，天津，300072)

为补偿回转体测量机的测量误差，深入分析测量机结构热变形误差的表现形式，在此基础上，建立热误差补偿数学模型。提出一种基于双环法的在线温度误差补偿技术，通过实物测量，实时获取参考基准的测量误差，通过计算得到测量架的平移和倾斜误差，对工件不同高度的外径和内径热误差进行实时补偿。实验结果表明：回转体测量机经过在线温度误差补偿后，测量的稳定性误差从110 μm下降到7 μm，显著提高了测量的稳定性。该方法可以满足回转体类零件对高可靠性和高精度测量的要求，提高回转体测量机在线测量精度和效益，为回转体测量机的在线温度误差补偿提供了一种新的技术途径。

回转体测量机；热误差补偿；双环法；平移；倾斜

回转体零件在各个行业中起着关键的作用[1]，被广泛应用于工业和国防等领域中，如炮弹、导弹、发动机、机床和车辆的零部件等。随着科学创新的日新月异，对回转体类零件的精度检测要求越来越高，尤其是军工产品的精度检测要求更为严格[1]。回转体测量机特别适合回转类零件的检测[2−3]，但其测量精度受温度影响很大，热误差补偿是保证其检测精度的关 键[4−6]。目前，国内外温度误差补偿技术可以分为2种[7−9]，一种方法是隔离热源或减少热源对测量精度的影响，这种方法成本较高，适合于恒温室中使用，不利于测量仪器的在线使用；另一种方法的基本原理是建立温度误差数学模型，设置温度采集节点，实时采集与测头偏移相关的信号，计算出测头的偏移量，该方法不足之处在于受外界因素影响大，气流、人员走动和机床运行等产生的不同温度梯度都在很大程度上降低了补偿模型的精度。对于回转体测量机而言，测量机尺寸链长，结构复杂，分析和计算测量机的结构热变形极为困难，特别是在生产现场，复杂的温度梯度使得仪器结构的内外温度不一致，难以准确给出测头与回转工作台轴线的相对位置随温度变化的数学模型。另外，复杂的补偿算法和多节点的温度采集系统，不仅增加了测量机的复杂性，而且增加了成本，降低了可靠性，不利于测量机的在线测量推广[10−12]。为此，本文作者提出一种基于双环法获取温度误差补偿数据的方法，通过建立温度误差模型得到相应的平移和偏转量[13−14]，通过实物测量实现测量机的在线温度误差补偿，实时补偿由回转体测量机和被测工件热变形而产生的测量误差，为在线温度误差补偿提供一种新的技术途径。

1 回转体测量机设计

回转体测量机如图 1 所示，由外侧轴向测量架A、内测量架B、外侧径向测量架C、回转工作台D和基座E 5部分组成[14−15]。回转体工件通过螺纹套筒和夹头安装在回转工作台上，测量时回转工作台带动工件连续转动，测头测得某个截面各个点的坐标，得到各个圆柱面的尺寸、位置和形状误差。本项目设计只针对回转体内、外径测量，因此着重介绍内径测量架B和外侧径向测量架C。

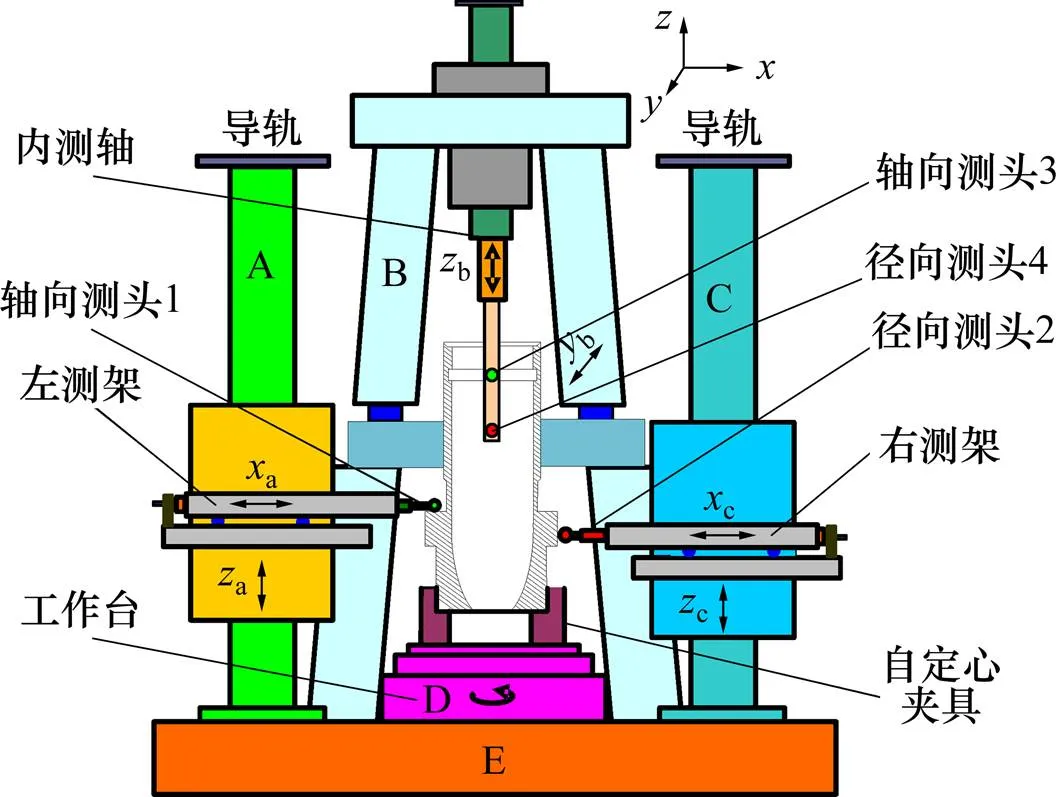
图1 回转体测量机结构

工件内表面测量架B在如图1所示的−平面内运动，使电感侧头的球头与被测工件表面的法线方向一致。被测工件安装在回转工作台上，被测件随工作台做回转运动，内测架B的基座可沿导轨做向运动，内测主轴做向运动，测头通过内侧杆安装在主轴上，随基座的向运动和主轴的向运动使测头接触到工件的被测点，被测工件转动1周，测量1个参数。

在回转体零件测量中，测量机包含B，C，D 3个运动部件，共设4个坐标系，分别为内测量架B的坐标系(b,b,b)，外测量架C的坐标系(c,c,c)，回转工作台的坐标系(,,)，机器坐标系(,,)。

如图1所示，回转体零件安装在回转工作台D的基面E上，基面E即为机器坐标系=0的平面，测量时工件转动，此时的回转中心即为=0，=0的坐标原点。内径测量架B的运动方向为b，外径测量架C的运动方向为c，每测量1个点即可得到该点的坐标(,,)或者(,,)，其中为回转工作台的转角。

2 双环法温度误差补偿原理

2.1 热变形误差补偿的数学模型

热误差来源有测量机的结构热变形、测头的温度漂移和工件的热变形等，而测量机的结构热变形是主要的误差来源。因此，校准测量轴和回转体轴线的相对位置是补偿热变形误差的关键[13−15]。

假设在回转体测量的短时间中，测量机短期热变形误差可以忽略，由此建立了温度误差补偿的基本模型，如图2所示，其中，为测量架轴线相对于基准的平移量，为测头相对于回转轴线的偏转角，从而可以得到时刻热变形误差的补偿公式为

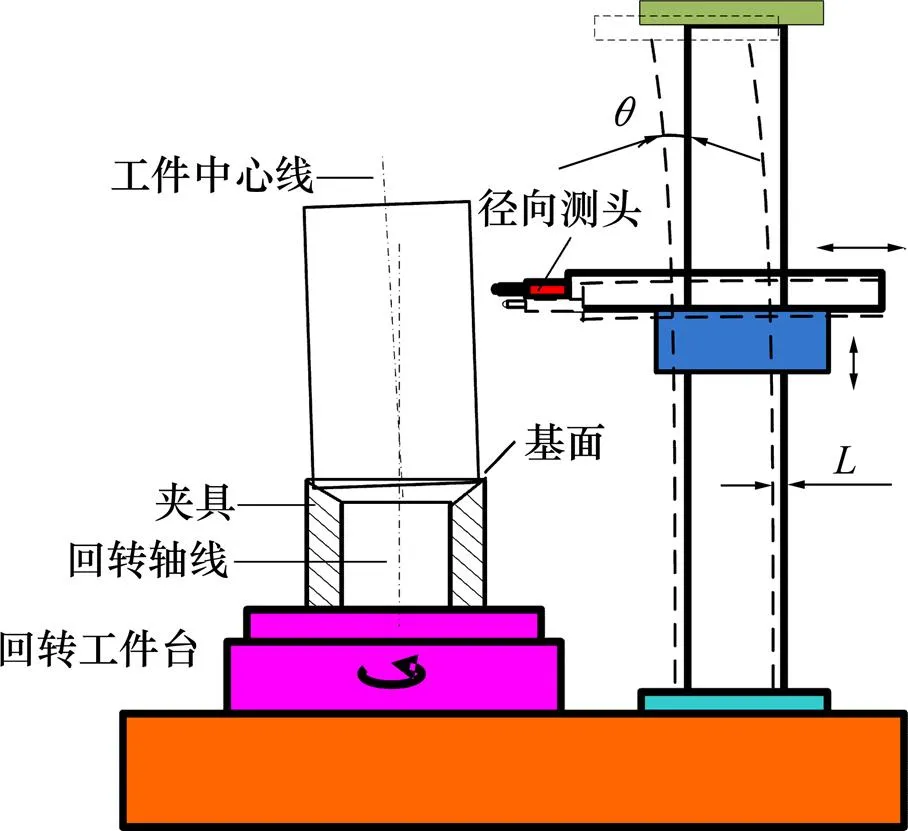
图2 测量机结构热变形图

对于工件形位误差(如同轴度等)，由于温度引起测量架相对于回转轴线的热变形(平移、偏转)不影响工件中心线的测量，故对形位公差不需要补偿。利用最小二乘法拟合，对工件进行中心线测量，

式中：(,)为测量某截面圆的圆心坐标；为该截面圆半径，截面圆上的点坐标(x,y)为

2.2 双环法误差补偿数据的获取

双环法误差补偿模型如图3所示。这类工件具有延伸公差，套筒a用于辅助测量工件延伸区的跳动，夹具b用于固定工件。针对此类工件的温度误差补偿，采用双环法，将套筒a和夹具b设计成基准件。作为基准，a和b的内、外径通过标定是已知的。同时为了消除基准件a和b的热变形误差对测量结果的影响，套筒a和夹具b的热膨胀系数要与待测工件一致。由于被测工件的热变形误差与基准a和b的热变形误差保持一致，因此该方法还可以有效补偿基准件a和b热变形产生的测量误差。

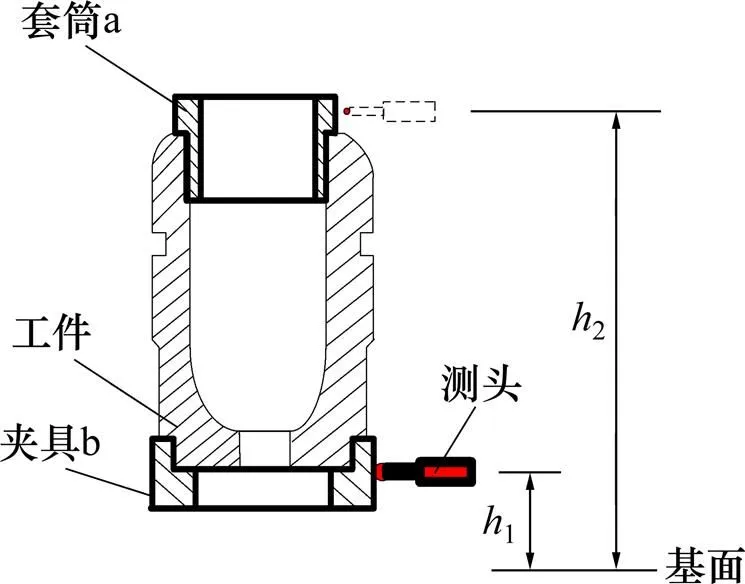
图3 双环法误差补偿模型

2.2.1 双环法外径误差补偿模型

图4所示为双环法在线温度误差外径补偿模型。首先测量基准件a的外径1，通过式(1)可以计算获得测量所得的外径和标定值之差：

式中：1为基准件a的高度。

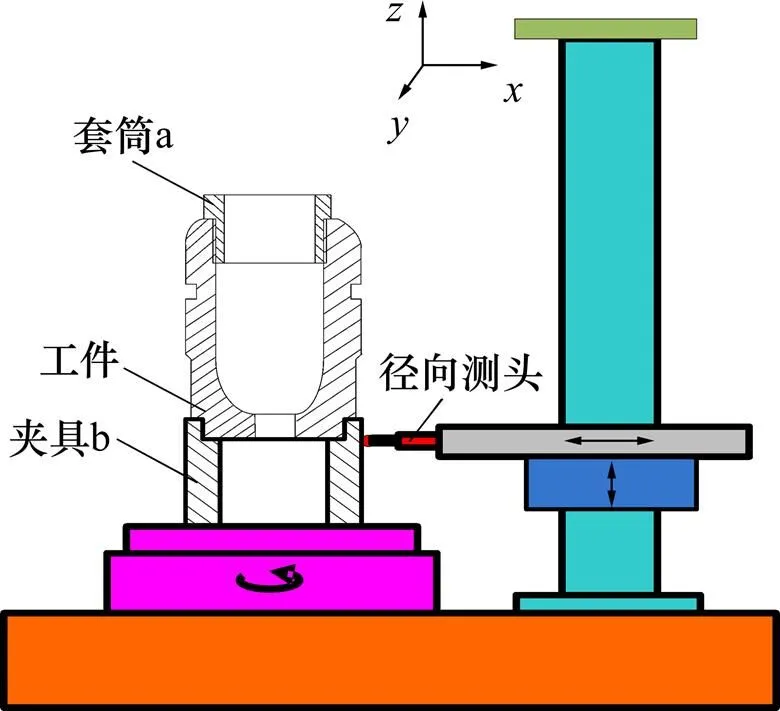
图4 双环法在线温度误差外径补偿模型

式中：2为基准件b的高度。

根据式(4)和式(5)可以得到测头相对于回转轴线的偏移量为

根据式(6)和(7)，可以得到任意高度的外径温度误差补偿公式：

其中：h为工件外表面任意截面的高度。

2.2.2 双环法内径误差补偿模型

双环法温度误差内径补偿模型如图5所示。首先测量基准件a的内径1，通过式(1)可以计算获得测量所得的内径和标定值之差：

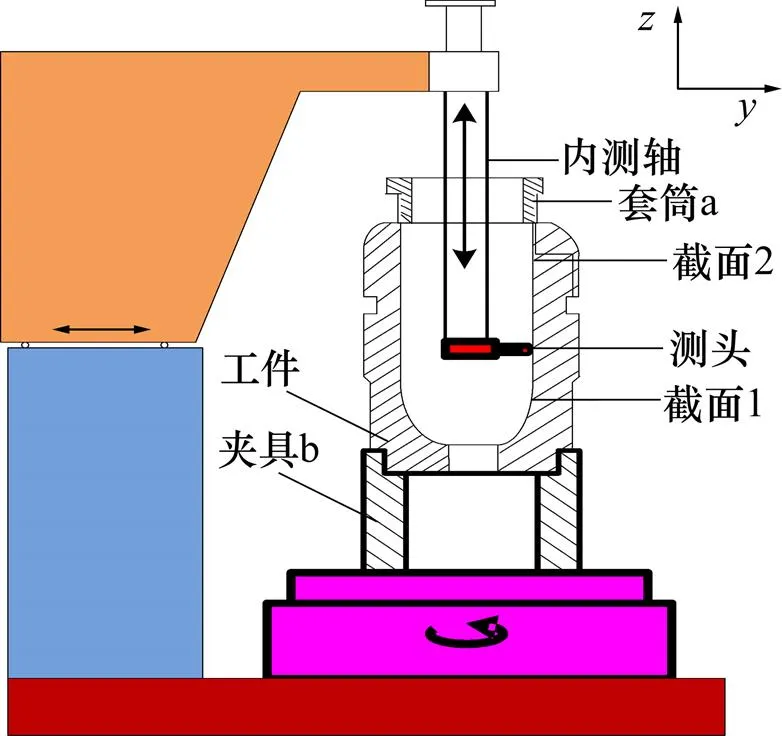
图5 双环法在线温度误差内径补偿模型

式中：2为测量夹具b时测头的高度。

根据式(9)和式(10)可以得到，内测量架相对于回转轴线的偏移量为

根据式(11)和(12)可以得到内测量架测量回转体内径时，任意截面的温度产生的误差为

式中：z为回转体工件内径任意截面的高度。

根据式(8)和(13)可以对测量机在各个高度的外径和内径误差进行实时补偿和修正，并建立完善的测量机在线温度误差补偿模型，以补偿回转体测量机由于热变形产生的测量误差。

3 测量结果和误差分析

针对安装套筒的回转体工件，通过双环法获取实时温度误差补偿数据，采用高400 mm，最大外径为125 mm的混凝土攻坚弹M125作为被测工件。

在实验室对M125进行连续测量，得到1组内径和外径误差补偿数据，通过式(8)和式(13)可以得到内外径补偿后的测量数据。

在温度可控的恒温实验室条件下，通过测量可知，补偿前后的测量数据稳定性误差(由于被测工件存在加工误差，通过测量数据最大值与最小值之差来评定测量数据的稳定性)均保持在7 μm以内。

为了进一步验证回转体测量机测量精度受温度变化的影响，在开放实验室条件下，连续测量M125型号炮弹1周，测量时其他条件相同。125 mm外径和94 mm内径的测量数据如表1所示。由表1可知：未经补偿的外径和内径稳定性误差分别可达113 μm和102 μm，经过补偿后数据稳定性误差分别为6 μm 和7 μm。通过外径和内径实验测量数据补偿前后对比可知：双环法补偿模型有效地补偿了测量机的热变形误差。

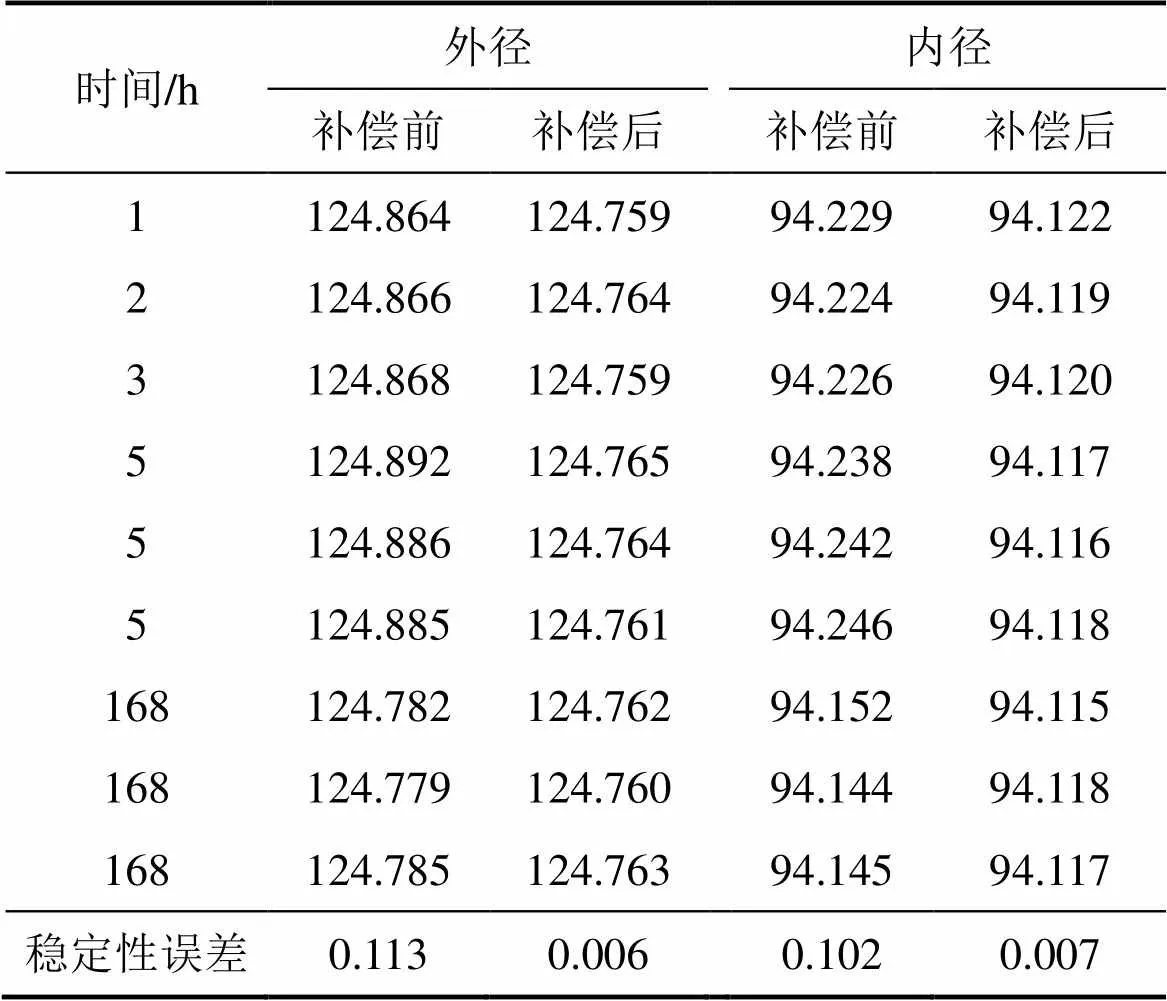
表1 外径和内径连续测量实验结果

4 结论

1) 提出了通过实物测量实现温度误差补偿的新思路与方法，为在线温度误差补偿提供一种新的技术途径。

2) 建立基于双环法的温度误差补偿模型。由于参考基准与被测工件的热变形相同，该模型可以自动补偿被测工件产生的热变形误差。

3) 通过计算得出不同温度条件下测量机的平移量和偏转角，进而对内径和外径温度误差进行实时补偿。经过补偿后外径和内径测量数据的稳定性分别提高了107 μm和95 μm，误差均保持在7 μm以内，可以满足工业测量中对精度和稳定性的要求。

[1] 顾强, 张亚, 路国英, 等. 弹体外形尺寸自动检测系统[J]. 弹箭与制导学报, 2008, 28(4): 146−148. GU Qiang, ZHANG Ya, LU Guoying, et al. Automatic checkout system of projectile body dimensions[J]. Journal of Missiles and Guidance, 2008, 28(4): 146−148.

[2] 张国雄. 三坐标测量机的发展趋势[J]. 中国机械工程, 2000, 11(1): 222−226. ZHANG Guoxiong. Trends of coordinate measuring machine[J]. China Mechanical Engineering, 2000, 11(1): 222−226.

[3] 赵则祥, 路明, 李学新, 等. 基于新一代几何产品技术规范的圆柱体直径的测量方法研究[J]. 中国机械工程, 2006, 17(11): 1179−1182. ZHAO Zexiang, LU Ming, LI Xuexin, et al. Measurement method of cylinder diameters based on new generation geometrical product specifications[J]. China Mechanical Engineering, 2006, 17(11): 1179−1182.

[4] ZHANG G X, GUO J B, LIU S G, et al. The development of cylindrical coordinate measuring machines[J]. Measurement Science and Technology, 2010, 21(5): 54003−54009.

[5] WANG W, ZHANG Y, YANG J, et al. Geometric and thermal error compensation for CNC milling machines based on Newton interpolation method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013, 227(4): 771−778.

[6] 王维, 杨建国, 姚晓栋, 等. 数控机床几何误差与热误差综合建模及其实时补偿[J]. 机械工程学报, 2012, 48(7): 165−170. WANG Wei, YANG Jianguo, YAO Xiaodong, et al. Synthesis modeling and real-time compensation of geometric error and thermal error for CNC machine tools[J]. Journal of Mechanical Engineering, 2012, 48(7): 165−170.

[7] 李醒飞, 董成军, 陈诚, 等. 单热源作用下滚珠丝杠的温度场建模与热误差预测[J]. 光学精密工程, 2012, 20(2): 337−343. LI Xingfei, DONG Chengjun, CHEN Cheng, et al. Temperature model of ball screw and thermal error prediction under single heat[J].Optics and Precision Engineering, 2012, 20(2): 337−343.

[8] MIAO E M, GONG Y Y, NIU P C, et al. Robustness of thermal error compensation modeling models of CNC machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(9/10/11/12): 2593−2603.

[9] 王时龙, 杨勇, 周杰, 等. 大型数控滚齿机热误差补偿建模[J]. 中南大学学报(自然科学版), 2011, 42(10): 3066−3072. WANG Shilong, YANG Yong, ZHOU Jie, et al. Modeling of thermal error compensation of large-scale numerical control gear hobbing machine[J]. Journal of Central South University (Science and Technology), 2011, 42(10): 3066−3072.

[10] JAKSTAS A, KAUSINIS S, BARAUSKAS R, et al., Thermal error analysis in precision length measurements[J]. Measurement, 2014, 51(1): 133−146.

[11] SARHAN A A D. Investigate the spindle errors motions from thermal change for high-precision CNC machining capability[J]. International Journal of Advanced Manufacturing Technology, 2014, 70(5/6/7/8): 957−963.

[12] LI Y, ZHAO W, WU W, et al. Thermal error modeling of the spindle based on multiple variables for the precision machine tool[J]. International Journal of Advanced Manufacturing Technology, 2014, 72(9/10/11/12): 1415−1427.

[13] 李杏华, 洪燕. 回转体测量机的双向法在线温度误差补偿[J]. 光电工程, 2013, 40(1): 94−99. LI Xinghua, HONG Yan. The method of online thermal error compensation based on the bidirectional measurement of revolving body measuring machines[J]. Opto-Electronic Engineering, 2013, 40(1): 94−99.

[14] ZHANG G X, ZHANG H Y, GUO J B, et al. Error compensation of cylindrical coordinate measuring machines[J]. CIRP Annals: Manufacturing Technology, 2010, 59(1): 501−504.

[15] 李文静. 七轴测量机数据处理及专用软件设计研究[D]. 天津: 天津大学精密仪器与光电子工程学院, 2009: 15−26. LI Wenjing. Research on data processing and dedicated software design for seven-axial measuring machine[D]. ​​Tianjin: Tianjin University. School of Precision Instrument and Opto-electronics Engineering, 2009: 15−26.

Online thermal error compensation of rotatory measuring machines based on bicyclic law

ZHONG Ying, LIU Jia, LI Xinghua

(State Key Laboratory of Precision Measurement Technology and Instruments, Tianjin University, Tianjin 300072, China)

In order to compensate thermal error for rotatory measuring machine, the measuring machine’s structure manifestation of thermal deformation error was analyzed, on this basis of which the mathematical model of thermal error compensation was established. The method was proposed based on bicyclic law of online temperature error compensation technology. Through in-kind measurement, workpieces’ offset and tilt errors were calculated by achieving real-time measurement error of reference benchmark to compensate thermal errors of different heights of workpieces of both outside and inside diameters in real time. The results show that the error of the measuring stability error is reduced from 110 μm to 7 μm after compensation, improving measuring stability significantly. The compensation method can satisfy the need of rotating parts for high reliability and precision measurement, improving rotatory measuring machine’s online measurement accuracy and efficiency, as well as providing new method of compensating thermal error for rotatory measuring machines.

rotatory measuring machine; thermal error compensation; bicyclic law; offset; tilt

10.11817/j.issn.1672-7207.2016.09.012

TH161.4；TH711

A

1672−7207(2016)09−2992−05

2015−06−11；

2015−10−11

国家自然科学基金资助项目(51105272) (Project(51105272) supported by the National Natural Science Foundation of China)

李杏华，博士，副教授，硕士生导师，从事大尺寸精密测试技术和测试信息处理技术研究；E-mail: li.xinghua@126.com

(编辑 赵俊)