微注射成型超声塑化中黏弹性生热效应

贾云龙，蒋炳炎，彭华建，张胜，刘小超



微注射成型超声塑化中黏弹性生热效应

贾云龙，蒋炳炎，彭华建，张胜，刘小超

(中南大学高性能复杂制造国家重点实验室，湖南长沙，410083)

考虑超声衰减，基于广义Maxwell力学模型建立超声塑化聚合物黏弹性生热数学模型，通过数值计算研究聚甲基丙烯酸甲酯(PMMA)黏弹性生热规律和生热过程温度场分布，结合超声塑化PMMA形态演变实验分析黏弹性生热效应在聚合物由玻璃态到黏流态转变中的作用。研究结果表明：聚合物的温度是影响黏弹性生热的重要因素，PMMA的黏弹性生热效应在105~150 ℃之间作用明显；塑化样品由玻璃态到黏流态的转变过程温度场分布不均，靠近工具头端面和塑化腔壁处先于其他部分达到黏流温度；超声作用初始阶段摩擦生热作用明显，颗粒界面消失后黏弹性生热起主要作用。

微注射成型；超声塑化；广义Maxwell模型；黏弹性生热效应

微注射成型是毫克级微塑件主要成型方法之 一[1]。目前常规微注射成型机多采用螺杆塑化方式，螺杆直径在制造上存在最小直径限制，因而塑化量也存在最小极限。毫克级的微塑件需要的一次塑化量很小，采用常规微型注塑机成型时需设计较大流道，存在材料浪费问题，对于大批量生产的注射成型不容忽视[2]。微注射成型超声塑化是一种新型塑化方式，具有节能、高效的优点可以解决常规注塑机最小塑化量受限制问题[3−5]。微注射成型超声塑化量小，时间短，能量集中，塑化质量对超声参数较为敏感，参数不合理时容易出现烧焦和塑化不均现象。为获得良好的塑化质量控制方法，有必要对超声塑化生热机理进行研究。目前学者主要利采用实验方法研究超声参数的影响[2, 6−9]，对超声塑化生热过程机理未形成统一认识。MICHAELI等[7]提出超声塑化生热效应包含塑料颗粒界面摩擦生热和塑料内部黏弹性生热，但研究以超声参数对制件质量影响实验为主，未对塑化过程生热机理深入探讨；JIANG等[8]从理论角度分析了超声空化效应对塑化作用的影响，但前提是聚合物已处在黏流态温度之上，玻璃态到黏流态之间的生热机理没有涉及。刘小超[10]仿真研究了超声作用下聚合物由玻璃态到黏流态转化过程中的黏弹性生热效应，但没有考虑温度对聚合物黏弹性生热率的影响。本文作者针对超声塑化过程中的黏弹性生热效应进行研究，选择典型的热塑性聚合物聚甲基丙烯酸甲酯(PMMA)为研究对象，考虑温度对聚合物黏弹生热的影响，采用广义Maxwell力学模型建立超声塑化黏弹性生热模型，数值计算研究黏弹性生热规律及生热过程温度场分布，结合聚合物颗粒塑化形态演变实验分析黏弹性生热在聚合物由玻璃态到黏流态转变中的作用。

1 超声塑化过程中的生热效应

微注射超声塑化示意图如图 1所示，聚合物原料一般为颗粒状，为超声工具头端面振幅，为塑化压力，塑化腔内聚合物颗粒在工具头高频振动下塑化。塑化过程包括聚合物从玻璃态转变到黏流态的融化过程及获得良好流动性。聚合物处于不同状态时超声作用不同，聚合物由玻璃态到黏流态转变过程存在2种主要生热效应，即颗粒间及腔壁处的摩擦生热和聚合物在工具头高频载荷作用下内部黏弹性生热。黏流态之后超声的作用主要是改善溶体流动性，本文暂不涉及。

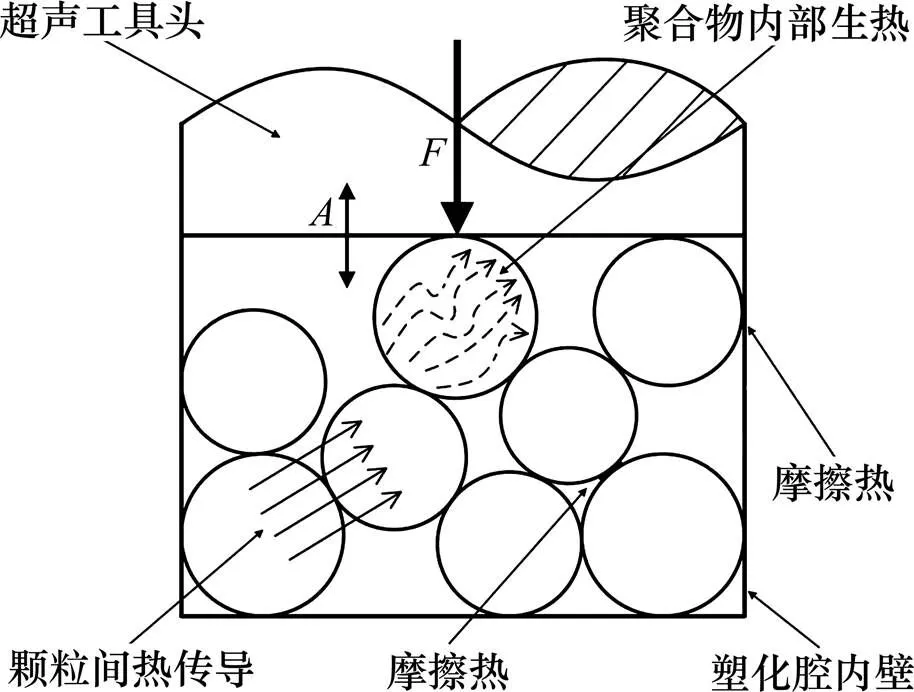
图1 超声塑化过程生热效应示意图

2 超声塑化黏弹性生热模型

2.1 超声塑化黏弹性生热物理模型

为便于研究，不考虑颗粒间摩擦生热效应，假设塑化聚合物内部没有瑕疵，介质分布均匀。模型为圆柱形，直径×高度为10 mm×5 mm。如图2所示，聚合物承受超声工具头作用的正弦交变压力载荷。由于聚合物的黏弹特性，应变滞后应力，工具头所做的功一部分转化为热量，这是黏弹性生热的物理实质。

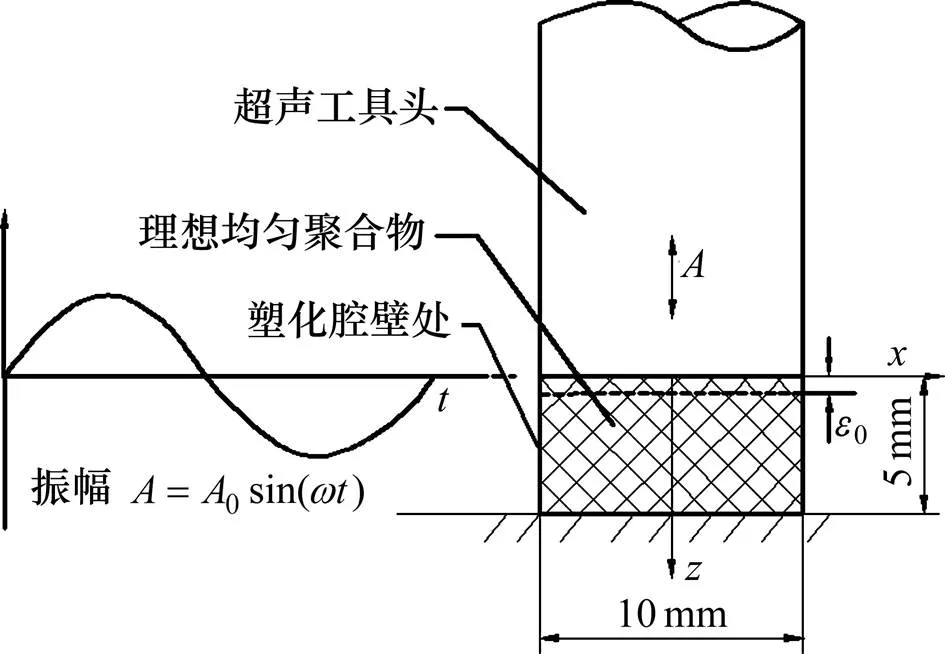
图2 超声塑化过程中黏弹性生热简化模型

2.2 超声塑化黏弹性生热数学模型

聚合物在超声频率载荷作用下加压和卸载曲线不重合(图3)，形成“滞后圈”，其面积就是单作用周期内工具头克服链段内摩擦所做的功，于是可得超声作用1 s时间内单位体积聚合物的黏弹性生热量：

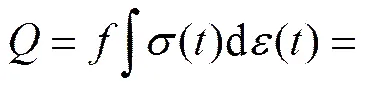
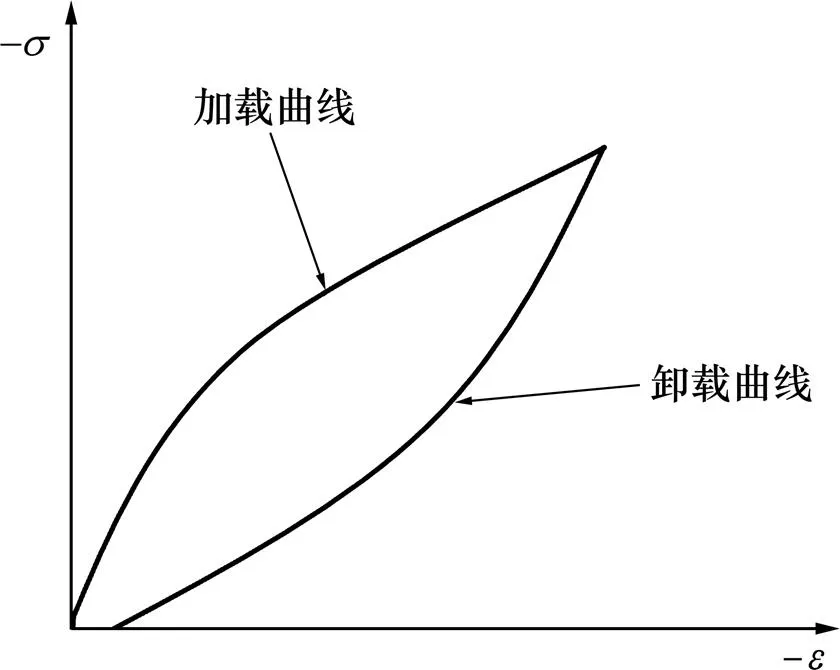
图3 一个周期内聚合物应力−应变曲线

式中：为工具头振动频率；为时间；和分别为应力应变幅值；为应变滞后角；为工具头振动角频率。

为研究方便，将应力应变表示为复数形式，则聚合物的动态模量为

由式(2)可将变换为

即为黏弹性生热率，可见黏弹性生热与超声作用频率、振动幅值和聚合物在对应频率载荷下的损耗模量有关。

超声波在黏弹性物质中在传播时，传播方向上存在显著振幅衰减。聚合物在玻璃化转换温度以上黏弹特性明显，内部某处的振动幅值与应变幅值是线性关系，因此必须考虑超声在聚合物中传播方向上时的振幅衰减。超声工具头传播到在聚合物中的波动方程解为[11]

其中：为振动幅值；为声波的传播速度；为声波传播方向上至工具头距离；为声波传播的衰减因子，计算公式由文献[11]给出：

由式(3)~(5)可得考虑超声衰减作用时的黏弹性生热率的数学表达式为

2.3 高频载荷下聚合物的复数模量

聚合物模量同时与温度和载荷频率有关，低频载荷作用下的聚合物损耗模量曲线可通过DMA实验测得，然而高频下的损耗模量需通过时温等效原理外推获得[12]。为获得聚合物损耗模量数学表达式，采用广义Maxwell力学模型表征聚合物复数模量与温度和频率的关系：

式中：为广义Maxwell阶数序号；E和分别为对应各阶Maxell单元的静态松弛模量和松弛时间，为温度的函数。

不同温度下的松弛时间计算公式由Arrhenius方程[13]和半经验WLF方程分别给出：

式中：s为参考温度；为聚合物温度；g为聚合物的玻璃化转换温度；为聚合物松弛转变活化能；为气体摩尔常数；1和2为常数。

由式(6)~(8)可得不同位置处聚合物黏弹生热率关于频率和温度的数学表达式为

3 黏弹性生热数值计算与讨论

3.1 黏弹性生热数值计算策略

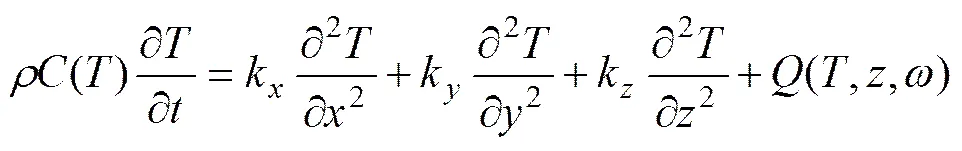
以典型的热塑性无定形聚合物聚甲基丙烯酸甲酯(PMMA)为研究对象，材料属性取Mitsubishi Rayon公司生产的ACRYPET TF−9型 PMMA，数据由Autodesk Moldflow 材料实验室提供，玻璃化转换温度为105 ℃，黏流化转换温度为160 ℃。文献[14]给出了PMMA在参考温度为玻璃化转换温度时广义Maxwell力学模型表示的各阶松弛模量和松弛时间，PMMA的松弛转变活化能取335 kJ/mol，WLF方程常数取1=17.6，2=65.5[15]，由式(10)可得给定超声频率和应变幅值时PMMA的黏弹性生热率。

采用商业软件ANSYS热分析模块求解控制方程(10)，选择三维热分析单元SOLID90，建立直径×高度为10 mm×5 mm的网格模型，在ANSYS中定义给定频率下的黏弹性生热率为节点温度和节点坐标的函数，设置较小步长(取0.01s)进行瞬态热分析，提取每一子步计算结束时单元节点温度，可获得控制方程(10)温度随时间变化的数值解。取工具头端面处振幅为40 µm，设置不同初始温度，研究温度对黏弹性生热的影响；取常见功率超声发生器频率15，20，25和30 kHz，分别计算上述频率下的，研究频率对黏弹性生热的影响；取超声频率为20 kHz，设置不同工具头处振幅，研究振幅对黏弹性生热的影响。

3.2 温度对PMMA黏弹性生热的影响

图4所示为工具头端面处节点的黏弹性生热曲线(超声频率为20 kHz)，结果表明，温度是影响PMMA的黏弹性生热的重要因素。初始温度过低时，升温速率较低，初始温度为95 ℃和97 ℃时在5 s内温升缓慢，温升分别为1.5 ℃和4.1 ℃；初始温度为99 ℃时在3.3 s前温升缓慢，随后升温速率急剧增加，温度在很短时间内升高到150 ℃；初始温度为100 ℃和102 ℃时升温趋势和99 ℃时一致，升温速率急剧上升时对应的时刻分别为2.4 s和1.1 s；105 ℃时(PMMA的玻璃化转换温度)黏弹性温升直接进入急剧上升阶段。然而温升至155 ℃左右后温升曲线逐渐趋于平缓，这表明PMMA黏弹性生热在高于其玻璃化转化温度约 50 ℃以上的温度区间比较明显，此温度范围内升温速率较大。TOLUNAY等[16]对超声焊接热塑性塑料生热的实验研究指出，超声载荷作用下塑料内部温度达到聚合物玻璃化转换温度时在一定范围内温升速率大幅增加，之后趋于平缓，与本文数值计算结果基本相符，这证明了本文建立的超声塑化黏弹性数值计算模型是正确的。

3.6.1 腹水。肝硬化腹水是肝硬化最常见的并发症，是肝功能减退和门静脉高压的共同结果。代偿期肝硬化患者10年内并发腹水约占60%，首发腹水后2年和5年病死率分别是50%和80%，大量腹水时可见腹部隆起，状如蛙腹，可发生脐疝，横膈抬高可引起呼吸困难，心悸，严重影响患者的生活质量[15]。

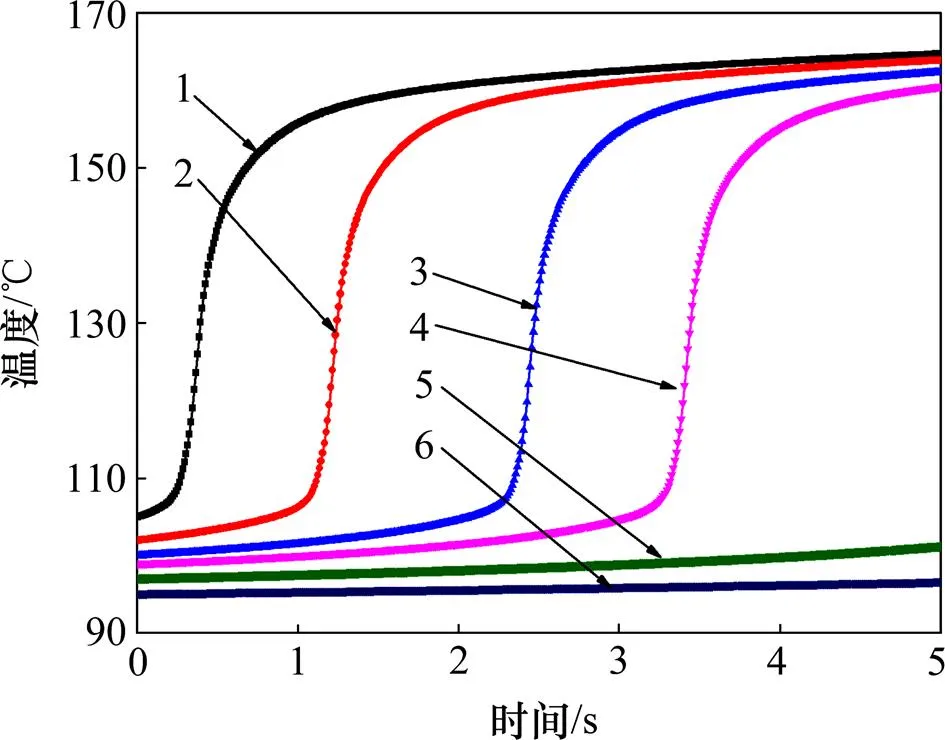
初始温度/℃：1—105；2—102；3—100；4—99；5—97；6—95。

从高分子链段运动角度分析，PMMA处在玻璃态时，超声频率载荷作用下的形变以分子内部键长键角的改变及侧基的运动为主，速度很快，力学响应以弹性为主，应变滞后应力现象不明显，损耗模量小；温度高于105 ℃时，PMMA进入玻璃态向高弹态转变温度区，PMMA性质发生很大变化，大分子链段开始运动，但受到的摩擦阻力较大，形变显著落后于应力变化，黏弹特性明显，损耗模量较大；温度进一步升高接近至黏流温度时分子链段运动又较为自由，损耗模量减小。故未融化前聚合物的黏弹性生热效应主要存在于其玻璃化转换温度以上的一段温度范围。超声作用时初始温度多在室温范围，低于大多数聚合物的玻璃化转换温度，因此黏弹性生热需要一定的激活热量使聚合物温度升高到玻璃化转变温度后才有显著作用，这也表明超声塑化初始阶段黏弹性生热不是主要生热效应，超声工具头作用下聚合物颗粒间及塑化腔壁处的剧烈摩擦生热应是提供黏弹性生热激活热量的主要来源。塑化原料的颗粒粒径和形状对摩擦生热影响较大，合适粒径和形状的颗粒有助于聚合物进入黏弹性生热快速升温阶段。

3.3 超声频率对黏弹性生热的影响

不同超声频率下PMMA黏弹性生热率随温度变化的曲线如图5所示。黏弹生热率在不同超声频率下随温度变化的趋势是一致的，取值较大的温度区间皆为100~150 ℃，最大值皆出现在PMMA玻璃化转换温度以上约20 ℃(125 ℃)附近，且处在同一数量级，但最大值相差较大。频率越高，黏弹性生热率越大，30 kHz时最大值约为15 kHz时的2倍。

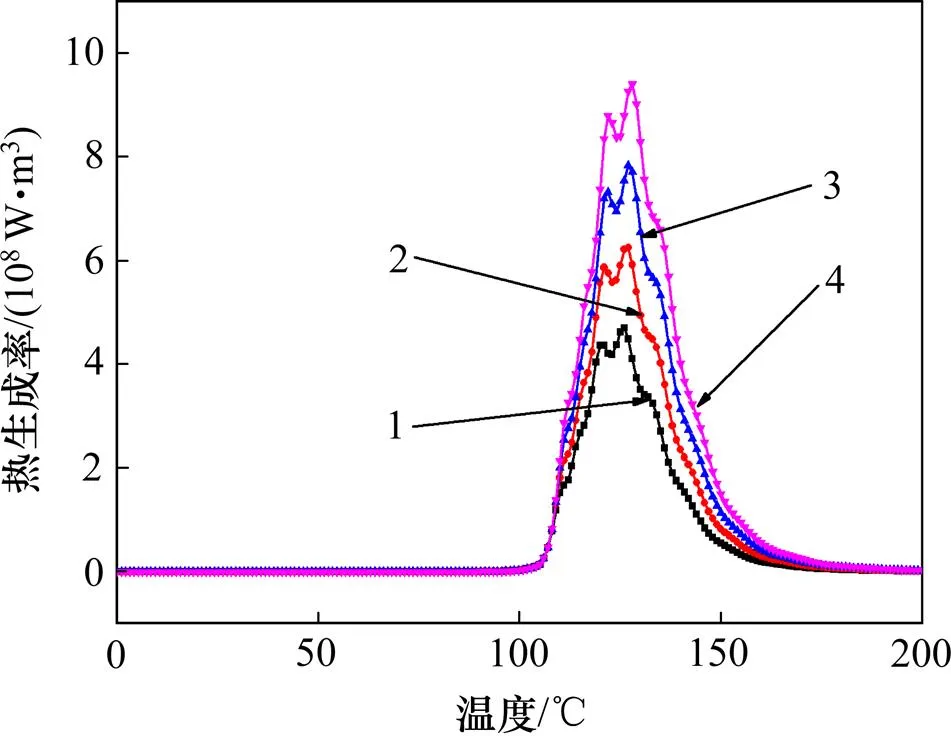
超声频率/kHz：1—15；2—20；3—25；4—30。

图6所示为不同频率下工具头端面处的黏弹性生热曲线。由图6可知：超声频率对PMMA的黏弹性生热过程影响较小。不同频率下黏弹性温升历程在100~110 ℃基本一致；110 ℃以后略有差异，频率越高，升温速度越快，但皆在很短时间内升高到150 ℃；155 ℃后升温皆趋于平缓，5 s结束时30 kHz作用下的温升仅较15 kHz作用下的温升高5.5 ℃。可见超声频率虽对黏弹性生热率影响较大，但常见功率超声频率范围内单纯提高频率对加快黏弹性生热过程意义不大。

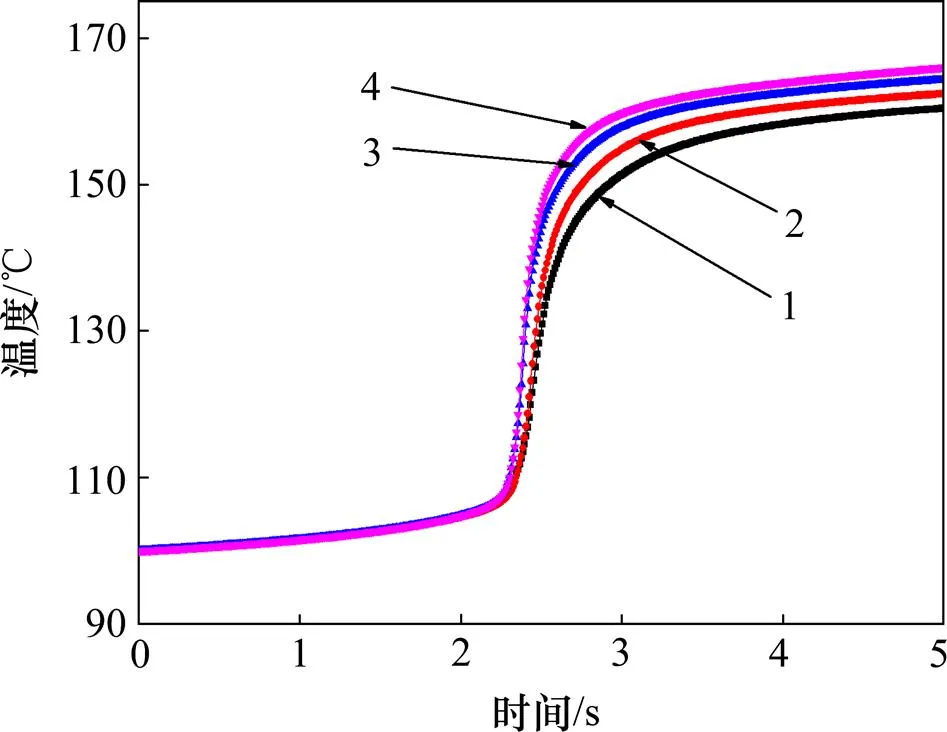
超声频率/kHz：1—15；2—20；3—25；4—30。

3.4 超声振幅对黏弹性生热的影响

由式(9)可知：聚合物黏弹性生热率正比于应变幅值的平方，超声振幅对黏弹性生热有较大影响。图7所示为工具头端面处PMMA在不同振幅下的温升曲线。可见：振幅为10 µm时黏弹性温升不明显，幅度为1.45 ℃，6 s后仍未达到玻璃化转换温度。振幅为20 µm以上时，温度达到玻璃化转换温度后急剧上升的趋势是一致的，但振幅越大，升温速率越快，对应的快速升温范围也有所增加。振幅50 µm时对应的快速升温范围为105~165 ℃，而20 µm时为105~ 150 ℃。

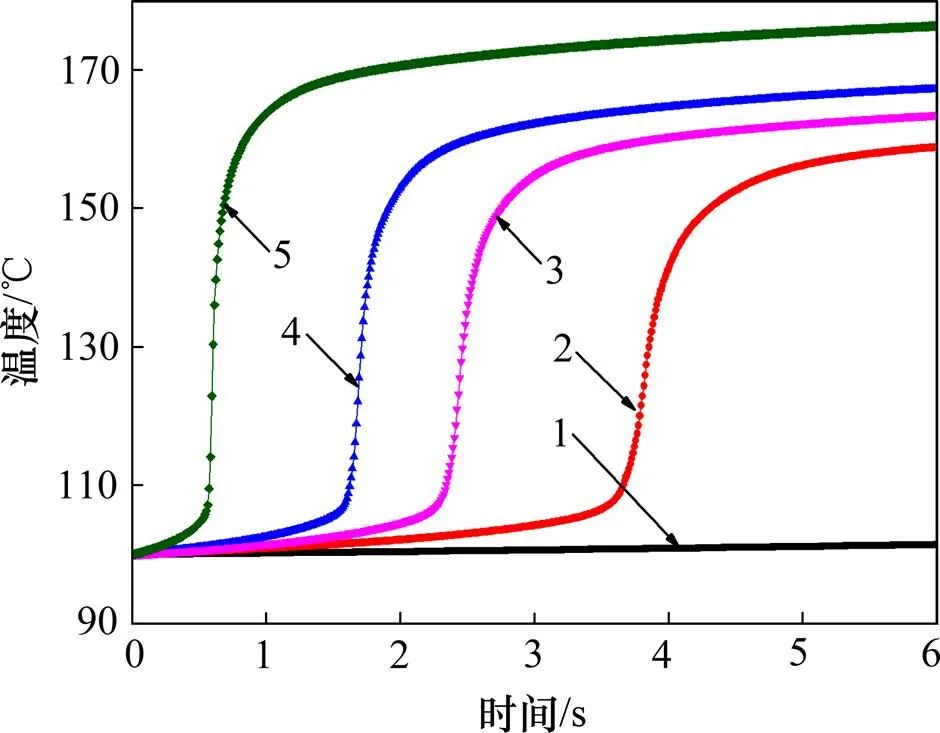
振幅/µm：1—10；2—20；3—30；4—40；5—50。

3.5 超声塑化过程中黏弹性生热的温度场

不考虑颗粒间摩擦生热，由于热传导作用塑化样品内部的黏弹性生热受塑化腔壁处摩擦生热的影响，因此有必要对黏弹性生热的温度场分布规律进行研究。塑化样品壁面处在工具头高频载荷下因剧烈摩擦，先于样品内部迅速达到并保持在黏流态。为简化计算，在不影响黏弹性生热温度场变化规律情况下，只考虑壁面处达到黏流态后对样品内部黏弹性生热温度场的影响，将模型壁面设置为170 ℃(略高于PMMA黏流温度)，模型初始温度设置为95 ℃，频率取20 kHz，施加随节点温度和位置变化的黏弹性热生成载荷(,)计算。

图8所示为1.2 s时工具头端面的黏弹性生热温度场分布情况。靠近壁面处聚合物因热传导最先达到玻璃化转换温度进入黏弹性生热快速升温阶段，径向温差明显，可见黏弹性生热在径向是由外之内的过程。图9所示为1.5 s时样品1/4纵向剖面温度场分布情况。样品在纵向亦存在较大温差，靠近工具头端面和腔壁处的温度最高，而芯部远离工具头端面部分的温度最低。这是因为工具头端面处黏弹性热生成率最高，能较快达到黏流温度，超声衰减对温度场影响作用明显。由此可见，壁面处的摩擦热和超声衰减会造成黏弹性生热过程温度场分布不均，塑化样品的黏弹性生热在纵向由工具头端面至样品底部，在径向是由外之内的过程。

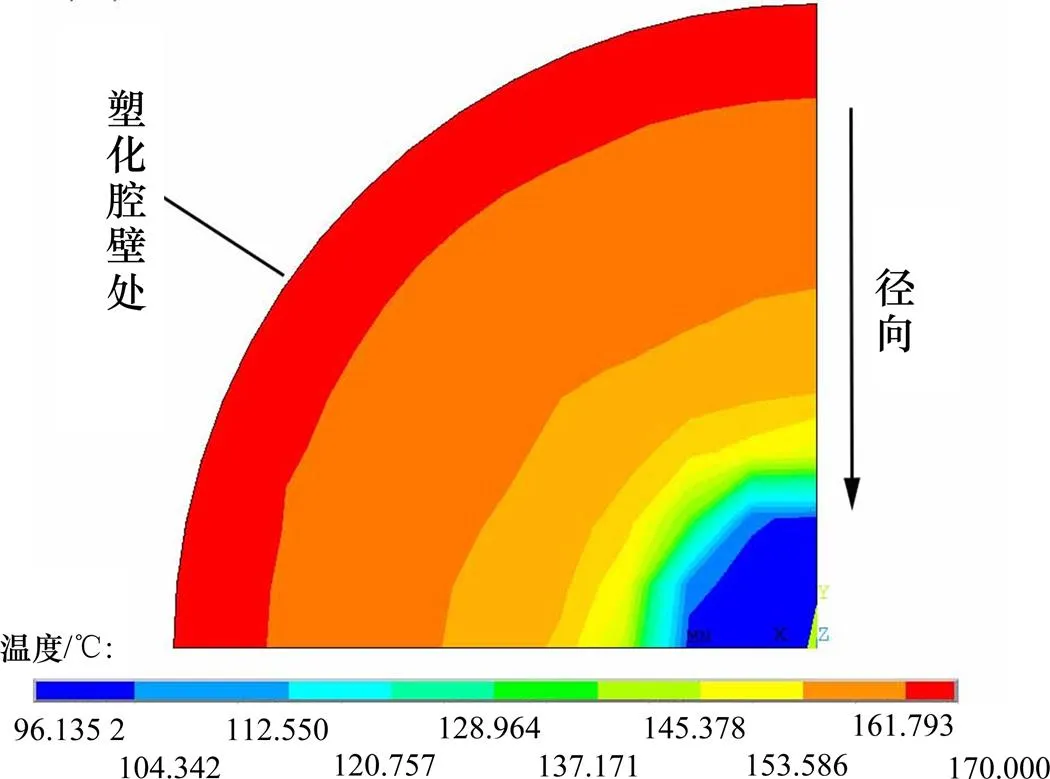
图8 工具头端面处温度场分布

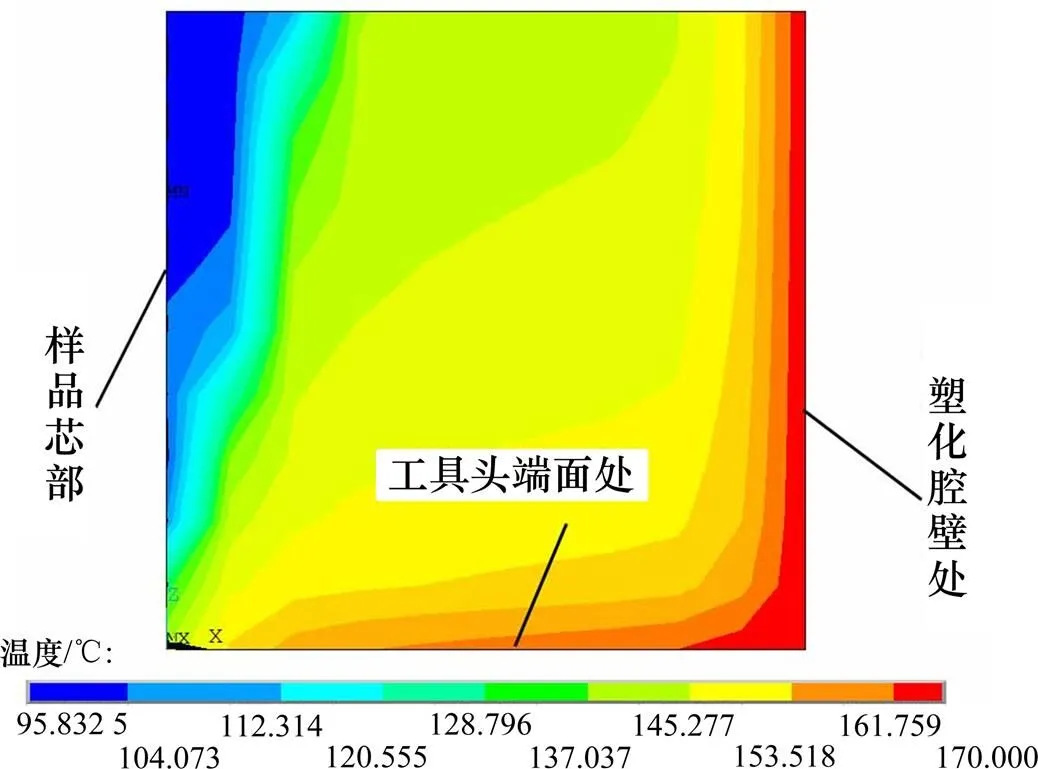
图9 塑化样品纵截面温度场分布

4 PMMA超声塑化形态演变实验

超声塑化过程颗粒形态变化时不同生热效应作用强度亦有变化，为分析黏弹性生热在聚合物从玻璃态到黏流态转变过程中的作用，采用自行设计的聚合物超声塑化实验装置完成塑化形态演变实验，如图10所示。塑化腔为圆柱形腔体；超声振动系统频率为20 kHz，超声发生器可调电压范围为0~300 V，最大功率为500 W；超声工具头与聚合物颗粒直接接触，材料为TC4钛合金；塑化对象为Mitsubishi Rayon公司生产的ACRYPET TF−9型PMMA；微塑件所需塑化量为毫克级，本文取400 mg。实验参数设置如表1所示，固定塑化压力和超声发生器电压，设置不同的超声作用时间，利用VMS−1510G影像仪观察对应塑化样品融化过程的形态演变，结合数值计算结果分析生热效应在塑化过程中的作用。

图10聚合物微注射成型超声塑化装置

表1 超声塑化形态演变实验参数设置

实验表明，PMMA颗粒形态在较短的时间内发生了很大变化。部分超声作用时间下的塑化样品工具头端面形貌图如图11所示(其中，图11(e)所示为塑化样品纵截面形貌)。从图11可见：超声作用后0.7 s内主要为PMMA颗粒界面的消融。初始阶段PMMA颗粒在高频载荷下剧烈摩擦，颗粒接触面处融化的聚合物并将颗粒黏结在一起。随超声持续作用，颗粒界面处融化量增加，在超声工具头压力下界面处空隙逐渐被填充。0.7 s时颗粒间界面间隙基本消失，塑化样品成为一个整体，但颗粒形态仍然可见(图11(b))，表明此时颗粒芯部并未达到黏流温度。

超声作用0.7 s以后塑化样品在径向呈现由外至内融化的现象。超声作用1.0 s后PMMA在径向融化效果差异明显，靠近塑化腔壁的PMMA达到均匀融化效果，而芯部位置未融化，部分颗粒形态依然可见。超声作用1.3 s后均匀融化的范围在径向有所扩大，芯部开始融化，颗粒形态基本消失(图11(d))。从图11(e)可以看出：距塑化腔壁和工具头端面越近，融化效果越好，芯部远离工具头处样品仍未完全融化，表明融化在纵向是自超声工具头向下的过程，这与前面黏弹性生热温度场分布的分析结果一致。

时间/s：(a) 0.2；(b) 0.7；(c) 1.0；(d) 1.2；(e) 1.5；(f) 2.0

颗粒界面消失后塑化样品作为一个整体在工具头作用下受迫振动，此时颗粒间摩擦生热作用消失，只有塑化腔壁处PMMA由于摩擦作用保持在黏流态之上。由于热传导作用壁面处摩擦热向芯部扩散，样品在径向先后达到玻璃化转变温度，进入黏弹性生热快速升温阶段。因此，在前期摩擦生热为黏弹性生热提供了激活热量，颗粒界面消失后样品内部的黏弹性生热是促使样品温度升高到黏流温度的主要生热效应。

5 结论

1) 超声塑化过程中不同阶段生热效应作用不同，超声作用初始阶段摩擦生热促使颗粒界面迅速融化消失并为黏弹性生热提供了激活热量；颗粒界面消失后黏弹性生热是促使样品温度升高到黏流温度的主要生热效应，因此选择合适粒径和形状的颗粒有助于聚合物在超声作用初期快速升高至玻璃化转换温度，提高塑化效率。

2) 黏弹性生热与聚合物力学性质密切相关，主要存在于聚合物玻璃化转换温度以上的一段温度范围。提高振幅会加快黏弹性升温速率，对应快速升温范围亦有所扩大；频率对黏弹性生热率最大值影响较大，但常见超声频率范围内提高频率对黏弹性升温历程影响较小。

3) 超声塑化过程样品从玻璃态到黏流态转变的融化是一个径向由外之内，纵向由超声工具头至下的过程，温度场分布不均，后续可考虑局部加热塑化腔改善。

[1] GIBOZ J, COPPONNEX T, MÉLÉ P. Microinjection molding of thermoplastic polymers: a review[J]. Journal of micromechanics and microengineering, 2007, 17(6): R96.

[2] MICHAELI W, OPFERMANN D. Ultrasonic plasticizing for micro injection moulding[C]//The Second International Conference on Multi-Material Micro Manufacture. Grenoble, France. 2006: 345−348.

[3] MICHAELI W, SPENNEMANN A, GÄRTNER R. New plastification concepts for micro injection moulding[J]. Microsystem Technologies, 2002, 8(1): 55−57.

[4] MICHAELI W, KAMPS T. Heating and plasticizing polymers with energetic ultrasound for micro injection molding[C]// Proceedings of the Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Orlando, FL, USA, 2010: 16−20.

[5] PLANELLAS M, SACRISTÁN M, REY L, et al. Micro-molding with ultrasonic vibration energy: New method to disperse nanoclays in polymer matrices[J]. Ultrasonics Sonochemistry, 2014, 21(4): 1557−1569.

[6] ZENG K, WU X, LIANG X, et al. Process and properties of micro-ultrasonic powder molding with polypropylene[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(1/2/3/4): 515−522.

[7] MICHAELI W, KAMPS T, HOPMANN C. Manufacturing of polymer micro parts by ultrasonic plasticization and direct injection[J]. Microsystem Technologies, 2011, 17(2): 243−249.

[8] JIANG Bingyan, HU Jianliang, LI Jun, et al. Ultrasonic plastification speed of polymer and its influencing factors[J]. Journal of Central South University of Technology, 2012, 19(2): 380−383.

[9] SACRISTAN M, PLANTA X, MORELL, et al. Effects of ultrasonic vibration on the micro-molding processing of polylactide[J]. Ultrasonics Sonochemistry, 2014, 21(1): 376−386.

[10] 刘小超. 聚合物超声塑化过程中声场及温度场分布研究[D]. 长沙: 中南大学机电工程学院, 2013: 12−20. LIU Xiaochao. Research on the acoustic and temperature field distribution of polymer ultrasonic plasticizing process[D]. Changsha: Central South University. College of Mechanical and Electrical Engineering, 2013: 12−20.

[11] NONHOF C J, LUITEN G A. Estimates for process conditions during the ultrasonic welding of thermoplastics[J]. Polymer Engineering & Science, 1996, 36(9): 1177−1183.

[12] BENATAR A, GUTOWSKI T G. Ultrasonic welding of PEEK graphite APC-2 composites[J]. Polymer Engineering & Science, 1989, 29(23): 1705−1721.

[13] MANO J F, VIANA J C. Stress–strain experiments as a mechanical spectroscopic technique to characterise the glass transition dynamics in poly (ethylene terephthalate)[J]. Polymer Testing, 2006, 25(7): 953−960.

[14] ZHANG Z, WANG X, LUO Y, et al. Study on heating process of ultrasonic welding for thermoplastics[J]. Journal of Thermoplastic Composite Materials, 2010, 23(5): 647−664.

[15] 何曼君, 陈维孝, 董西侠. 高分子物理[M]. 上海：复旦大学出版社, 2004: 358. HE Manjun, CHEN Weixiao, DONG Xixia. Polymer physics[M]. Shanghai: Fudan University Press, 2004: 358.

[16] TOLUNAY M N, DAWSON P R, WANG K K. Heating and bonding mechanisms in ultrasonic welding of thermoplastics[J]. Polymer Engineering & Science, 1983, 23(13): 726−733.

Viscoelastic heating effect in ultrasonic plasticization for micro injection molding

JIA Yunlong, JIANG Bingyan, PENG Huajian, ZHANG Sheng, LIU Xiaochao

(State Key Laboratory of High-Performance Complex Manufacturing, Central South University, Changsha 410083, China)

A mathematical model of viscoelastic heating in ultrasonic plasticization was built based on generalized Maxwell mechanical model with the consideration of ultrasonic damping. The viscoelastic heating rule of polymethyl methacrylate (PMMA) and temperature field distribution were studied through numerical calculation. The potency of viscoelastic heating was analyzed based on the results of both morphology evolution experiment and numerical calculation when the polymer transforms from glass state to viscous state. The results show that temperature of polymer has a significant effect on viscoelastic heating; the viscoelastic heating is especially noticeable when the temperature is between 105 ℃ and 150 ℃ for PMMA; the temperature field is uneven during the transformation process. Polymer close to the inner wall of plasticizing chamber and sonotrode are the first to reach the viscous flow temperature; friction heating is very noticeable in the initial phase, while the viscoelastic heating plays a major role when the interface of polymer particles disappears.

micro injection molding; ultrasonic plasticization; generalized Maxwell model; viscoelastic heating

10.11817/j.issn.1672-7207.2016.09.010

TQ320.66

A

1672−7207(2016)09−2976−08

2015−08−12；

2015−10−29

国家自然科学基金资助项目(91123012) (Project(91123012) supported by the National Natural Science and Technology of China)

蒋炳炎，博士，教授，从事高分子材料精密成型技术研究；E-mail: jby@csu.edu.cn

(编辑 赵俊)