Mathematica在矩阵初等变换中的应用

贾屹峰

（中国劳动关系学院数学与计算机教学部，北京100048）

Mathematica在矩阵初等变换中的应用

贾屹峰

（中国劳动关系学院数学与计算机教学部，北京100048）

在符号计算软件Mathematica平台上，实现矩阵的初等变换，并被引入到课堂教学中，在提高教学效率的同时，激发学生的兴趣，提高学习成绩。

Mathematica；线性代数；矩阵；初等变换

0　引言

在《线性代数》的教学中，利用矩阵的初等变换，特别是初等行变换，可以计算行列式的值，求矩阵的秩、方阵的逆、向量组的向量极大无关组和向量的线性表示，以及解线性方程组。《线性代数》是一门重要的基础课，是后续一些知识学校的基础。因此，矩阵的初等变换线性代数非常重要的内容。

在矩阵初等变换的教学过程中，为学生演示初等变换的过程是必要的，传统的板书教学，每进行一次变换，必须写一个矩阵，算法虽然不是很复杂，但是计算比较繁琐，而且整个过程需要耗费大量宝贵的课堂时间。即使是具有多年教学经验的教师，对于任意给出的一个矩阵，也不能保证每一步计算都完全正确。如果利用PowerPoint、Flash等多媒体教学手段，目标矩阵和每一步的过程都必须在课前完成，教学过程是将预先计算好的过程逐步显示出来，而且不能随意更改，虽然出错的可能性很小，节省了时间，但是缺少了灵活性，不能对任意矩阵施以任意的初等变换。

为了进一步提高教学质量，让学生更好地理解矩阵初等变换的重要性，熟练掌握计算过程及其应用，我们将符号计算软件引入到教学过程中，在减少了课堂教学中的复杂计算，节省了时间的同时，又增加了互动，激发了学生的学习兴趣，从而丰富了教学手段，提高了学习成绩。

Mathematica是一种集成化的符号计算软件系统，具有多种数据结构和丰富的数学函数，主要功能包括三个方面：符号演算、数值计算和绘制图形。而且在这该件平台上，还可以进行二次开发，根据需要编写相应的程序。在本文中，我们利用自己所编写程序，完成了矩阵的初等变换功能，而且根据需要，不但可以显示每一步的计算过程，而且还可以具体对矩阵的某一行或某一列单独进行变换。所编写的程序可以对任意的矩阵都可以完成，可以进行交互式的操作，使用灵活方便。

1　交互式矩阵初等变换的Mathematica实现

1.1矩阵的输入输出和操作

Mathematica软件本身有一些直接对矩阵进行基本计算和操作的函数，例如Det用以计算方阵的行列式；MatrixRank直接给出矩阵的秩；RowReduce将矩阵化为行最简形式，矩阵的乘法可以用Dot或者“.”给出；对于一个非奇异方阵，Inverse直接给出其逆矩阵，但是如果是奇异矩阵，则会说明该矩阵式奇异的。Mathematica还有其他一些有关矩阵计算的函数，上述函数只是矩阵最基本的一些计算，这些函数被引入到线性代数课堂教学中，用以验证手工计算的正确性。

矩阵的初等变换是对矩阵的行或列施以的运算，而在Mathematica中，矩阵是以二维表的形式存在，因此，用Mathematica完成矩阵的初等变换实际是对表的元素进行运算。对于矩阵A=｛0，1，-1｝，｛-6，2，-2｝，｛1，-2，1｝｝，A［i］表示取出A的第i行，A［i，j］表示取出第第i行，第j列的元素。例如A［2］输出｛-6，2，-2｝，A［2，3］输出-2。Take从表中取出元素，Delete是从表中删除元素，Append和Insert是向表中添加元素，这些函数的参数是对表中某一个或几个元素、一个位置或几个位置进行添加或者删除，具体的例子可以参考帮助文件。用Mathematica完成矩阵的初等变换主要就是利用这几个函数完成。

1.2交互式矩阵初等变换

我们把矩阵A的第i行（或列）乘以k，称为第一种初等变换，记为ri→krj（或ci→kcj）；交换矩阵A第i行（或列）和第j行（或列），称为第二种初等变换，记为ri↔rj（或ci↔kcj）；矩阵A的第i行（或列）乘以k，加到第j行（或列），称为第三种初等变换，记为rj→kri+rj（或cj→kci+cj）。

下面的函数给出了在Mathematica上实现矩阵第一种初等变换的源代码：

其中参数M1表示所要变换的矩阵；ith是被乘的行（或列）；当参数r输入为row时是行变换，输入col时是列变换；k是乘数。

第二种初等变换的函数的源代码为：

其中参数M2表示所要变换的矩阵；第ith行（或列）与第jth行（或列）交换；当参数r输入为row时是行变换，输入col时是列变换。

第三种初等变换的函数的源代码为：

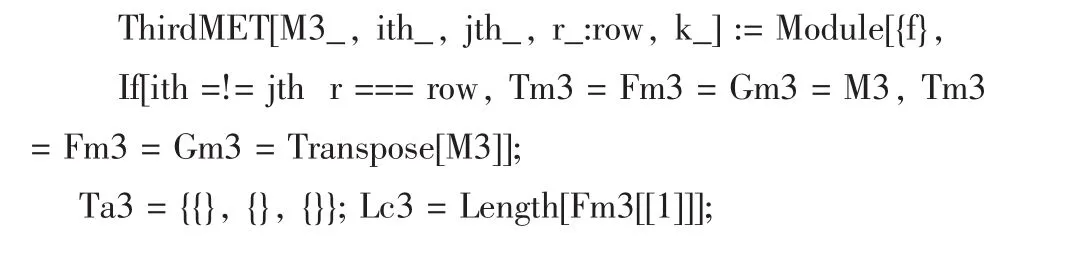
其中参数M3表示所要变换的矩阵；第ith行（或列）乘以k加到第jth行（或列）交换；当参数r输入为row时是行变换，输入col时是列变换，k为乘数。

为了更好地显示计算过程，对相应的行（或列）的字体进行了加粗，字体的颜色分别用蓝色、绿色和红色显示，显得更为醒目。

下面利用上面的函数对上一目的矩阵A进行初等变换。

上述过程可以继续，直到得到想要的矩阵形式，而且这些函数还可以嵌套使用。这两个函数是对矩阵进行初等行变换，对初等列变换，可以利用转置矩阵完成。

2　矩阵三角化的Mathematica实现

2.1矩阵的三角化

矩阵的初等变换在计算行列式、求矩阵逆和秩、解线性方程组、向量的极大无关组以及向量的线性表示等方面有着重要的应用。在这些计算中，通过矩阵的初等变换，将矩阵化为上三角形式或下三角形式，直接得到矩阵的秩、行列式的值等，或者在此基础上再进一步利用初等变换，将矩阵化为对角形式或行最简形式。Mathematica内置函数可以直接得到结果，例如RowReduce可以将矩阵约化为行最简形式，MatrixRank可以直接求出矩阵的秩等，但是这些函数都是直接给出结果，而没有计算过程。

下面首先给出的函数，可以将矩阵化为上三角形式，

其中参数M0为一只矩阵，cn根据需要输入参数，当cn=-1时，用于计算矩阵的逆，计算过程会自动添加相应的单位矩阵，输出的结果是一个三角化的矩阵，矩阵的逆需调用后面的回代函数进一步计算；当cn=0时，用于计算行列式的值，或者矩阵的秩，返回值是1，或者？1，表示在计算过程中交换行，行列式需要变号，行列式的值为计算过程的最后结果矩阵对角线元素与输出结果的乘积；当cn为其他值时，可以用于计算向量组的极大无关组、求解线性方程组（需要调用回代函数）、矩阵的秩等，这些直接从计算过程的最后结果可以看出，返回值是一个上三角形式的矩阵。

通过上面的MatrixTriReduce函数，可以将矩阵化为上三角形式，但是如果要计算矩阵的逆、求解线性方程组、矩阵方程，或者向量的线性表示，还需用下面的回代函数，输入的参数M2是MatrixTriReduce的返回值。

当输入的参数跑p=-1时，函数的返回值是矩阵的逆，其他值时，是矩阵M2的行最简形式，从最简形式可以直接看出线性方程组的解，或者向量组的极大无关组。

2.2计算实例

下面给出上面两个函数的计算实例。

例1计算上一节矩阵A的行列式。

上述过程的最后结果是一个上三角行列式，矩阵A的行列式的值为矩阵对角线元素的乘积，再乘以返回值-1。即|A|=-6。

例2求向量组

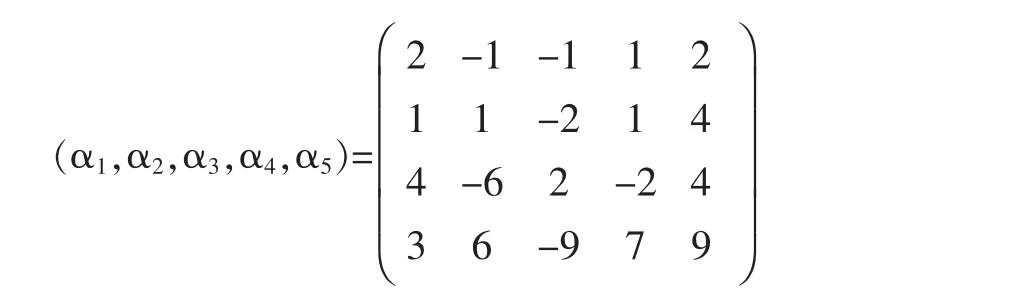
的极大无关组，并将其余向量用极大无关组线性表示。

首先用MatrixTriReduce［A，0］函数将矩阵化为上三角形式，返回值为B=｛｛2，-1，-1，1，2｝，｛0，3/2，-3/2，1/ 2，3｝，｛0，0，0，-8/3，8｝，｛0，0，0，3，9｝｝，再调用函数Matrix-Substituion［B，1］化为最简形式

有计算过程的最后一个矩阵，或者返回值很容易得到α1，α2，α4，是极大无关组，且α3=-α1-α2，α5=4α1+ 3α1。两个函数还可以嵌套使用。

类似，用这两个函数还可以求解矩阵的逆、线性方程组、矩阵方程等。

3　结语

上述程序的使用面比较广泛的，不限于矩阵元素是数字，矩阵元素是符号也依然可以使用。另外可以在教学中使用，在科研中也可以。

上述程序已在教学中得到了实际应用。Mathematica在线性代数教学中的应用不仅仅限于矩阵的初等变换，在线性代数的教学中，行列式、线性方程组、矩阵、向量的线性相关性，以及计算矩阵的特征值、矩阵对角化都得到了应用，均收到了很好的效果。

本文中的程序实在Mathematica5.1版本上编写的，如果利用更高的版本，源代码可能更简洁。

［1］赵树嫄.经济应用数学基础（二）.线性代数.中国人民大学出版社.第二版，2008.5.

［2］张韵华，王新茂.Mathematica 7实用教程.中国科学技术大学出版社，2011，1.

Application of Mathematica in Elementary Transformation of Matrices

JIA Yi-feng

（Department of Mathematics&Computer Teaching，China Institute of Industrial Relations，Beijing 100048）

Realizes the elementary transformation of Matrices in symbolic compute platform Mathematica，and it's introduced to the classroom teaching，increases the efficiency of teaching，excites the interest of students，and improves the performance.

Mathematica；Linear Algebra；Matrix；Elementary Transformation

2011年中央高校基本科研业务费专项基金项目（No.11zy063）

1007-1423（2016）25-0017-05DOI：10.3969/j.issn.1007-1423.2016.25.004

贾屹峰（1972-），男，陕西西安人，博士，研究方向为符号计算