深度理解面积关系逐步提升解决问题水平

陈晶

【摘 要】学生解決某一问题时，能够呈现出多样的答案，并非一日之功，需要教师整体把握某个单元、某一领域知识之间的前后关联，在前面学习的过程中，不断积累思考问题的经验，学生在后续解决问题的过程中才会呈现多样的答案。

【关键词】初步判断；深度理解；灵活运用

中图分类号：G623.5 文献标识码：A 文章编号：1671-0568（2016）25-0095-03

一位教师在执教“苏教版”小学数学五年级（上册）第26页第3题（如图1）的过程中，直接出示题目让学生解答。从最后解答的情况来看，学生在画平行四边形的时候，全班50位同学，有48位同学画出了底与长方形的长相等，高与长方形的宽相等的图形，仅有2位同学找到了其他的画法；画三角形的过程中，能够一次就画对的只有22人，有20人经过反复调整才画对，还有8人画出了错误的图形；画梯形的过程中，能够一次就画对的只有12人，有24人经过了多次调整才画出了正确的图形，还有14人没有能够找到正确的答案。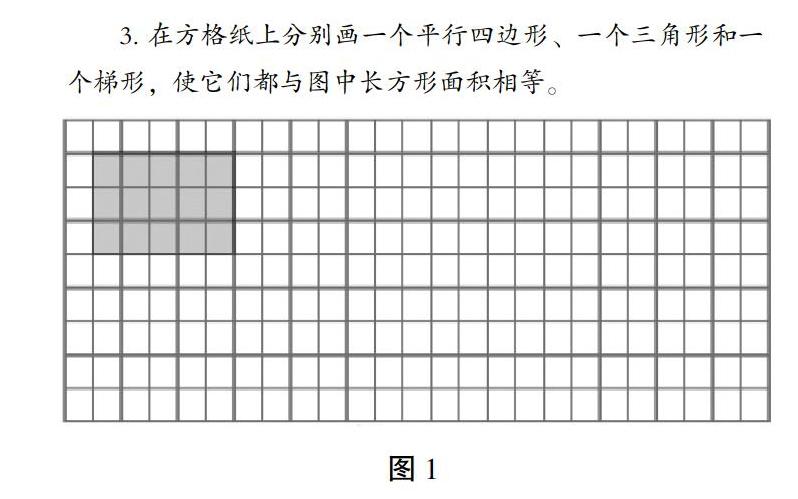

从解决问题的过程可以看出，学生在学习三角形、平行四边形和梯形的面积时，仅仅能够运用公式进行计算，但是没能深度理解三种图形面积之间的关系，在遇到类似问题的时候，解决问题的方式单一，过程冗长，不容易找到正确的答案。如何让学生深度理解图形面积之间的关系，提升学生解决实际问题的能力呢？在教学的过程中，笔者从这样几个方面进行了尝试：

一、初步运用公式过程中，理解同一类图形面积之间的关系

在平行四边形、三角形和梯形面积公式推导的过程中，学生初步理解了转化前后图形面积之间的关系。在初步运用公式解决问题的过程中，还需要把关系进一步向前推进，深度理解同一类图形面积之间的关系。可以通过以下三个层次进行：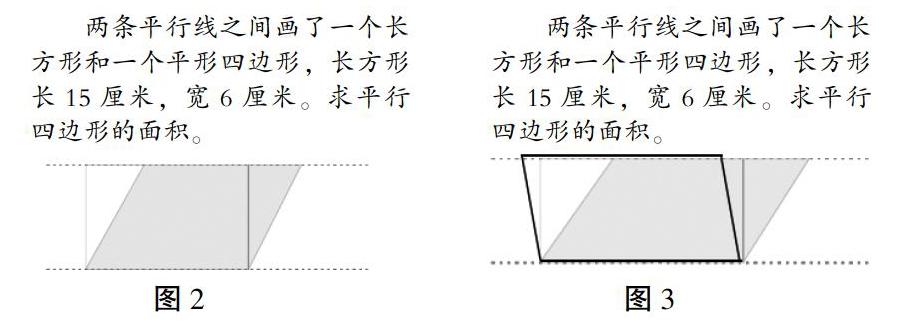

1. 根据图形形状直观把握关系

在学生会利用公式计算图形面积后，可以先通过变式练习，让学生感受到同一类图形面积相等之间的关系。例如，在学生知道了平行四边形的面积计算公式后，在学习教材第8页的“练一练”（如图2）的过程中，可以这样进行：先出示图2中的题目，让学生初步体会长方形和平行四边形的面积相等；然后在两条平行线之间再画出一个平行四边形（如图3），说一说这两个平行四边形相等的理由；最后再尝试着找一找与这个平行四边形面积相等的其他平行四边形。最终体会到等底等高的平行四边形面积都相等。

在学习了三角形的面积公式之后，通过类似的方式让学生体会到等底等高的三角形面积相等；在学习了梯形的面积公式之后，也让学生体会到两个梯形上底和下底分别相等，高也相等，那么这两个梯形的面积相等。通过这样的练习，让学生能够根据图形形状，直观把握同一类图形面积相等的关系。

2. 根据计算过程分析关系

在学生初步理解了面积相等的同一类图形之间的关系后，还需要进一步丰富学生的认识，让学生能够根据计算面积的过程判断图形之间的相等关系。对平行四边形的面积关系，可以这样来教学：首先出示图4，让学生想一想：这两幅图的面积相等吗？为什么？利用前面的经验，有些学生判断相等，有些学生判断不相等，然后出示图5，让学生联系公式计算面积的过程分析这两幅图的面积是相等的。

通过这样的练习让学生理解：面积相等的平行四边形不仅仅有等底等高这样的情况，如果另一个平行四边形的底与这个平行四边形的高相等，另一个平行四边形的高与它的底相等，那么这两个平行四边形面积相等。让学生从面积计算的过程去体会面积相等的现象，利用乘法的交换律去解释相等的原因。同样可以分析其余两类图形面积相等的关系：如果两个三角形的底和高数据交换，那么这两个三角形的面积相等；如果两个梯形的高与上底与下底的和数据交换，那么这两个梯形的面积也相等。通过这样的练习，借助于乘法交换律，从计算面积的过程去分析面积之间的关系，丰富对同类图形面积之间关系的认识。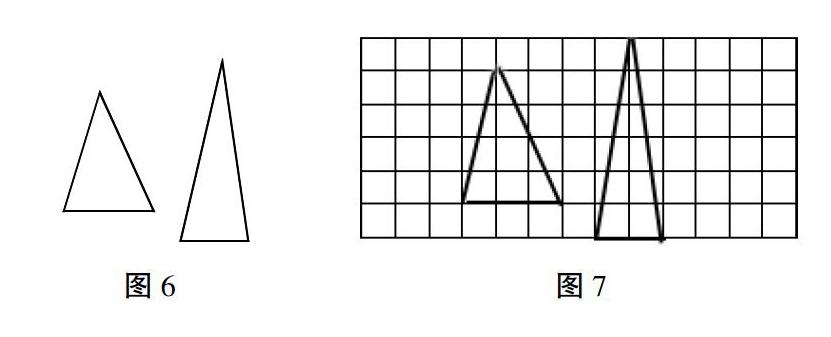

3. 根据计算结果理解关系

在学生借助前面两层经验理解同一类图形面积之间的关系后，还需要进一步提升学生的分析水平，让学生从计算的结果去理解图形面积相等的关系。对三角形的面积相等之间的关系，可以这样来体会：首先出示图6，让学生判断下面这些图形的面积相等吗？学生联系前面的经验，想到既不是等底等高，也不是把底和高交换数据，大部分学生会判断不相等。然后出示图7，通过计算可以知道，如果发现底和高的乘积相等，那么这两个三角形的面积相等。

在梯形的面积学习结束后，让学生体会到，只要两个梯形上底与下底的和与高的积相等，那么这两个梯形的面积相等。通过上述过程，进一步提升学生对面积相等的认识，从计算的结果理解同一类图形面积之间的关系。

二、在灵活运用公式过程中，理解不同类图形面积之间的关系

在学生理解了同类图形面积相等之间的关系后，还需要让学生理解不同类图形面积相等之间的关系，丰富学生对面积相等之间关系的认识。可以从这样三个方面进行：

1. 理解平行四邊形与长方形之间的关系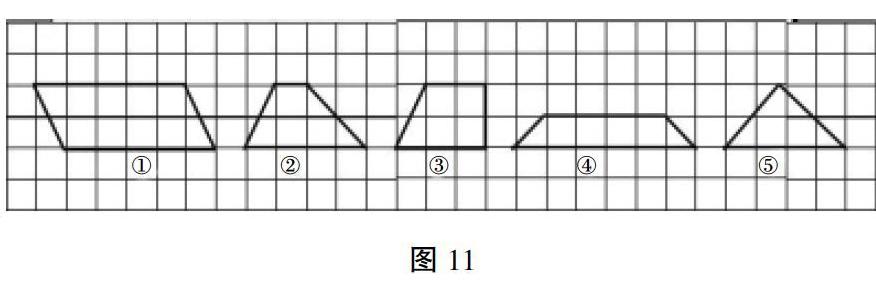

在学习推导公式的过程中理解了转化前后长方形和平行四边形面积之间的关系，在后续学习过程中，还需要进一步提升学生的认识，发现两者面积相等的其他因素。在教学教材第11页第1题（如图8）教学过程中，可以通过这样几个层次的学习让学生体会到两者面积之间的关系：

首先，让学生不计算长方形的面积，直接画出与长方形面积相等的平行四边形，学生根据前面的经验想到：可以画一个底与长方形的宽（或长）相等，高与长方形的长（或宽）相等的平行四边形；然后，引导学生向深度思考，如果可以算出长方形的面积，你能够找到哪些与长方形面积相等的平行四边形？在学生算出长方形的面积是12格，联系平行四边形的面积计算公式思考，找到（ ）×（ ）=12，这里的两个数分别做平行四边形的底和高，画出的平行四边形就符合要求了。通过这样的练习，让学生从凭借直观分析去解决问题走向运用推理去解决问题，提升对两者之间关系的认识。

2. 理解三角形与平行四边形之间的关系

在面积推导的过程中，学生理解了转化前后三角形与平行四边形面积之间的关系。在练习的过程中，还需要进一步丰富学生对三角形的面积与平行四边形面积之间关系的认识。在教学教材第12页第7题的过程中（如图9），可以安排这样三个教学过程：

首先只出示（图10），让学生想一想：有一个三角形的面积是平行四边形面积的一半，这样的三角形可能是什么样子？学生根据前面的经验想到一定是等底等高。接着出示图9，通过判断的过程，让学生知道三角形的面积是平行四边形面积的一半，三角形不一定与平行四边形等底等高。然后联系面积公式想到，只要三角形底与高的积是平行四边形底与高积的一半，那么三角形的面积就是平行四边形面积的一半。最后再想一想：如果一个三角形与这个平行四边形面积相等，会是什么样的图形？学生想到如果三角形的底与平行四边形的底相等，高是它的两倍，两个图形的面积相等。也可能想到三角形的高与平行四边形的高相等，但是底是它的两倍，这两个图形的面积相等。进一步推广，如果三角形的底与高的积是平行四边形底与高的积的两倍，那么三角形和平行四边形的面积相等。通过上述过程，让学生从三角形是平行四边形一半的关系走向两者相等的关系，逐步加深了对两者面积之间关系的理解。

3. 理解梯形与平行四边形、三角形之间的关系

学生在面积公式推导的过程中，理解了转化前后梯形与平行四边形的关系后，还需要进一步深入理解平行四边形与梯形面积之间的关系，并且建立梯形的面积与三角形面积之间的关系。可以通过这样三个层次的练习：

第一层次：首先只出示图11中的平行四边形（1号图），让学生想一想：一个梯形的面积是它的一半，这个梯形可能是什么样子？然后出示2号图与3号图，学生首先想到如果梯形的上下底的和与平行四边形的底相等，高与平行四边形的高相等，那么梯形的面积是平行四边形面积的一半。出示4号图形，让学生进一步推广，如果梯形上下底的和与高的积与平行四边形的底与高的积相等，那么梯形的面积是平行四边形面积的一半。第二层次：让学生想一想，如果一个梯形的面积和这个平行四边形的面积相等，这个梯形可能是什么样子？让学生联系面积推导的过程进一步体会到，如果梯形上下底的和与高的积是平行四边形底与高的积的2倍，那么梯形的面积与平行四边形面积相等。第三层次：让学生思考，一个三角形与3号图的面积相等，这个三角形可能是什么样子？在学生思考后，出示5号图，并且得出结论：只要三角形的底与梯形上下底的和相等，三角形的高与梯形的高相等，梯形的面积就与三角形的面积相等。进一步推广，只要三角形的底与高的积与梯形上下底的和与高的积相等，这两种图形的面积就相等。通过这样三个层次的研究，进一步丰富平行四边形与梯形面积之间关系的认识，并且建立三角形与梯形面积之间的关系。

三、在综合运用过程中，逐步提升解决问题的水平

在学生理解了图形面积之间的关系后，在设计与长方形面积相等的三角形、平行四边形和梯形的过程中（如图1），也需要分层安排学生解决问题的过程，逐步提升学生解决问题的水平。在教学过程中，可以这样处理：

第一层次，不计算长方形的面积，你能够直接画出与长方形面积相等的平行四边形、三角形和梯形吗？

第二层次，算出长方形的面积，你还能想到画出哪些与长方形面积相等的平行四边形、三角形和梯形？

上述第一个层次，让学生不计算，依据直觉去画图，再找与长方形面积相等的平行四边形，直觉就是底与长方形的一条边相等，高与长方形的另一条边相等。如果三角形的底与长方形的一条边相等（或2倍），高是另一条边的2倍（或相等），那么三角形的面积与长方形相等。如果梯形上下底的和与长方形的一条边相等（或2倍），高是长方形另一条边的2倍（或相等），那么梯形的面积与长方形的面积相等。第二个层次，如果可以计算长方形的面积，则可进一步丰富思考问题的过程，如果平行四边形的底与高的积与长方形长与宽的积相等，那么平行四边形的面积与长方形的面积相等；如果三角形的底与高的积是长方形长和宽积的2倍，那么三角形的面积与长方形的面积相等；如果梯形上下底的和与高的积是长方形长和宽积的2倍，那么梯形和长方形的面积相等。通过上述两个层次的要求，丰富了学生解决问题的思路，逐步提升了学生解决问题的能力。

学生在解决一个问题背后能否有多样的答案，并非一日之功，需要教师整体把握某个单元或者某一知识的前后联系。在前面学习的过程中，不断积累学生思考问题的经验，打通知识之间的关联，在后续的解决问题的过程中才会呈现出丰富的答案。

（编辑：张 婕）