把脉学习细节，共振数学思维

单广红

【摘 要】数学课堂是由师生双边互动的许多细节构成的，教师要对生成的新信息把脉准确到位，灵活调控，使师生思、情、志达到高度统一，产生“思维共振”效应，在追问、交流、留白与辨析中，不断催生新观点，使课堂学习精彩纷呈。

【关键词】学习细节；思维共振；追问；耐心；留白；辨析

中图分类号：G623.5 文献标识码：A 文章编号：1671-0568（2016）25-0026-03

所谓 “思维共振”，是指课堂交流中师生的思、情、志得到了高度统一 ， 完全进入一种高度亢奋、 心理相融的精神状态。这种在交流中产生的思维碰撞和协同效应，从而各自围绕共同的问题进行创造性思维，使“不同而和”的新观念脱颖而出，这种效应在教学中叫“思维共振”。在指导学生学习的过程中，教师如果能把握好可能产生不同观点和思想的学习细节，引导学生在交流中产生思维共振，课堂上将会精彩纷呈，惊喜不断。那么小学数学课堂应关注哪些细节？如何让学生产生思维差异？笔者想在此谈一谈调研及教学中的一些想法。

一、拐点处多些追问，调整共振频率

数学课堂是由学生产生的许许多多问题构成的。有的是不懂，有的是不会，有的是质疑，有的是反问，还有的是追问。如果教师能够捕捉时机，恰到好处地进行拐弯，调整共振频率，不懂的重新学习，不会的再次思考，质疑的改变角度，反问的变换方向，追问的继续向前，会使学生的思维状态更活跃，学习气氛会一个高潮接着一个高潮。如下述案例：

案例一：苏教版三上“分数的初步认识（一）”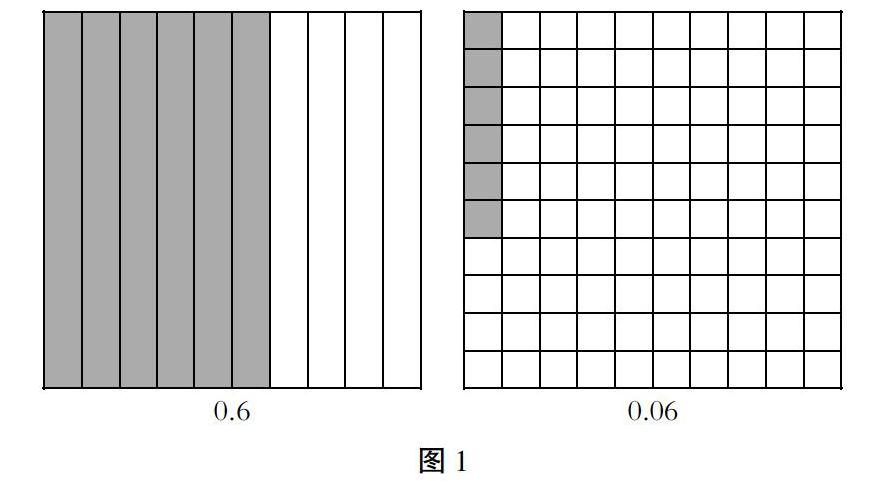

课件呈现对话场景。喜洋洋：分给你月饼的。 懒洋洋：不行不行，我要！

师：看到这个对话，你想到什么？

生1：懒洋洋贪心！

生2：我觉得比少。

师：为什么呢？

生2：因为一条线，要2条线，4个小块，不到一半。

师：大家拿出月饼的纸片，分给懒洋洋看看。

课件：村长、灰太狼……大伙儿都来了，这下懒洋洋开心吗？

生：不开心，人多分得更少了。

师：这时他吃到多少？

很符合小学生的认知特点。教师并没有急着下结论，而是把球“踢”给学生，要求他们动手操作：拿出月饼的纸片，分给懒洋洋看看。学生在亲历实践中验证猜想，感受到“同样大的月饼，分的份数越多，其中的一份就越小，所以”。但教师仍未就此罢休，而是相继来了8个小动物分蛋糕，追问“这下懒洋洋开心吗？”及时让学生积累的学习经验加以运用。此教学片断中，教师在拐点处持续的几个追问，把学生只可意会不可言传的第一“直觉”转化成“感知”，通过“猜想—操作—验证—归纳”上升成“认知”，逐步发现数学本质。这些追问，有“峰回路转”之感，有“拨云见日”之效。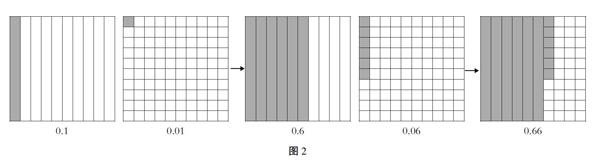

二、交流时多些耐心，保持共振和谐

在日常课堂或公开课上，“替代思维”现象较为普遍。所谓“替代思维”，就是甲的思维方法取代了乙的思维。一般存在两种情况：1.教师的思维替代了学生的思维；2.优生的思维替代了后进生的思维。在教学中，倾听学生的回答再多些耐心，不要轻易地打断学生回答，不要剥夺学生发言表达的权力，而是站在学生的角度去审视一些问题，会发现他们的视角更独特，表达更简洁。只有读懂学生思维，才能保持共振和谐。

案例二：苏教版五上“小数的计数单位和数位顺序表”

课件呈现图1：下面图形都表示整数“1”，分别涂色表示“0.6”和“0.06”。

师：1里面有几个0.1？

生：1里面有10个0.1。因为正方形被平均分成10分，其中1份是0.1，一共有10份。

师：0.1里面有几个0.01呢？为什么？对照图说说你是怎么想的？

生：0.1里有10个0.01。因为把1条平均分成10格……

师：（打断学生回答）我知道你的意思了，把整数“1”平均分成10分，1个竖条就是0.1，0.1又分成10份，整数“1”一共分成100份，一份就是0.01，一条又是10份，所以0.1里有10个0.1。是不是？

生：（似懂非懂地点点头）是……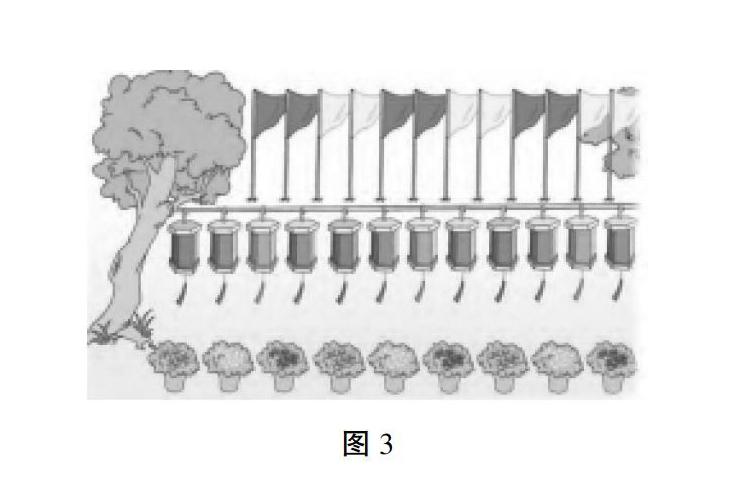

學生真的和教师想的一样吗？细细分析会发现，教师并没有听懂学生的意思，而是“硬拉”到成人的思考视角：“1”里面有10个“竖条”，即10个0.1，“1”里面又有100个“小方块”，即100个0.01，100里面有10个10，所以得到结论“0.1里有10个0.01”。其实学生是用自己看到的直观模型来解释的。在学生的眼中“0.1”是1个“直条”，“0.01”是1个“小方块”，1个“直条”正好平均分成了10个“小方块”，所以“0.1里有10个0.01”。因为这样的回答偏离了教师的预设答案，这位教师用“替代思维”硬拉回到预设流程上去，把简明精彩的思考“拉偏”。教学中这样的现象很多，教师不能静等学生把话说完，常“接过话茬”而失去宝贵的生成资源。如果教学时创造性地使用教材，把教材的呈现顺序稍作调整：先引导学生通过图来认识“0.1”和“0.01”以及两个小数单位间的关系，这是关于小数知识的上位学习；再让学生在两幅图中涂出“0.6”和“0.06”；最后把这两幅图动态融合成一幅图，变出“0.66”（如图2所示），学生会深刻理解这两个“6”的位置不同，表示的意义是不一样的，用他们的经验来解释：十分位上的“6”是6个“直条”，百分位上的“6”是6个“小方块”。这样可以用学生的语言，表达出长期困扰教师无法“言传”的“位值”问题，后续学习的多位小数采用“类结构”进行推理，则迎刃而解了。

三、探索时多些留白，拓展共振幅度

教学艺术在于“点石成金”，把“讲堂”变成“学堂”。目前有不少教师在课堂上怀疑学生的学习能力，一节课一直喋喋不休，学生失去了独立思考和反刍的时间，学习效果与预设相差甚远。长此以往，学生习惯当“听众”，新知探索缺少积极性和主动性。所以课堂上应适时给学生留白，培养学生举一反三，触类旁通，拓展共振幅度。

案例三：苏教版四上“简单的周期”

课件呈现图3。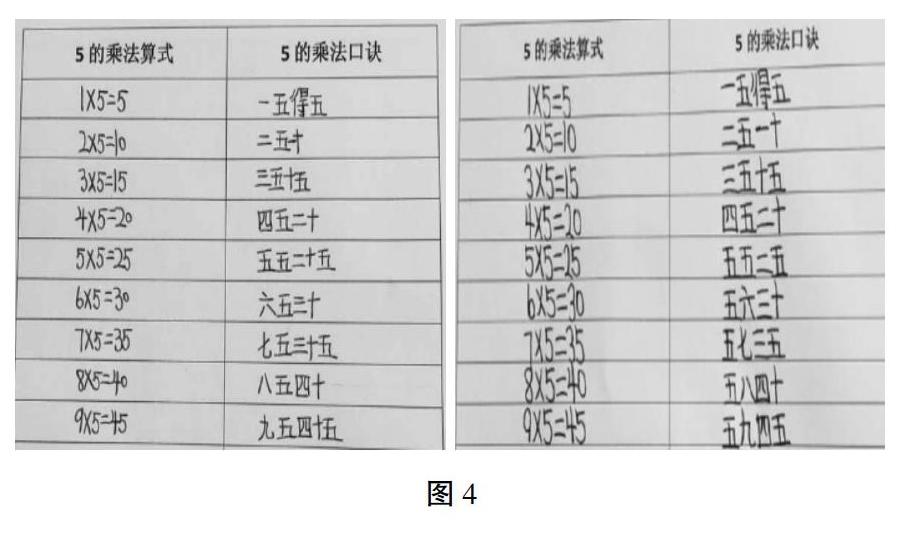

师：你看到了什么？

生：彩灯、鲜花、和彩旗。

师：它们排列有什么特点？

生：都是循环的。

师：盆花是几个一组？第10盆是什么颜色？

生：盆花每3盆一组，分别是按红、黄、蓝的顺序排列的。第10盆是蓝色。

师：第19盆呢？把自己的方法画在纸上。

生1：△□〇 △□〇 △□〇 △□〇

△□〇 △□〇 △

生2：ABC ABC ABC ABC ABC ABC A

生3：藍黄红 蓝黄红 蓝黄红 蓝黄红 蓝黄红 蓝黄红 蓝

生4：19÷3=6（组）……1（盆）

师：19里面有6个3还是3个6？余下的1盆在第几组？

……

执教教师有意识地把盆花、彩灯、彩旗分成三个层次进行教学。但在教学过程中，三个板块平均用力，都是从头问起，“一扶到底”。如果教师在盆花问题上引导学生观察多种想法与算式之间的联系，让学生发现余数是几，就看这一组的第几盆，而每一组排列的顺序是一样的，所以也可以看第一组的第几盆。学生发现并理解这一规律后，彩灯图和彩旗图大胆留白，让学生在刚积累的学习经验基础上，用“类结构”进行推理。建议作如下设计：1.彩灯图放手让学生自主解决如果算式正好整除没有余数，怎样判断“第x盏是什么颜色”；2.彩旗图可以在彩灯图的基础上再次拓展，“第x面是什么颜色，其中红色有几面？黄色有几面？”通过这样的调整，设计有层次，探索有坡度，学生在学结构用结构过程中，充分利用“留白”时间，在内省思考中将数学学习引向纵深。

四、反馈时多些辨析，明晰共振波长

畅通良好的反馈机制是一节好课最基本的保障。教师要多走近学生，了解他们遇到什么困惑，容易犯哪些错误，多听听他们是怎样想的。所以，反馈不是简单的比对答案正确与否，而是从差异思考中收集学习素材引导辨析，或方法优化，或辨错纠错，或完善规则等。在作业反馈时，教师要用宽容之心，呵护学生初始萌芽的创新思考，然后委婉地提出科学与规范的要求，明了共振波长，使数学思考更精准。

例如，有位教师在执教苏教版二上“5的乘法口诀”时，采用了“大九九”教学策略。在让学生自主列算式编口诀环节，她同时呈现了这两份作业，让学生观察后提提建议（如图4）：

通过观察发现，两名学生思考都很有序，第一位学生从上到下都是按“几五”的格式编的口诀；第二位学生根据前一课时的学习经验，发现口诀一般先说小数再说大数更顺口，所以把“六五三十”这一类口诀改成“五六三十”，全班统一了认识，并和我国传统的文化习惯相对接。但是“五五二五”“五七三五”和“五九四五”应写成“五五十十五”“五七三十五”和“五九四十五”。在这样并联呈现的练习反馈中，把学生最容易出现的典型问题暴露出来，进行辨析思考，扬长避短，完善认知结构。

再如，有一位教师执教苏教版三上“两位数除以一位数”时，让学生用自己的方式表示怎样算“46÷2”，学生有很多不同的表达方法，教师收集并呈现如下：

如果用成人的眼光看，前两种做法看上去很不靠谱，会直接评价学生算法错误。但结合学生的学习经验看，在学习“两位数除以一位数”的前一节课，他们刚学过“整十数除以一位数的口算”，二年级又学习过“商是一位数”的表内除法，这两次学习都是一次完成写商。所以，在竖式上只会表达除一次的结果。从他们的书写中发现已有两步计算的初步意识：把46分两次去除。先把“40”平均分成两份，再把“6”平均分成2份。限于现实经验，他们把第一次除得的结果在竖式中表示出来，第二次除得的结果不会在竖式中表示，其实已在脑中完成了。第三种算法已基本接近课本中的要求，机智地用“一次写商”解决了“两次写商”的困难。第四种算法通过分小棒图得出计算结果。最后两种算法看上去不一样，其实表达的是一个意思，前一种表达的是“6个一除以2得3个一，4个十除以2得2个十，所以46÷2=23”；后一种表达的是“6÷2=3，40÷2=20，20+3=23”，只是“位值”思考与实际数值思考之差别。“标准”的算法也是人为规定的，所以在没学习所谓的课本上“标准算法”之前，让他们陈述自己的想法时，要给予充分的肯定，可以对他们说：“你们真棒！数学家和你们的想法很接近，想看看数学家是怎么计算两位数除以一位数的呢？”再对照学生的算法与小棒图，规范的计算过程的演示，逐步在脑中形成整数除法的定位方则：除到哪一位，商就写在那一位的上面。

学习细节是课堂动态生成的产物，举不胜举，需要执教教师准确把脉，精准针灸，这样才能畅通学生的学习思路，有效共振学生的数学思维。

参考文献：

[1] 陈太春.注意发挥“思维共振”在数学教学中的作用[J].中小学教师培训，2000：（6）.

[2] 何凤波.小学数学思维策略研究[J].教学月刊（小学版）.2012：（4）.

（编辑：胡 璐）