时间序列在安徽省GDP预测中的应用

摘 要：本文搜集了安徽省1978年-2015年的地区生产总值作为数据基础，根据时间序列的相关理论，对数据进行平稳化检验，在通过合理的平稳化处理之后，对数据进行AIC定则检验，找到最合适的模型，并用此模型对参数进行相关估计。这里最终建立的是自回归移动平均模型，经过检验，识别出的最理想模型为ARIMA（1，1，2）。先利用此模型对安徽省2014年和2015年的GDP作出预测，将预测值与实际值进行相对误差分析，得到的相对误差在可控范围之内，从而认为该模型的可行性高。最终利用ARIMA（1，1，2）模型对我省“一三五”规划期间5年地区生产总值做出预测，结果显示超过了2020年的目标GDP。

关键词：ARIMA模型；GDP预测；单位根检验

一、选题的背景及意义

“十二五”已经落下帷幕，总结报告显示这五年我省的地区生产总值从12263.4亿元增长到22005.6亿元，上一个一五相比，总量增加了近1万亿元，这是非常值得欣慰的。现在的安徽已经站上了一个新的发展平台，展望新的一五，我省将继续实施创新、协调、绿色发展，加快创建创文化强省、生态强省、经济强省的步伐，以确保安徽实现全面小康社会。我们将为着这个目标去奋斗，去开创美好安徽的新未来。

本文将以近年来安徽省地区生产总值为基础，建立时间序列模型，对安徽省经济增长的内在特征进行分析。最终使用这个恰当的模型来对安徽省“十三五”期间的地区生产总值做出预测，与“一三五”规划中安徽省2020年的GDP目标值做比较，大致可反映我省是否能达到目标产值的情况。

二、本文主要工作

首先我们从《安徽省统计年鉴》中选取了改革开放以来安徽省1978年-2015年共38年的地区生产总值，对这些基础资料进行对数转化，再求一阶差分或二阶差分，直到相关的序列图和ADF单位根检验通过了平稳性检验。再对平稳化数据进行可能的ARIMA（p，d，q）模型的识别，通过AIC定则筛选出最佳的ARIMA（p，d，q）模型。接着对该模型实施残差序列检验，进一步精确判断模型的准确性。最后用该模型对安徽省进行短期的预测，得到的相对误差在可控范围内即可认为模型的良好，便可以对安徽省“一三五”规划这5年进行地区生产总值预测了。

三、ARIMA模型建模步骤

1.数据的平稳性检验和处理

初始的时间序列数据得到之后，对其平稳性检验必不可少。一般来说，散点图或折线图就可实现，但要做到精确判断还是要依靠ADF单位根检验的相关数值。对非平稳时间序列的处理可以通过取对数、作一阶差分或二阶差分来完成。这里的差分次数就是ARIMA（p，d，q）模型中的阶数d。理论上说，可以通过差分处理来提取非平稳序列中的确定性信息，但并不是一昧的差分阶数越多越好，差分阶数越多，损失的实际数据的信息就越多，所以为避免过度差分，一般将差分次数限制在两次以内。

当数据序列经过平稳化处理之后，我们便可得到相应的d值，这样我们的ARIMA（p，d，q）模型就转化成了ARMA（p，q）模型。

2.模型的定阶

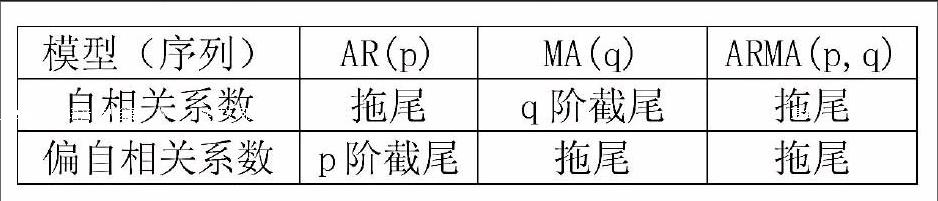
ARMA（p，q）模型的阶数和系数特点我们可以用通过它的相关系数和偏自相关系数初步判定，如下表。

在平稳时间序列中，可以通过自相关和偏自相关系数的分析得到模型的初步阶数，但这并不准确。要想准确的定阶还是通过AIC定则最为靠谱，最终找到一个最理想的模型阶数。

3.参数估计

在数据模型的阶数确定之后，需要来估计ARMA模型的相关设计参数。这里我采用的是OLS最小二乘法。值得我们关注的是：由于MA模型的参数估计比一般模型复杂，当遇到平均移动项含有高阶的ARMA模型或移动平均模型的阶数较高时我们应尽量避免。

4.模型检验

当上面的任务完成以后，需要对模型的估计结果进行诊断和检验，来推断我们所选的模型是否恰当。要想看出拟合的模型合理与否，主要表现在两个方面：首先是模型参数估计值的显著性；其次是模型的残差序列是否符合白噪声序列的条件。

四、基于时间序列的安徽预测分析

安徽省地区生产总值（GDP）受到各方面的经济基础、人文发展、人口增长等诸多因素的影响，这其中存在着各种错综复杂的相关关系。这里我们化繁为简，只将安徽省改革开放以来的三十几年的地区生产总值作为原始时间序列，找出其中的规律，建立理想的数学模型，来预测出我们所需要的未来GDP预测值。这对预测安徽省“一三五”的经济概况具有重要的现实意义。

1.安徽省GDP时间序列分析

在ARMA模型中，时间序列产生于一个平稳的随机过程，若反映在图像上，便是所有的样本点都围绕在某一确定的水平线上下浮动。所以，对非平稳时间序列做好取对数和差分等平稳化处理非常重要。

（1）平稳性检验

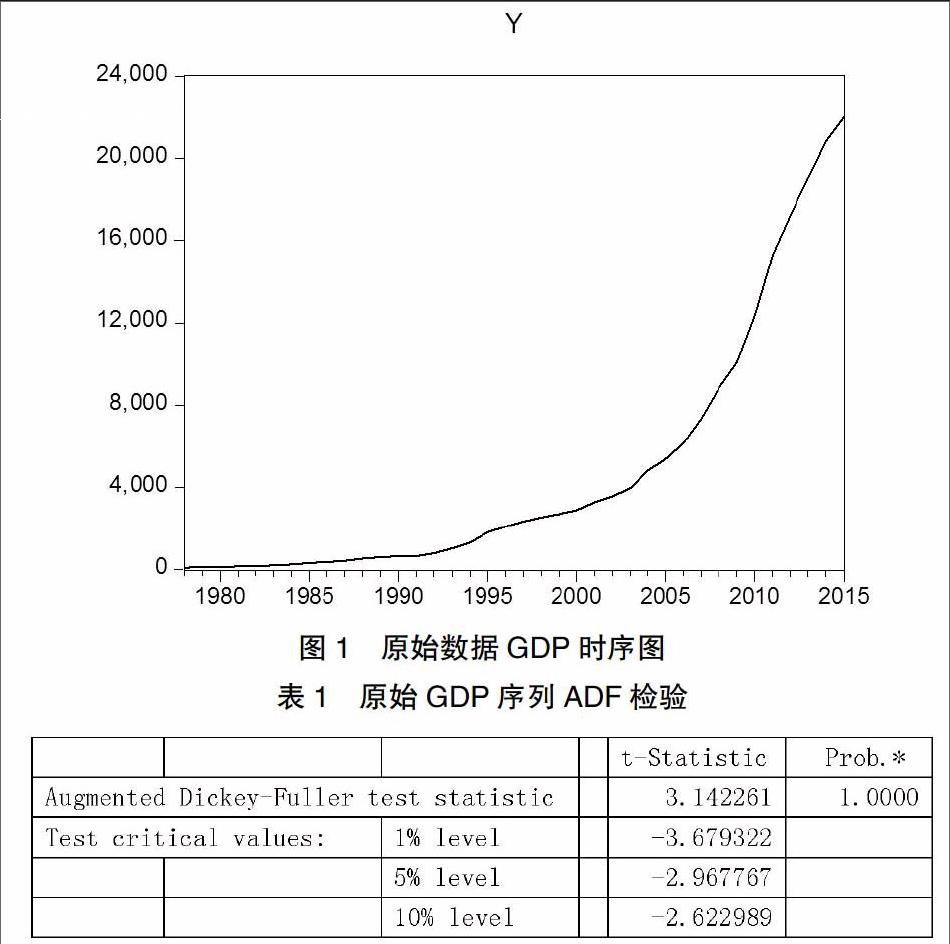
在安徽省原始GDP的时间序列图1中可以看出我省的地区生产总值具有明显呈指数型的上升趋势，所以这个序列明显是非平稳的。进一步进行ADF单位根检验更验证了这个观点，从表1可以看出，p值几乎等于1，t统计量也不乐观。所以检验未通过，表明原始序列是非平稳的。

由于模型的需要，首先要做的就是平稳化处理，这里通常有两种方法，一种是取对数，一种是差分（一阶或二阶），这两种对原序列的平稳化都有显著效果，下面具体介绍。

（2）平稳化处理

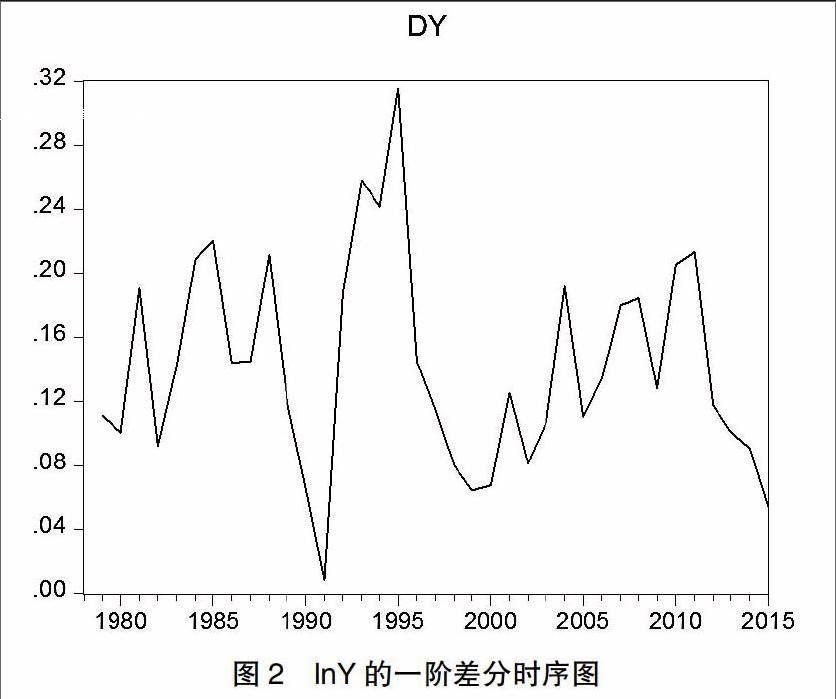
首先对安徽省GDP数据进行对数化处理，记为lnY。在对lnY作图时发现它的上升趋势仍十分明显，且ADF单位根检验中的t统计值分别大于1%，5%，10%水平下的检验值，即序列是非平稳的。所以要进一步进行一阶差分，来提取出这其中曲线趋势的影响。对lnY序列一阶差分后的序列记为DY，它的平稳性检验结果如下：

由图2的时序图可以看出所有的样本点已经基本上在一条水平线上下浮动，但并不直观。于是接下来进行ADF单位根检验，由表2检验结果可以看出，在5%和10%的显著性水平下一阶差分的t统计值均小于相应的Testcriticalvalues，即结论是接受不存在单位根这一说法。并且后面的Prob列读出的p值也比0.05小得多，所以对lnY差分后的序列DY是平稳的。

2.安徽省GDP时间序列模型的建立

本文研究的安徽省GDP是一个一元的时间序列，我们通过对过去的历史数据间的随机误差项构建模型来预测未来所需要的数据。一般来说，随机误差项是在不同时刻都统计独立的，且服从于正态分布。要想找到最合适的ARMA模型，阶数的确定和参数的估计是最重要的因素。

（1）模型的定阶

从样本的自相关与偏自相关函数的图形中可以大致判断序列所要构建的ARMA（p，q）模型的阶数，但想准确确定，还需要一系列的试验。

在图3中，DY序列的自相关系数在滞后一期后出现衰减，并且在后面的滞后阶数中逐渐趋向于零值，这表现出拖尾性；相似的，偏自相关系数在图中也表现为滞后一期后出现衰减并趋于零，但他的偏自相关系数都明显大于0，于是可以大胆的理解为偏自相关系数也具有拖尾性。那么在对模型的阶数进行初步判断时，我们可以取1，也可以取2。准确的定阶我们是通过AIC定则来判断的。

由表3分析可知，在所有可能的ARMA（p，q）模型中，除去未通过检验的模型，剩下的AR（1），ARMA（1，2），MA（1）模型在R-squared、Adjusted R-squared、p值以及DW值的综合判断下拟合效果比较理想。

（2）模型参数估计与建立

分别对上述三种模型进行参数估计，得到的ARMA（1，2）的AdjustedR-squared值比AR（1）和MA（1）的AdjustedR-squared值要大，而且AIC和SC的值前者比后两者要小，故选择ARMA（1，2）最为合适。此处因篇幅有限，只列示出最佳的模型参数估计，如图4：

（3）模型检验

上述工作完成以后，模型的检验也是必不可少的一部分，我们需要检查和诊断统计结果，综合考虑该模型是否符合要求。由ARIMA（1，1，2）模型的残差序列检验图5可以看出，Q统计值均小于对应自由度的的卡方分布的检验值，并且在最后一列我们可以看到所有的p值都显著大于0.05，因此可断定该残差序列是白噪声序列，也可以认为ARIMA（1，1，2）模型通过了检验。

3.安徽省GDP短期预测及分析

在进行预测之前，先用1978年-2013年的安徽省GDP数据对2014年和2015年的GDP作出预测，并与实际值计算得到相对误差，如表4：

由上表可知，2014年-2015年的安徽省GDP预测值与实际值的相对误差都比较小，结合我省的实际情况，该误差算是在可接受的范围内。也进一步说明了ARIMA（1，1，2）模型的可行性和准确性。

最终我们用ARIMA（1，1，2）模型对安徽省未来5年即“一三五”期间的GDP做出预测，预测值如表5所示，轻松突破了我省定下的2020年地区生产总值36000亿元：

五、结术语

本文通过对1978年-2015年安徽省GDP的数据分析及建立的模型，对2016年-2020年安徽省GDP作短期预测，这为安徽省制定经济发展目标提供了决策参考价值。在“一三五”规划大纲中，安徽省的经济发展目标表明，到2020年安徽省地区生产总值目标是36000亿元，并希望能向40000亿元冲刺。从本文的未来5年的预测值看出，2020年预测可达到37112.87亿元的GDP，超过了一三五规划中安徽的GDP目标。

参考文献：

[1]安徽省一三五规划纲要.安徽省发展和改革委员会.

[2]王黎明，王连，杨楠.应用时间序列分析[M].上海：复旦大学出版社，2009.

[3]李守丽.时间序列模型在地级市GDP预测中的应用[J].郑州大学，2013（5）.

[4]王燕.应用时间序列分析[M].中国人民人学出版社，2005：1-239.

[5]张晓彤.Eviews使用指南与案例[M].北京：机械工业出版社，2007：78-89.

作者简介：宋静（1995- ），女，安徽六安人，安徽财经大学，应用统计学专业